
| << Previous [1] 2 3 4 5 ...6 Next >> |
The Cosmic Tetractys
The 2nd-order tetractys

In Sacred geometry/Tree of Life, we discussed various methods of transforming examples of sacred geometry in order to decode the scientific and spiritual information that they embody. The next level of decoding sacred geometry after the Pythagorean tetractys is through its next-higher version — the 2nd-order tetractys, in which each of the 10 yods of the tetractys is replaced by another tetractys. This generates 85 yods, which is the sum of the first four integer powers of 4:
85 = 40 + 41 + 42 + 43.
The yod at the centre of the 2nd-order tetractys denotes Malkuth of the central tetractys, which itself corresponds to this Sephirah. It is surrounded by 84 yods. The 2nd-order tetractys therefore expresses the fact that 84 Sephirothic degrees of freedom in a holistic system exist above Malkuth — its physical form. Of these, (7×7 − 1 = 48*) degrees are pure differentiations of Sephiroth of Construction symbolized by coloured, hexagonal yods in the seven 1st-order tetractyses that are not at the corners of the 2nd-order tetractys. The remaining 36 degrees are denoted by both the 15 white yods at the corners of the 10 tetractyses (these yods formally symbolize the Supernal Triad) and the 21 coloured, hexagonal yods that belong to the tetractyses at the three corners of the 2nd-order tetractys and which, therefore, also refer to the Supernal Triad of Kether, Chokmah & Binah. YAH (יה), the older version of the Godname YAHWEH (יהוה) assigned to Chokmah, has the number value 15 and prescribes the 15 corners of the 10 1st-order tetractyses. ELOHA (אלה), the Godname of Geburah with number value 36, prescribes both the 36 yods lining the sides of the 2nd-order tetractys and the 36 yods just discussed. The number 84 is the sum of the squares of the first four odd integers:
84 = 12 + 32 + 52 + 72.
As
n2 = 1 + 3 + 5 + ....+ 2n–1,
where n is any positive integer, n2 is the sum of the first n odd integers, so that 84 is the sum of (1+3+5+7=16=42) odd integers:
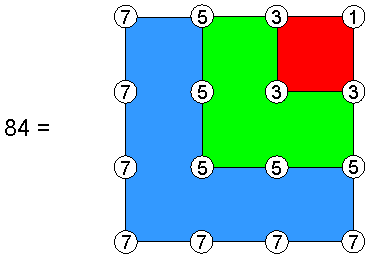
The Tetrad determines the number of yods surrounding the centre of a 2nd-order tetractys. These yods include 15 corners of 1st-order tetractyses, where
15 = 20 + 21 + 22 + 23 = 1 + 2 + 4 + 8
(the number value of YAH) is the sum of the first four integer powers of 2. There are (85–15=70) hexagonal yods, where 70 = 10×7 = (1+2+3+4)×fourth odd/prime number. These two properties illustrate again how the Tetrad determines properties of the next higher-order tetractys above the 1st-order tetractys. In mathematics, triangular numbers (1, 3, 6, etc) can be represented by triangular arrays of dots and tetrahedral numbers (1, 4, 10, etc) can be represented as a tetrahedral pile of these arrays. The piles representing tetrahedral numbers can themselves be piled up into 4-dimensional "tetrahedral numbers": 1, 5, 15, 35, 70, etc. The fourth, non-trivial example of these numbers is 70. This is the number of hexagonal yods in the 2nd-order tetractys. Once again, the Tetrad determines both a class of number and a specific member of this class that is a parameter, or measure, of the Pythagorean representation of Wholeness. It is an example of how the Tetrad Principle governs the mathematical nature of holistic patterns and systems (for more details, see Article 1).
As another illustration of this principle, the four integers 1, 2, 4 & 8 are the first four terms in the geometric series:
1, 2, 4, 8, 16, 32, ....
in which each term is twice the previous one. They appear in what is known as Plato's Lambda. In his treatise on cosmology called "Timaeus," Plato has the Demiurge marking a strip of the substance of the World Soul into sections measured in length by the numbers 1, 2, 4 & 8 on one side of it and the numbers 31 (=3), 32 (=9) & 33 (=27) on its other side (see here). The number of corners of the 10 1st-order tetractyses in the 2nd-order tetractys is
15 = 20 + 21 + 22 + 23 = 1 + 2 + 4 + 8,
whilst the number of yods in the 2nd-order tetractys is
85 = 12 + 22 + 42 + 82.
The number of yods surrounding its centre is
84 = 22 + 42 + 82,
and the number of hexagonal yods is
85 − 15 = 70 = (22 − 2) + (42 − 4) + (82 − 8).
This illustrates the power of the integers 2, 4 & 8 to generate properties of the 2nd-order tetractys. In mathematics, there are only four orders of normed division algebras**: the 1-dimensional scalar numbers, the 2-dimensional complex numbers, the 4-dimensional quaternions and the 8-dimensional octonions. Such is its archetypal power as the arithmetic counterpart of sacred geometries, the Lambda and its complete, tetrahedral generalisation (see here) generate not only the tone ratios of the notes of the Pythagorean musical scale (see here) but also the dimensions of the four types of algebras permitting division! The four integers 1, 2, 4 & 8 spaced along the first raised edge of this tetrahedron:
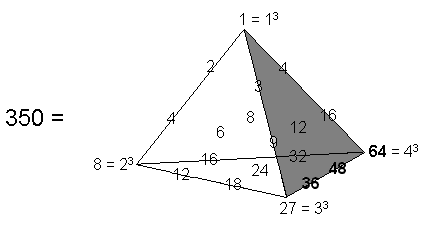 |
The Tetrahedral Lambda is the generalisation of Plato's Lambda, which served as the basis of his cosmology. |
generate as their sum the 15 corners of the 10 1st-order tetractyses in the 2nd-order tetractys, whilst the four integers 1 (=40), 4 (=41), 16 (=42) & 64 (=43) spaced along its third raised edge generate as their sum its 85 yods:
1 + 4 + 16 + 64 = 85.
We see that the first raised edge of the tetrahedral array of 20 integers, which we call the Tetrahedral Lambda in the section Plato's Lambda, generates the number 15 measuring the "skeleton" of the 2nd-order tetractys in terms of a basic, triangular array of 15 points, namely, the corners of 10 1st-order tetractyses. Its third raised edge generates the complete "body" of the 2nd-order tetractys comprising 85 yods. This illustrates the character of the number 15 of YAH, the Godname of Chokmah, as the fifth triangular number.
The sum of the seven integers on the first and third raised edges of the Tetrahedral Lambda = 1 + 2 + 4 + 8 + 4 + 16 + 64 = 99. As the sum of all its 20 integers is 350, the sum of the remaining 13 integers is 251. This is the number of yods in the 1-tree when its 19 triangles are Type A (see here). It is embodied in the UPA as the number of space-time coordinates of points on the 10 whorls as 10 closed curves in 26-dimensional space-time: 10×25 + 1 = 251. Notice that the sum of the squares of the four integers on the first raised edge:
12 + 22 + 42 + 82 = 85
is the same as the sum of the four integers on the third raised edge:
1 + 4 + 42 + 43 = 85.
This means that the number 168 which, being a parameter of holistic systems, always displays the division 168 = 84 + 84 (see here), can be expressed as:
22 + 42 + 82 + 41 + 42 + 43.
The holistic parameter 336 = 2×168, which is discussed in numerous places on this website, can be expressed as 4×84 = 42 + 43 + 44. As 336 = 350 − 14, where 14 is the sum of the integers 2, 4 & 8 on the first raised edge, we see that the sum of the squares of these three integers is 84, which is the sum of the nine integers on the boundary of the first face of the Tetrahedral Lambda, whilst the sum of all its integers except 2, 4 & 8 is 336, which is 4×84, i.e., the sum of the integers 4 assigned to all the 84 yods surrounding the centre of a 2nd-order tetractys.
The correspondences between the 2nd-order tetractys, the 1-tree and the Sri Yantra are discussed here.
* Numbers in boldface are the number values of either the Hebrew names of the Sephiroth or their manifestation in the four Worlds of Atziluth, Beriah, Yetzirah & Assiyah (see here).
** See here for a definition of normed division algebras.
| << Previous [1] 2 3 4 5 ...6 Next >> |