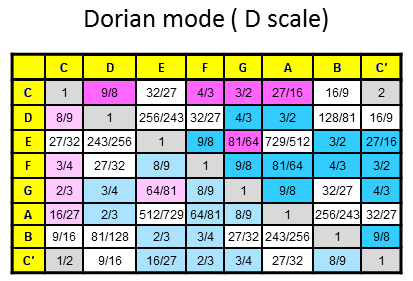
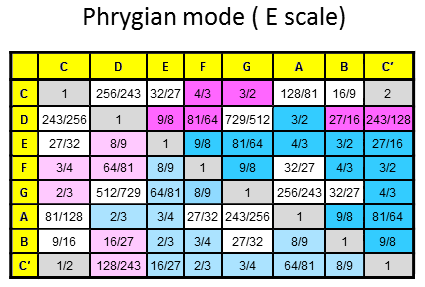
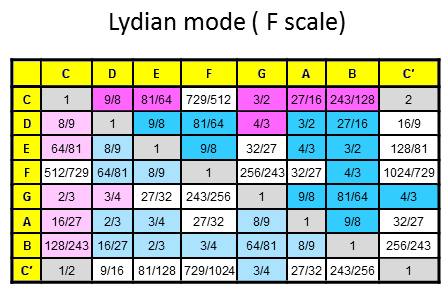
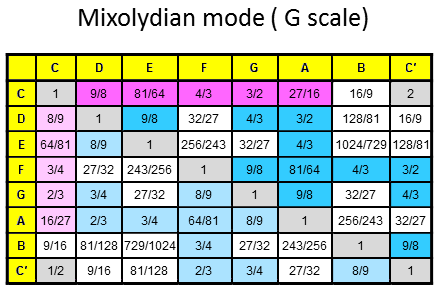
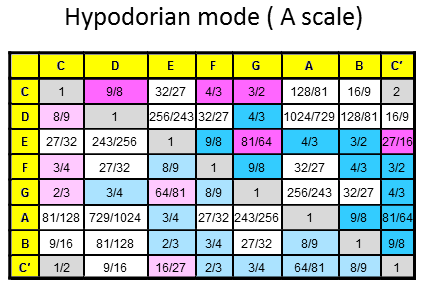
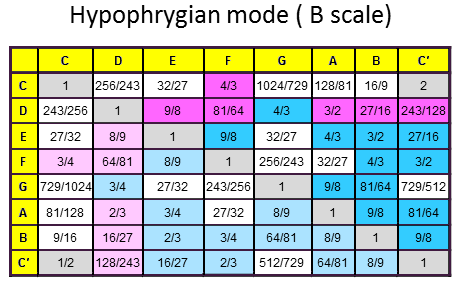
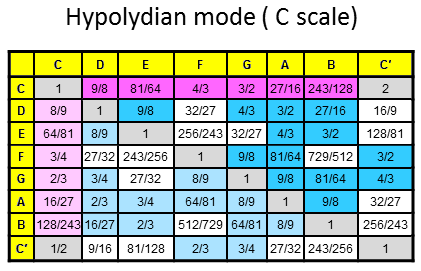
The 84 repeated, Pythagorean intervals between the notes in the seven diatonic scales

Tabulated below are the numbers of rising intervals (Pythagorean/C scale & non-Pythagorean) between the eight notes C-C′ in each of the seven diatonic scales:

Comments

• The seven diatonic scales have 66 non-Pythagorean intervals (indicated by white cells) below the octave between their (7×8=56) notes (42 notes between the tonic and octave). 66 is the 65th integer after 1, showing how ADONAI, the Godname of Malkuth with number value 65, prescribes the seven scales.
• The seven scales have 123 rising, Pythagorean intervals (dark red & dark blue cells), of which 26 are their note intervals, leaving 97 other intervals, where 97 is the number of Haniel, the Archangel of Netzach, the seventh Sephirah from the top of the Tree of Life, and 26 is the number value of YAHWEH, the Godname of Chokmah. The number 123 is the 10th Lucas number: 123 = L₁₀ = Φ¹⁰ + Φ⁻¹⁰, where Φ is the well-known Golden Ratio: Φ = 1.6180.... Amazingly, this number is also the average number of points, lines & triangles needed to construct half a Platonic solid from Type A polygons (see Fig. 22 & p. 22 here). The number of rising & falling Pythagorean intervals = 2×123 = 246. This is the number value of Gabriel, the Archangel of Yesod. It is the average number of points, lines & triangles required to construct a whole Platonic solid. As holistic systems, the seven diatonic scales and the five Platonic solids embody the same global parameters. Here is a striking example of this shared property.
• Of the 123 Pythagorean intervals, 84 are repetitions of the minimum number of different Pythagorean intervals occurring in each scale, totalling 39 for all seven scales. This means that there are 84 repetitions of rising, Pythagorean intervals (dark blue cells) and 84 repetitions of falling, Pythagorean intervals (light blue cells), i.e., there are 168 repeated, rising and falling, Pythagorean intervals. This number is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth.
• The four Authentic Modes (Dorian, Phrygian, Lydian & Mixolydian) have 48 repetitions of rising, Pythagorean intervals, where 48 is the number value of Kokab, the Mundane Chakra of Hod, whilst the three Plagal Modes (Hypodorian, Hypophrygian & Hypolydian) have 36 such repetitions, where 36 is the number of ELOHA, the Godname of Geburah. This 48:36 division differentiates between Authentic and Plagal Modes and is a characteristic feature of sacred geometries, where it divides the geometry into two significant parts. For example:

1. The lowest Tree of Life with its 19 triangles turned into tetractyses has 48 yods up to Chesed, the first Sephirah of Construction, and 36 more yods up to its top, including four yods outside it;
2. The 2nd-order tetractys, the Pythagorean representation of holistic systems, has 84 yods surrounding its centre, of which 48 hexagonal yods belong to the seven 1st-order tetractyses that express the seven Sephiroth of Construction, leaving 36 yods (15 corners of the 10 1st-order tetractyses & 21 hexagonal yods in the 1st-order tetractyses at the three corners of the 2nd-order tetractys):

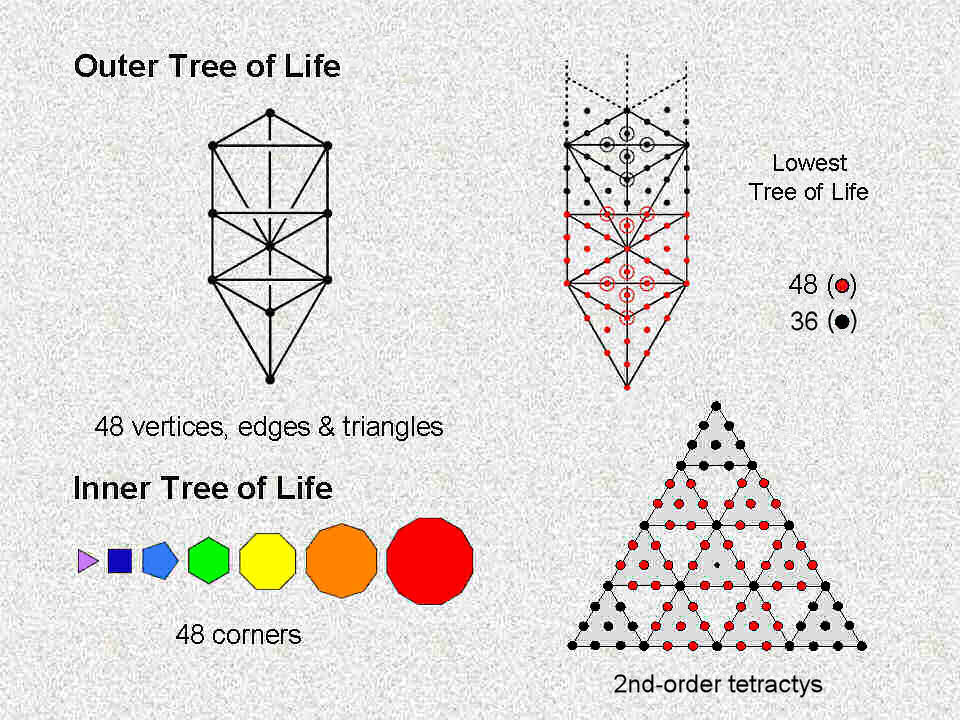
Alternatively, 36 yods line the boundary of the 2nd-order tetractys, inside which are 48 yods surrounding its centre.
3. The inner Tree of Life consist of seven regular polygons with 48 corners, the first six of which have 36 corners. The musical counterpart of the metaphysical demarcation between the "objective" section of the Tree of Life, whose commencement is marked by Chesed, the first Sephirah of Construction, and the "subjective" domain above this point is the distinction between the four Authentic Modes and their plagal counterparts — or, more precisely, the three types of diatonic scales that pair with them, the Hypomixolydian Mode (the plagal counterpart of the Dorian Mode) being identical to the latter as a diatonic scale.

4. The third and fourth layers of the 3-dimensional Sri Yantra contain 24 triangles with 48 corners; they correspond to the 48 repeated, Pythagorean intervals in the four Authentic Modes:

Circles divided into two semicircles with different colours denote corners of triangles in adjacent layers, one corner being directly above the other.

The first and second layers contain 18 triangles with 36 corners; they correspond to the 36 repeated, Pythagorean intervals in the three Plagal Modes. The Sri Yantra expresses the holistic pattern of 84 repeated, Pythagorean intervals in the seven diatonic scales, at the same time distinguishing between the Authentic and Plagal Modes.

• In terms of notes, the 84 repeated, Pythagorean intervals consist of five types:

The Pythagorean interval 243/128 for note B in the C and F scales is absent form the set of 84 intervals because it is the only type of interval that never appears more than once in a mode (Phrygian, Lydian, Hypophrygian & Mixolydian). There are (28+11=39) repetitions of notes D and E and (23+17+5=45) repetitions of notes F, G & A. Hence, the 168 rising & falling, repeated, Pythagorean intervals comprise (2×39=78) rising and falling D & E intervals and (2×45=90) rising and falling F, G & A intervals. Remarkably, this reproduces the respective gematria number values 78 and 90 of Cholem and Yesodoth in the Kabbalistic name of the Mundane Chakra of Malkuth:

Alternatively, there are 78 rising and falling repetitions of intervals E, F & A and 90 rising and falling repetitions of intervals D & G.

• The 84:84 division in the holistic parameter 168 appears musically in the seven diatonic scales in terms of 84 rising Pythagorean intervals and 84 falling Pythagorean intervals. It manifests in the UPA (the subquark state of the E₈×E₈ heterotic superstring remote viewed by Annie Besant and C.W. Leadbeater with the yogic siddhi called "anima") as the distinction between the outer half of each of its helical whorls, composed of 840 circular turns, and its inner half, similarly comprising 840 turns (see here). As each whorl makes five revolutions about the axis of spin of the UPA, it comprises 168 turns in each half-revolution, that is, 84 turns in each quarter-revolution:

Both the vibrating whorl and the seven diatonic scales represent mathematically complete cycles that embody the same holistic/universal pattern described in The holistic pattern. Article 64 analyses how sacred geometries embody this 84:84 division.

• Another characteristic division of the holistic parameter 168 is 56:56:56. The ways in which it manifests in sacred geometries are discussed here. The D interval is repeated 28 times, the E & G intervals appear (11+17=28) times and the F & A intervals appear (23+5=28) times. Therefore, the 168 repetitions of rising and falling, Pythagorean intervals are composed of 56 D intervals, 56 E & G intervals and 56 F & A intervals. This set of numbers, too, has a superstring counterpart in the root composition of E₈, which has 240 non-zero roots, 168 of which do not belong to its exceptional subgroup E₆ and form three sets of 56 8-tuples:

3×56 roots of E8 that are not roots of E6	3×56 sets of repeated, Pythagorean intervals between notes in 7 diatonic scales
	56 rising and falling D intervals 56 rising and falling E & G intervals 56 rising and falling F & A intervals

Notice that there are 168 8-dimensional root vectors of E₈ that have just two of their eight components (integral or half-integral) that are either the same or of opposite signs. It is not merely that the oscillations of the E₈×E₈ heterotic superstring are loosely analogous to the specific vibrations of sound that constitute the 42 notes between the tonic and octave of the seven diatonic scales and their intervals, although the former are circularly polarised vibrations, not longitudinal waves like sound waves. What is revealed here is far more significant than that! Rather, it is that musical and superstring vibrations are both expressions of the same mathematical pattern that is embodied in sacred geometries (see The holistic pattern and here). The implications of the existence of this fundamental isomorphism are profound ..... .

<< Previous    1...   41  42  [43]  44  45    Next >>

Home