| << Previous 1... 70 71 [72] 73 74 ...81 Next >> |
#72 The 687 yods in the 7 enfolded Type B polygons denote the 687 permutations of the rows of yods in the 7 enfolded Type A polygons
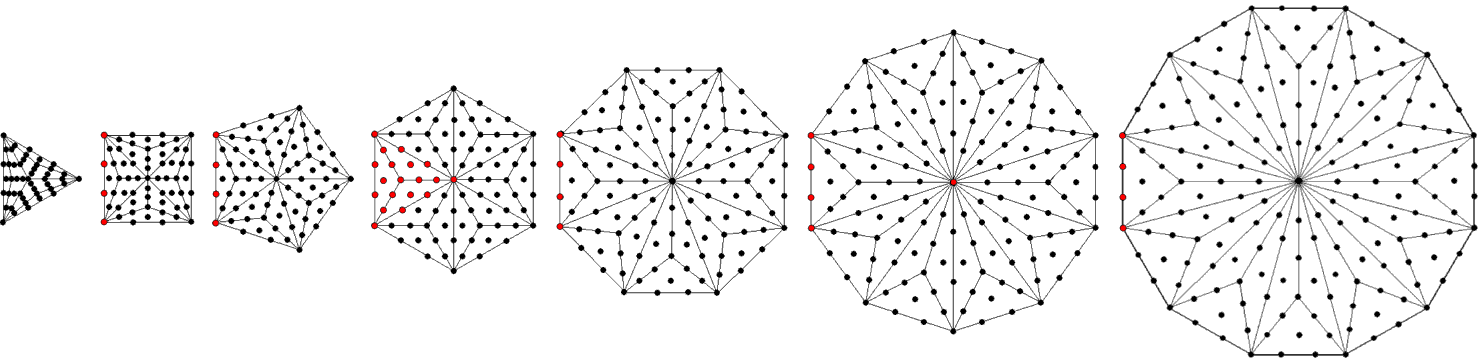
A Type B n-gon has (15n+1) yods (see here). The number of yods in the 7 separate Type B polygons of the inner Tree of Life with 48 corners = ∑ (15n+1) = 15×48 + 7 = 727. This is the 129th prime number, showing how YAHWEH SABAOTH, the Godname of Netzach with number value 129, prescribes the yod population of the 7 separate Type B polygons. When they become enfolded, all their left-hand sides coincide, so that (6×4=24) yods in these sides disappear. Together with 16 other yods that disappear when the 7 polygons become enfolded, they are colored red in the diagram below:

As the triangle becomes a sector of the hexagon, the 15 red yods in this sector outside its left-hand side disappear. As the tip of the pentagon becomes the centre of the decagon, the latter is also coloured red. The number of yods in the separate polygons that disappear when they become enfolded = 24 + 15 + 1 = 40. The 7 enfolded, Type B polygons have (727−40=687) yods. 680 yods surround their 7 centres (shown as black yods in the diagram below).
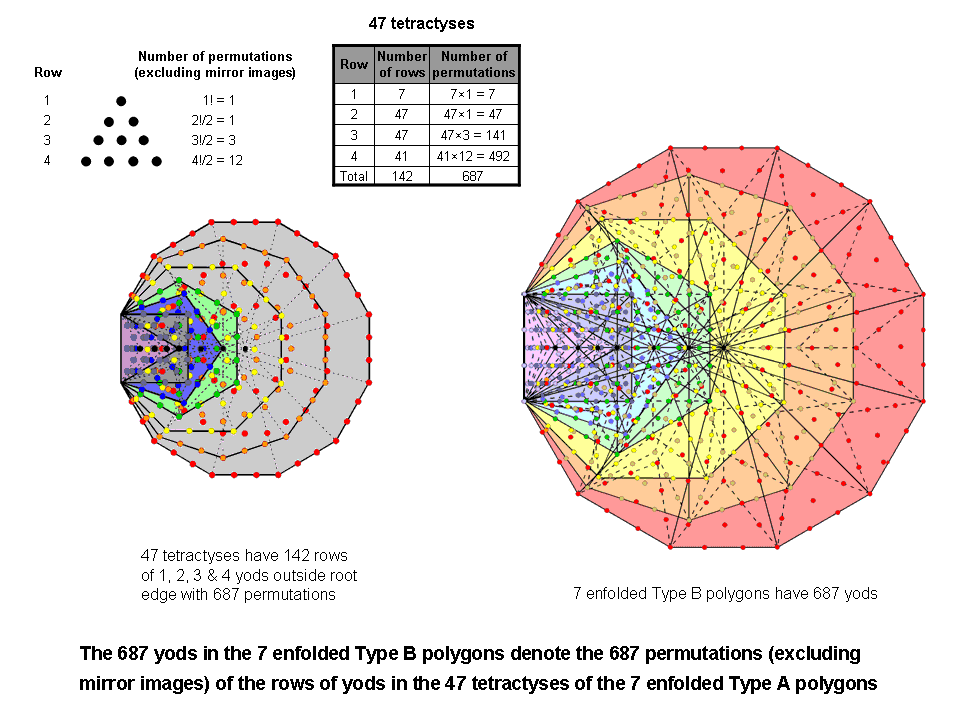
A set of n objects has n! (=1×2×3...×n) permutations. They comprise n!/2 permutations and their n!/2 mirror images, in which the objects appear in reverse order. A set of 4 objects has 12 permutations and their 12 mirror images, a set of 3 objects has 3 permutations and their 3 mirror images, a set of 2 objects has one permutation and its mirror image and one object on its own is its own permutation. Hence, the rows of 2, 3 & 4 yods in a tetractys have 16 (=42) permutations and their 16 mirror images. From now on, we will refer only to a set of permutations that does not include its mirror images, remembering that, apart from the single yod at the apex of a tetractys (row 1), which has only one permutation (namely, itself), every permutation of a row of yods has a different mirror image. All the n tetractyses in a Type A n-gon have its centre as their common apex. There are 12n permutations of the 4 yods on each side, 3n permutations of the n rows of 3 yods, n permutations of the n rows of 2 yods and one permutation of the central yod, i.e., the n-gon possesses (16n+1) permutations of its (3n+1) rows.
Including their centres (coloured black in the diagram opposite and counted as rows of 1 yod), the 7 enfolded Type A polygons with 42 sides have (136+7=143) rows of 1, 2, 3 & 4 yods. The table in the diagram indicates that the 142 rows outside the root edge have 687 permutations of 1, 2, 3 & 4 yods. Of these, 680 permutations are those of (142−7=135) rows of 2, 3 & 4 yods and 7 permutations are just the centres of the 7 polygons, where the tetractys sectors of each polygon meet. Comparing this with the yod composition of the 7 enfolded Type B polygons shown opposite, we see that their number of yods (687) is identical to the number of permutations of the 142 rows of 1, 2, 3 & 4 yods outside the root edge of these polygons when they are Type A. The number of yods (680) surrounding their 7 centres, each regarded as a row of one yod, is equal to the number of permutations of the 135 rows of 2, 3 & 4 yods outside the root edge. This is an amazing property of the inner Tree of Life. The permutational potential of the rows of yods in its 7 enfolded Type A polygons is encoded in the yod population of its 7 enfolded Type B polygons! That the number 687 is a parameter of all holistic systems is confirmed by the fact that the 43 Type A triangles of the 2-d Sri Yantra contain 687 yods surrounding its centre that are not corners of these triangles (see here).
As the number of mirror reflections of the permutations of rows of 2, 3 & 4 yods equals the number of the latter in the 7 enfolded Type B polygons, there are 680 such mirror reflections, so that, altogether, there are 1360 such permutations, where
| 10 | 20 | 30 | 40 | |
| 1360 = | 50 | 60 | 70 | 80 |
| 90 | 100 | 110 | 120 | |
| 130 | 140 | 150 | 160 . |
Amazingly, this is the sum of the gematria number values of Malkuth, ADONAI (its Godname), Sandalphon (its Archangel), Ashim (its Order of Angels), and Cholem Yesodoth (its Mundane Chakra):
496 + 65 + 280 + 351 + 168 = 1360.
It is also the number of corners & triangles that surround the centres of the 5 Platonic solids when their faces are divided into their sectors and the internal triangles created by joining vertices and face centres to the centre of the solid are Type A (see here). 680 corners & triangles in each half of the 5 Platonic solids surround their centres. The (7+7) enfolded Type B polygons have 1370 yods (see here). There are enough yods to symbolise the 1367 permutations of the 142 rows of 1, 2, 3 & 4 yods outside the root edge. However, as 7 is an odd integer, the 7 centres cannot be represented symmetrically by equal numbers of yods in each set of 7 enfolded polygons. Nor can either set of 680 permutations be symbolised by yods that include those on the root edge, as the latter are shared by both sets of polygons. This would indicate that, when both permutations and their mirror images are considered, what should be associated with each set are just 680 of the 683 yods outside the root edge in each set of 7 polygons. Three of these yods coincide with the locations of Sephiroth in the outer Tree of Life, so that outside the root edge there are 680 yods in each set (1360 yods in both sets) that do not coincide with Sephiroth of the outer Tree of Life (shown in the picture below as the six black yods that are corners of either the pair of violet triangles or the pair of green hexagons):
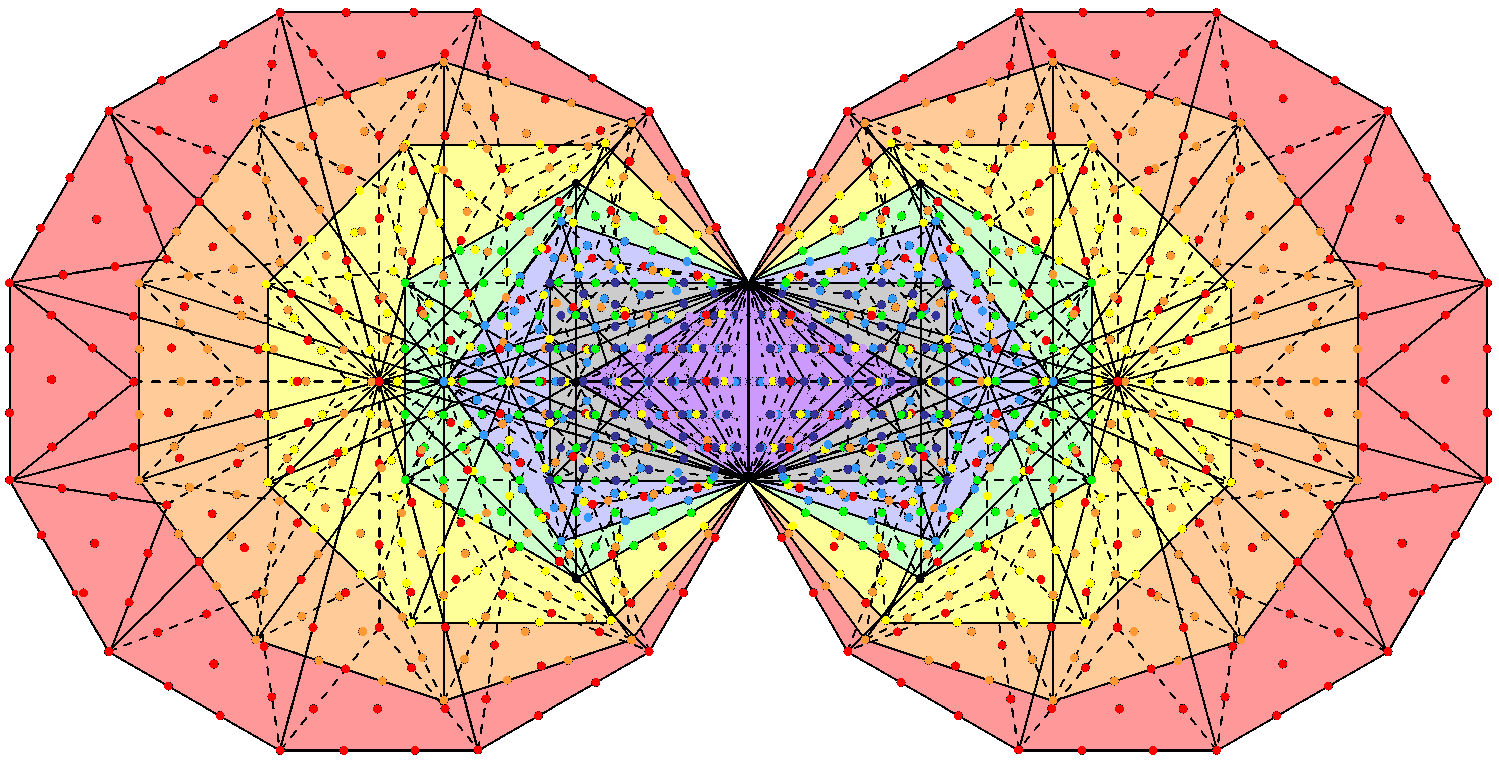
The following correspondences exist between types of yods in the (7+7) enfolded Type B polygons and the types of permutations (mirror reflections included):
|
(7+7) enfolded Type B polygons |
Types of permutations in 47 tetractyses of 7 enfolded Type A polygons |
|
| 1. (47+47=94) sectors have (47+47=94) centres (shared corners of 3 tetractyses in each sector) |
↔ |
47 rows of 2 yods in 47 tetractyses have (47×2!=47+47=94) permutations; |
| 2. (47+47=94) sectors have (47×3 + 47×3 = 282) hexagonal yods at centres of (141+141=282) tetractyses | ↔ | 47 rows of 3 yods in 47 tetractyses have (47×3!=141+141=282) permutations; |
| 3. (47+47=94) sectors have (492+492=984) yods on sides of (141+141=282) tetractyses except those yods in (1) | ↔ | 41 rows of 4 yods outside root edge have (41×4!=492+492=984) permutations; |
| 4. (47+47=94) sectors have (680+680=1360) non-Sephirothic yods in (141+141=282) tetractyses outside root edge | ↔ | 135 rows of 2, 3 & 4 yods in 47 tetractyses have (680+680=1360) permutations. |
Readers should ask themselves: how plausible is it that all these natural correspondences between the types of yods in the inner Tree of Life and the permutations of their rows could be the result of chance? It is certainly not trivial that each of the 94 sectors of both sets of polygons contains one yod of a certain type, thereby enabling correspondence (1) and three yods of another type, enabling correspondence (2), leaving yods on sides of tetractyses that enable correspondence (3).
Returning to the representation of the 687 permutations by the 687 yods in the 7 enfolded Type B polygons, we found in #41 at Wonders of superstrings that the first four enfolded polygons have 17 tetractyses with 49 rows (including the root edge) of 2, 3 & 4 yods with 248 permutations when their mirror images are excluded (496 permutations, including them — see Article 57). Hence, they have 48 such rows outside the root edge with (248−12=236) permutations. As the 135 rows of 2, 3 & 4 yods in the 7 enfolded Type A polygons outside their root edge have 680 permutations, this means that the last three enfolded polygons have 30 tetractyses with (135−48=87) rows of 2, 3 & 4 yods with (680−236=444) permutations. The number 236 is a parameter of the inner Tree of Life,
|
|
|
|
a. The (70+70) regular polygons enfolded in the 10-tree have 680 intrinsic corners. |
b. The (10+10) dodecagons enfolded in the 10-tree have (680+680) yods outside their root edges surrounding their centres. |
being the number of yods that line the 83 sides of the (7+7) enfolded Type A polygons (see here). So, too, is the number 444, which is the number of hexagonal yods in their (47+47) tetractyses (see here). The number 680 is prescribed by YAH, the Godname of Chokmah with number value 15, because:
680 = 12 + 32 + 52 + 72 + 92 + 112 + 132 + 152.
As 680 = 85×8,
85 = (12+32+52+72+92+112+132+15 2)/8,
i.e., the yod population of the 2nd-order tetractys is the arithmetic mean of the squares of the first eight odd integers up to 15. As
1 + 2 + 3 +...+ 15 = 120 = 8×15,
8 = (1+2+3+...+15)/15,
i.e., the number 8 is the arithmetic mean of the first 15 integers, so that
85 = 15×(12+32+52+72+92+112+132+ 152)/(1+2+3+...+15).
This shows how the number value 15 of YAH expresses the yod population of the 2nd-order tetractys. The (7+7) enfolded Type A polygons have 70 corners (see #1). Of these, the topmost corners of the two hexagons coincide with the lowest corners of the two hexagons belonging to the (7+7) polygons enfolded in the next higher Tree of Life. This means that 68 corners are intrinsic to the 14 enfolded polygons, so that the number of corners of the 14n polygons enfolded in the n-tree ≡ N(n) = 68n + 2, where "2" denotes the topmost corners of the two hexagons enfolded in the nth Tree that coincide with the lowest corners of the two hexagons enfolded in the (n+1)th Tree. Therefore, N(10) = 682, i.e., the 140 polygons enfolded in the 10-tree have 680 corners that are intrinsic to them (see diagram a above). This number quantifies the shape of the inner Tree of Life counterpart of the 10-tree. It manifests in the inner form of a single Tree of Life as the 680 permutations of the 135 rows of 2, 3 & 4 yods outside the root edge in the 47 tetractyses that make up the 7 enfolded Type A polygons. As the Type A dodecagon contains 73 yods, 68 yods outside the side that it shares with its mirror image in the inner Tree of Life surround its centre. Therefore, (680+680) yods outside the 10 root edges surround the centres of the 20 dodecagons that are enfolded in the 10-tree (see diagram b above). These yods symbolise the 680 permutations and their mirror images. As the expanded, Tree of Life representation of the 10 Sephiroth, the 10-tree is complete, so that it should come as no surprise that the number 680 quantifying a property of its inner form should be a parameter of other holistic systems, such as the five Platonic solids discussed earlier, for they, too, mathematically speaking, represent the complete set of convex, regular polyhedra.
As pointed out previously, the n tetractyses in a Type A n-gon have (3n+1) rows with (16n+1) permutations (that is, (32n+1) permutations, when the mirror images of the 16n permutations are included). The Type A dodecagon (n=12) is composed of 12 tetractyses having 36 rows of 2, 3 & 4 yods with (16×12=192) permutations and their 192 mirror images. This 192:192 division of the 384 permutations is characteristic of holistic systems (see here and here). Its presence in the last of the regular polygons making up the inner Tree of Life is yet more confirmation of the holistic character of this polygon, whose properties are analysed here. Including its centre formally as a single permutation, the (36+1) rows of the 73 yods in a Type A dodecagon — the tenth type of regular polygon — have (384+1=385) permutations, where
|
12 |
||||
| 22 | 32 | |||
| 385 = |
42 |
52 |
62 |
|
| 72 | 82 | 92 | 102 . |
This illustrates the beauty and power of the Decad in expressing properties of holistic systems. The dodecagon has 35 rows of 2, 3 & 4 yods outside the shared root edge with (192−12=180) permutations. As the 135 rows of 2, 3 & 4 yods outside the root edge in the 7 enfolded polygons have 680 permutations, this means that the first 6 enfolded polygons ending with the 10-sided decagon have (135−35=100=102) such rows with (680−180=500=50×10) permutations, i.e., 1000 (=103) permutations when their 500 mirror images are included. This further illustrates the power of the Decad, for Article 4 demonstrates that this subset of polygons constitutes a holistic system in its own right (just as the dodecagon does) because it embodies the parameters and patterns that define and characterise such systems.
According to the table in the main diagram, the 47 rows of 3 yods in the 7 enfolded Type A polygons have 141 permutations, each row having 3 permutations (and, of course, their 3 mirror images). This is the number of hexagonal yods at the centres of the (47×3=141) tetractyses that make up the 7 enfolded Type B polygons. There remain 539 permutations of either 2 or 4 yods that correspond to the (680−141=539) yods surrounding the centres of the 7 enfolded Type B polygons and lining the sides of their 141 tetractyses. The number 539 is the sum of the Godname numbers of the 7 Sephiroth of Construction:
31 + 36 + 76 + 129 + 153 + 49 + 65 = 539.
It is remarkable testimony to the deep harmony of sacred number and sacred geometry that the 539:141 division of yods in the 7 enfolded Type B polygons into those either lining tetractyses or at their centres corresponds to the division of permutations into 539 permutations of rows of 2 or 4 yods and 141 permutations of rows of 3 yods.
| << Previous 1... 70 71 [72] 73 74 ...81 Next >> |