#73 Correspondence between the 2nd-order tetractys and the 1-tree

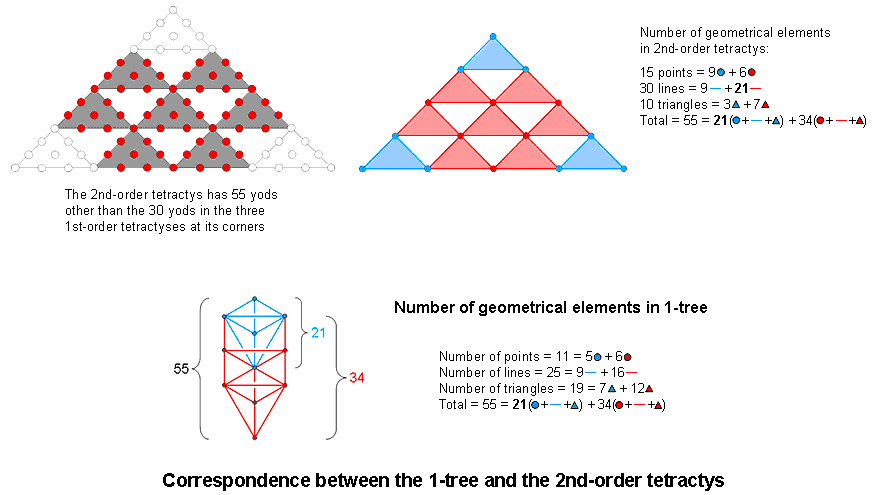
The 2nd-order tetractys comprises 85 yods, where

85 = 4⁰ + 4¹ + 4² + 4³.

The three 1st-order tetractyses at its corners representing the Supernal Triad contain 30 yods, where

30 = 1² + 2² + 3² + 4²,

so that the seven 1st-order tetractyses representing the seven Sephiroth of Construction have (85−30=55) red yods, where

55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

is both the tenth triangular number and the tenth Fibonacci number in the Fibonacci sequence:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 223, ...

This is also the number of points, lines & triangles in the 2nd-order tetractys (see the diagram above), showing how this Pythagorean representation of holistic systems embodies the number 55. Moreover, as each triangle is composed of three corners, three sides & one triangle, i.e., seven geometrical elements, the blue triangles at the corners of the 2nd-order tetractys comprise 21 geometrical elements, leaving 34 geometrical elements making up the seven red triangles, i.e., 55 = 21 + 34. The number 21 is the eighth Fibonacci number and 34 is the ninth Fibonacci number. The 1-tree is composed of 11 corners and 25 sides of 19 triangles, i.e., 55 geometrical elements. Its Upper Face (the blue kite shape with Kether, Chokmah, Binah, Daath & Tiphareth at its corners) comprises five blue points, nine blue lines & seven blue triangles, i.e., 21 geometrical elements; the remainder of the 1-tree comprises six red points, 16 red sides & 12 red triangles, i.e., 34 geometrical elements. The Upper Face with 21 geometrical elements corresponds to the three blue triangles with 21 geometrical elements at the corners of the 2nd-order tetractys symbolising the Supernal Triad, whilst the rest of the 1-tree with 34 geometrical elements corresponds to the 34 geometrical elements making up the seven red triangles that symbolise the seven Sephiroth of Construction. The appearance of three successive Fibonacci numbers in both the 2nd-order tetractys and the 1-tree is the manifestation of a deeper connection between this type of number and the geometry of the n-tree because the number of geometrical elements in the latter is

N(n) = 34n + 21,*

where the kite shape formed by Tiphareth, Netzach, Hod, Yesod & Malkuth has 21 geometrical elements, so that N(n+1) − N(n) = 34, i.e., 34 more geometrical elements appear in successively overlapping Trees of Life. In particular, the 2-tree has (55+34=89) points, lines & triangles, where 89 is the 11th Fibonacci number. The 34:21 division reflects in the 2nd-order tetractys the distinction between the three blue triangles at its corners and the seven red triangles, i.e., between the Supernal Triad and the seven Sephiroth of Construction. Many sunflowers have their florets arranged in 55 spirals, 34 of which are clockwise and 21 are anticlockwise:

The florets in this sunflower lie on 34 clockwise spirals and 21 anticlockwise spirals.

Article 50 (Part 1) and Article 50 (Part 2) discuss how Fibonacci numbers shape other sacred geometries. #8 at Sacred geometry/Sri Yantra discusses how the 3-dimensional Sri Yantra embodies the Fibonacci numbers up to 89.

* Proof: the n-tree has (12n+7) triangles with (6n+5) corners and (16n+9) sides. Number of corners, sides & triangles in the n-tree = (6+16+12=34)n + (5+9+7=21).

<< Previous    1...   71  72  [73]  74  75  ...81    Next >>

Home