#54 Correspondence between the combined Trees of Life and the hexagon, heptagon & octagon

Octagon
When the sectors of an n-sided n-gon are 2nd-order tetractyses, it contains (72n+1) yods, where 72 is the number value of Chesed. Of these, 62n are hexagonal yods, where 62 is the number value of Tzadkiel, the Archangel of this Sephirah. The number of yods surrounding the centre of an octagon = 8×72 = 576 = 24² = 1²×2²×3²×4². They include (8×62=496) hexagonal yods and 80 corners of 80 1st-order tetractyses, where 496 is the number of Malkuth, the last Sephirah, and 80 is the number of Yesod, the penultimate Sephirah.

Combined Trees of Life
The outer Tree of Life with its 16 triangles turned into tetractyses contains 70 yods. Of these, 60 green yods are hexagonal yods. The inner Tree of Life with tetractyses as the 94 sectors of its (7+7) enfolded polygons contains 444 hexagonal yods (they are coloured according to the colour of their corresponding polygon). Four pairs of white hexagonal yods on the two vertical, internal sides of the sectors of the two hexagons are shared with four tetractyses of the outer Tree. When it is superposed onto the plane of the 14 polygons, the number of hexagonal yods in the combined Trees = 60 − 4×2 + 444 = 496. This is the number of hexagonal yods in an octagon with 2nd-order tetractyses as its sectors. With 1st-order tetractyses as its sectors, the octagon contains 49 yods. 49 is the number of EL ChAI, the Godname of Yesod. The Godname therefore prescribes the dimension 496 of the two symmetry groups E₈×E₈ and SO(32) at the heart of superstring theory.

Heptagon
The number of yods surrounding the centre of a heptagon with 2nd-order tetractyses as its sectors = 7×72 = 504. They include (7×62=434) hexagonal yods (shown in the diagram as either coloured or white) and 70 black corners of 70 1st-order tetractyses.

Combined Trees of Life
Of the 444 hexagonal yods in the inner Tree of Life, two lie on the root edge and eight coloured white are shared with the outer Tree. The number of hexagonal yods outside the root edge of the (7+7) enfolded polygons that are intrinsic to them because they are not shared = 444 − 2 − 8 = 434. This is the number of hexagonal yods in the heptagon.

Each sector of an n-gon adds 62 hexagonal yods to its hexagonal yod population when it is a 2nd-order tetractys. The 8-gon has 62 more hexagonal yods than a 7-gon because it has one more sector. Their counterparts in the combined outer & inner Trees of Life are the extra two yods on the root edge of the (7+7) enfolded polygons and the 60 hexagonal yods in the outer Tree of Life: 434 + 2 + 60 = 496.

The 496 hexagonal yods in the combined Trees of Life are also discussed in #30 of Wonders of sacred geometry/Superstrings and in Article 54. 

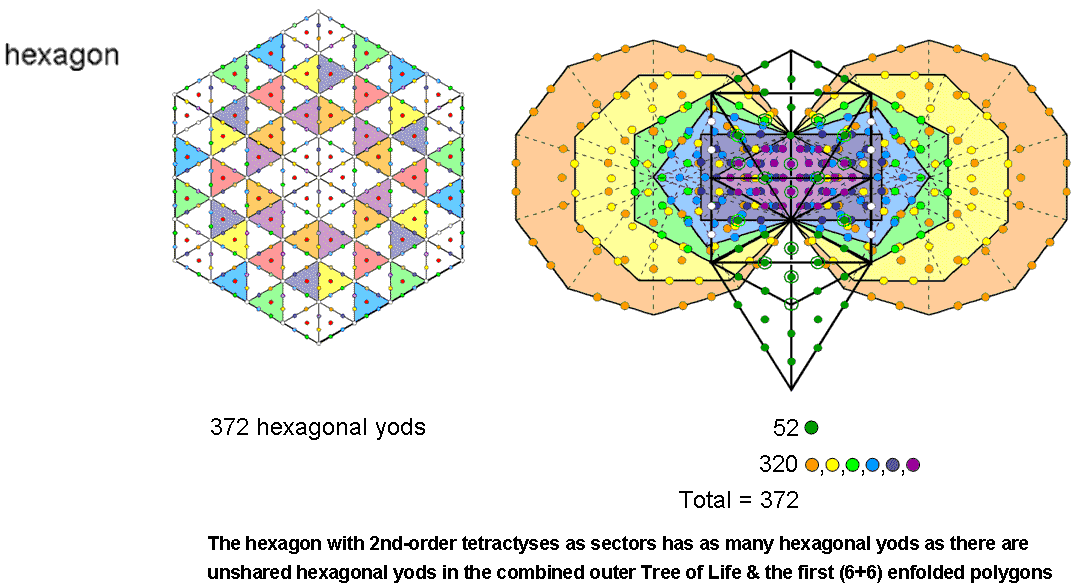
Hexagon
The number of hexagonal yods in a hexagon with 2nd-order tetractyses as its sectors = 6×62 = 372.

Combined Trees of Life
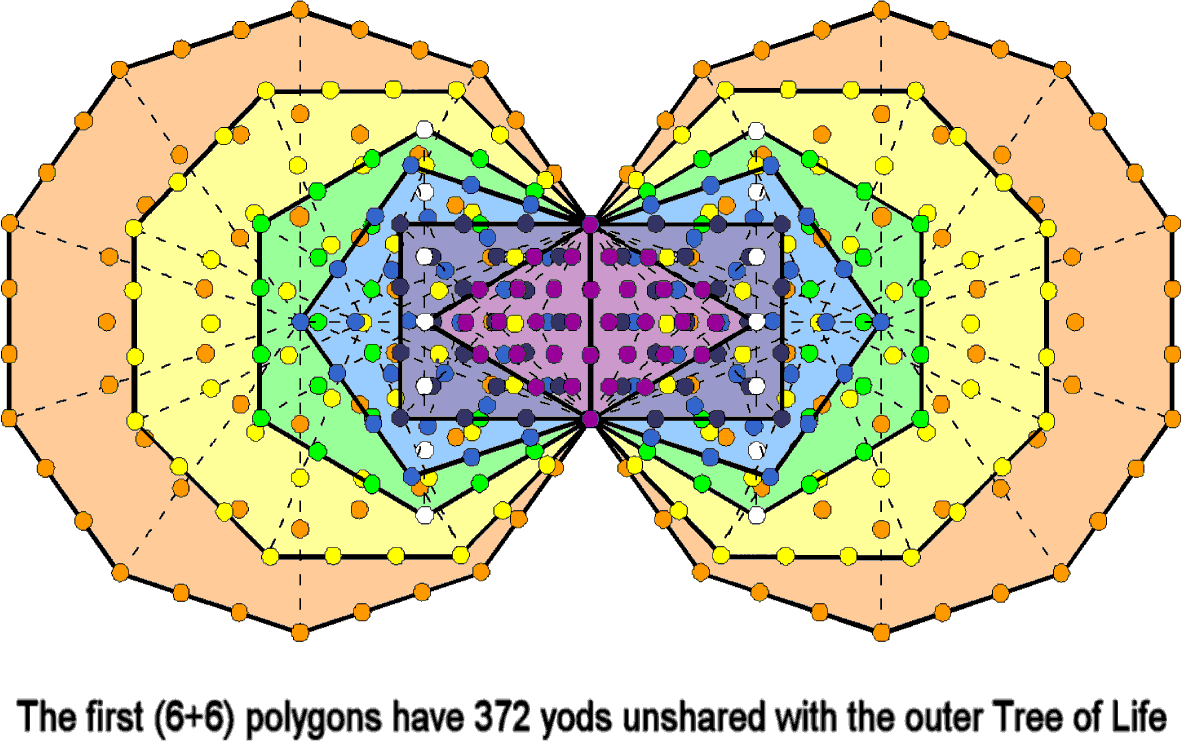
A dodecagon has 60 hexagonal yods (58 outside the root edge). The (7+7) enfolded polygons have 444 hexagonal yods. The number of hexagonal yods in the first (6+6) enfolded polygons = 444 − 2×58 = 328. Eight of these (shown in the diagram opposite as white yods) are shared with the outer Tree of Life. The first (6+6) enfolded polygons have (328−8=320) hexagonal yods that it does not share with the outer Tree. The latter has (60−8=52) hexagonal yods that it does not share with the inner Tree of Life. The combined Trees of Life have (52+320=372) unshared hexagonal yods. This is the number of hexagonal yods in the hexagon with 2nd-order tetractyses as sectors. We see that, whereas the octagon embodies the number of hexagonal yods in the combined Trees of Life and the heptagon embodies the number of unshared hexagonal yods outside the root edge of the (7+7) enfolded polygons, the hexagon embodies the number of hexagonal yods in the combined outer Tree & the first (6+6) enfolded polygons. This is remarkable.

The (7+7) enfolded polygons have 524 yods. The dodecagon has 69 yods outside the root edge. The number of yods in the first (6+6) enfolded polygons = 524 − 2×69 = 386. Of these, seven yods lie on each side pillar of the outer Tree. The number of unshared yods in the first (6+6) enfolded polygons = 386 − 7 − 7 = 372. This is the number of unshared hexagonal yods in the combined outer Tree & the first (6+6) enfolded polygons.

Clearly, the number 372 embodied in a single hexagon is a characteristic parameter of both the first (6+6) enfolded polygons and their combination with the outer Tree of Life. This is because this set of polygons constitutes a holistic system in itself (for example, see Article 4 for how the Godnames of the 10 Sephiroth prescribe it). What is remarkable is that the transformation of single polygons by the 2nd-order tetractys reveals numbers that quantify the properties of such systems. The fact that the properties are related discredits the suggestion that their embodiment in these polygons is a matter of coincidence. This is confirmed by the discussion here of the decagon with 2nd-order tetractyses as its sectors. It has 620 hexagonal yods, which is the number of hexagonal yods outside the root edge of the combined outer Tree with Type A triangles and the inner Tree with Type A polygons — another property that is analogous to those analyzed above.

 

<< Previous    1...   52  53  [54]  55  56  ...81    Next >>

Home