| << Previous 1... 28 29 [30] 31 32 ...56 Next >> |
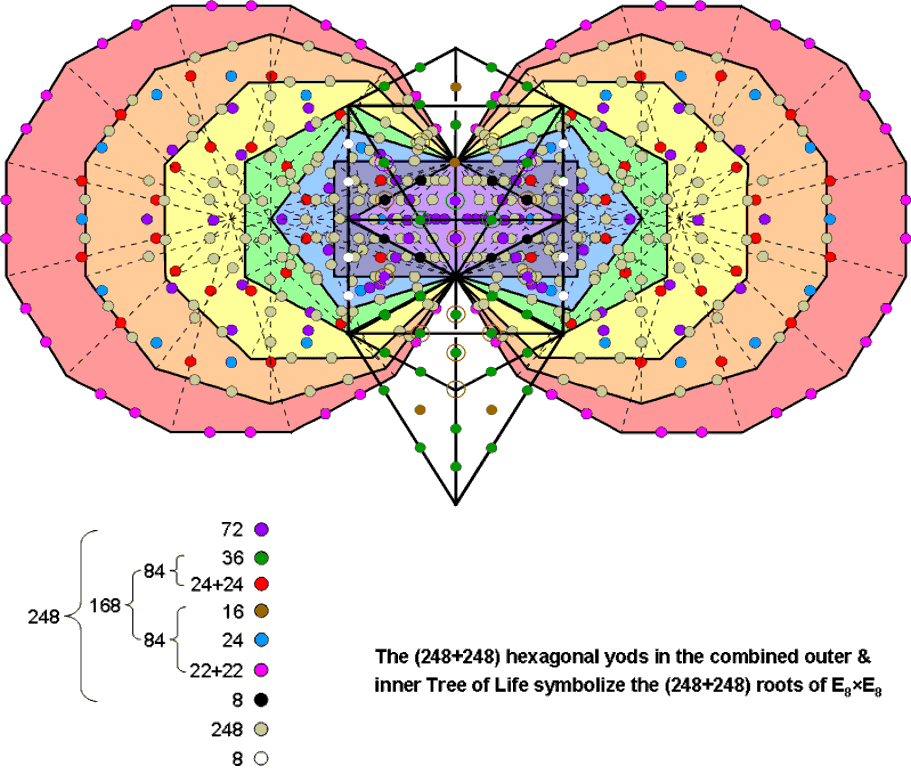
#30 The counterpart of the root composition of E8×E8 in the yod composition of the combined outer & inner Trees of Life

Outer Tree of Life
Turned into tetractyses, the 16 triangles contain 60 hexagonal yods consisting of the 16 brown hexagonal yods at
their centres and the 44 hexagonal yods on their 22 sides (see diagram above). As four of these sides are sides of
the sectors of the two hexagons belonging to the inner Tree of Life, the outer Tree of Life has (22−4=18) sides
with (18×2= 36) green hexagonal yods that are unshared with its inner form as hexagonal yods, as
well as (4×2=8) white hexagonal yods that are shared. Hence, the outer Tree has (16+36=52)
unshared hexagonal yods. 52 is the 26th even integer, showing how YAHWEH with number value
26 determines the population of hexagonal yods that are intrinsic to the outer Tree. The two
hexagonal yods on the Chesed-Geburah Path are the centres of the two violet triangles belonging to the (7+7)
enfolded polygons, so that they are corners of tetractyses belonging to the latter. This means that
50 of the 52 hexagonal yods intrinsic to the outer Tree are hexagonal yods from the
perspective of both Trees, showing how ELOHIM, the Godname of Binah with number value
50, prescribes this property.
Inner Tree of Life
Turned into tetractyses, the (47+47=94) sectors of the (7+7) enfolded polygons have 524 yods. They consist of
80 corners of 94 tetractyses and 444 hexagonal yods, where 80 is the
number of Yesod. The latter comprise 94 hexagonal yods at the centres of tetractyses and (444−94=350) hexagonal
yods that line their sides. Each dodecagon has 48 hexagonal yods lining sides of tetractyses.
The 46 such yods outside the root edge consist of 22 pink hexagonal yods on its sides and 24 red hexagonal yods on
internal sides of its 12 tetractyses. Hence, 46 = 22 + 24 and 350 = 46 + 2 + 46 + 256, where "2" denotes the two
purple hexagonal yods on the root edge, there being 256 (=44) hexagonal yods outside it that line
tetractyses in the first (6+6) enfolded polygons. Each set of the first six enfolded polygons has 35 sectors; the
dodecagon has 12 sectors. (35+35=70) of the 94 hexagonal yods at centres of tetractyses belong to the first (6+6)
enfolded polygons; they are coloured purple. The 24 remaining hexagonal yods belong to the two dodecagons; they are
coloured blue. Therefore,
444 = 350 + 94
= 46 + 2 + 46 + 256 + 70 + 24
= 22 + 24 + 2 + 22 + 24 + 256 + 70 + 24
= (70+2) + 24 + 22 + 24 + 22 + 24 + 256.
Combined outer & inner Trees of Life
When the outer and inner Trees are combined, the eight white hexagonal yods on the two side pillars of the former
coincide with some of the hexagonal yods in the two hexagons that belong to the latter. It was found above that
there are 52 hexagonal yods in the outer Tree that are unshared as such with the inner Tree. The number of
hexagonal yods in the combined Trees = 52 + 444 = 496. This is the dimension of both
E8×E8 & SO(32), the two symmetry groups that govern the anomaly-free interactions
between heterotic superstrings. This property constitutes amazing evidence for the Tree of Life basis of
superstring theory because, although it might be coincidental, only the most extreme debunker would
be willing to consider this a plausible possibility, especially given the additional properties of this number
embodied by the combined Trees of Life to be discussed next.
Collecting together the various results discussed above:
496 = 52 + 444 = (16+36) + (70+2) + 24 + 22 + 24 + 22 + 24 + 256.
The 256 hexagonal yods lining tetractyses in the first (6+6) enfolded polygons comprise eight black hexagonal yods on the four sides of the pair of triangles outside the root edge and 248 khaki hexagonal yods (let us write this set as 248′). Therefore,
496 = (16+36) + (70+2) + 24 + 22 + 24 + 22 + 24 + 8 + 248′ = 248 + 248′,
where
| 248 |
= (16+36) + (70+2) + 24 + 22 + 24 + 22 + 24 + 8 = 8 + (70+2) + (36+24+24) + (16+24+22+22) |
| = 8 + 72 + 84 + 84 = 8 + 72 + 168. |
We find that the hexagonal yod population 496 splits into 248 & 248′. This is analogous to how the dimension 496 of E8×E8′ is the sum of the dimension 248 of E8 and the dimension 248′ of E8′. That the geometry of the combined Trees allows such a natural splitting of this number into two equal numbers is evidence that it is not by chance that they have 496 hexagonal yods. This conclusion is confirmed by the fact that the number 248 further divides naturally into the number 8 denoting the eight simple roots of E8, the number 72 denoting the 72 roots of E6 (an exceptional subgroup of E8) and the number 168 denoting the 168 remaining roots of E8. 168 further divides into two equal numbers 84 (the diagram in #23 shows that the 168 8-tuples group into (56+28=84) 8-tuples and (3×28=84) 8-tuples). This bifurcation is displayed in all the sacred geometries/holistic systems discussed in this website (see here under "168 = 84 + 84"), as is the 72:168 division (see here). Amazing though it may seem, what we are encountering here is not the highly improbable result of miraculous chance but the manifestation of the group mathematics of heterotic E8×E8′ superstring theory in the sublime sacred geometry of the outer & inner Trees of Life.
Let us, next, inspect whence the yod counterparts of the 248 roots of E8 originate:
 |
 |
|
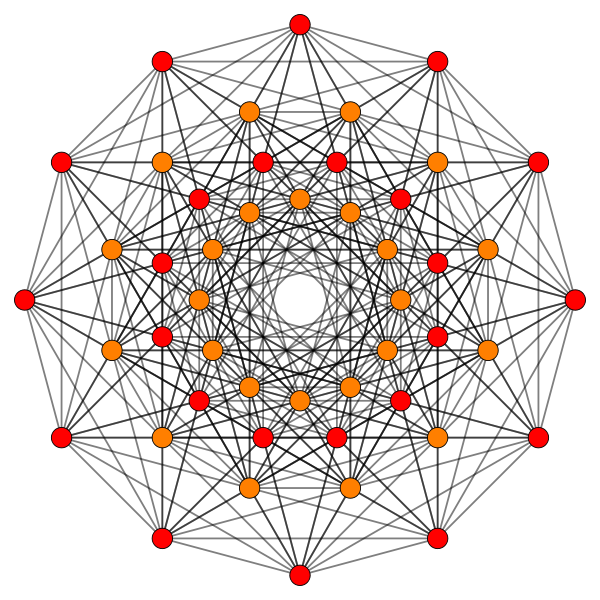
2-d projection of 240 vertices of 421 representing the 240 roots of E8 (see large PDF version here) |
2-d projection of 72 vertices of I22 representing the 72 roots of E6 |
Notice that the 12 polygons embodying the number 72 constitute a holistic subset of the 14 polygons making up the inner Tree of Life, being characterized by the same parameters as those embodied in the complete set. Notice also that the hexagonal yods symbolizing the 168 roots come from the outer Tree (16+36) and from the pair of dodecagons (24+22+24+22+24), which, too, constitute a holistic object. All the hexagonal yods symbolizing the second group E8′ come from the hexagonal yods in the first (6+6) enfolded polygons that surround the hexagonal yods at the centres of the 70 tetractys sectors of these polygons. In terms of the formal correspondence between yods and Sephiroth (see here), such yods correspond to the six Sephiroth of Construction above Malkuth in the outer Tree. Hence, the encoding of E8×E8′ in the combined Trees of Life suggests the following association:
E8 ↔ Malkuth;
E8′ ↔ 6 Sephiroth of Construction above Malkuth.
It would indicate that the symmetry group E8 applies to the forces operating in the familiar, physical universe of ordinary matter, namely, Malkuth, and that E8′ applies to forces operating in a more subtle (although still physical) universe. This is what superstring theorists have called the parallel universe of invisible "shadow matter" that is separated from the ordinary universe by a narrow gap extending along the seventh compactified dimension predicted by supergravity theories. This type of matter is sometimes confused by popular science writers with "mirror matter" — hypothetical particles that are the mirror images of the known subatomic particles. Although shadow matter is similar to this parity-reversed form of matter in not strongly interacting with ordinary matter, it is otherwise completely different, quite apart from being a rigorous, mathematical prediction of E8×E8′ heterotic superstring theory and not just an ad hoc theoretical speculation. The fact that the hexagonal yods symbolizing the roots of E8′ are distributed differently from those denoting the roots of E8 indicates that the break-down of E8′ symmetry proceeds differently from the break-down of E8 symmetry.
The properties of the combined outer & inner Trees of Life are analyzed in depth in Article 54.
| << Previous 1... 28 29 [30] 31 32 ...56 Next >> |