| << Previous 1... 30 31 [32] 33 34 ...56 Next >> |
#32 Yod composition of the Platonic solids

According to the first table in #31 listing formulae for the numbers of its points, lines & triangles surrounding its axis, a regular polyhedron with C vertices, F faces, E edges & n sectors in each face has F corners other than vertices, ( E+nF) sides & nF triangles in its faces that surround its axis passing through two opposite vertices. If each triangle becomes a tetractys, the number of yods other than vertices in its faces that surround its axis = F + 2(E+nF) + nF = F + 2E + 3nF. Including the (C–2) vertices surrounding its axis, the total number of yods = C + F – 2 + 2E + 3nF = 3E + 3nF, where Euler’s formula for a polyhedron:
C – E + F = 2
has been used to replace C by E & F. Noting that ∑E = 90 and ∑nF = 180, the number of yods in their faces surrounding the axes of the five Platonic solids = 3∑(E+nF) = 3(90+180) = 810. Their axes each consist of three yods on either side of its centre. Therefore, (810 + 5×6 = 840) yods in their faces and axes surround the centres of the five Platonic solids, where
840 = 292 – 1 = 3 + 5 + 7 + … + 57
is the sum of the first 28 odd integers after 1. This demonstrates how the second perfect number 28, which is the average number of vertices & edges in the five Platonic solids, determines how many yods surround their centres. The number 840 is a superstring structural parameter, being the number of circular turns in an outer or inner half of a whorl of the UPA/subquark superstring discussed in Occult Chemistry. It is expressed by the Tetrad as
840 = 10×84 = (1+2+3+4)(12 + 32 + 52 + 72).
The centre of a Platonic solid on average is surrounded by (840/5 = 168) yods in its faces & axes. This demonstrates how the superstring structural parameter 168 (the number of circularly polarized oscillations made by a whorl in a half-revolution about the spin axis of the UPA/subquark superstring) is embodied in the five Platonic solids.
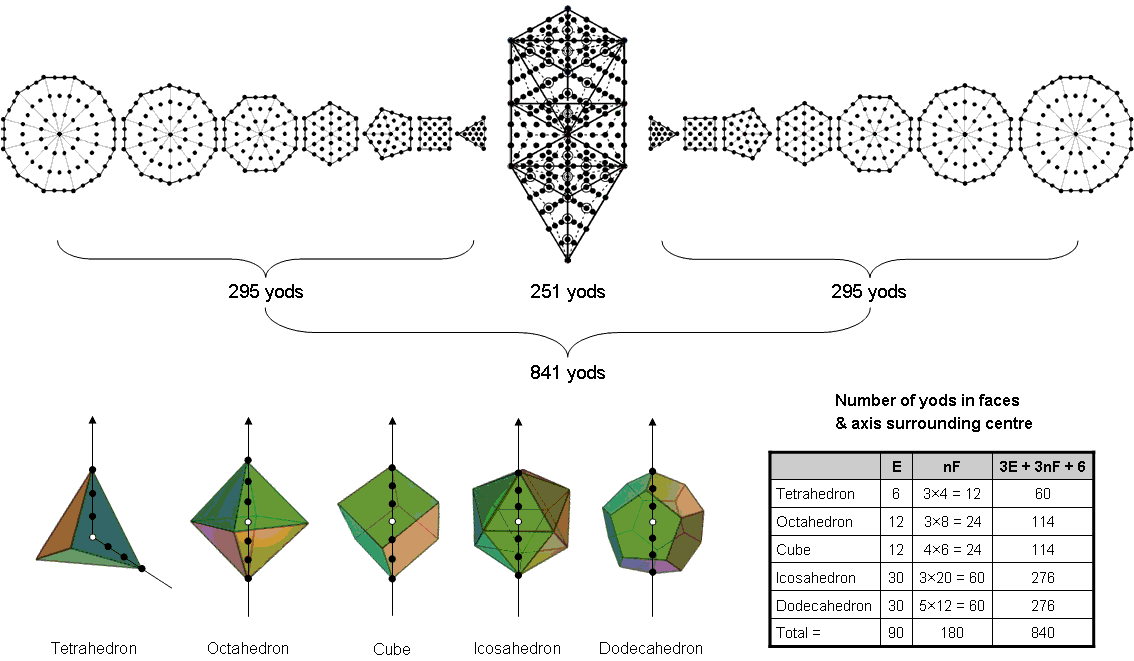
Suppose that the five Platonic solids are nested in one another, occupying the same centre but with their axes pointing in different directions, each axis having three yods on either side of its centre. The number of yods in its faces and on its axis that surround the centre of a Platonic solid = 3E + 3nF + 6. The number of yods in the faces and axes of the five nested Platonic solids, including their shared centre = ∑(3E + 3nF + 6) + 1 = 810 + 5×6 + 1 = 841. The 1-tree with Type A triangles contains 251 yods (see here) and the seven separate Type A polygons contain 295 yods (see here), so that the number of yods in the 1-tree and both sets of seven separate Type A polygons = 251 + 295 + 295 = 841. This demonstrates the Tree of Life nature of the five Platonic solids when they share the same centre.
Surrounding the axes of the five Platonic solids are 40 vertices, 50 centres of faces, 90 edges lined by 180 hexagonal yods and 180 hexagonal yods at centres of the 180 tetractyses in their faces, i.e., (40+50+180+180=450) yods. There are also 360 hexagonal yods lining the 180 sides of these tetractyses that meet at face-centres, whilst lining the axes are 30 black yods that surround the five white centres of the Platonic solids. The 840 yods surrounding the latter is made up of (30+360=390) yods lining either axes or interior sides and 450 yods either lining edges or at centres of tetractyses. On average, (390/5=78) yods are of the former type and (450/5=90) yods are of the latter type. As the graphic at the end of #31 indicates, the average yod populations of the axes and faces of the five Platonic solids reproduce the number value 78 of Cholem and the value 90 of Yesodoth. This is evidence that the number 168 does not appear by chance in this context. It is also embodied in the first four Platonic solids as the average number of yods in their faces and interiors when both are constructed from tetractyses (see here).
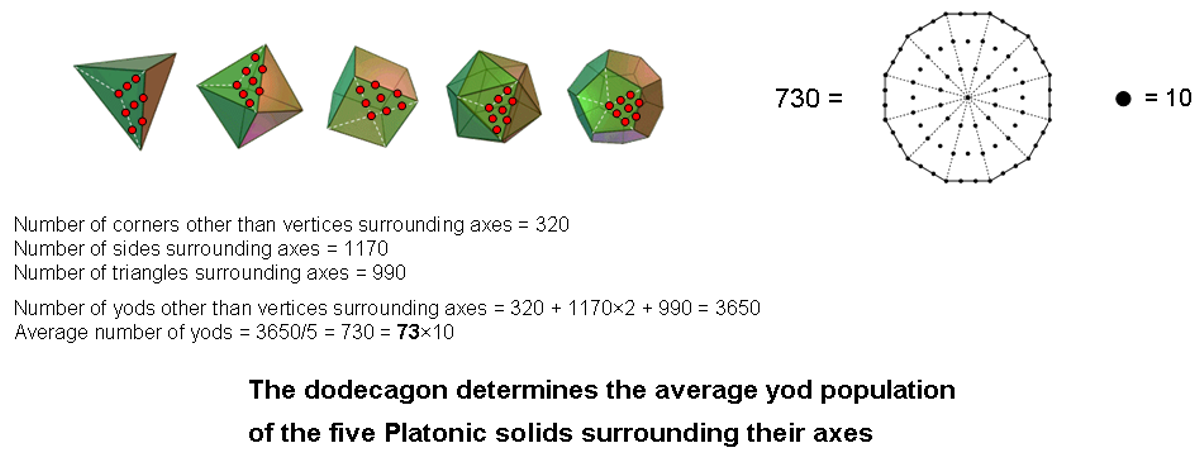
Referring again to this table, surrounding the axis of a regular polyhedron with its edges and sides of face sectors forming internal triangles are (E+F+nF) corners other than vertices, (5E+4nF) sides & (3E+4nF) triangles. Therefore, the total number of yods other than vertices surrounding the axis = E + F + nF + 2(5E+4nF) + 3E + 4nF = 14E + F + 13nF. For the five Platonic solids, this number = ∑(14E + F + 13nF) = 14×90 + 50 + 13×180 = 3650 = 365×10. On average, a Platonic solid has (3650/5=730=73×10) yods other than vertices surrounding its axis (see diagram above). 73 is the gematria number value of Chokmah ("Wisdom"), the second Sephirah of the Tree of Life (see here). When the 40 vertices surrounding their axes are included, there are (3650+40=3690=369×10) yods surrounding their axes, where
369 = 21 + 26 + 50 + 31 + 36 + 76 + 129
is both the sum of the Godname numbers of the first seven Sephiroth and the average number of yods in half a Platonic solid that surround its axis.
According to the first table in #31, the interior of a Platonic solid has (E+nF) corners, (4E+3nF) sides & (3E+3nF) triangles surrounding its axis. The number of internal yods surrounding its axis = E + nF + 2(4E+3nF) + 3E + 3nF = 12E + 10nF. The number of internal yods surrounding the axes of the five Platonic solids = 12×90 + 10×180 = 2880 = 10×288 = (1+2+3+4)(11+22+33+44). On average, the axis of a Platonic solid is surrounded by (2880/5=576) internal yods. This, too, is expressed by the integers 1, 2, 3 & 4 because 576 = 242 = 12×22×32×42. It is a beautiful illustration of how these integers symbolizing the four rows of dots in a tetractys express properties of sacred geometries built from this template. Constructed from tetractyses, the seven enfolded polygons of the inner Tree of Life have 264 yods, of which 144 yods are inside the boundaries of the polygons. The 14 enfolded polygons have 288 internal yods. Hence, the inner form of 10 overlapping Trees of Life consists of 140 polygons with 2880 yods inside them. This is the number of internal yods that surround the axes of the five Platonic solids! Ten Trees of Life are a more differentiated version of a single Tree with its 10 Sephiroth represented by 10 Trees. The appearance of the same number in two sacred geometries that appear, superficially, to be unrelated to each other reveals their equivalence. Other analyses of the inner form of the 10 Trees of Life have shown that they embody archetypal numbers also found in the Platonic solids, such as 1680 (see here). This is because the latter are the regular polyhedral counterpart of the former. It is the real reason why their geometry should be regarded as 'sacred'.