.png)
| << Previous 1... 32 33 [34] 35 36 ...50 Next >> |
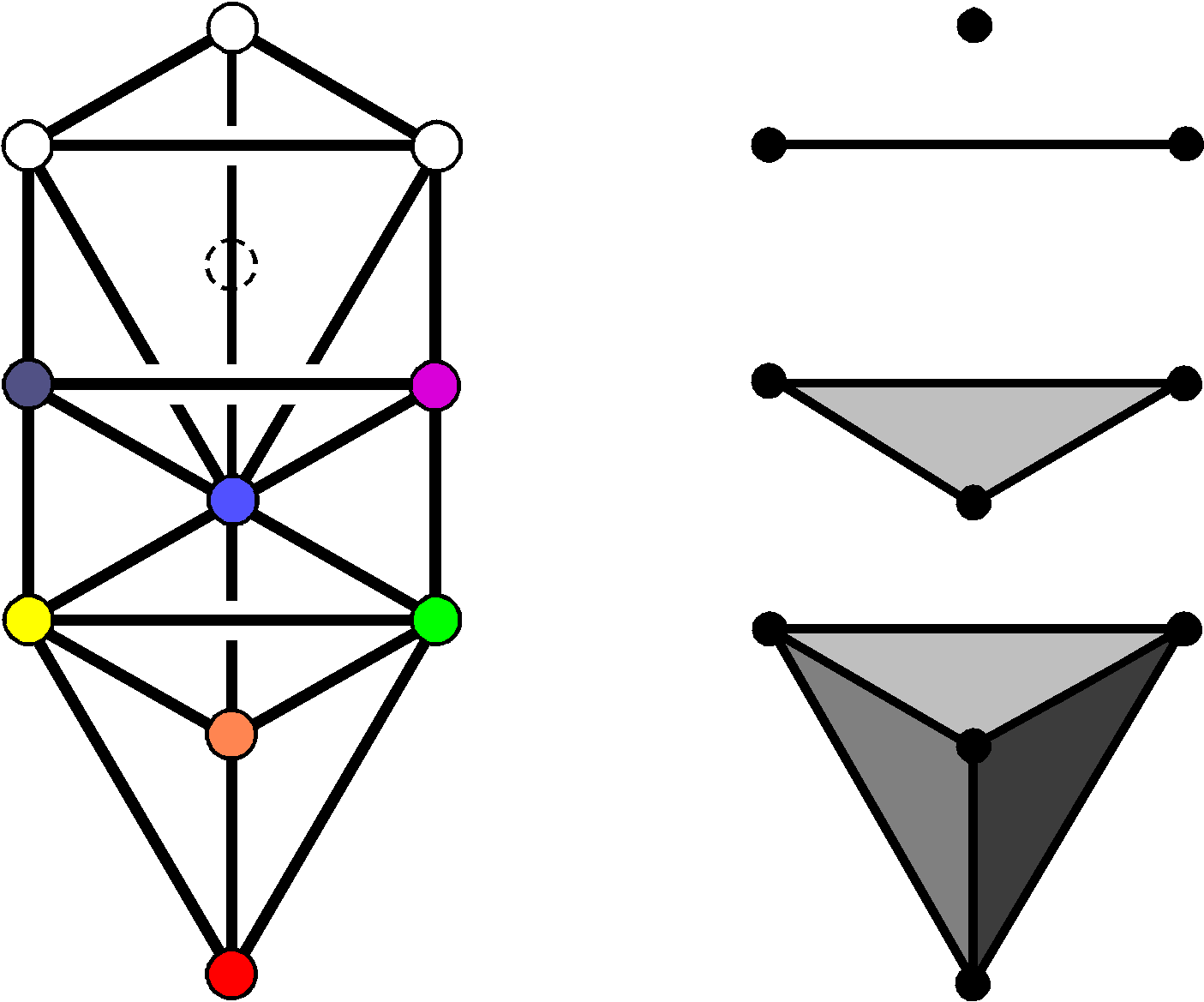
The 10-fold UPA/superstring as the 10-fold division in the 240 yods needed to construct the 1-tree from Type A triangles
.png) |
The 251 yods in the 1-tree. |
When its 19 triangles are turned into Type A triangles, i.e., when each triangle is divided into its three sectors which are then changed into tetractyses, the 1-tree contains 251 yods. The 11 corners of these triangles are “Sephirothic levels” (SLs), as Daath is Yesod of the next higher Tree. Hence, the transformation generates (251−11=240) yods that belong to (19×3=57) tetractyses. The 19 triangles have 25 sides. Inside them are (19×3=57) sides of tetractyses. (251−57=194) yods are on the (25+57=82) sides of these tetractyses, where 194 is the number value of Tzadekh, the Mundane Chakra of Chesed (see Table). The 194 yods comprise (2×82=164) hexagonal yods and (11+19=30) corners. The 1-tree contains (251−30=221) hexagonal yods.
|
|
|
Below the apex of the 1-tree are 248 yods other than SLs. They correspond to the 248 roots of the superstring gauge symmetry group E8 and to the 248 gauge bosons that transmit the unified superstring force. |
The 1-tree is the lowest Tree of a set of overlapping Trees of Life. Below its apex (Kether) and outside the 1-tree on each side are four red hexagonal yods. One is at the centre of a tetractys, two are on a side of this tetractys and another is on the vertical side of another tetractys. These eight hexagonal yods belonging to the next higher Tree of Life consist of two that are at centres of two tetractyses and six that are on four sides of four tetractyses. Below the apex of the 1-tree are therefore eight red, hexagonal yods that belong to the second Tree and 240 black yods other than Sephiroth that belong to the lowest Tree, that is, 248 yods other than Sephiroth, where 248 is the number value of Raziel, the Archangel of Chokmah. The eight red hexagonal yods outside the 1-tree symbolize the eight simple roots of E8, the rank-8, exceptional Lie group with dimension 248; the 240 black yods denote its 240 roots. As the latter include 221 hexagonal yods in the 1-tree, there are (8+221=229) hexagonal yods in the 248 yods that are below the top of the 1-tree. 229 is the 50th prime number, showing how ELOHIM, the Godname of Binah with number value 50, prescribes the number of hexagonal yods below the top of the lowest Tree of Life. As the eight hexagonal yods outside it belong to four tetractyses, the 248 yods belong to (57+4=61) tetractyses, where 61 is the 31st odd integer and 31 is the number value of EL, the Godname of Chesed. They comprise 19 corners, (57+2=59) hexagonal yods at centres of 61 tetractyses & (164+6=170) hexagonal yods on their (82+4=86) sides.
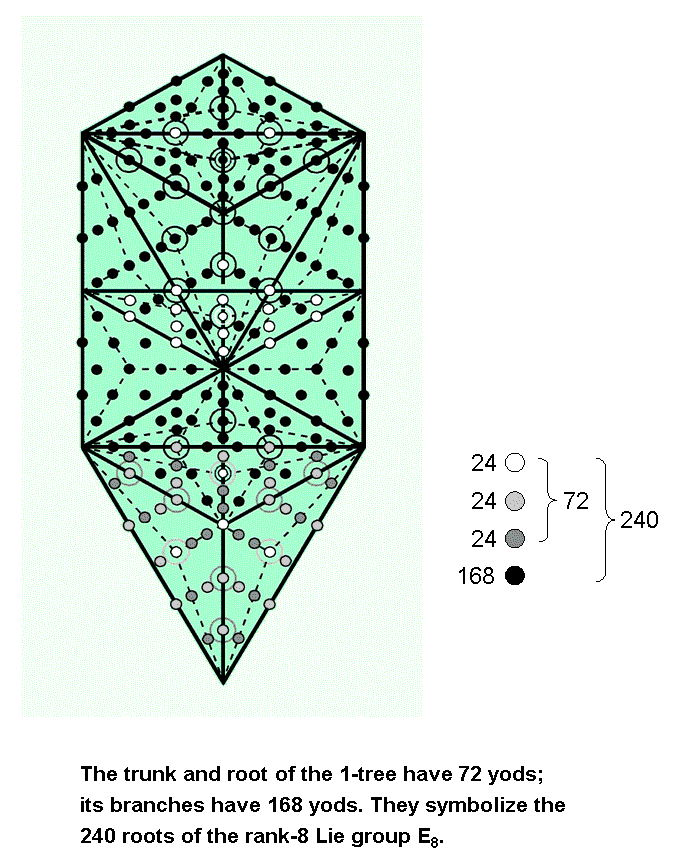
The trunk of the Tree of Life
The trunk of the Tree of Life consists of the mathematical sequence of the point (Kether), straight line (Chokmah-Binah Path), triangle (corners at Chesed, Geburah & Tiphareth) & tetrahedron (vertices at Netzach, Hod, Yesod & Malkuth). It expresses the emergence of 3-dimensional form from the dimensionless point. The ten points in space needed to achieve this represent the integers 1, 2, 3 & 4, which are also symbolized by the four rows of the Pythagorean tetractys. The trunk is composed of 26 geometrical elements (ten points, ten lines, five triangles & one tetrahedron), where 26 is the number value of YAHWEH, the Godname of Chokmah. When these triangles are Type A triangles, the trunk has 15 corners of 15 triangular sectors with 25 sides, i.e., 55 geometrical elements, where 55 is the tenth triangular number:
55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
and the tenth Fibonacci number. This demonstrates how the Decad (10) arithmetically determines the geometrical composition of the trunk of the Tree of Life that embodies this number. The table below lists the numbers of yods in the trunk other than those coinciding with Sephiroth:
The non-Sephirothic yod population of the trunk of the Tree of Life.
| Corners | Hexagonal yods at centres | Hexagonal yods on sides | Total | |
| Point | 0 | 0 | 0 | 0 |
| Line | 0 | 0 | 2 | 2 |
| Triangle | 1 | 3 | 12 | 4 + 12 |
| Tetrahedron | 4 | 12 | 12 + 24 =36 | 4 + (12+12=24) + 24 |
| Total | 5 | 15 | 50 | (2+4+4=10) + 12 + 24 + 24 = 70 |
ADONAI, the Godname of Malkuth with number value 65, prescribes the trunk because its 15 tetractyses have (15+50=65) hexagonal yods. ELOHIM, the Godname of Binah with number value 50, shapes the trunk because 50 hexagonal yods line its 25 sides. The branches of the 1-tree are all those parts of it other than its trunk. They have (240−70=170) yods. As the 240 yods comprise 19 corners of 57 tetractyses & 221 hexagonal yods, the branches contain (19−5=14) corners & (221−65=156) hexagonal yods in (57−15=42) tetractyses, i.e., (14+156=170) yods. The distinction between the trunk & branches of the 1-tree, therefore, generates the division: 240 = 70 + 170, where 70 = 5 corners + 65 hexagonal yods and 170 = 14 corners + 156 hexagonal yods. The 240 yods include (19+57=76) corners & centres of tetractyses, where 76 is the number value of YAHWEH ELOHIM, the Godname of Tiphareth.
According to the table, the numbers of non-Sephirothic yods in the trunk are:
70 = 10 + 12 + 24 + 24.
It has 80 yods if the yods located at the positions of the 10 Sephiroth are included. Suppose that we add the two hexagonal yods on the Path joining Daath and Tiphareth. The projection of this line onto the plane of the (7+7) enfolded polygons making up the inner Tree of Life is the side they all share — what we have called the "root edge." This Path is its counterpart in the outer Tree of Life. It is what may be called the "root" of the Tree of Life. Its trunk and root constitute a set of 72 non-Sephirothic yods, where
72 = (10+2) + 12 + 24 + 24 = (12+12) + 24 + 24 = 24 + 24 + 24.
 The 72 yods consist of three sets of 24 yods (see diagram opposite). This leaves (170-2=168) yods in the branches made up
of 14 corners and 154 hexagonal yods in 14 Type A triangles with two hexagonal yods on each of their 14 sides
(there are actually 15 sides but one side is the line between
Daath & Tiphareth, the two hexagonal yods on which have been added to the 70 yods in the trunk). There are
nine hexagonal yods inside each Type A triangle, so that the 168
yods comprise 14 corners, 14 sets of nine hexagonal yods and 14 pairs of hexagonal yods, i.e., 14 sets of 12
yods, or seven sets of 24 yods. Each set of 24 yods comprises two
centres of triangles of the 1-tree, four hexagonal yods on two Paths and 18 hexagonal yods inside two
triangles. The latter consist of six hexagonal yods at centres of six tetractyses and 12 hexagonal yods on six
sides of them, so that the 24 yods comprise two corners of tetractyses, six hexagonal yods at their centres
and (4+12=16) hexagonal yods on their sides. This 2:6:16 pattern is identical to what is found for the 24
transverse dimensions of bosonic strings, for they comprise two large-scale dimensions, six dimensions of the
compactified space of superstrings and 16 higher dimensions. The following correspondences exist:
The 72 yods consist of three sets of 24 yods (see diagram opposite). This leaves (170-2=168) yods in the branches made up
of 14 corners and 154 hexagonal yods in 14 Type A triangles with two hexagonal yods on each of their 14 sides
(there are actually 15 sides but one side is the line between
Daath & Tiphareth, the two hexagonal yods on which have been added to the 70 yods in the trunk). There are
nine hexagonal yods inside each Type A triangle, so that the 168
yods comprise 14 corners, 14 sets of nine hexagonal yods and 14 pairs of hexagonal yods, i.e., 14 sets of 12
yods, or seven sets of 24 yods. Each set of 24 yods comprises two
centres of triangles of the 1-tree, four hexagonal yods on two Paths and 18 hexagonal yods inside two
triangles. The latter consist of six hexagonal yods at centres of six tetractyses and 12 hexagonal yods on six
sides of them, so that the 24 yods comprise two corners of tetractyses, six hexagonal yods at their centres
and (4+12=16) hexagonal yods on their sides. This 2:6:16 pattern is identical to what is found for the 24
transverse dimensions of bosonic strings, for they comprise two large-scale dimensions, six dimensions of the
compactified space of superstrings and 16 higher dimensions. The following correspondences exist:
This is not coincidental, for the 240 yods symbolize the 240 roots of E8, whose associated gauge charges are spread along the ten whorls of the E8×E8 heterotic superstring, ten to a whorl, and each gauge charge is the result of an oscillation along each of the 24 transverse dimensions of space. Nevertheless, this analogy between the hidden yod composition of the 1-tree and the pattern of dimensions of space predicted by the theories of bosonic strings and superstrings is remarkable.
Notice that the 72 yods, which symbolize the 72 roots of E6, the rank-6, exceptional subgroup of E8, have been compounded from a set of 70 yods making up the trunk of the 1-tree and the two hexagonal yods of the Daath-Tiphareth Path. The diagram here indicates that the 72 roots also consist of a set of 70 roots and two roots represented by the 8-tuples (½, ½, ½, ½, ½, ½, ½, ½) and (−½, −½, −½, −½, −½, −½, −½, −½). So the group-theoretical composition of the 72 roots is paralleled by the yod composition of the trunk and the root of the 1-tree.
The 240 yods needed to construct the 1-tree from Type A triangles divide into ten sets of 24 yods, which divide further into three sets of 24 and seven sets of 24. This 3:7 division is the Tree of Life counterpart of the three major whorls and seven minor whorls of the UPA/subquark state of the E8×E8 heterotic superstring (see here). The three major whorls, which carry the 72 gauge charges of E6, are the manifestation of the roots & trunk of the 1-tree, which contain 72 yods, whilst the seven minor whorls, which carry the 168 gauge charge of E8, are the manifestation of its branches, which contain 168 yods. The factorization: 168 = 7×24 is made possible by the facts that: 1. the branches of the 1-tree contain 14 triangles, and 2. each side of the 1-tree is the mirror image of the other. Five triangles (coloured dark or light shades of red, orange, yellow, green & blue) are on each side of the central Pillar of Equilibrium, which is straddled by four triangles coloured light & dark shades of indigo and violet. Two of the latter colours can be associated with each side. The dark shades of these two colours can be associated with one side of the 1-tree and the light shades can be associated with the other side. There are two hexagonal yods on a side shared by two triangles. One hexagonal yod is associated with one triangle and the second one should be regarded as associated with the other triangle. This allows 12 yods to be associated with each triangle. The 168 yods comprise 12 corners and 154 hexagonal yods, so that these 12 yods consist of one corner and 11 hexagonal yods. Therefore, the crucial factor of seven in the factorization arises simply from the fact that seven light-coloured triangles can be associated with the left-hand side of the 1-tree and seven dark-coloured triangles can be associated with its right-hand side. Each set of 24 yods consists of 12 yods associated with each side, so that the 168 yods divide into two sets of 84 yods, each set being associated with a set of seven triangles.
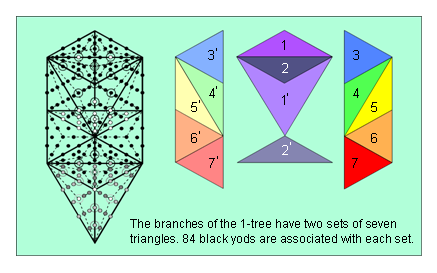 This 84:84 division was encountered in earlier analyses of sacred geometries and has been
discussed in many different contexts in previous articles. It manifests in the subquark as the outer and inner
halves of each helical whorl of the UPA, each having 840 circular turns that make 2½ revolutions around its
axis of spin, that is, 168 turns make a half-revolution and 84
turns make a quarter-revolution. Page 13 here displays the 240 roots of E8 as 8-tuples. Notice that the
168 roots of E8 that are not roots of E6 consist of three sets of 28
(i.e., 84 roots), a set of 56 & another set of 28 (i.e., 84 roots). So these 168 roots
divide naturally into two sets of 84 roots. Their counterparts in the branches of the 1-tree are the 84
yods that belong to the seven triangles associated with its left-hand or right-hand half.
This 84:84 division was encountered in earlier analyses of sacred geometries and has been
discussed in many different contexts in previous articles. It manifests in the subquark as the outer and inner
halves of each helical whorl of the UPA, each having 840 circular turns that make 2½ revolutions around its
axis of spin, that is, 168 turns make a half-revolution and 84
turns make a quarter-revolution. Page 13 here displays the 240 roots of E8 as 8-tuples. Notice that the
168 roots of E8 that are not roots of E6 consist of three sets of 28
(i.e., 84 roots), a set of 56 & another set of 28 (i.e., 84 roots). So these 168 roots
divide naturally into two sets of 84 roots. Their counterparts in the branches of the 1-tree are the 84
yods that belong to the seven triangles associated with its left-hand or right-hand half.
Four corners of tetractyses, four hexagonal yods at their centres & eight hexagonal yods on their sides (i.e., 16 yods) are aligned with the central Pillar of Equilibrium straddled by the four triangles. Hence, (168−16=152) yods belong to the branches in both halves of the 1-tree. 76 yods in the branches belong to each half, where 76 is the number value of YAHWEH ELOHIM, the Godname of Tiphareth. The eight hexagonal yods symbolizing the eight simple roots of E8 consist of four yods outside the 1-tree on either side of the Pillar of Equilibrium. Outside the trunk are (76+4=80) yods on either side, where 80 is the number value of Yesod. This is also the number of yods in the trunk when the (10+1) Sephirothic corners of the 19 triangles are included.
The 1-tree consists of 30 corners of 57 triangles with 82 sides, i.e., 112 corners & sides, where 112 is the number value of Beni Elohim, the Order of Angels assigned to Hod, and 87 corners & triangles, where 87 is the number value of Levanah, the Mundane Chakra of Yesod. The 1-tree consists of 169 points, lines & triangles. In other words, below its apex are 168 geometrical elements. The number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth, is the number of geometrical elements needed to construct the 1-tree, starting from the mathematical point represented by its apex. The lowest tree corresponds to Malkuth, the last Sephirah of Constriction. Here is yet more, truly amazing evidence that the gematria number values of the Kabbalistic names of the Sephiroth, their Godnames, etc have a geometrical basis.
| << Previous 1... 32 33 [34] 35 36 ...50 Next >> |