ARTICLE 54
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://smphillips.mysite.com
Abstract
The Tree of Life known to Kabbalah is but the outer form of the true cosmic blueprint. Its geometry generates an inner form that consists of two sets of seven enfolded, regular polygons, one set being the mirror image of the other. This article analyzes the properties of the combined outer and inner forms of the Tree of Life when the triangles in the former are either simple triangles, Type A or Type B and the polygons in the latter are either Type A or Type B. The geometrical and yod compositions of these combinations are numbers found to characterize other sacred geometries, confirming their equivalence to the Tree of Life demonstrated in previous articles. For example, 384 geometrical elements are outside the root edge when the outer Tree of Life has simple triangles and the inner Tree has Type A polygons. They consist of 192 corners & triangles and 192 sides. This pattern exists in other sacred geometries, e.g., each half of the 3-dimensional Sri Yantra with its 43 triangles turned into tetractyses has 192 yods. When triangles in the outer Tree are tetractyses, the combined Trees contain 496 hexagonal yods. This number is the dimension of the two Lie groups that define the unified superstring interaction. It demonstrates the Tree of Life basis of superstring theory. Furthermore, the 496 hexagonal yods consist of: 1. the 248 hexagonal yods either in the outer Tree, at the centres of the tetractyses in the first (6+6) enfolded polygons or in the two dodecagons, and 2. the 248 hexagonal yods surrounding the centres of tetractyses in the first (6+6) enfolded polygons. This corresponds to the 248:248 division of roots in E8×E8′, one of these superstring symmetry groups. 384 hexagonal yods line the sides of tetractyses as 192 pairs. This 192:192 division is characteristic of sacred geometries. With Type A triangles in the outer Tree and Type A polygons in the inner Tree, 480 geometrical elements are outside the root edge. They consist of 240 corners & triangles and 240 sides. This is analogous to the 480 non-zero roots of E8×E8' (one of the two Lie groups), which comprise 240 non-zero roots of E8 and 240 non-zero roots of E8'. The number of hexagonal yods in the combined Trees is that in the seven separate Type B polygons. The gematria number 620 of Kether is the number of yods outside the root edge that are hexagonal yods in both combined Trees. The tetractyses in the separate outer & inner Trees with Type B triangles and polygons have 248 corners, where 248 is the dimension of E8. There are 620 yods in the outer Tree other than corners and centres of its Type B triangles. 496 yods line its tetractyses that are not Sephiroth shared with its inner form. When their triangles and polygons are Type B, there are 240 corners outside the root edge in the combined outer & inner Trees of Life. ADONAI MELEKH, the Godname of Malkuth, prescribes the number of unshared yods outside the root edge that line tetractyses but are not located at the positions of the ten Sephiroth. With Type A triangles in the outer Tree and Type B polygons in the inner Tree, there are 192 corners outside the root edge. With Type B triangles in the outer Tree and Type A polygons in the inner Tree, there are 384 corners & triangles and 384 sides outside the root edge. Different combinations of these transformed Trees embody numbers characterising other sacred geometries. It is powerful evidence that the outer & inner Trees of Life constitute sacred geometry when combined as well as when separate.
1
Table 1. Gematria number values of the ten Sephiroth in the four Worlds.
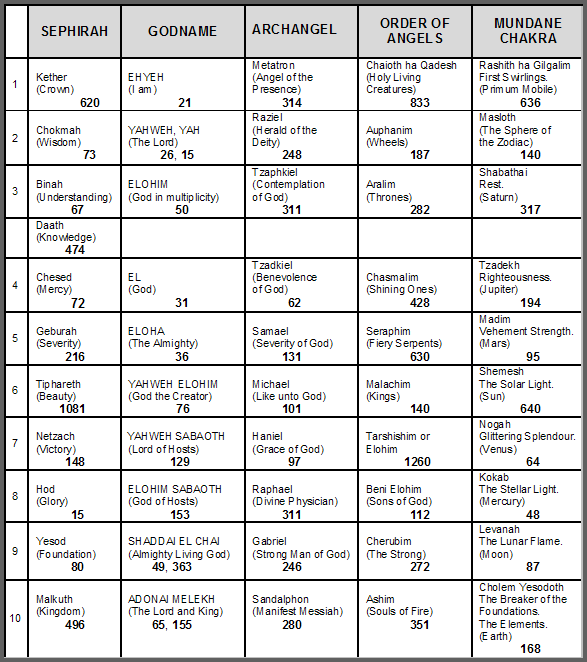
(Numbers in this table referred to in the article will be written in boldface).
2
1. Shared geometrical elements & yods
The outer Tree of Life consists of 16 triangles arranged in space in such a way that they have 10 corners and 22 sides. The inner Tree of Life comprises two sets of seven regular polygons: triangle, square, pentagon, hexagon, octagon, decagon & dodecagon. One set is the mirror image of the other, so that they lie in a single plane — that containing the Pillar of Mercy and the Pillar of Judgement. This means that the two vertical sides of sectors of the two hexagons coincide with the sides of triangles in the outer Tree that form the two outer pillars. It also means that the top and bottom corners of these two hexagons coincide with corners of triangles located at the positions of Chokmah, Netzach, Binah & Hod, whilst the outer corner of each triangle belonging to a set of polygons coincides with the corner of triangles that is located at Chesed and at Geburah, Hence, six green corners and four green sides, i.e., 10 corners & sides, of the outer Tree are shared with its inner form (Fig. 1). No triangles in the outer Tree are sectors of the 14 polygons, which number 94. This leaves it with 16 unshared triangles with four unshared corners and 18 unshared sides, i.e., 38 geometrical elements. The sectors have 80 corners (six shared, 74 unshared) and 175 sides (four shared, 171 unshared). Superposed, the outer & inner Trees of Life consist of 84 corners (six shared, 78 unshared), 193 sides (four shared, 189 unshared) & 110 unshared triangles. The 387 geometrical elements comprise 10 shared elements and 377 unshared ones.
Figure 1. The outer & inner Trees of Life have 10 shared geometrical elements and 16 shared yods.
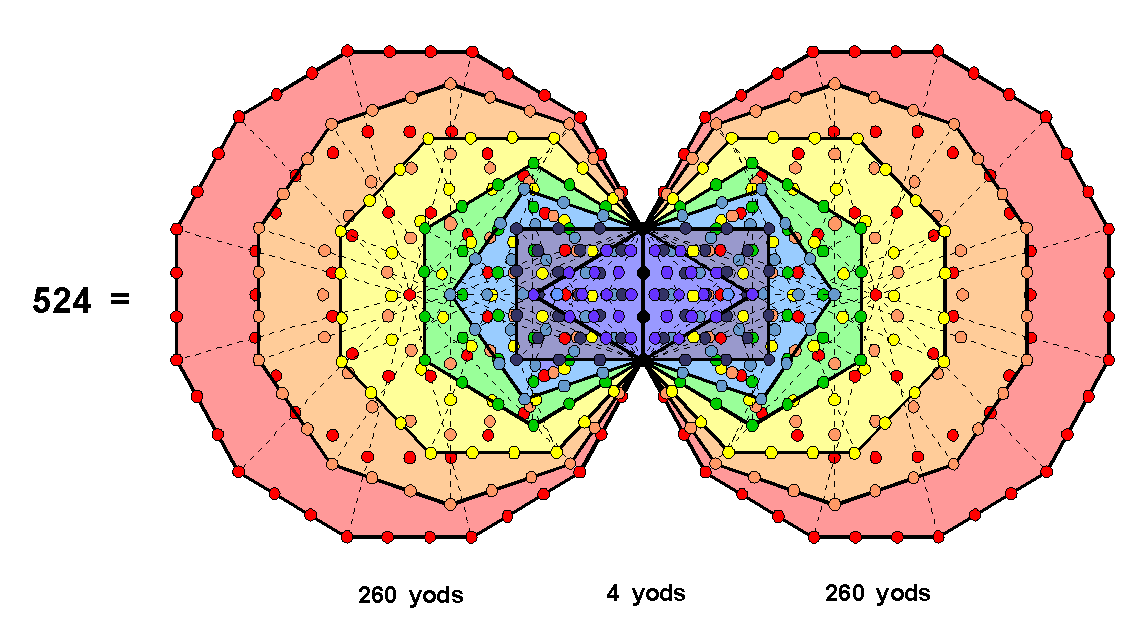
Transformed into tetractyses, the 16 triangles of the outer Tree contain 70 yods (10 corners, 60 hexagonal yods) and the 94 sectors of the 14 enfolded polygons contain 524 yods (80 corners, 444 hexagonal yods). There are eight hexagonal yods on the four vertical sides of the sectors of the two hexagons that are shared with the outer Tree of Life because they lie on its side pillars. Although the two hexagonal yods on the Chesed-Geburah Path are also the centres of the triangles belonging to the two sets of enfolded polygons, they still count as hexagonal yods in determining the hexagonal yod population of the combined Trees of Life. Although they are shared as yods along with eight hexagonal yods in the hexagons, these two yods are not shared as hexagonal yods. This is important to realize when we consider later the hexagonal yod population of the combined Trees. As well as these ten yods shared with polygons, three corners of tetractyses on each side pillar coincide with either the top and bottom of the hexagons or with the outer corner of the triangle belonging to each set of polygons. Hence, the outer & inner Trees share 16 yods. This leaves 54 green unshared yods in the former and 508 unshared yods in the latter (254 blue yods in the left-hand set of polygons in Figure 1 and 254 red yods in the right-hand set). Superposed, the outer & inner Trees have 578 yods (16 shared, 562 unshared).
We shall now analyze the properties of the combined Trees of Life when the outer one (henceforth to be called “OTL”) is composed of either simple triangles, Type A triangles or Type B triangles and when the
3
inner Tree of Life (to be called “ITL”) consists of either Type A polygons or Type B polygons.
2. Simple triangles in OTL & Type A polygons in ITL
Geometrical composition
As stated earlier, OTL has 16 triangles with 10 corners & 22 sides, i.e., 48 geometrical elements, where 48 is the number value of Kokab, the Mundane Chakra of Hod. ITL has 94 triangular sectors with 80 corners & 175 sides, i.e., it has 349 geometrical elements. Combined, they comprise 387 geometrical elements made up of 84 corners, where
84 = 12 + 32 + 52 + 72,
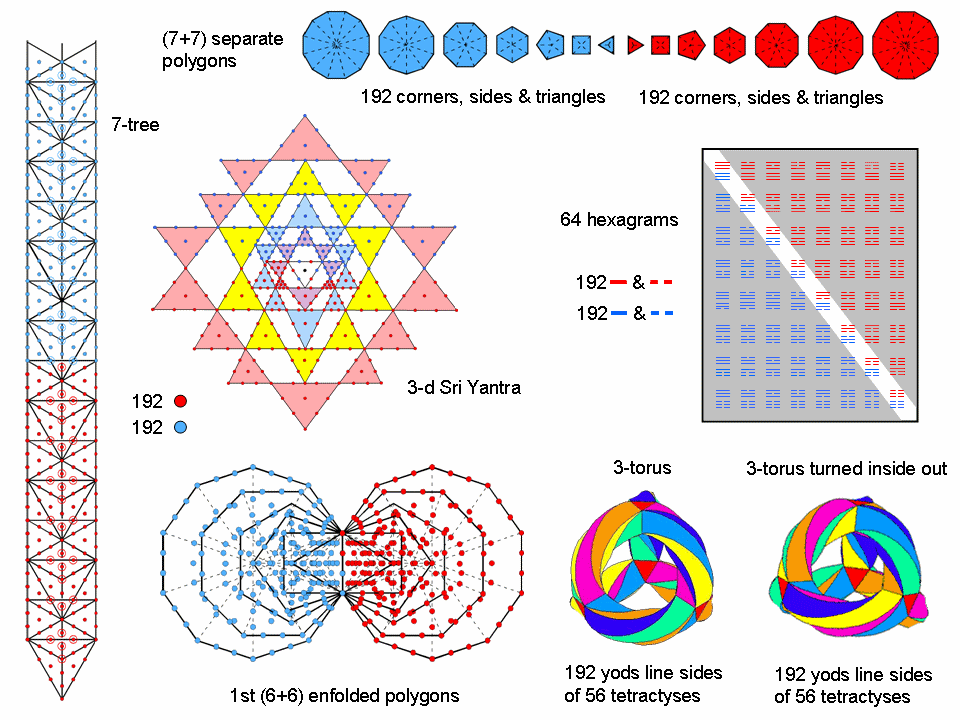
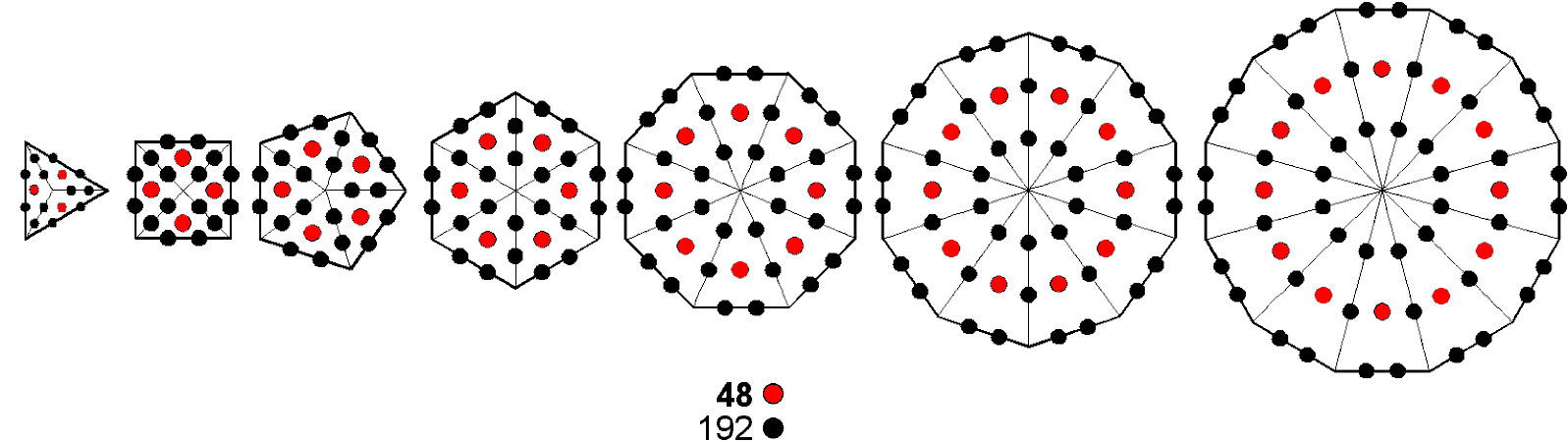
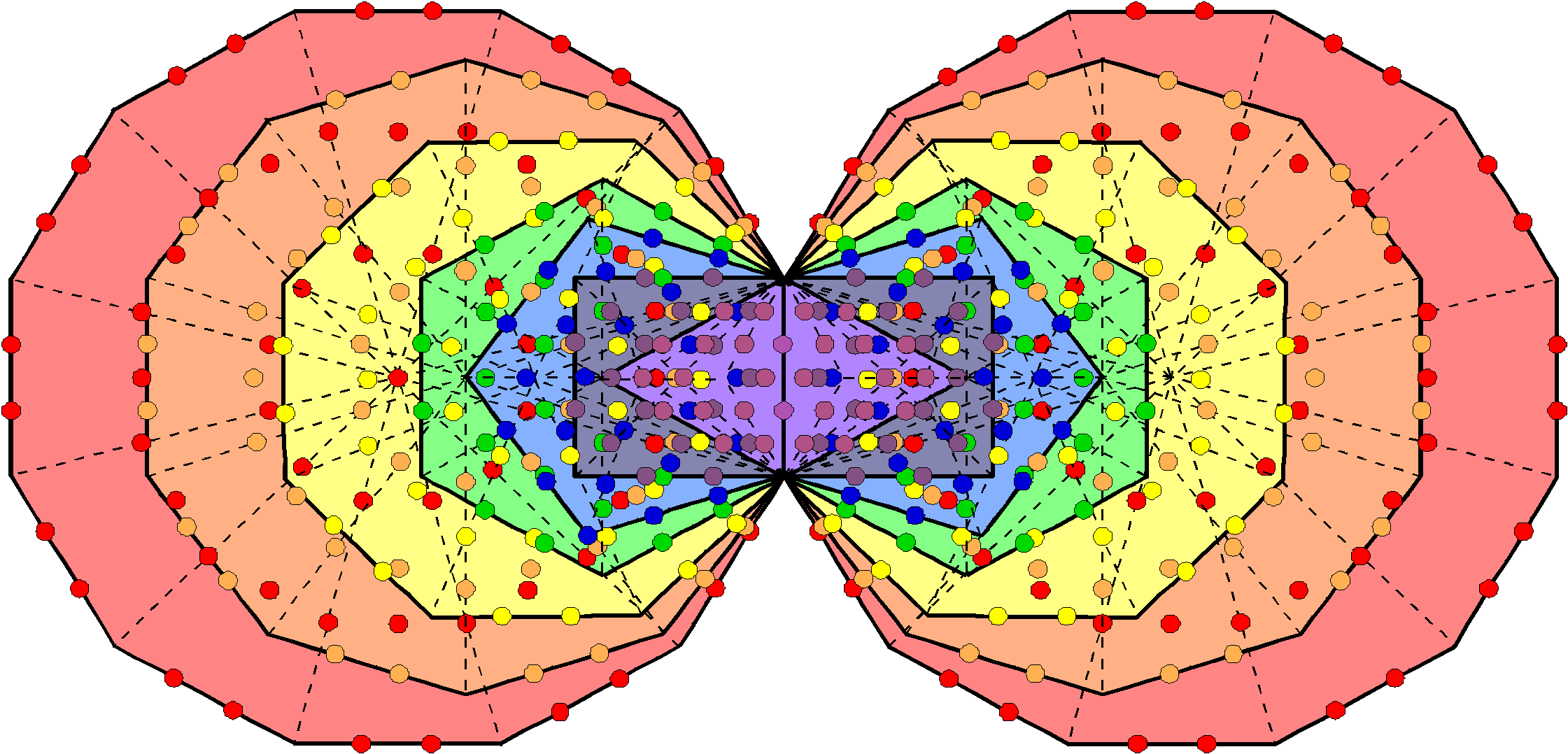
193 sides & 110 triangles. Outside the root edge are 384 geometrical elements: 192 corners & triangles and 192 sides. This 192:192 division manifests in ITL as the 192 corners & triangles in the 14 separate polygons and as their 192 sides (alternatively, as
Figure 2. The 192:192 pattern in various sacred geometries.
the 192 geometrical elements in each set of seven polygons). Figure 2 shows how this division appears in other sacred geometries.
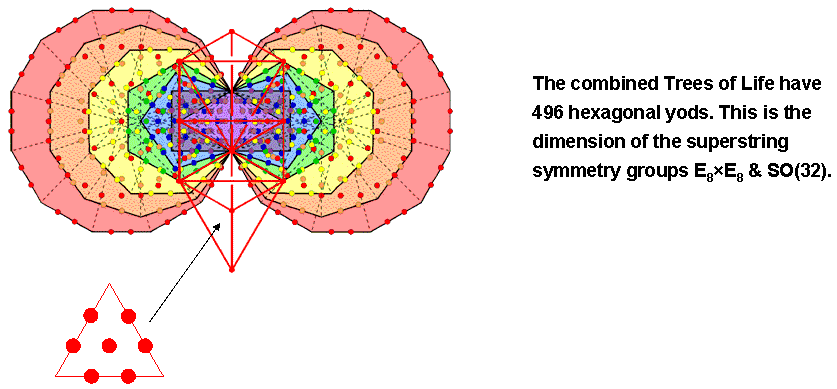
Figure 3. The combined outer & inner Trees of Life have 496 hexagonal yods. This is the dimension of the superstring symmetry groups E8×E8 and SO(32).
4
Yod composition
Combined, OTL & ITL contain 578 yods (see Fig. 1). Sixteen of them are shared and 562 are unshared. OTL has 60 hexagonal yods, eight of which are hexagonal yods in the pair of hexagons. ITL has 444 hexagonal yods. Remembering our earlier comment that the two hexagonal yods on the Chesed-Geburah Path still count as hexagonal yods even though they are corners of tetractyses in the two triangles belonging to ITL, the number of hexagonal yods in the combined OTL & ITL = 60 + 444 − 8 = 496 (Fig. 3). This is both the number value of Malkuth and the dimension of E8×E8 & SO(32) — the two symmetry groups with dimension 496 that allow interactions between superstrings that are free of quantum anomalies. What more explicit proof could there be that the Tree of Life encodes superstring theory — or, rather, M-theory, the so-called 'theory of everything' that contains the five versions of superstrings as approximations?
Figure 4.
Outer Tree of Life
Turned into tetractyses, the 16 triangles contain 60 hexagonal yods consisting of the 16 brown hexagonal yods at their centres and the 44 hexagonal yods on their 22 sides (Fig. 4). As four of these sides are sides of the sectors of the two hexagons belonging to the inner Tree of Life, its outer form has (22−4=18) sides with (18×2= 36) green hexagonal yods that are unshared with it as hexagonal yods and eight white hexagonal yods that are shared. Hence, the outer Tree has (16+36=52) unshared hexagonal yods. 52 is the 26 th even integer, showing how YAHWEH with number value 26 determines the population of intrinsic hexagonal yods in the outer Tree. The two hexagonal yods on the Chesed-Geburah Path are the centres of the two triangles belonging to the (7+7) enfolded polygons. This means that there are 50 hexagonal yods in the outer Tree that are hexagonal yods from the perspective of both Trees, showing how ELOHIM, the Godname of Binah with number value 50, prescribes this property.
Inner Tree of Life
Turned into tetractyses, the (47+47) sectors of the (7+7) enfolded polygons have 524 yods. They consist of 80 corners and 444 hexagonal yods, where 80 is the number of Yesod. The latter comprise (47+47=94) hexagonal yods at the centres of tetractyses and (444−94=350) hexagonal yods that line their sides. Each dodecagon has 48 hexagonal yods lining sides of tetractyses. The 46 yods outside the root edge consist of 22 pink hexagonal yods on its sides and 24 red hexagonal yods on internal sides of its 12 tetractyses. Hence, 46 = 22 + 24 and 350 = 46 + 2 + 46 + 256, where "2" denotes the two purple hexagonal yods on the root edge, there being 256 hexagonal yods outside it that line tetractyses in the first (6+6) enfolded polygons. Each set of the first six enfolded polygons has 35 sectors and the dodecagon has 12 sectors. Seventy of the 94 hexagonal yods at centres of tetractyses belong to the first (6+6) enfolded polygons; they are coloured purple. The 24 remaining hexagonal yods belong to the two dodecagons; they are coloured blue. Therefore,
444 = 350 + 94
= 46 + 2 + 46 + 256 + 70 + 24
= 22 + 24 + 2 + 22 + 24 + 256 + 70 + 24
= (70+2) + 24 + 22 + 24 + 22 + 24 + 256.
Combined outer & inner Trees of Life
When they are combined, the eight hexagonal yods on the side pillars of the outer Tree coincide with some of the hexagonal yods in the two hexagons. It was found above that there are 52 hexagonal yods in the outer Tree that are unshared as such with the inner Tree. The number of hexagonal yods in the combined Trees = 52 + 444 = 496. This is the dimension of both E8×E8 & SO(32), the two symmetry groups that govern the anomaly-free interactions between heterotic superstrings. This property constitutes amazing evidence for the Tree of Life basis of superstring theory because, although it might be coincidental, only the most extreme debunker would be willing to consider this a plausible possibility, especially given the additional properties of this number embodied by the combined Trees of Life to be discussed next.
Collecting together the various results discussed above:
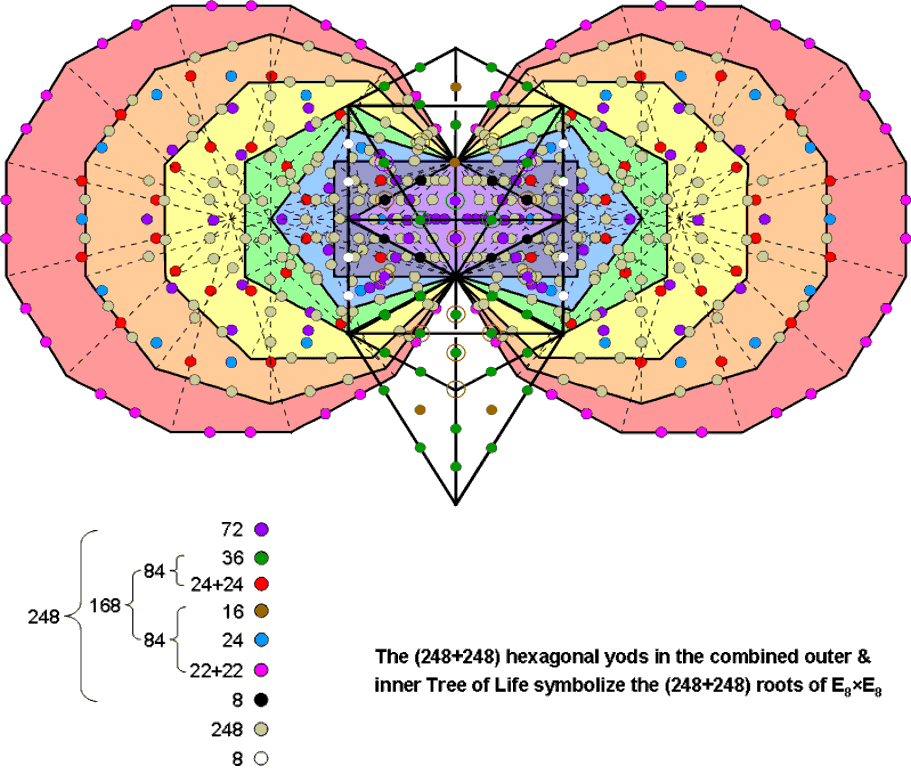
496 = 52 + 444 = (16+36) + (70+2) + 24 + 22 + 24 + 22 + 24 + 256.
The 256 hexagonal yods lining tetractyses in the first (6+6) enfolded polygons comprise eight black hexagonal yods on the four sides of the pair of triangles outside the root edge and 248 khaki hexagonal yods (let us write this set as 248′). Therefore,
496 = (16+36) + (70+2) + 24 + 22 + 24 + 22 + 24 + 8 + 248′ = 248 + 248′,
where
248 = (16+36) + (70+2) + 24 + 22 + 24 + 22 + 8 = 8 + (70+2) + (36+24+24) + (16+24+22+22)
= 8 + 72 + 84 + 84 = 8 + 72 + 168.
We find that the hexagonal yod population 496 naturally splits into 248 & 248′. This is analogous to how 496 is the sum of the dimension 248 of E8 and the dimension 248′ of E8′. That the geometry of the combined Trees allows such a natural splitting of this number into two equal numbers is evidence that it is not by chance that they have 496 hexagonal yods. This conclusion is confirmed by the fact that the number 248 further divides naturally into the number 8 denoting the eight simple roots of E8, the number 72 denoting the 72 roots of E6, an exceptional subgroup of E8, and the number 168 denoting the 168 remaining roots of E8. 168 further divides into two equal numbers 84 — a bifurcation that is displayed in all sacred geometries/holistic systems, as is the 72:168 division. What we are encountering here is not the highly improbable result of miraculous chance but the manifestation of the group mathematics of heterotic E8×E8′ superstring theory in the amazing sacred geometry of the outer & inner Trees of Life.
Let us next inspect whence the contributions to the 248 roots of E8 originate:
Notice that the 12 polygons embodying the number 72 constitute a holistic subset of the 14 polygons making up the inner Tree of Life, being characterized by the same parameters as those embodied in the complete set. Notice also that the hexagonal yods symbolizing the 168 roots come from the outer Tree (16+36) and from the dodecagon (24+22+24+22+24), which, too, is a holistic object. All the hexagonal yods symbolizing the second group E8′ come from the hexagonal yods in the first (6+6) enfolded polygons that surround the hexagonal yods at the centres of the 70 tetractys sectors of these polygons. In terms of the formal correspondence between yods and Sephiroth (see here), such yods correspond to the six Sephiroth of Construction above Malkuth in the outer Tree. Hence, the encoding of E8×E8′ in the combined Trees of Life suggests the following association:
E8 ↔ Malkuth;
E8 ′ ↔ 6 Sephiroth of Construction above Malkuth.
It would indicate that the symmetry group E8 applies to the forces operating in the familiar, physical universe of ordinary matter, namely, Malkuth, and that E8′ applies to forces operating in a more subtle (although still physical) universe. This is what superstring theorists have called the parallel universe of invisible "shadow matter" that is separated from the ordinary universe by a narrow gap extending along the seventh compactified dimension predicted by supergravity theories. This type of matter is sometimes confused by popular science writers with "mirror matter" — hypothetical particles that are the mirror images of the known subatomic particles. Although shadow matter is similar to this parity-reversed form of matter in not strongly interacting with ordinary matter, it is otherwise completely different, quite apart from being a rigorous, mathematical prediction of E8×E8′ heterotic superstring theory and not just a theoretical speculation.
OTL has 16 hexagonal yods at the centres of its 16 tetractyses and ITL has 94 hexagonal yods at the centres of its 94 tetractyses. The number of hexagonal yods lining the 193 sides of the (16+94=110) tetractyses in the combined Trees = 496 – 110 = 386. Outside the root edge of the (7+7) enfolded polygons are 384 hexagonal yods lining the 192 sides of the 110 tetractyses as 192 pairs. This number is a parameter of holistic systems, and its 192:192 division is characteristic of them, e.g.,
(See Fig. 2). As the combined Trees contain 578 yods, there are (578–386=192) corners of tetractyses and hexagonal yods at their centres.
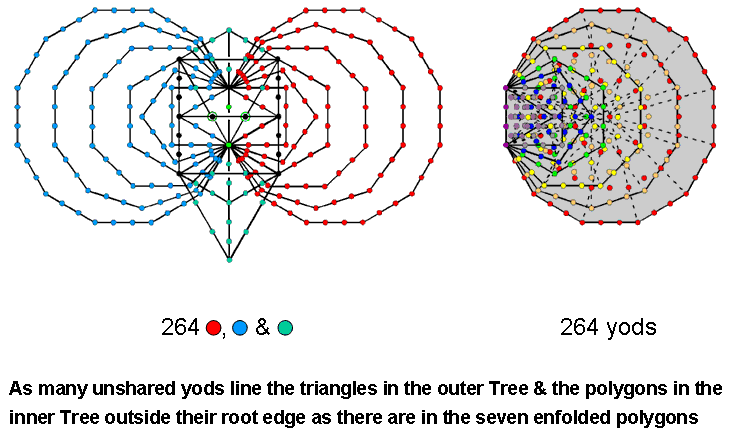
Figure 5. The combined outer & inner Trees of Life constitute a holistic system because the number of unshared yods lining their boundaries is the number of yods in the seven enfolded polygons.
Of the 578 yods in the combined OTL & ITL, 110 hexagonal yods are at centres of tetractyses, leaving 468 yods that line their 193 sides. They are made up of 54 yods in OTL ((54–16=38) unshared with ITL) and 414 yods in ITL. The counterpart in the latter of the 54 yods on the boundaries of the triangles is the set of 236 yods that line the sides of the 14 enfolded polygons. They include six yods at the positions of the Sephiroth on the two side pillars of OTL that also belong to the set of 54 yods. Therefore, the number of yods lining triangles in OTL and polygons in ITL = 54 – 6 + 236 = 284. The number of such boundary
5
yods outside the root edge = 284 – 4 = 280. This is the number value of Sandalphon, the Archangel of Malkuth. They include the 16 yods shared between OTL and ITL. There are (280–16=264) unshared, boundary yods outside the root edge. This is the number of yods in the seven enfolded polygons (Fig. 5). They include the four remaining Sephiroth on the central pillar: Kether, Tiphareth, Yesod & Malkuth. There are 260 (=26×10) unshared boundary yods other than Sephiroth in the combined OTL & ITL. This is the number of yods in the seven enfolded polygons outside their root edge. It demonstrates how YAHWEH, the Godname of Chokmah with number value 26, prescribes the combined Trees as well as ITL.
3. Type A triangles in OTL & Type A polygons in ITL
Let us, next, consider the case where both the triangles of OTL and the polygons of ITL are Type A.
Geometrical composition
Dividing each of the 16 triangles in OTL into their three sectors adds 16 corners and (3×16=48) sides, so that there are now 48 triangles with (10+16=26) corners (six shared, 20 unshared) and (22+48=70) sides (four shared, 66 unshared), i.e., 144 geometrical elements (10 shared, 134 unshared). The 94 sectors of the ITL have 80 corners (six shared, 74 unshared) and 175 sides (four shared, 171 unshared), i.e., 349 geometrical elements (10 shared, 339 unshared). The combined Trees of Life have 100 corners (six
Figure 6. The 7 separate polygons have 192 hexagonal yods on sides of 48 tetractyses and 48 hexagonal yods at their centres.
shared, 94 unshared), 241 sides (four shared, 237 unshared) and 142 triangles (all unshared), i.e., 483 geometrical elements (10 shared, 473 unshared).
Analogy with E8×E8
Outside the root edge in the combined OTL & ITL are 480 geometrical elements consisting of (98+142=240) corners & triangles and 240 sides. Compare this property with the fact that the 480 roots of the heterotic superstring symmetry group E8×E8 consist of 240 roots of the first group E8 and 240 roots of the second group E8. Replacing the 16 triangles in OTL by Type A triangles increases the 192 corners & triangles outside the root edge to 240 (16 extra corners & 32 extra triangles) and the 192 sides outside the root edge to 240 sides (48 extra sides). The counterpart of this 192→240 increase in the seven separate polygons is the fact that their 48 tetractys sectors have 192 hexagonal yods on their sides and 240 hexagonal yods in total (Fig. 6).
Figure 7. The 7 separate Type B polygons have 624 hexagonal yods.
6
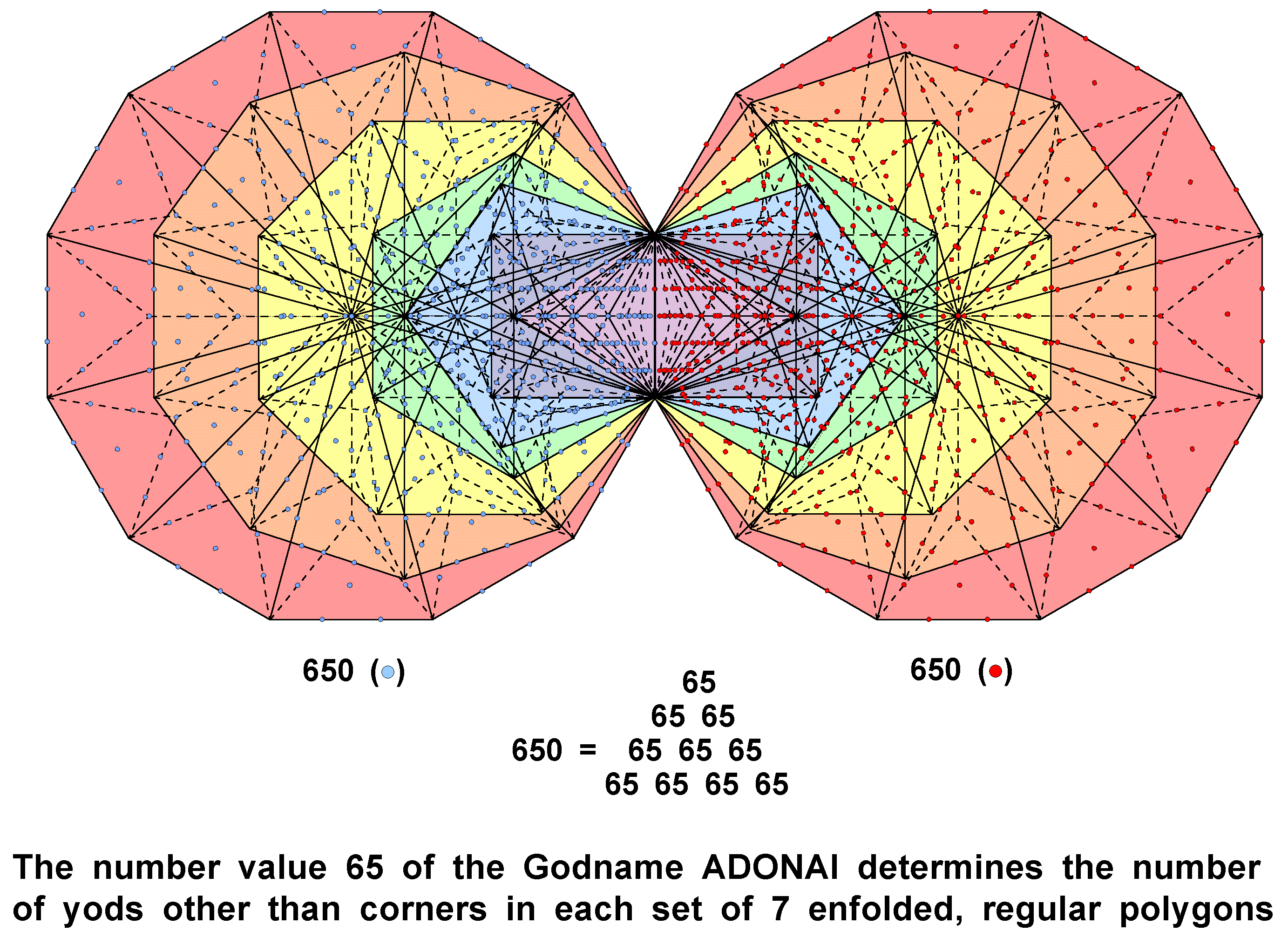
Figure 8. ADONAI prescribes the 7 enfolded Type B polygons.
7
Yod composition
Inside each of the 16 Type A triangles in OTL are one corner and nine hexagonal yods. We have seen that the combined Trees have 578 yods when the triangles in OTL are tetractyses. Now, nine yods are added per triangle, i.e., the yod population of the combined Trees = 578 + 16×9 = 722. The number of hexagonal yods in OTL = 22×2 + 16×9 = 188. ITL has 444 hexagonal yods, of which eight are shared with OTL. The number of hexagonal yods in the combined Trees of Life = 188 + 444 − 8 = 624. This is the number of hexagonal yods in the seven separate Type B polygons (Fig. 7).
The 16 triangles in OTL have (10+16=26) corners of 48 tetractyses; the 94 tetractyses in ITL have 80 corners, of which six corners are shared as such and two corners (centres of the two triangles) coincide with hexagonal yods on the Chesed-Geburah Path. Combined, OTL & ITL have (26+80−6−2=98) corners. Therefore, they have (624+98=722) yods, i.e., 718 yods other than the four yods in the root edge. Of these, 68 are corners of the (7+7) enfolded polygons. This leaves (718−68=650=65×10) yods outside the root edge that are not corners of polygons. Alternatively, the combined Trees have 650 yods other than corners of polygons and Sephiroth. This shows how ADONAI, the Godname of Malkuth with number value 65, prescribes the form of the combined Trees of Life.
Figure 9. The (7+7) enfolded polygons have 444 hexagonal yods.
ADONAI also prescribes the 650 yods associated with each set of seven enfolded Type B polygons that are not their corners, for both sets of enfolded polygons have 1370 yods, of which 70 are corners of polygons, leaving 1300 yods that are not corners, i.e., 650 yods associated with each set (Fig. 8). In each case, this number is the extra number of yods needed to construct the Trees, given their Sephirothic points and/or polygonal corners.
The 48 tetractyses in OTL with Type A triangles have 48 hexagonal yods at their centres. The 94 tetractyses in ITL with Type A polygons have 94 hexagonal yods at their centres. The number of hexagonal yods on the sides of the (48+94=142) tetractyses in the combined Trees of Life = 624 − 142 = 482. Just as there are 480 geometrical elements in them outside the root edge, so there are 480 hexagonal yods on the sides of the tetractyses outside their root edge. This is an amazing property. Eight of the 482 hexagonal yods are shared as such by both Trees, leaving (482−8=474) unshared hexagonal yods that line sides of tetractyses. 474 is the number value of Daath ("knowledge"), the non-Sephirah.
As calculated above, the combined Trees of Life have 722 yods. In the context of the two sets of the seven separate Type B polygons separated by the root edge, this is the sum of the two yods in the latter associated with each set and the 720 yods surrounding their seven centres.
The number value of Kether
The Type A triangle has 19 yods. Inside it are 10 yods. Inside the 16 Type A triangles of OTL are (16×10 = 160) yods that comprise 16 corners of tetractyses and (160−16=144) hexagonal yods. 44 hexagonal yods are on their 22 sides. The number of hexagonal yods in OTL = 144 + 44 = 188. They comprise 140 hexagonal yods on the 70 sides of the 48 tetractyses and 48 hexagonal yods at the centres of the latter. 140 is the number value of Masloth, the Mundane Chakra of Chokmah, and 48 is the number of Kokab, the Mundane Chakra of Hod.
ITL has 444 hexagonal yods when the 94 sectors of its (7+7) enfolded polygons are turned into tetractyses (Fig. 9). When OTL is superposed onto ITL, the centres of the two enfolded triangles, which
8
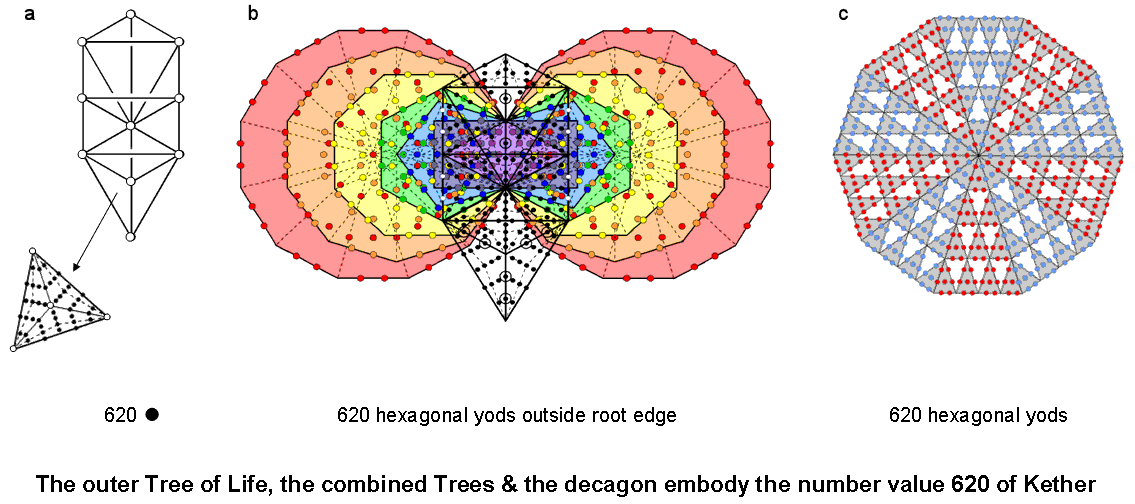
Figure 10. The outer Tree, the combined Trees & the decagon embody the gematria number 620 of Kether.
are corners of tetractyses, coincide with the two hexagonal yods on the Path connecting Chesed and Geburah, thereby removing them from the count of the number of hexagonal yods in the combined OTL & ITL, although they remain, of course, hexagonal yods as far as the former is concerned. Four white hexagonal yods on each side pillar coincide with hexagonal yods on the vertical, internal sides of the sectors of the two hexagons. The number of yods in the combined OTL & ITL that are hexagonal yods in both = 188 − 2 + 444 − 4 − 4 = 622. There are 620 such yods in the combined Trees outside the root edge of the (7+7) enfolded polygons (Fig. 10). This is the gematria number value of Kether, the first Sephirah of the Tree of Life.
4. Type B triangles in OTL & Type B polygons in ITLOuter Tree of Life
We found in Section 3 that the 16 Type A triangles in OTL consist of 26 corners and 70 sides of 48 triangles. Converting the Type A triangles into Type B triangles, i.e., dividing the 48 new triangles into their sectors, adds 48 corners and (3×48=144) sides, so that there are now (3×48=144) triangles with (26+48=74) corners and (70+144=214) sides, i.e., 432 geometrical elements. They include (74+214=288) corners & sides, where 288 = 11 + 22 + 33 + 44. Notice that the construction of the outer Tree of Life from Type B triangles generates (74−10=64=43) new corners and (214−22=192) new sides, i.e., (64+192=256=44) new corners & sides. Here we see how the Pythagorean Tetrad expresses the new properties of the sacred geometry of the Tree of Life when it undergoes higher-order transformations.
Inner Tree of Life
The geometrical composition of the (7+7) enfolded Type B polygons is tabulated below:
Corners Sides Triangles Total 7 enfolded polygons 88 229 141 458 (7+7) enfolded polygons 174 457 282 913
ELOHIM, the Godname of Binah with number value 50, prescribes the 229 sides of the 141 triangles in the seven enfolded Type B polygons because 229 is the 50th prime number. The (7+7) enfolded polygons have 910 (=91×10) geometrical elements outside their root edge, where
91 = 12 + 22 + 32 + 42 + 52 + 62
is one of the defining parameters of holistic systems, being, for example, the number of Trees of Life in the Cosmic Tree of Life. They include 282 triangles, where 282 is the number value of Aralim, the Order of Angels assigned to Binah.
Geometrical composition of the combined Trees
Separately, OTL & ITL have (74+174=248) corners, (214+457=671) sides & (144+282=426) triangles, where 248 is both the number value of Raziel, the Archangel of Binah, and the dimension of E8, the rank‑8, exceptional Lie group appearing in E8× E8 superstring theory. Amazingly, the separate outer and inner forms of the Tree of Life embody the dimension of the symmetry group generating the unified superstring force! When they are superimposed, the six Sephiroth on the two side pillars coincide with the
9
top and bottom corners of the two hexagons and their centres, whilst the two Paths on each side pillar coincide with internal sides of their sectors. To avoid double counting, these 10 geometrical elements must be subtracted. When combined, OTL & ITL, therefore, have 426 triangles with (248−6=242) corners and (671−2−2=667) sides, i.e., 1335 geometrical elements. There are 240 corners outside the root edge that consist of the (174−6–2=166) corners of the 282 triangles in ITL that are unshared with OTL and the 74 corners of the 144 triangles in the latter. The number 240 is a parameter of sacred geometries. The six corners on the side pillars of OTL that disappear when it is combined with ITL correspond to the six simple roots of E6 and the endpoints of the root edge correspond to the two remaining simple roots of E8.
The combined Trees of Life have (242+426=668) corners & triangles. There are (668−2–6=660) corners & triangles outside the root edge that are not shared between the two Trees. 660 = 66×10, where 66 is the 65th integer after 1. This shows how ADONAI, the Godname of Malkuth with number value 65, prescribes the form of the combined Trees.
The number of corners, sides & triangles in the combined Trees = 242 + 667 + 426 = 1335. The number of corners & sides = 242 + 667 = 909. The number of corners & sides outside the root edge that do not include shared, Sephirothic points = 909 − 3 − 6 = 900 = 90×10. The number 90 is a holistic parameter, being the sum of the 10 integers making up the Lambda Tetractys (1). As the table indicates that the (7+7) enfolded polygons have 913 corners, sides & triangles, of which two corners and one side make up the root edge and 10 corners & sides are shared with OTL, ITL has 900 intrinsic corners, sides & triangles outside the root edge. As there are 1332 geometrical elements outside the root edge, (1332–900=432) geometrical elements belong to OTL (422 unshared). It has (422+6=428) geometrical elements other than the four sides of triangles making up the two side pillars. 428 is the number value of Chasmalim, the Order of Angels assigned to Chesed.
The number of sides & triangles in the (7+7) enfolded polygons = 457 + 282 = 739. There are 369 sides & triangles on either side of the root edge. This is the sum of the number values of the Godnames of the first seven Sephiroth:
21 + 26 + 50 + 31 + 36 + 76 + 129 = 369.
Yod composition of the combined Trees
When the 282 triangles of ITL with Type B polygons are tetractyses, they contain 1370 yods. Inside each of the 16 primary triangles in OTL are 37 yods when it is a Type B triangle. Each of their 22 sides has two hexagonal yods. The number of yods in OTL when its 16 triangles are Type B = 10 + 22×2 + 16×37 = 646. Starting with the 10 corners of these triangles, its conversion into Type B triangles generates (646−10=636) yods, where 636 is the number value of Rashith ha Gilgalim, the Mundane Chakra of Kether. Separately, OTL & ITL have (646+1370=2016) yods. The seven yods on each side pillar are shared with ITL because they lie on sides of tetractyses in each hexagon. So are the two hexagonal yods on the Chesed-Geburah Path, because they are the centres of the two enfolded triangles. Hence, these have to be subtracted when the Trees are superposed in order to avoid double counting. The number of yods in the combined Trees = 2016 − 7 − 7 − 2 = 2000. 1370 yods belong to ITL and 630 yods belong to OTL, where 630 is the number value of Seraphim, the Order of Angels assigned to Geburah. The 14 polygons of ITL have 68 corners outside their shared root edge, six of which are shared with ITL. Hence, (68−6=62) polygonal corners outside the root edge are intrinsic to ITL (31 for each set of seven polygons), where 31 is the number value of EL, the Godname of Chesed and 62 is the number value of Tzadkiel, the Archangel of this Sephirah. The outermost corners of the two pentagons coincide with the centres of the decagons. Hence, 60 intrinsic corners outside the root edge are pure corners of polygons. The number of yods in the combined Trees of Life other than such corners = 2000 − 60 = 1940 = 194×10, where 194 is the number value of Tzadekh, the Mundane Chakra of Chesed. Here is a remarkable instance of three numbers appearing naturally in the same context that refer to the same Sephirah!
Of the 646 yods in OTL with 16 Type B triangles, 10 yods are at their Sephirothic corners and 16 yods are at their centres. There are (646−10−16=620) yods in OTL other than corners and centres of its triangles (Fig. 10). 620 is the number value of Kether, the first Sephirah of the Tree of Life. The polygonal counterpart of this property is the set of 620 hexagonal yods making up the decagon with 2nd-order tetractyses as its sectors.
The number of yods lining the 144 tetractyses in the 16 Type B triangles of OTL = 646 − 144 = 502. Six of these located at the positions of Sephiroth are shared with the (7+7) enfolded polygons. Hence, there are (502−6=496) yods on sides of tetractyses in OTL that are not Sephirothic points shared with ITL. This is how the outer Tree of Life embodies the number value 496 of Malkuth and the dimension of E8×E8 & SO(32), the two symmetry groups describing the forces between heterotic superstrings.
The number of yods lining the 282 tetractyses of ITL = 1370 − 282= 1088. There are (502+1088=1590) yods that line
10
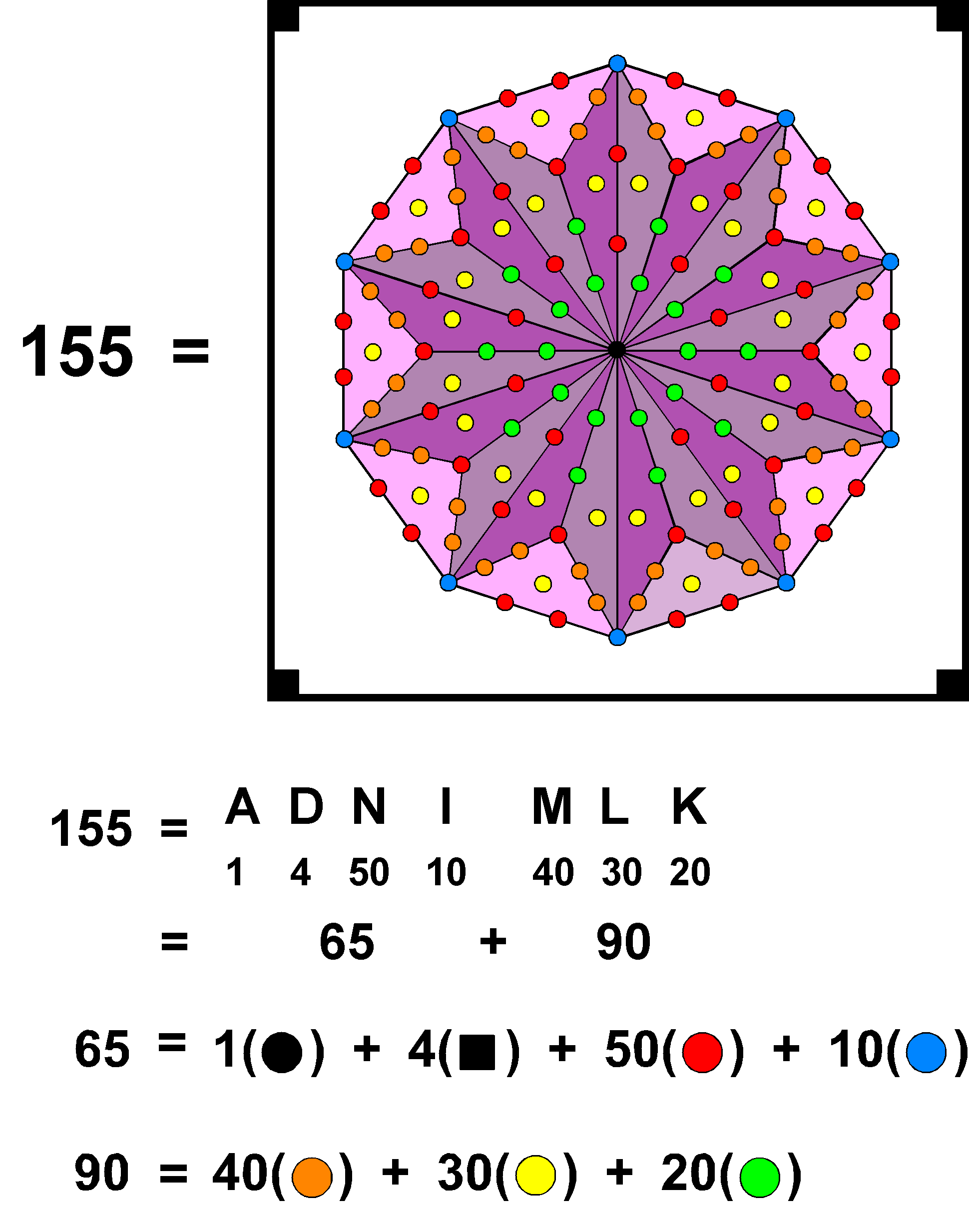
tetractyses in the separate Trees of Life. Remembering that the two hexagonal yods on the Chesed-Geburah Path become the centres of the two triangles belonging to the 14 enfolded polygons, the number of yods on sides of the (144+282=426) tetractyses in the combined Trees = 1590 − 7 − 7 − 2 = 1574. The number of such yods that are not shared = 1574 − 16 = 1558. They include the four yods of the root edge and the four Sephiroth on the central Pillar of Equilibrium. Hence, 1550 (=155×10) yods outside the root edge that line tetractyses are neither shared nor Sephiroth of OTL. This shows how ADONAI MELEKH, the Godname of Malkuth with number value 155, prescribes how many yods are needed to shape all the sectors of triangles making up the outer and inner forms of the Tree of Life.
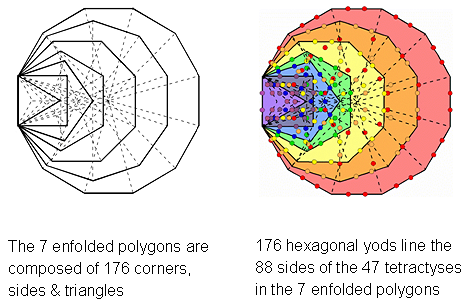
Inside each Type B triangle are 33 hexagonal yods. The number of hexagonal yods in OTL = 22×2 + 16×33 = 572. The 282 tetractyses in the (7+7) enfolded polygons have 174 corners and 1370 yods. Therefore, they have (1370−174=1196) hexagonal yods. Eight of these are shared with OTL as hexagonal yods. The number of hexagonal yods in the combined Trees of Life = 572 + 1196 − 8 = 1760. The seven enfolded Type A polygons have 176 hexagonal yods. This means that the 70 Type A polygons
Figure 11. The 7 enfolded polygons have 176 geometrical elements and 176 hexagonal yods on the sides of their tetractys sectors.
enfolded in 10 overlapping Trees of Life on each side of the central Pillar of Equilibrium have 1760 hexagonal yods. The combined Trees of Life with Type B triangles have as many hexagonal yods as are in the inner form of 10 Trees of Life with Type A polygons! This is remarkable, for it demonstrates how a single Tree of Life encodes its potential 10-fold development through a different order of transformation of its geometry. There are eight hexagonal yods shared by OTL & ITL and two hexagonal yods in the root edge.
Figure 12. Decagonal representation of the gematria number value of ADONAI MELEKH.
Hence, (1760−8−2=1750=175×10) hexagonal yods outside the root edge in the combined Trees are unshared. What emerges here is a differentiation that is analogous to the 175/176 distinction, reported by C.W. Leadbeater in his book Occult Chemistry (2), in the augmentation of major and minor whorls of the UPA, now identified by the author as the subquark state of the E8×E8 heterotic superstring. The number 175 determines the number of yods unshared by the inner and outer forms of 10 Trees and the difference 1 between 175 and 176 determines both shared hexagonal yods and hexagonal yods in the root edge. This quality of being shared by both the outer & inner forms of the Tree of Life is characteristic of this difference when it manifests in other sacred geometrical contexts. For example:
11
5. ADONAI MELEKH prescribes the combined Trees of Life
We found in Section 3 that the combined Trees of Life with Type A triangles & polygons have 650 yods other than Sephiroth and corners outside the root edge. As this is the number of yods in 65 tetractyses, ADONAI with number value 65 prescribes the combined Trees. We saw that it also prescribes ITL with Type B polygons because 650 yods other than polygonal corners are associated with each set of seven enfolded polygons. We found in Section 4 that ADONAI prescribes the combined Trees with Type B triangles & polygons because they have 660 (=66×10) corners & triangles outside the root edge that are unshared between them, where 66 is the 65th integer after 1. We also found that ADONAI MELEKH prescribes the combined Trees with Type B triangles & polygons because 155×10 yods outside the root edge that line their 426 tetractyses are neither Sephiroth nor shared. As 155 is the sum of the first 10 integers after 10:
11
12 13
155 = 14 15 16
17 18 19 20 .1550 is 10 times the sum of the first 10 integers after 10. It demonstrates how the Decad arithmetically determines this yod population of the combined Trees of Life. Figure 11 shows how the 10-sided, Type B decagon represents the number 155 as the gematria number value of ADONAI MELEKH. The letter values of the Godname denote the numbers of different types of yods.
ADONAI MELEKH prescribes OTL with Type A triangles
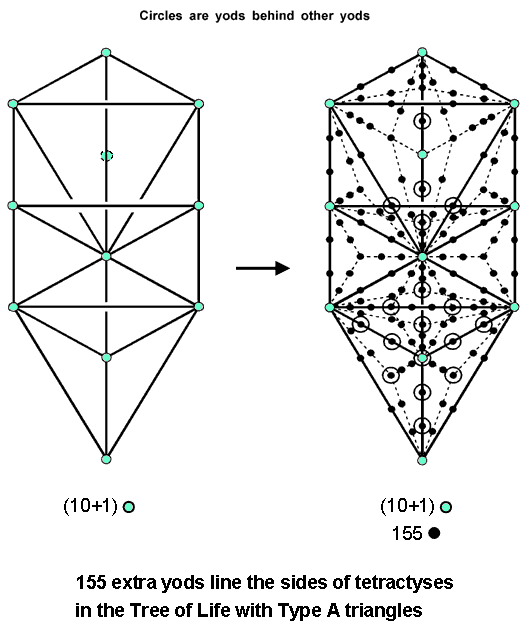
48 of the 214 yods in OTL are hexagonal yods at the centres of the 48 tetractyses making up the 16 Type A triangles with 10 corners and 22 sides. Therefore, (214−48=166) yods line the (22+48=70) sides of its 48 tetractyses. (10+16=26) of these are corners, leaving 140 hexagonal yods, where 26 is the number value of YAHWEH, the Godname of Chokmah, and 140 is the number value of Masloth, the Mundane Chakra of this Sephirah. The seven yods lining each side pillar of OTL and the two hexagonal yods on the Path connecting Chesed and Geburah are shared with the polygons of ITL, so that (166−16=150=15×10) yods lining the 70 sides of the 48 tetractyses in OTL are intrinsic to it. 15 is the number value of YAH, the older version of the Godname assigned to Chokmah.
12
Ten of the 166 yods lining the 70 sides of the 48 tetractyses are Sephiroth, leaving 156 yods, where 156 is the 155th integer after 1. This shows how ADONAI MELEKH prescribes the shape of OTL with Type A triangles. Starting with the 10 Sephiroth at the corners of these 16 triangles and with Daath at the centre of the triangle with Chokmah, Binah & Tiphareth located at its corners, (166−10−1=155) yods are needed to line the 70 sides of the 48 tetractyses in OTL (Fig. 13). Starting with a single, mathematical
Figure 13. 155 extra yods line the sides of tetractyses in OTL with Type A triangles.
point (Kether), 165 yods are needed to delineate these tetractyses, where
165 = 12 + 32 + 52 + 72 + 92.
The 16 Type A triangles in OTL have 48 sectors and the (7+7) Type B enfolded polygons consist of 282 triangles. Combined, they comprise 330 triangles, where
33
33 33
330 = 33 33 33
33 33 33 33and 33 = 1! + 2! + 3! + 4!. This number with well-known, Masonic significance is, therefore, a measure of the geometry of the combined OTL & ITL. Amazingly, the number 33 also determines the yod population of ITL, for this is 1370, which is the number of yods in 137 tetractyses, where 137 (the mysterious number in atomic physics whose reciprocal is the approximate value of the fine-structure constant) is the 33rd prime number!
As
55 = 12 + 22 + 32 + 42 + 52
and
385 = 7×55 = 12 + 22 + 32 + 42 + 52 + 62 + 72 + 82 + 92 + 102,
330 = 385 − 55 = 62 + 72 + 82 + 92 + 102.
The number of yods in n overlapping Trees of Life is given by
Y(n) = 50n + 20
(3). Therefore, the number of yods in every 31 Trees = Y(n+31) − Y(n) = 31×50 = 1550. As we found earlier, this is the number of unshared yods other than Sephiroth in the combined OTL & ITL that are outside the root edge and line tetractyses. We conclude that EL, the Godname of Chesed with number value 31, prescribes the yod population of the combined Trees.
6. Type A triangles in OTL & Type B polygons in ITL
When separate, OTL with Type A triangles has 26 corners, 70 sides & 48 triangles and ITL with Type B polygons has 174 corners, 457 sides & 282 triangles. Six corners and four sides become shared when they combine, so that they then have (26+174–6=194) corners, (70+457–4=523) sides & (48+282=330) triangles. 194 is the number value of Tzadekh, the Mundane Chakra of Chesed. Ten of the 104713
geometrical elements are shared, leaving 1037 unshared elements that consist of (194–6=188) corners, (523–4=519) sides & 330 triangles. The combined Trees have 192 corners outside the root edge. This is a parameter of ITL because 192 geometrical elements surround the centres of the seven separate polygons. Indeed, it is a defining parameter of all sacred geometries/holistic systems. For example, the 64 hexagrams in the I Ching system of divination have 192 lines and 192 broken lines, whilst each half of the 3-dimensional Sri Yantra constructed from tetractyses contains 192 yods (4).
Figure 14. The (7+7) enfolded polygons have 524 yods.
There are (194+330=524) corners & triangles. This number is par excellence a defining parameter of ITL because it is the number of yods in the (7+7) enfolded Type A polygons (Fig. 14). There are (194+523=717) corners & sides. Ten of them are shared between OTL and ITL, three of them make up the root edge and four are the corners located at the four Sephiroth on the central Pillar of Equilibrium. There are (717–10–3–4=700) corners & sides outside the root edge that are neither Sephiroth nor shared. This is the sum of the four separate tetractys arrays of integers making up the faces of the Tetrahedral Lambda (5), which is the arithmetic counterpart of sacred geometries.
OTL with Type A triangles has 214 yods (26 corners & 188 hexagonal yods). ITL with Type B polygons has 1370 yods (174 corners & 1196 hexagonal yods). Combined, they have (214+1370–16=1568) yods that comprise (26+174–6–2=192) corners and (188+1196–8=1376) hexagonal yods. They include six corners and eight hexagonal yods that are shared as, respectively, corners & hexagonal yods. Hence, they have (1568–6–8=1554) unshared yods that comprise (192–6=186) unshared corners and (1376–8=1368) unshared hexagonal yods. Outside the root edge with two endpoints and two hexagonal yods are 1550 (=155×10) unshared yods comprising 184 unshared corners and 1366 unshared hexagonal yods. Once again, the number value 155 of ADONAI MELEKH appears! The number 1366 is the number of yods outside the root edge in ITL with Type B polygons.
7. Type B triangles in OTL & Type A polygons in ITL
OTL with Type B triangles has 74 corners, 214 sides & 144 triangles. ITL with Type A polygons has 80 corners, 175 sides & 94 triangles. Combined, they have (74+80–6=148) corners, where 148 is the number value of Netzach, (214+175–4=385) sides, where
12
22 3 2
385 = 42 52 62
72 8 2 92 10 2 ,and (144+94=238) triangles. Their 771 geometrical elements comprise 10 shared elements and 761 unshared elements. Outside the root edge are (148+238–2=384) corners & triangles and (385–1=384) sides. This number is another parameter of holistic systems, being, for example, the number of lines & broken lines in the 64 hexagrams. There are (385+238=623) sides & triangles, i.e., 622 sides & triangles outside the root edge. We found in Section 3 that the combined OTL & ITL with Type A triangles & polygons have 622 hexagonal yods.
OTL with Type B triangles has 646 yods (74 corners & 572 hexagonal yods) and ITL with Type A polygons has 524 yods (80 corners & 444 hexagonal yods). Combined, they have (646+524–16=1154) yods that comprise (74+80–6–2=146) corners & (572+444–8=1008) hexagonal yods. They include six14
Figure 15. The number 138 as a holistic parameter.
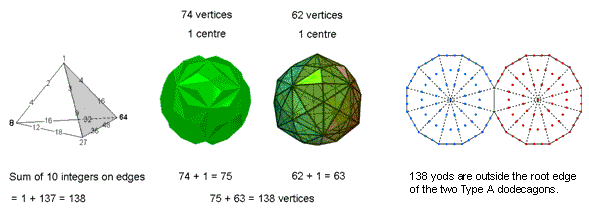
corners and eight hexagonal yods that are shared as such. Hence, they have (1154–6–8=1140) unshared yods that comprise (146–6=140) unshared corners and (1008–8=1000) unshared hexagonal yods, where 140 is the number value of Masloth, the Mundane Chakra of Chokmah. Outside the root edge are 1136 unshared yods that consist of 138 unshared corners and 998 unshared hexagonal yods. The number 138 is another parameter of holistic systems, being, for example:
Conclusion
Various transformations of the outer and inner forms of the Kabbalistic Tree of Life produce combinations that display geometrical and yod compositions characterized by the same numbers. These numbers have been shown in previous articles to be parameters of sacred geometries. This refutes the possibility that they arise merely by chance. Instead, it confirms that both these forms of the Tree of Life constitute sacred geometry. Two combinations are particularly interesting — Type A triangles/Type A polygons and Type B triangles/polygons. This is to be expected because only these combinations are consistent, mathematically speaking (clearly, it is inconsistent, from a strict mathematical point of view, for example, to treat the triangles in the outer Tree of Life as Type A but to regard the polygons — including the triangles — in the inner Tree as Type B). With Type A triangles & polygons, there are 240 corners & triangles and 240 sides outside the root edge. This 240:240 pattern manifests in the (7+7) separate Type A polygons as their (240+240) hexagonal yods. It appears in the first four Platonic solids as the 240 hexagonal yods in the faces of the tetrahedron, octahedron & cube and as the 240 hexagonal yods in the faces of the icosahedron. Their counterpart in superstring theory are the 240 roots of the two similar Lie groups E8 in E8×E8. The combined Trees of Life encode E8×E8 heterotic superstrings. That is the natural conclusion to be drawn for this version of the cosmic blueprint, for the only other explanation of the pattern is that it arises purely by coincidence and — given that it appears in these (and other) sacred geometries — this possibility has to be rejected as highly implausible. The hexagonal yod population of the combined Trees with Type B triangles & polygons embodies the same holistic parameter 176 as that determining the geometrical composition of the seven enfolded polygons. It manifests in the thickening, as reported by C.W. Leadbeater, of the major whorls of the UPA relative to its minor whorls, namely, every 25 spirillae of a given order are composed of 176 spirillae of the next higher order, not 175, as occurs in the minor whorls. ADONAI MELEKH, the Godname of Malkuth with number value 155, prescribes the shape of the combined Trees because their tetractyses have 1550 unshared yods that are not Sephiroth lining their sides outside the root edge.
References
1. Phillips, Stephen M. Article 11: “Plato’s Lambda — its meaning, generalisation and connection to the Tree of Life,” http://www.smphillips.mysite.com/pdfs/Article11.pdf.
2. Besant, Annie & Leadbeater, C.W. “Occult Chemistry,” 3rd ed., Theosophical Publishing House, Adyar, Chennai, India (1951), p. 23.
3. Proof: when they are turned into tetractyses, the (12n+4) triangles of n overlapping Trees of Life have (6n+4) corners and (16n+6) sides, two hexagonal yods lying on each side. The number of yods in n overlapping Trees = 6n + 4 + 2(16n+6) + 12n + 4 = 50n + 20.
4. Phillips, Stephen M. Article 35: “The Tree of Life nature of the Sri Yantra and some of its scientific meanings,” http://www.smphillips.mysite.com/pdfs/Article35.pdf.
5. Ref. 1, pp. 13, 14.
6. Phillips, Stephen M. Article 23: “The polyhedral Tree of Life,” http://www.smphillips.mysite.com/pdfs/Article23.pdf.
15