
The 8 Church Modes.
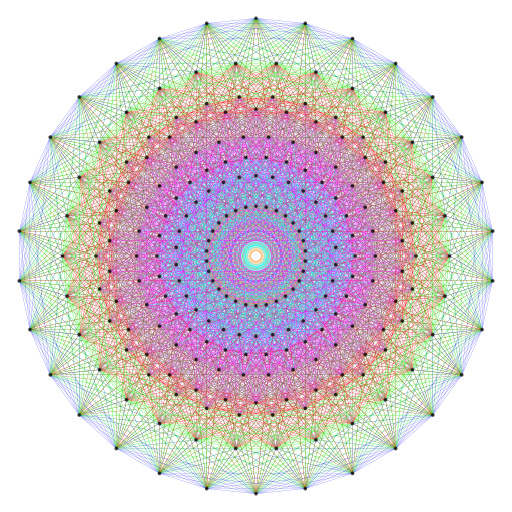
The 8 triacontagons in the E8 Coxeter plane projection of the 240 vertices of the
421 polytope.
| << Previous 1... 13 14 15 16 [17] Next >> |
17. The 8 Church modes as the musical counterpart of the pattern of 8 triacontagons in the E8 Coxeter plane projection of the 421 polytope
 |
 |
The 8 Church Modes. |
|
If the 421 polytope is truly an archetypal object whose E8 symmetry embodies the superstring physics of matter, one should expect to see correspondences in its geometry with not only sacred geometries but also the 7 types of diatonic scales or the 8 musical modes, which the author has shown in earlier articles correlate with the 64 hexagrams of the I Ching, the Sri Yantra, the inner form of the Tree of Life and other sacred geometries. And, indeed, one does see this! This page will reveal how the 8 Church modes manifest the 24:168 pattern that is characteristic of holistic systems and which appears in the triacontagon, the Petrie polygon of the 421 polytope, as previous pages in this section have shown. The musical analogy is too detailed to be due to chance (see below). Instead, it indicates that a fundamental pattern embodied in sacred geometries pervades different types of systems ranging from E8×E8 heterotic superstrings and DNA to the ancient Mesopotamian heptachords and the ancient Greek musical modes that were part of the historical origins of the 8 musical modes used in the plainsong of the Catholic Church (for background, see Article 14 and pp. 1-16 of Article 16). This holistic pattern is discussed in detail in The holistic pattern.
 |
|
|
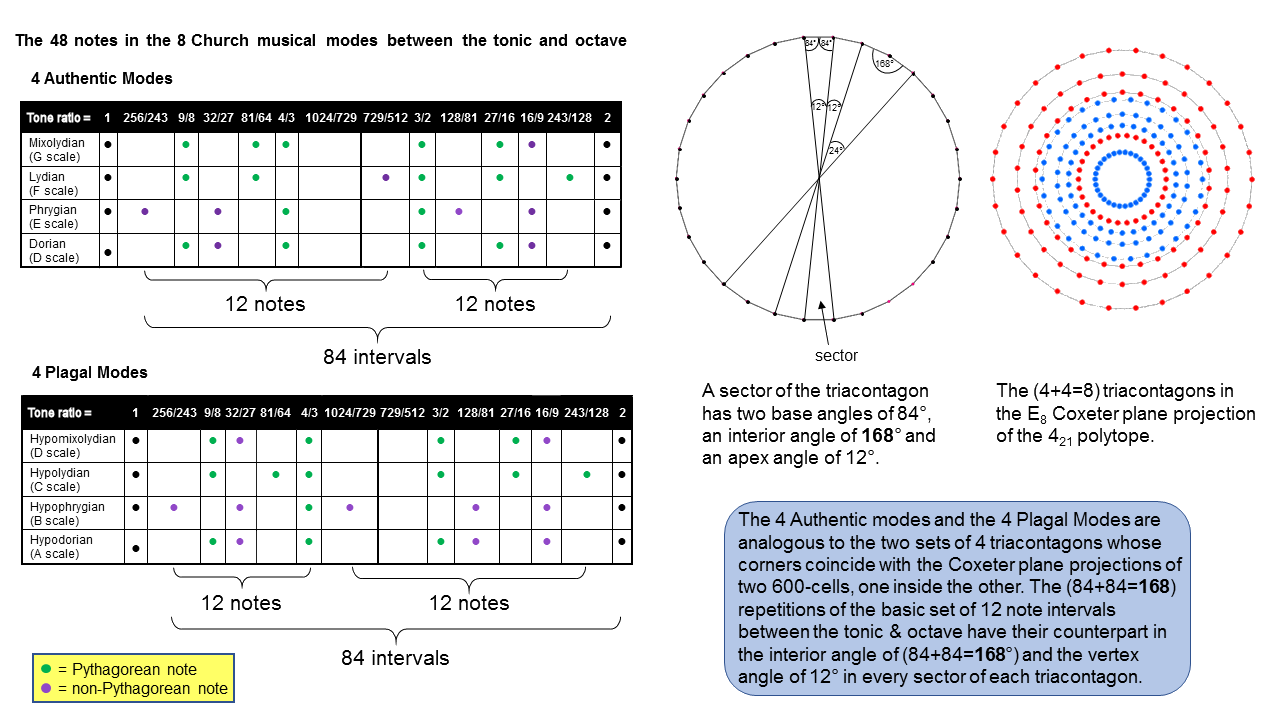
Earlier articles (e.g., Article 42) established that the 7 types of diatonic scales with Pythagorean tuning contain 12 types of notes between the tonic (1) and octave (2). In order of increasing tone ratios, they are:
| 1 | 256/243 | 9/8 | 32/27 | 81/64 | 4/3 | 1024/729 | 729/512 | 3/2 | 128/81 | 27/16 | 16/9 | 243/128 | 2 |
The 12 types of notes comprise the 6 notes between the tonic and octave of the Pythagorean musical scale and 6 notes that are non-Pythagorean (written above in red). Including the tonic and octave, there are 7 pairs of notes and their inversions (N.B. the inversion of a note N with tone ratio n is the note whose tone ratio is the interval 2/n between N and the octave):
|
The 14 types of notes in the 8 Church Modes |
The 12 different notes in the 7 diatonic scales between the tonic and octave consist of 6 pairs of notes up to that with tone ratio 1024/729 and their inversions. Notice that the perfect fourth and its inversion — the perfect fifth — are the only pair amongst the 7 pairs of notes and their inversions that are both Pythagorean notes.
The number of combinations of n objects taken r at a time is the binomial coefficient nCr = n!/r!(n−r)!. Given that the interval between a note with tone ratio n and a note with tone ratio m is m/n, the number of intervals between the 8 notes of a musical octave is the number of pairs of different notes that can be chosen from them. This is 8C2 = 28. Of these, 7 intervals are those between the tonic and the 7 higher notes, leaving 21 intervals between the latter. Hence, between the tonic and octave are 6 notes, with 21 intervals between the last 7 notes. The 8 Church musical modes comprise 4 so-called "Authentic Modes": Dorian (D scale), Phrygian (E scale), Lydian (F scale) & Mixolydian (G scale) and 4 so-called "Plagal Modes": Hypodorian (A scale), Hypophrygian (B scale), Hypolydian (C scale) & Hypomixolydian (D scale). Seven Modes are distinct octave species, the C scale (Hypolydian Mode) being the Pythagorean scale. The Dorian and Hypomixolydian Modes are essentially the same (D) scale in terms of their sequences of notes. The former starts the sequence of generation of Modes and the latter completes the cycle, so that it consists of the same sequence of notes. This means that each set of 4 Modes distinguishes one Mode, which either starts or finishes the eightfold cycle, from the 3 other Modes. The Dorian and Hypomixolydian Modes also differ from the 6 others in that their identical pattern of intervals between successive notes is the same as the pattern in reverse order; they are their own mirror image. Each set of 4 Modes comprises (4×6=24) notes between the tonic & octave. They are displayed in the picture above by green dots for Pythagorean notes and purple dots for non-Pythagorean notes. The 4 Authentic Modes have 16 Pythagorean notes and 8 non-Pythagorean notes; the 4 Plagal Modes have 14 Pythagorean notes and 10 non-Pythagorean notes. We see that the 8 Modes have 30 Pythagorean notes and 18 non-Pythagorean notes. Each set of 4 Modes have (4×6=24=4!) notes between the tonic & octave and (4×21=84) intervals between their last 7 notes, where
84 = 12 + 32 + 52 + 72 = 41 + 42 + 43 = 4 + 8 + 12 + 16 + 20 + 24,
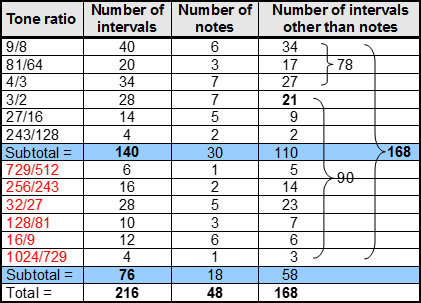
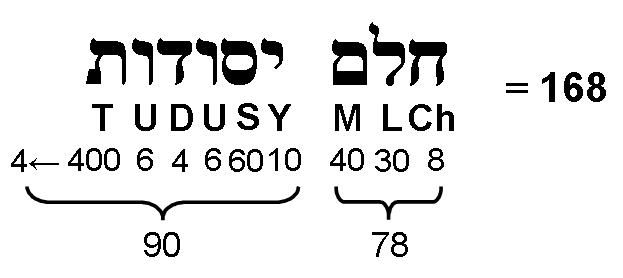
i.e., 84 is the sum of the 6 even integers from 4 to 4! that are 4 units apart. This illustrates how the Tetrad expresses two parameters of each set of 4 Modes. It means that between the tonic and octave of the complete set of 8 Modes are (24+24=48) notes with (84+84=168) intervals between the last 7 notes in each Mode. The number value 168 of Cholem Yesodoth, the Mundane Chakra of Malkuth, appears as the number of intervals between these last 7 notes; 168 = 8×7C2. Confirmation that this is not just an arithmetic coincidence is provided by the table below, which shows that the gematria number value 78 of Cholem is the number of intervals other than notes that are major seconds, major thirds or perfect fourths, whilst the number value 90 of Yesodoth is the number of the 9 remaining types of intervals that make up the 8 Modes:
 |
 |
|
|
|
If these two Kabbalistic numbers were the sums of numbers randomly taken from the list shown above, it could not be convincingly argued that this is evidence for the number values of both words being naturally generated. But what are the chances that the first 3 types of Pythagorean notes with tone ratios 9/8, 81/64 & 4/3 (i.e., a set of consecutive types of notes) would, by coincidence, generate the number value of one of these words? Obviously, they are small. This argues against the appearance of Kabbalistically significant numbers being due to chance because, if this were so, they would be the sum of numbers scattered randomly throughout the list. They would not be the sum of three consecutive numbers (all referring to Pythagorean notes) that start from the lowest one — hardly a random sequence!
For a musical scale with 8 notes, there are 8 unit intervals between each note and itself and 28 intervals between pairs of different notes. This makes a total of 36 intervals. They include the unit intervals between the 6 intermediate notes and themselves. There are (36−6=30) other intervals. They comprise the 21 intervals between the 7 notes above the tonic, all 8 note intervals and the unit interval (the tonic, of course, also has a tone ratio of 1, but this is conceptually different from the unit interval, which is not a note but the ratio of the tone ratios of a note and itself). A minimal set of 30 intervals (tonic+28 intervals+unit interval) define each Mode when we view it as a sequence of 8 notes that can start from a given note of any octave, i.e., the tonic need not be exactly the same note for each Mode (it could be a different octave), so that is why it must be counted for every Mode, despite its tone ratio having the same magnitude as the unit interval. The 8 Modes have (8×30=240) such intervals that exclude the redundant unit intervals between the 6 intermediate notes of each Mode and themselves They comprise the (8×21=168) intervals between their last 7 notes and the [8×(1+8)=72] intervals that are either notes or unit intervals. The 12 basic notes between the tonic and octave are repeated 36 times as notes, although, of course, not in equal numbers. As intervals that are not notes, they are repeated 168 times. According to the table above, the 168 intervals consist of 110 Pythagorean intervals and 58 non-Pythagorean ones. They comprise 118 intervals up to 1024/729 and 50 higher intervals (inversions of the former).
These results may be summarised in the following equations:
240 = 24 + 12 + 36 + 168,
= 8×(3 + 6 + 21),
= 8×30,
where "24" = 8 tonics + 8 octaves + 8 unit intervals, "12" = 12 basic notes, "36" = 36 repetitions of the basic notes, "168" = 168 intervals that are not notes, "3" = tonic + octave + unit interval, "6" = 6 notes between tonic & octave in a Mode and "21" = 21 intervals between the last 7 notes in a Mode.
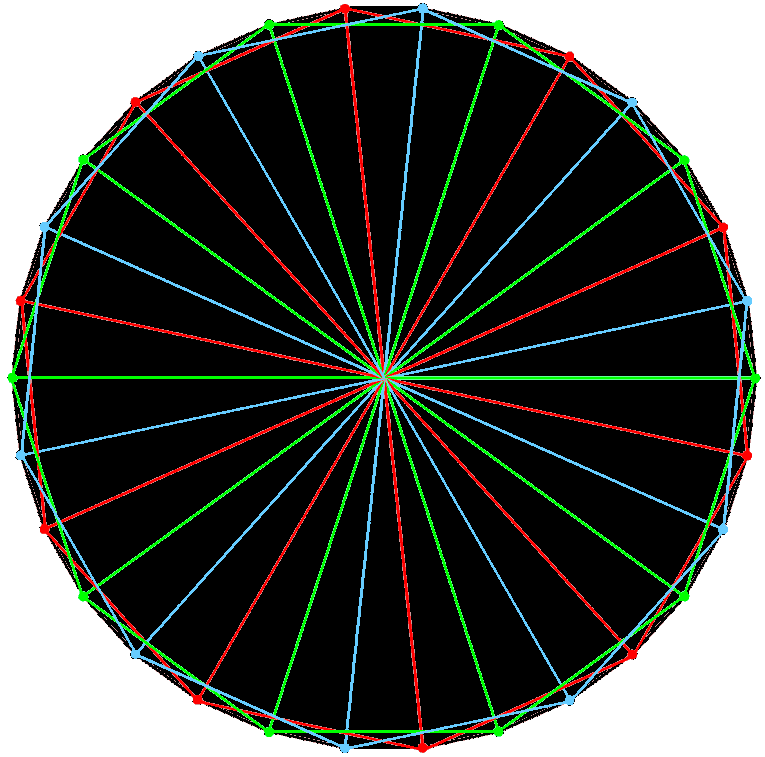
The following correspondences emerge between the 8 Church Modes and the 8 triacontagons formed by the E8 Coxeter plane projection of the 240 vertices of the 421 polytope:
|
1. |
8 Church Modes | ↔ | 8 triacontagons. |
| 2. | 4 Authentic Modes + 4 Plagal Modes | ↔ | 4 triacontagons associated with a 600-cell and 4 triacontagons associated with a smaller 600-cell inside it. |
| 3. | Each set of 4 Modes = (1+3) Modes | ↔ | Each set of 4 triacontagons has 3 triacontagons surrounding the smallest one. |
| 4. | 24 notes between tonic & octave in each set of 4 Modes | ↔ | 2 adjacent sectors enclose vertex angles of (12+12=24°). |
| 5. | 24 notes comprise 4 sets of 6 notes between tonic & octave | ↔ | Each pair of adjacent sectors is 4 right angled-triangles with vertex angles of 6°. |
| 6. | (4×21=84) intervals between last 7 notes in each set of 4 Modes | ↔ | Base angle of sector of triacontagon = 84°. |
| 7. | (84+84=168) intervals between last 7 notes in (4+4) Modes | ↔ | Interior angle enclosed by sides of adjacent sectors =168°. |
| 8. | 30 Pythagorean notes in (4+4) Modes | ↔ | The (4+4) triacontagons are 30-gons. |
| 9. | 30 intervals in a Mode, excluding unit intervals between 6 notes and themselves | ↔ | Triacontagons are 30-gons. |
| 10. | (8×30=240) intervals in 8 Modes excluding unit intervals between (8×6=48) notes and themselves | ↔ | 8 triacontagons have 240 corners. |
|
11. |
8 notes make up an octave of a Mode. |
↔ |
The 8-dimensional roots of E8 have 8 coordinates. |
It cannot, reasonably, be denied that there are too many analogous features to be dismissed as coincidental. Why, therefore, do they exist? It can be only because a universal design exists that generates analogous features in systems that might otherwise not be thought to be conceptually related in any way — such as the 8 musical Modes and the physics of vibrating superstrings. The truth may be that all systems will be found to be analogous provided that they are, truly, holistic, thereby embodying in their own way this archetypal pattern. The problems are how to recognise such systems for what they are and how to exploit their analogous features in order to learn more about the little-understood ones. The author's website provides the criteria and information that make this task possible.
The 240 corners of the 8 triacontagons are the projections in the E8 Coxeter plane of the 240 vertices of the 421 polytope, which coincide with the 240 root vectors in the 8-dimensional lattice space of E8. What has been shown here is that every root of E8 defining a gauge charge carried by E8×E8′ heterotic superstrings corresponds to an interval between the notes in the 8 musical Modes. The correspondence is completed by realising that every musical interval can be either rising with an interval of n or falling with an interval of 1/n, so that there 240 gauge charges of a second E8 group that correspond to the falling intervals between the notes in the 8 Modes. The musical analogy with superstrings requires the existence of an identical second Lie group E8′ to accompany E8. There are 168 roots of E8 that are not also roots of its exceptional subgroup E6; they correspond to the 168 intervals between the last 7 notes in the 8 Modes. The remaining 72 roots are those of E6 and correspond to the 72 intervals that are either notes of each Mode or the unit interval repeated 8 times for the 8 Modes: 72 = 8×8 + 8×1.
As
240 = 8×30 = 8×3×10,
where 10 = 3 + 7,
240 = 8×3×(3+7) = 8×(9+21) = 72 + 168.
The division of the number 10 (Decad) into 3 and 7 expresses the separation of the 10 Sephiroth into the 3 members of the Supernal Triad and the 7 Sephiroth of Construction. Its arithmetic consequence is the dividing of the number 240 into the numbers 72 and 168. It appears in the 8 triacontagons as the division of the 30 corners of each triacontagon into 3 decagons (coloured red, green & blue in the picture shown below):
 |
 |
 |
72:168 division of the 240 roots of E8. |
The 3 decagons (red, green & blue) in the triacontagon. |
72:168 division in the (120+120=240) yods that line the sides of the two separate sets of the 7 enfolded polygons of the inner Tree of Life. |
Each decagon comprises a set of 3 consecutive corners and a set of 7 consecutive corners, so that all 3 decagons generate a set of 9 corners and a set of 21 corners. Each set of 4 triacontagons has a set of (4×9=36) corners and a set of (4×21=84) corners. The counterpart in the inner form of the Tree of Life of this 72:168 division for all 8 triacontagons is displayed by the 240 yods that line the boundaries of the two separate sets of 7 enfolded polygons constructed from 1st-order tetractyses. Each set has 36 black corners of polygons and 84 red hexagonal yods lining their sides, so that both sets have 72 black corners and 168 red hexagonal yods. The 120 intervals making up the 4 sets of 30 intervals between notes in the 4 Authentic Modes are symbolised by the 120 boundary yods in one set of enfolded polygons; the 120 intervals between notes in the 4 Plagal Modes are symbolised by the 120 yods lining the 42 sides of the mirror-image set of 7 polygons. The 36 corners in each set correspond to the 4 sets of nine intervals (8 notes+unit interval) and the (2×42=84) hexagonal yods in each set correspond to the 84 intervals between the last 7 notes in either the 4 Authentic Modes or the 4 Plagal Modes. The factorisation: 84 = 4×21 of the intervals between the last 7 notes in each set of 4 Modes manifests in each set of 7 enfolded polygons as the 21 pairs of hexagonal yods in the triangle, square, pentagon & dodecagon and as the 21 pairs of hexagonal yods in the hexagon, octagon & decagon. i.e., as 4 sets of 21 hexagonal yods.* The same 72:168 division manifests in other sacred geometries (see here & here). It manifests in the UPA as its 3 major whorls, which carry 72 gauge charges of E8 and correspond to the Supernal Triad, and as its 7 minor whorls, which carry 168 E8 gauge charges and correspond to the 7 Sephiroth of Construction. The natural existence of this division in the Modes is evidence for the holistic nature of both the 8 Modes and the 8 triacontagons in the E8 Coxeter plane projection of the 421 polytope. One of the most famous objects in mathematics, the 421 polytope is the geometrised expression of the 8 Church Modes.
The 72 intervals that are either notes or unit intervals comprise the 48 notes between the tonic and octave and 24 intervals that are either the tonic, octave or unit intervals. This 24:48 division of the number 72 corresponds in the root composition of E8 to the 72 roots of E6 and the 48 roots of its rank-4 exceptional subgroup F4. In other words, these roots correspond to the 48 notes between the tonic and octave, the remaining 24 roots in E6 corresponding to the 8 tonics, the 8 octaves & the 8 unit intervals. The 48 root vectors of F4 are the vertices of the 24-cell in two dual configurations:
24-cell vertices:
24 roots ((±1, ±1, 0, 0) and all permutations of coordinates);
Dual 24-cell vertices:
8 roots ((±1, 0, 0, 0) and all permutations of
coordinates);
16 roots (±½, ±½, ±½, ±½).
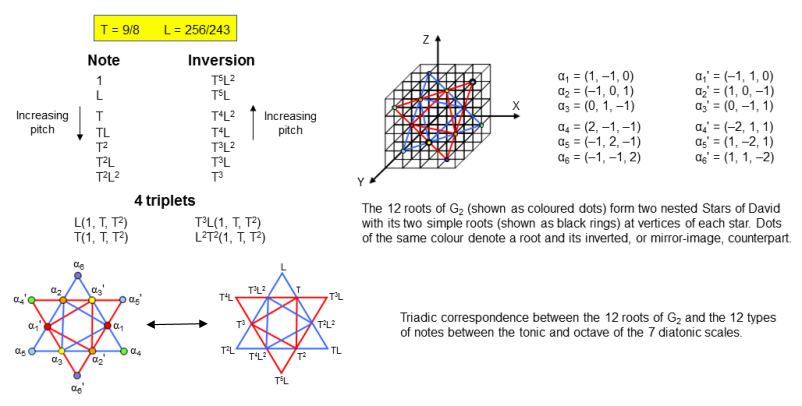
The 48 notes consist of the 12 basic notes found in the 7 types of diatonic scales and 36 repetitions of these notes. The table above shows that the notes with tone ratio 1024/729 and 729/512 occur only once in the 8 Church Modes. So there are only 10 notes that are repeated 36 times. The 12 basic notes correspond to the 12 roots of G2, the rank-2 exceptional subgroup of F4. The tonic and octave correspond to its two zero roots. G2 contains as subgroups the colour SU(3) and electro-weak symmetry group U(1)×SU(2) that form the basis of the Standard Model of particle physics. The 12 roots (αi, αi'; i = 1-6) form 4 SU(3) triplets shown below. Plotted in the X, Y, Z Cartesian coordinate system, they are located at the corners of 4 nested Stars of David as two triplets (α1, α2, α3) & (α4, α5, α6) and their two corresponding antitriplets (α1', α2', α3') & (α4', α5', α6'). Corresponding to them are 4 triplets of basic notes. They are written in the diagram in terms of the Pythagorean tone interval T = 9/8 and the leimma L = 256/243, whose counterpart in the modern equal-tempered scale is the semi-tone. Basic notes at diametrically opposite corners of a Star of David are inversions of each other. Their G2 root counterparts (denoted by circles of the same colour at the corners of red and blue triangles) are located at opposite points of Stars of David as mirror images of each other.
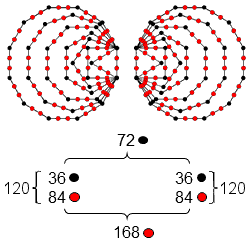
Each Mode has 27 intervals below the octave between its 8 notes, of which 6 intervals are those between the tonic and the next 6 notes and 21 are intervals between the last 7 notes. The total number of intervals for the 8 Modes = 8×27 = 216 = 8×(6+21) = 48 + 168, where "48" is the number of notes in the 8 Modes between the tonic & octave and "168" is the total number of intervals between their last 7 notes. This has a natural interpretation in terms of the 8×8 array of 64 hexagrams used in I Ching, the ancient Chinese system of divination, which was compared with the triacontagons on page 9. "48" is the number of lines & broken lines in the 8 diagonal hexagrams and "168" is the number of lines & broken lines in the 28 off-diagonal hexagrams on one side of the diagonal. So there are 216 lines & broken lines in a diagonal half of the array. The number of lines & broken lines in the whole array = 384 = 168 + 216 = 168 + 48 + 168. This has a musical interpretation in terms of the 48 notes between the tonic & octave (24 in each set of Modes, or, alternatively, 24 notes up to that with tone ratio 1024/529 and 24 notes higher than that), the 168 rising intervals & the 168 falling intervals. These compare with the two interior angles of 168° in two adjacent sectors and their diametrically opposed counterparts and with the pair of vertex angles of 24°:
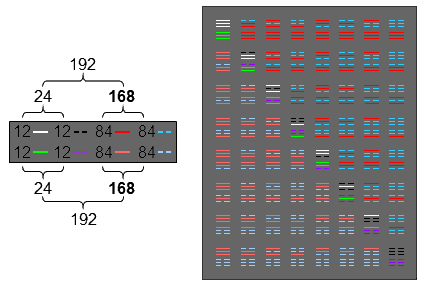 |
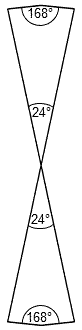 |
|
|
24:168 pattern of angles in two adjacent sectors of the triacontagon. |
This double 24:168 pattern conforms to the holistic pattern
384 = 192 + 192 = (24+168) + (24+168)
found in all sacred geometries (see The holistic pattern). It is further evidence of the holistic nature of the 421 polytope. 384 (= 244!) is the order of B4, the hyperoctahedral group in 4 dimensions (see here). This is the group of symmetries of the 4-cube. It has the subgroup B3, the hyperoctahedral group in 3 dimensions of order 233! = 48. This is the octahedral group of 24 rotations and 24 rotations+reflections. It is the group of symmetries of the octahedron and the 3-cube. B4 also has the hyperoctahedral subgroup D4 of order 192. This has the subgroup D3 in 3 dimensions that is of order 24. Comparing these properties with the 8 Church Modes, we see that
We are not claiming that these symmetry groups actually describe the 8 Modes. For the present purpose, it is sufficient to demonstrate the existence of numerical analogies between the Modes and these symmetries that imply the existence of a universal pattern because these correspondences are too detailed to be dismissed as due to coincidence. The following implications of the existence of this pattern are profound: 1. E8×E8 heterotic superstrings exist; 2. the UPA is such a superstring because its structure, paranormally described over a century ago by Annie Besant & C.W. Leadbeater, conforms to this pattern embodied in both sacred geometries and holistic systems, such as the Church Modes.
The tonic, octave & unit interval in the set of 30 intervals associated with each Mode correspond to the 3 successive corners of two adjacent sectors of each triacontagon whose interior angle is 168°. The (8×27=216) intervals below the octave between the notes in the 8 Modes correspond to the (8×27=216) remaining corners of the 8 triacontagons. The number 216 of Geburah, the 6th Sephirah of Construction, is a structural parameter of the inner Tree of Life, being the number of yods per set of 7 enfolded polygons that line the 88 sides of their 47 tetractyses:
|
|
| 216 yods per set of 7 enfolded polygons as the inner form of successive Trees of Life lie on the 88 sides of their 47 tetractyses. |
It is also the number of yods that either surround the centres of the first 6 separate polygons with 36 corners, themselves a holistic system (see Article 4), or line the boundaries of the first (6+6) separate polygons. 36 is the number value of ELOHA, the Godname of Geburah, whose gematria number value is 216.
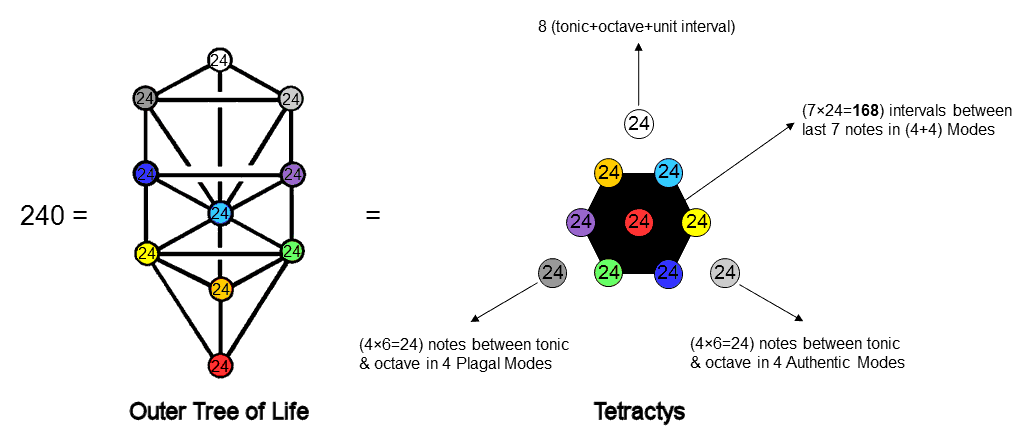
The tetractys is the Pythagorean representation of holistic systems. A tetractys array of the number 24 generates the interval composition of the (4+4) Modes:
 |
|
|
The 3 Sephiroth of the Supernal Triad determine the framework of the 8 scales, generating the 72 intervals that are either unit intervals or notes. Notice that the number 24 assigned to Chokmah is the number of notes between the tonic & octave of the 4 Authentic Modes and the number 24 assigned to Binah is the number of notes between the tonic & octave in the 4 Plagal Modes. The 7 Sephiroth of Construction determine the (7×24=168) intervals between the last 7 notes in the 8 Modes. The counterpart in the 1-tree of this 10-foldness in the number 240 is analysed on #37 of Wonders of Superstrings. It was found that the 240 yods needed to constructed the 1-tree from Type A triangles consist of 10 sets of 24 yods. The 72 yods in 3 sets form the so-called "root" & "trunk" of the 1-tree and the 168 remaining yods in 7 sets form its so-called "branches" (these terms are defined here). In the context of the 8 Modes, the 72 yods correspond to the 72 notes & unit intervals, whilst the 168 yods correspond to the 168 intervals between the their last 7 notes. It is appropriate that their notes should constitute the "trunk" (i.e., the core) of the 8 Modes and that the intervals between their last 7 notes should be thought of as their branches. #2 in Polychorons & Gosset polytope discusses the counterparts in other sacred geometries of the 10-foldness in the number 240. It could appear in the 8 triacontagons with 240 corners in two possible ways:
(the third and last possible factorisation: 30 = 2×15 cannot generate a global factor of 10 and must therefore be excluded from consideration).
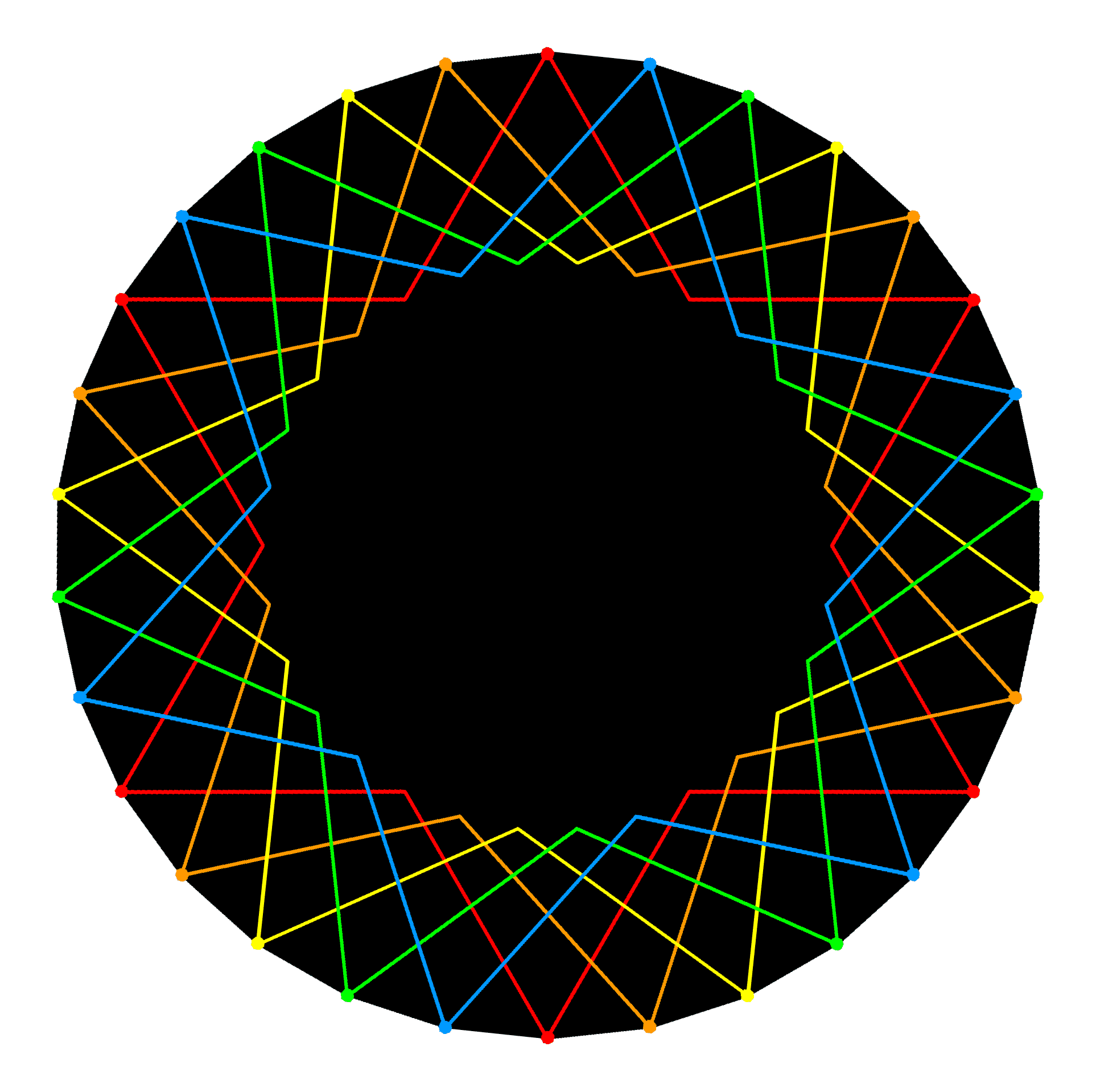
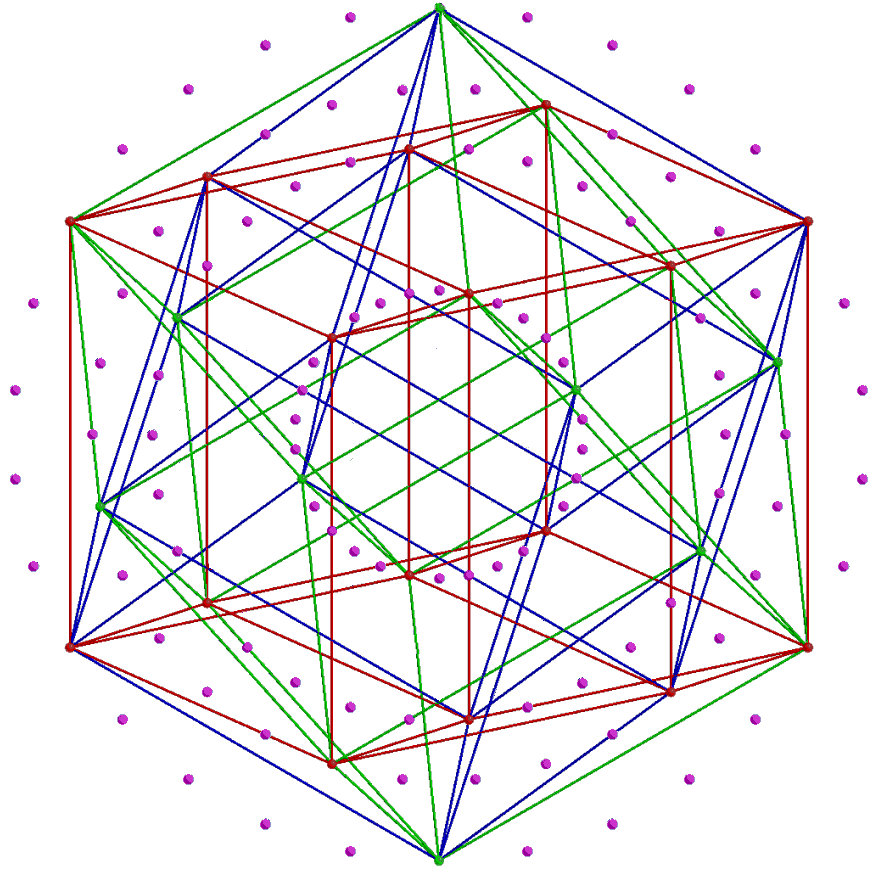
As pointed out in #2, each set of 4 triacontagons with 120 corners are the Coxeter plane projections of the 120 vertices of 5 24-cells that make up a 600-cell. This means that the (4+4) triacontagons are the projections of the 240 vertices of 10 24-cells, the Coxeter projection of the 421 polytope being that of a compound of two 600-cells. This in turn means that possibility 2 is the correct one, for the following picture shows that the 24 vertices of each 24-cell actually coincide with 6 corners of a hexagon/hexagram in each of the 4 triacontagons that are the Coxeter projection of the 120 vertices:
 |
 |
 |
|
|
|
The 24-cell. |
Therefore, 5 distinct 24-cells not sharing any vertices can be fitted in each 600-cell whose Coxeter plane projection is a set of 4 triacontagons. The factor of 10 is spread over all 8 triacontagons instead of originating in the dihedral symmetry group D10 that is one of the 7 subgroups of D30, the dihedral symmetry group of the triacontagon. But now it also exhibits the factorisation 2×5, not because D10 contains D5 as a subgroup but because the 8 triacontagons consist of two sets of 4 due to the Coxeter plane projection of the 421 polytope being a compound of two 600-cells. Having established that the 240 intervals between the notes in the 8 Modes comprise 8 sets of 30 intervals, let us see whether — as the analogy with the 8 triacontagons would suggest — they have the factorisation 2×5×24 as well. A given number of objects can, of course, be divided up any way we chose. But, unless they can form groups representing types or classes, these choices are not likely to be significant in the context of a supposed, archetypal pattern. As found above, the 30 intervals between the notes in a Mode comprise 6 notes between the tonic and the octave and 24 other intervals made up of the tonic, octave, unit interval and 21 intervals between the last 7 notes. The 4 Authentic Modes comprise 4 sets of 6 notes (i.e., a set of 24 notes) and 4 sets of 24 intervals. Hence, the 120 intervals between these notes comprise 5 sets of 24 intervals. Similarly for the 4 Plagal Modes. The 8 Modes comprise (5+5=10) s, respectively,ets of 24 intervals. This is analogous to the (5+5) 24-cells, each with 24 vertices, that are present in the compound of two 600-cells.
Now let us see whether the representation shown above of the number 240 as a tetractys array of 24s is more than just arithmetic, i.e., do the numbers 72 and 168, into which it splits, factorise, respectively, as 3×24 and 7×24 when they denote intervals? Let us denote classes of intervals by underlined numbers to distinguish them from numbers of classes. Let us use primes, double primes, etc to distinguish different sets of the same number of intervals. By definition:
72 = 2×4×(3 + 6)**,
where 3 = {tonic, octave, unit interval} and 6 = 6 notes between the tonic & octave. Hence,
72 = 8×{tonic, octave, unit interval} + 2×4×6
= 24' + 2×24,
where 24' = 8×3 and 24 = 4×6. The set of 72 intervals comprises 3 classes of 24 intervals. By definition:
168 = 2×4×21.
21 = 6' + 15,
where 6' = 6 intervals between the octave and the 6 notes and 15 = 15 intervals between the latter. The 6 notes may be represented by a dot at the centre of a pentagon whose corners denote the other 5 notes:
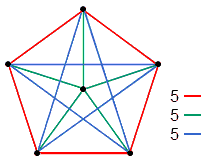 |
Three sets of 5 straight lines join the corners of a pentagon to its centre. If these points represent notes, the lines represent intervals between every pair of notes. There are 3 types of lines: red, green & blue. The intervals that correspond to them form 3 classes. |
The 15 straight lines joining all pairs of points denote the 15 intervals. They consist of 3 classes of 5 lines, coloured, red, green & blue. Similarly, the 15 intervals can be regarded as consisting of 3 different sets of 5 intervals: 5, 5' & 5''. Therefore,
15 = {5, 5', 5''}
and
168 = 2×4×(6'+15) = 2×4×6' + 2×4×{5, 5', 5''}
= 2×24'' + 5×{8, 8', 8''}
= 2×24'' + 5×24''',
where 24'' = 4×6' and 24''' = {8, 8', 8''}. (N.B. The 3 sets of 5 intervals can be re-arranged as 5 sets of 3 intervals; the subsets 8, 8' & 8'' are then intervals taken from all 8 Modes. As explained in the footnote for the general case, the expression "5×..." denotes not multiplication by a number, for the sets 24''' vary in content, but summation over all subsets of 5 intervals between the 6 notes between tonic & octave). We find that the 168 intervals between the last 7 notes in the 8 Modes comprise 7 classes of 24 intervals. Therefore, the (72+168=240) intervals actually comprise 10 classes of 24 intervals; the factorisation 240 = 10×24 is not merely arithmetic in the context of the 240 intervals. However, in this context it does not signify that the latter consist of 10 identical sets of 24 intervals. The sets are different and, as the footnote points out, the above equations are not meant to be understood as merely arithmetic identities but identities between sets, namely, classes of intervals. The analogy between the Modes and the 10 24-cells making up the compound of two 600-cells, whose Coxeter plane projection is the set of 8 concentric triacontagons, is now complete. One 600-cell with 120 vertices is the polytopic counterpart of 4 Authentic Modes with 120 intervals between their notes; the other 600-cell with 120 vertices is the counterpart of the 4 Plagal Modes with 120 intervals. The group-theoretical counterpart of this 72:168 division in intervals is the fact that the 240 roots of E8 consist of the 72 roots of its exceptional subgroup E6 and 168 other roots. It is displayed in one of the diagrams shown on this page.
* Article 64 discusses the properties and significance of these two sets of polygons
and their counterparts in other sacred geometries.
** In the analysis presented here, the term "N×n", where N is the
number of classes (denoted by n) of n intervals, is not to be understood in the normal, arithmetic sense as
N times (or multiplied by) the set n. This is because the equations should be read as expressing identities
between sets rather than equalities between sums of numbers. The term is shorthand
for addition (in the sense of set theory) of all members of all subsets ni of a given
set:
N
N×n ≡ ∑ ni,
i=1
where ni is one of the N subsets of n intervals, which differ in content according to the value of i. Similarly, for any term in an equation containing several factors, e.g., N×M×n, it should be read as the double summation over both N and M of the n intervals in the subset ni, not as N×M identical sets of n intervals.
| << Previous 1... 13 14 15 16 [17] Next >> |