Home

The (192+192) lines & broken lines of the 64 hexagrams symbolize the 192 rotations of the tesseract and its 192 rotations+reflections

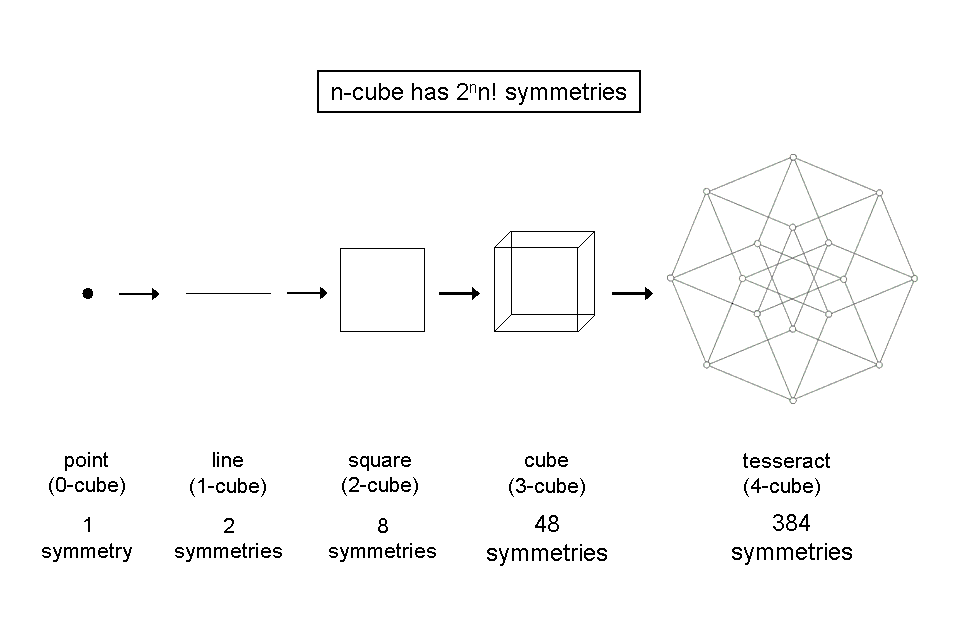
The point has one symmetry, namely, the reflection of it into itself in a mirror in which it is embedded. The straight line has two symmetries: it is unchanged by a rotation of 180° about an axis passing through its centre perpendicular to it and by a reflection in a mirror passing through its centre perpendicular to its length. The square has eight symmetries: four rotations of 0°, 90°, 180° & 270° and four reflections: two across its diagonals and two across vertical or horizontal lines passing through centres of opposite pairs of lines. The cube has 48 symmetries that define the octahedral symmetry group O_h. Its 24 proper rotations fall into four classes consisting of:

1. the identity, or rotation of 360°;
2. nine rotations of 90° (×3), 180° (×3) & 270° (×3) about axes passing through the centres of opposite faces;
3. six rotations of 180° about axes passing through the centres of opposite pairs of edges;
4. eight rotations of 120° (×4) & 240° (×4) about the four body diagonals.

The cube has also 24 proper rotations combined with reflections that leave it unchanged. The four-dimensional version of the cube (3-cube) is the 4-cube, or tesseract. It has 384 symmetries. The easiest way of seeing this is to note that each of its 16 vertices is the intersection of four edges, which can be permuted in (4!=24) ways, generating 24 independent orientation, so that there are (16×24=384) possible ways of changing the 4-cube.

The 384 symmetries* consist of 192 rotations and 192 combinations of rotations and reflections. Here are animated examples of its rigid rotations. The three-dimensional projections of the rotations of a tesseract can also be viewed here. The 192 rotations comprise the following rigid rotations in a plane:

1. 6 planes containing four 3-cube-centres and four face-centres, each with three rotations (90°, 180°, 270°), for a total of 18 rotations;
2. 24 planes containing two 3-cube-centres, two face-centres, and four edge-centres, each with one rotation (180°), for a total of 24 rotations;
3. 16 planes containing six face-centres, each with two rotations (120° and 240°), for a total of 32 rotations;
4. 12 planes containing four face-centres and four vertices, each with one rotation (180°), for a total of 12 rotations.

There are 105 rotations that act in more than one plane, that is, 104 rotations, apart from the inversion, in which the point (x₁, x₂, x₃, x₄) goes to (−x₁, −x₂, −x₃, −x₄). Together with the identity, there are 87 proper rotations in the 4-cube, which consists of 16 vertices (0-cubes), 32 edges (1-cubes), 24 squares (2-cubes) & 8 cubes (3-cubes), i.e., 80 0-, 1-, 2- & 3-cubes.  87 is the number value of Levanah, the Mundane Chakra of Yesod, and 80 is the number value of this Sephirah. If one is willing to make the reasonable judgement that the appearance of two numbers associated with the same Sephirah is not a matter of coincidence, it indicates that the tesseract is a holistic system, its 384 symmetries being symbolized by the 384 lines & broken lines in the 64 hexagrams of the I Ching table. The 48 lines & broken lines in its diagonal would then symbolize the 48 symmetries of a cube, namely, the octahedral symmetries of O_h, the 24 lines & broken lines in the eight upper trigrams in the diagonal denoting its 24 rigid rotations and the 24 lines & broken lines in the eight lower, diagonal trigrams denoting its 24 rotations/reflections. The seven off-diagonal copies of the 24 lines & broken lines in the eight diagonal trigrams would refer to the 168 rotations of the seven copies of the 3-cube (its "cells") that extend in the fourth dimension of space.

What is the significance of the 4-cube for superstrings? Hypercubes can fill 4-space, just as cubes can be stacked to fill 3-space. According to E₈×E₈ heterotic superstring theory, two 10-dimensional space-time sheets are separated by a finite gap extending along the tenth dimension of space predicted by supergravity theories. It suggests that 3-space might be a cross-section of a 4-space tessellated across this gap with tesseracts. If so, the eight diagonal hexagrams of the I Ching table would represent the octahedral symmetry O_h of cubes filling ordinary space and the 56 off-diagonal hexagrams would represent the extra 336 symmetries of hypercubes filling 4-dimensional space that are hidden from physical awareness because they refer to a dimension of space that normal cognition is not programmed to detect, namely, the seven cubic cells (3-cubes) of a tesseract that surround its central cube. Perhaps Charles Hinton was right after all when he proposed in his book A New Era of Thought (1888) that space has four dimensions (see here)....

It is, of course, not just the 64 hexagrams that symbolize the tesseract because, as this website proves, all sacred geometries embody the universal patterns:

384 = 192 + 192,

192 = 24 + 168,

and

384 = 48 + 336

(see here). Nor, in view of remarks made in the footnote, is the 4-cube the only 4-polytope that possesses 384 symmetries. So does the 24-cell, which plays a central role in the geometry of the 4₂₁ polytope discussed in 4-d sacred geometries. Here is the reason why it embodies this global parameter of holistic systems.

* This is the hyperoctahedral group BC₄ of 384 symmetries possessed by the tesseract and two other 4-dimensional, regular polytopes called the "16-cell" (the dual of the tesseract) and the "24-cell," which is self-dual. See here. The 192 symmetries are those of the hyperoctahedral group D₄, a subgroup of BC₄. The demitesseract, the 4-dimensional version of demihypercubes, has 192 symmetries (see here). D₄ contains the tetrahedral group T_d with symmetry order 24. The 192 symmetries are symbolised by the 192 lines & broken lines in each diagonal half of the 8×8 matrix array of 64 hexagrams, the 24 lines & broken lines in the eight diagonal trigrams in each half symbolising the 24 symmetries of T_d. The I Ching table represents the 384 symmetries of the tesseract, the 192 symmetries of the demitesseract, the 48 symmetries of the octahedral group and the 24 symmetries of the tetrahedral group.

Home