ARTICLE 14
.
by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: www.smphillips.mysite.com
Abstract
The musical modes of ancient Greece considerably influenced the early development of Western music. Their status, however, is not merely historical, as most music scholars now think. This article will demonstrate their sacred nature as the musical counterpart of the cosmic blueprint called the ‘Tree of Life’ at the heart of Jewish mysticism. Mathematically speaking, the Hypolydian mode is the perfect mode because it alone contains all the notes of the Pythagorean scale, thereby exhibiting the maximum possible harmony of their mathematical proportions. The triadic structure of this musical scale is paralleled in the modes themselves, both showing this pattern because they are in one-to-one correspondence with the seven Sephiroth of Construction of the Tree of Life, which bear a similar relationship to one another. The correspondence explains the unique status of the Hypolydian mode, which occupies the middle ground of the seven modes because it corresponds to Tiphareth at the centre of the Tree of Life. Godnames assigned to various Sephiroth are shown to define the tonal composition of the seven modes. This provides evidence of their sacred character in that their patterns of notes conform to the universal paradigm of the Tree of Life and so are defined by the mathematical archetypes embodied in the Divine Names. The striking role played by the number 4, the Pythagorean Tetrad, in expressing the tonal composition of the Greek modes provides confirmation of their sacred status. Although music is said to be the language of the soul, only that based upon these modes and played with instruments tuned to them can be said to be its true idiom, as both are structured in analogous ways: only like can sympathetically respond to like.
1
1. The seven ancient Greek musical modes
According to ancient Greek thinking, man had descended from the Gods. Today, evolution is perceived, if one is religious, as proceeding inwardly from the material to the spiritual world or, according to Darwinian biology, as traversing the planet from one species to another by accident and without purpose. The ancient Greeks, instead, saw the world and its inhabitants as having descended from the divine to the human level. This fundamental difference in how they saw their place in the universe was reflected in the way they regarded the musical scale. Instead of considering the notes of the major scale: do, re, mi, fa, sol, la, ti, do as ascending in pitch, as musicians do now, the Greeks thought in terms of a descending scale, with its eight notes divided into two sets of four notes, or ‘tetrachords.’ The most important note in a scale was the mesē , or middle note, which was the highest note of the lower tetrachord.* It set the quality of music played according to a particular scale because it was often the most played of the notes. The Pythagoreans compared its position to that of the sun amidst the planets: it held the melody together as its fulcrum. Altering the sequence of whole tones and semitones within a tetrachord generated different scales. Seven distinct scales or modes came to be eventually recognised and used in church music, although this is a simplification, as variations of these were known: They are called the Dorian, Hypodorian, Phrygian, Hypophrygian, Lydian, Hypolydian and Mixolydian modes. They were named not after their first or last notes (being sequences of descending notes, tonics within these scales were not definable) but after the various people who preferred one mode to another, depending on their character and temperament. Ancient Greeks were very familiar with the distinct qualities of melodies played according to some of these modes and the psychological effects they had on those listening to them. The following story illustrates this: according to Iamblichus, one of his biographers (1), Pythagoras devised melodies to heal the soul by soothing its passions and cleansing it of negative conditions such as sorrow, rage, pity and anger. He would play this music to his disciples as they prepared for bed in order to remove all the emotional disturbances they had acquired during the course of the day. When they woke up the next morning, Pythagoras freed them from the heaviness and torpor of their sleep by certain kinds of singing and playing of the lyre. Iamblichus tells the story of how a young man, angered by seeing his girl-friend leave the house of his rival, had eaten and drunk all night, his jealousy inflamed by a piper playing Phrygian music, which made him unable to resist his impulses. Pythagoras persuaded the piper to play slow and heavy spondaic music probably of the Dorian mode, which had the effect of restraining and calming the man (2), who returned home in a sober and orderly fashion. Whether this tale is true or not (and one must bear in mind that Iamblichus was wont to glorify his hero by passing off as factual all the legends surrounding him), it serves to illustrate the belief in ancient Greece that music based upon their musical modes could transform the behaviour of the hearer in positive or negative directions; the music of some modes was thought to be character-building, whilst that of others led it astray.
Plato had strong views about the rightness and wrongness of the various modes. In his Republic, which sets out his ideas about an ideal society, he advocated only the Dorian and Phrygian modes. He regarded the “mixed Lydian” and “the ‘tight’ Lydian” as “wailing modes” suitable for women and thought that the Ionian and “slack” Lydian encouraged “drunkenness, softness, and idleness,” although he probably also meant his words to be a joke for his readers because certain strings were “tight” for some modes and “slack” for
_______________________
*The mesē originally referred to the middle string of the seven-stringed lyre. It came later to denote the fourth lowest note of a musical scale.2
others. He meant the word ‘tight’ to indicate that the mode reached into higher notes that put a strain on the voice and altered its quality; in the slack Lydian mode the melody stayed more in the lower part of the octave. Plato makes Socrates remark: “Just leave that mode which would appropriately imitate the sounds and accents of a man who is courageous in warlike deeds and every violent work, and who in failure or when going to face wounds or death or falling into some other disaster, in the face of all these things stands up firmly and patiently against chance. And, again, leave another mode for a man who performs a peaceful deed, one that is not violent but voluntary, either persuading someone of something and making a request — whether a god by prayer or a human being by instruction and exhortation — or, on the contrary, holding himself in check for someone else who makes a request or instructs him or persuades him to change, and as a result acting intelligently, not behaving arrogantly, but in all these things acting moderately and in measure and being content with the consequences. These two modes — a violent one and a voluntary one, which will produce the finest imitation of the sounds of unfortunate and fortunate, moderate and courageous men — leave these” (3). The modes referred to here are the Phrygian and Dorian. Aristotle (4) declared Socrates to have been wrong in including the Phrygian mode for an ideal state, for the exciting, emotional quality of its melodies made it apt for Bacchic celebrations. Plato might have been expected to deprecate this aspect but, surprisingly, he ignored it. Perhaps the Phrygian mode had other qualities that he esteemed sufficiently not to reject it. More likely, however, there was a variety of Phrygian modes, not all of which were associated with orgiastic cults, and one of them met Plato’s approval.
One of the most widely used modes in the fifth century and probably earlier, the Dorian was always well regarded. It was a versatile mode, often employed for choral song but not confined to it, and compatible with more than one mood. On the whole, however, it was regarded as dignified and manly. Aristotle said that “everyone agrees that it is the steadiest and the one that most has a manly character” (5). It is mentioned in The Hymns of Orpheus, a great poetic work of ancient Greece:
“‘Tis thine all Nature’s music to inspire, With various-sounding, harmonising lyre; Now the last string thou tun’st to sweet accord, Divinely warbling now the highest chord; Th’immortal golden lyre, now touch’d by thee, Responsive yields a Dorian melody.” (6)
Plato wanted to eliminate from his ideal society the Lydian mode as emotional, fit only for tragedy, as was deemed the Mixolydian. Indeed, Sophocles introduced it to his plays for this very reason. However, in his book Music in Ancient Greece and Rome, Landels remarked: “One suspects that Plato is being a bit puritanical here, as the Mixolydian is described elsewhere as combining (hence the prefix Mixo-) the emotional quality of the Lydian with the nobility of the Dorian, and therefore being suitable for tragedy” (7).
The Hypodorian and Hypophrygian modes were not identified under these names before the late fifth or early fourth century. The music scholar M.L. West conjectured (8) that the Hypolydian was an invention of Eratocles, who enumerated the seven species of the octave in one genus, devising the name for the sake of parallelism, so that Lydian, Phrygian and Dorian each had a corresponding Hypo- species starting on the note a fourth higher in the scale. There were several rival schemes of classification, with general agreement only on the sequence: Dorian, Phrygian and Lydian. As will be discussed in the next section, the confusion caused Aristoxenus to base modal scales on keys rather than consider them as octave species, using the seven names that Eratocles had applied
3
to his octave species. This purely musical emphasis prevailed, with the consequence that the mathematical nature of the unfolding of the modes ceased to be of interest to anyone. Music had passed out of the hands of mathematicians and philosophers looking for divine design (and perhaps divine inspiration) in music and had become the practical business of musicians more concerned with how to tune their instruments properly so as to play music that just entertained, rather than melodies that could heal and elevate the soul.
In antiquity there seems to have been general agreement on the sequence: Dorian, Phrygian, Lydian, but only partial agreement about others. This caused Aristoxenus to disregard the Pythagorean basis of the musical scale by adhering to the simple rule that a fourth is 2½ tones and that all intervals must be measured in tones and fractions of a tone. For some years a pupil of Aristotle, Aristoxenus no doubt shared his teacher’s rejection of Pythagorean principles in general and the Pythagorean basis of music in particular. He worked out a system of melodic scales based not on modalities but on keys — thirteen of them in fact, arranged at regular semitone intervals over a whole octave. He did not refer to the seven species of scale by their modal names, although he adopted existing nomenclature to name them. Aristoxenus added an eighth scale above the Mixolydian to complete the octave, calling it the Hypomixolydian. Later, his system was reformed to that of a 15-key system. Both were criticised eventually (although to no avail, as the latter had already become firmly established) by the musical theorist Ptolemy, who condemned the completion of the octave with the Hypomixolydian as mere duplication.
2. Triadic structure of the Pythagorean scale
Historically speaking, musical scales were always divided into eight notes because the ancient Greeks regarded them as composed of two tetrachords. If the pitch, or ‘tone ratio,’ of the starting note (‘tonic’) of a scale is given the value of 1, the eighth note of the scale (‘octave’) has a tone ratio of 2, that is, it has twice the frequency of the tonic and is the tonic of the next higher set of eight notes. The arithmetic mean of these two frequencies is (1+2)/2 = 3/2. This is the tone ratio of the ‘perfect fifth,’ so-called because it is the fifth note in the ascending scale, counting from the tonic. The musical scale based entirely on octaves and fifths is called the ‘diatonic scale.’ The tone ratios of the eight notes making up an octave of this scale are:
1 9/8 (9/8)2 4/3 3/2 27/16 243/128 2
The diatonic scale is also called the ‘Pythagorean scale' because Pythagoras is generally thought to have discovered its mathematical basis. It comprises five tone intervals of 9/8 and two intervals of 256/243, called in Greek the leimma, or ‘left over,’ which corresponds to the modern semi-tone, although slightly less than it. Its tone interval structure is:
tone–tone–leimma–tone–tone–tone–leimma.
Below is given proof that the six notes D, E, F, G, A & B of the Pythagorean scale above the tonic C form only two chords of three notes with the same relative proportions of their tone ratios:
D
E
F
G
A
B1. D:E:F G:A:B 9/8:(9/8)2 :4/3 (= 1:9/8:32/27) ≠3/2:27/16:243/128 (= 1:9/8:81/64);
2. D:E:G F:A:B 9/8:(9/8)2 :3/2 (= 1:9/8:4/3) ≠ 4/3:27/16:243/128 (= 1:81/64:729/512);
3. D:E:A F:G:B 9/8:(9/8)2 :27/16 (= 1:9/8:3/2) ≠ 4/3:3/2:243/128 (= 1:9/8:729/512);4
4. D:E:B F:G:A 9/8:(9/8)2 :243/128 (= 1:9/8:27/16) ≠ 4/3:3/2:27/16 (= 1:9/8:81/64);
5. D:F:G E:A:B 9/8:4/3:3/2 (= 1:32/27:4/3) ≠ (9/8)2:27/16:243/128 (= 1:4/3:3/2);
6. D:F:A E:G:B 9/8:4/3:27/16 (= 1:32/27:3/2) = (9/8)2:3/2:243/128 (= 1:32/27:3/2);
7. D:F:B E:G:A 9/8:4/3:243/128 (= 1:32/27:27/16) ≠ (9/8)2:3/2:27/16 (= 1:32/27:4/3);
8. D:G:A E:F:B 9/8:3/2:27/16 (= 1:4/3:3/2) ≠ (9/8)2:4/3:243/128 (= 1:256/243:3/2);
9. D:G:B E:F:A 9/8:3/2:243/128 (= 1:4/3:27/16) ≠ (9/8)2:4/3:27/16 (= 1:256/243:4/3);
10. D:A:B E:F:G 9/8:27/16:243/128 (= 1:3/2:27/16) ≠ (9/8)2:4/3:3/2 (= 1:256/243:32/27).Only the chords DFA and EGB listed in the highlighted case 6 made up of alternate notes and spanning the interval of a perfect fifth exhibit the same proportions 1:32/27:3/2 of their tone ratios, their corresponding notes being each separated by a whole tone interval. Notice that the six notes above the tonic form ten possible pairs of chords of three notes, i.e., 20 chords. Musical harmony between a pair of chords exists in this sense only for one of the ten pairs. All seven notes form 7C3 = 35* chords of three notes, that is, (35–20=15) more chords than the six notes above the tonic. The number value 15 (9) of the Godname YAH is therefore the number of chords of three notes that include the tonic.
The chord EGB is the chord DFA lifted by a whole tone interval (Fig. 1).
__________________________
*nCr is the number of combinations of n objects, taken r at a time. nCr ≡ n!/r!(n-r)!, where n! = 1×2×3×… n.5
According to Kabbalah, there are seven ‘Divine Qualities’ that manifest in an objective sense. They are the seven Sephiroth of Construction: Chesed, Geburah, Tiphareth, Netzach, Hod, Yesod and Malkuth, They are symbolised by circles or spheres in the representation of Adam Kadmon, or ‘Heavenly Man,’ called in Kabbalah the ‘Tree of Life’ (Fig. 2). The six Sephiroth of Construction above Malkuth, the lowest Sephirah of the Tree of Life, form two triads: Chesed–Geburah–Tiphareth and Netzach–Hod–Yesod. They are the reflections of the Supernal Triad of Kether, Chokmah and Binah in Beriah (World of Creation) and Yetzirah (World of Formation). Each triad represents a three-fold cycle of active outflow, returning inflow and the static equilibrium resulting from these two opposing currents of activity.
As stages in this triple cycle, Netzach corresponds to Chesed, Hod corresponds to Geburah and Yesod corresponds to Tiphareth. The Tree of Life and the tetractys at the centre of Pythagorean philosophy are equivalent symbols of the ten-fold nature of Divine Unity. Fig. 3 exhibits their equivalence. The first triad (indicated by the blue triangle in Fig. 4) corresponds to the triad of notes B, E & G.
The second triad (indicated by the red triangle) corresponds to the triad of notes A, D & F. The seventh note, B, of the ascending scale is the first note of the descending scale below the octave. As such, it has to correspond to Chesed, the first Sephirah of Construction to be emanated. This means that the note A, its counterpart in the other triad, has to correspond to Netzach, which is the counterpart of Chesed in the second triad. G, the perfect fifth, which is the arithmetic mean of the tonic and octave and the mesē of the Pythagorean scale, corresponds appropriately to Tiphareth, the centre of the Tree of Life in both a geometrical and a metaphysical sense. This means that note E, the last note of the first triad, has to correspond to Geburah, the remaining member of the first triad of Sephiroth of Construction, so that its counterpart, note D, has to correspond to Hod, the counterpart of Geburah in the second triad. The tonic C corresponds to the yod at the centre of the tetractys because the latter symbolises Malkuth, the last of the seven Sephiroth of Construction, just as the tonic of a descending scale is the last of the seven notes belonging to that scale. The seven notes of the Pythagorean scale* bear a formal
__________________________
* Only the tone ratios of the Pythagorean scale possess this triadic relationship.6
correspondence to the qualities of the Sephiroth of Construction as they manifest in the material, psychological and spiritual make-up of human beings, as well as, cosmically speaking, in their corresponding Mundane Chakras, as will now be explained.
Just as the six Sephiroth of Construction above Malkuth consist of two matching triads, so the six notes above the tonic form uniquely two harmonious chords. This illustrates the parallel between the elements of musical sound and the modes of being or awareness corresponding to these Sephiroth that exist at conscious and superconscious levels within man, for both are seven-fold, having the same 1:3:3 pattern, as now explained. His sensory experience generated by his outer, physical form is the Malkuth level (‘1’ in the pattern above), corresponding to the tonic, the musical starting point. His inner being encompasses the three levels (the first ‘3’ in the pattern) of personality (Yesod), mind (Hod) and spiritual perception (Netzach), the lattermost being what Theosophists call the principle of ‘Buddhi’ and what the ancient Greeks called ‘Psyche.’ Transpersonal levels express the next three Sephiroth of Construction (the next ‘3’), starting with the Christ level (Tiphareth), the reflection of “Our Father, who art in Heaven,” which corresponds to the Theosophists’ atmic plane, going next to the level of the spiritual monad (Geburah) on the Theosophical anupadaka plane and finishing with the seventh level of God as Divine Love (Chesed), corresponding to the Theosophists’ Adi, or Divine, Plane. This triad is the highest soul, called “Neshamah” in Kabbalah. As Plato said in his Timaeus, the mathematics of music reflects the nature of the World Soul, the divine prototype
7
according to which the human species is designed. The uppermost three levels are the transpersonal, immortal counterparts of the three levels of the temporary human soul that is subject to the law of karma during its incarnation. Similarly, the chord EGB is the counterpart of the chord DFA, one interval higher. Section 4 will show that the six Greek modes after the Lydian likewise uniquely consist of two sets of three that are harmonious counterparts of each other and separated by one interval. This correspondence will enable the seven modes to be correlated with the seven Sephiroth of Construction so that the traditional psycho-spiritual qualities of their music discussed in Section 1 can be compared with the way these Sephiroth find expression in human awareness.
3. The tone ratios of the Church musical modes
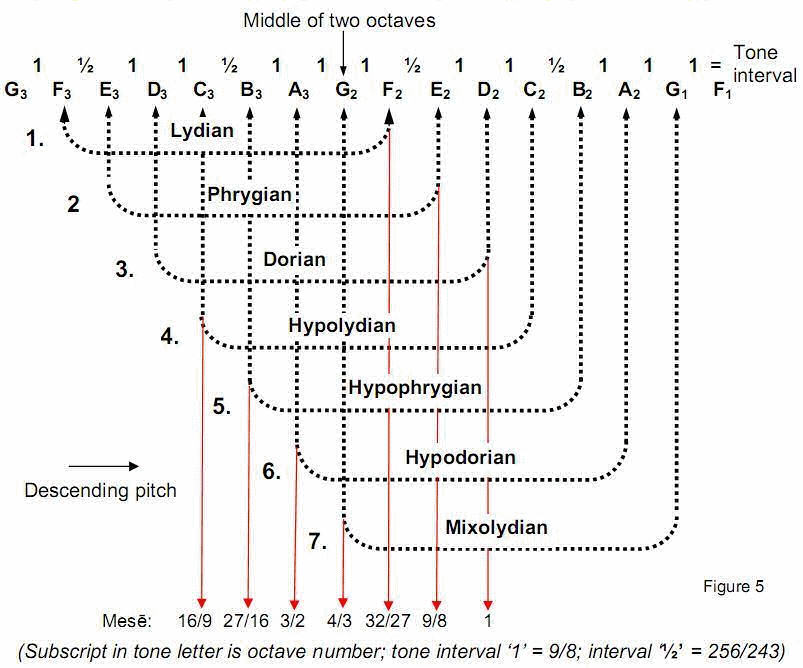
Let the tonic G1 of the Mixolydian mode be 1. The tone ratios of the 15 notes from G1 to G3 , the second octave of this mode, are:
The Pythagorean integers 1, 2, 3 & 4, which define the tonic, octave and their arithmetic and harmonic means — the perfect fifth and fourth — are the values of the whole number tone ratios present in these two octaves (written above in red). Starting with G1, selecting from right to left successive octaves and dividing their tone ratios by that of their associated tonic generates the table of tones ratios for each mode shown below:
Table 1. Tone ratios of the seven musical modes.
Lydian 1 9/8
81/64 729/512 3/2 27/16 243/128 2 Phrygian 1 256/243
32/27 4/3 3/2 128/81 16//9 2 Dorian 1 9/8 32/27 4/3 3/2 27/16 16//9 2 Hypolydian 1 9/8 81/64 4/3 3/2 27/16 243/128 2 Hypophrygian 1 256/243 32/27 4/3 1024/729 128/81 16//9 2 Hypodorian 1 9/8 32/27 4/3 3/2 128/81 16//9 2 Mixolydian 1 9/8 81/64 4/3 3/2 27/16 16//9 2 The reason for associating Greek modes with particular rainbow colours will be explained in Section 5. White cells contain tone ratios not belonging to any octave of the Pythagorean scale. Table 1 shows that the Hypolydian mode is unique in that it encompasses all the notes of the Pythagorean scale (no white cells). Table 2 shows the number of notes in each mode that differ from those in the Pythagorean scale:
Table 2
Mode
Lydian Phrygian Dorian Hypolydian Hypophrygian Hypodorian Mixolydian There are 16 (=42) such tone ratios. The (7×7=49) notes of the seven octaves comprise (49–16=33) Pythagorean tone ratios, of which seven are ‘1’s, leaving (33–7=26) such tone ratios other than 1. 26 is the sum of the number of combinations of ten objects A, B,
8
C, etc arranged in the four rows of a tetractys and 33 is the total number of their permutations:
B C
D E F
G H I JThe presence of these two numbers in the context of the seven Greek musical modes is no coincidence but reflects the fact that Plato’s Lambda tetractys of musical proportions generates all the Pythagorean tone ratios of the modes (see Articles 12 & 13). Indeed, those tone ratios other than 1 that occur more than once themselves form a tetractys:
9/8
81/64 4/3
3/2 27/16 243/128
256/243 32/27 128/81 16/9.The six tones above the tonic of the Hypolydian mode occupy the first three rows of this tetractys and the four non-Pythagorean tone ratios that occur more than once above the tonics of four other modes occupy its fourth row (notice how the Pythagorean Tetrad (4) defines these properties). It was pointed out in Article 12 that, counting from the tonic of the first octave, the 33rd note is 24, which is both the tenth overtone, counting from 2 (the first overtone) and the 26th note from 2, that is to say, the note 24 is prescribed by YAHWEH as having physical significance because 26 is the number value of this Godname of Chokmah. Article 13 discussed the relevance of the number 24 to both string theory and the connection between the Pythagorean theory of music and superstring physics.
The distribution of the numbers of Pythagorean tone ratios other than 1 in the seven modes is shown below:
Not only is the number value 26 of the Godname YAHWEH equal to the total number of these tone ratios but also the individual letter values of YHVH denote the numbers of Pythagorean notes found in individual modes, Y = 10 denoting the number found in the Phrygian, Hypophrygian, Dorian & Hypodorian modes. This demonstrates in a clear way the sacred character of the Greek musical modes, for the creative, archetypal Godname of YAHWEH, the most well-known of the Godnames, measures how many notes of the Pythagorean scale they possess. Its older version, YAH (YH), prescribes the seven modes because its number value 15 is the number of notes in the two octaves G1 to G3. It
9
also prescribes the five imperfect modes up to the Lydian because they have 15 non-Pythagorean notes. The significance of this will become apparent in Section 5. The Godname EL ChAI prescribes the seven modes because its number value 49 is the number of notes that they possess, notwithstanding that some of these have the same tone ratios. If the tonics have different pitches, then the seven modes will have 49 notes, all with different pitches. The Godname assigned to Yesod, meaning ‘foundation,’ therefore measures the foundation or basis of the seven modes. The Godname ELOHIM prescribes the modes because its number value 50 is the total number of notes involved in their generation from the second octave G3 of the Mixolydian mode (see Fig. 5). The Godname ELOHA with number value 36 defines the (6×6=36) notes above the tonics of the six imperfect modes. The Godname EHYEH with number value 21 defines the 21 of these notes that are Pythagorean (see Table 1). The letter values of AHIH are: A = 1 (the single Pythagorean note of the Hypophrygian), H = 5 (the five Pythagorean notes of the Mixolydian), I = 10 (the ten Pythagorean notes of the Dorian and Hypolydian) and H = 5 (the five Pythagorean notes of the Phrygian and Hypodorian). In a case where all the descending modes start and therefore finish on the same note (the tonic), the 49 notes become (7×6 + 1 = 43) notes, where 43 is the 21st odd integer after 1. Here, then, is clear evidence for the sacred nature of the seven Greek musical modes: the Hebrew Godnames of five Sephiroth define their mathematical characteristics. A sceptic who is inclined to dismiss this as coincidence must ask himself if it is plausible, given that the letter value of the Godnames have significance as well!
The even integers 2 and 4 and the odd integers 1, 3 and 5 measure the deviation of the six non-Pythagorean modes from the perfection of the Hypolydian because they are the numbers of tone ratios not belonging to this scale (Fig. 6).
Notice how, starting from the Hypophrygian mode, the most imperfect mode with five non-Pythagorean notes, there is an oscillation between modes with even and odd numbers of such notes as they develop into the perfect Hypolydian mode with no non-Pythagorean notes.
Although, according to Table 1, both the Hypodorian and the Mixolydian modes contain
(Schematic only. Notes on the same row do not necessarily have the same pitch)
10
the same number of Pythagorean notes, it can be argued that the latter is less perfect than the former because it does not contain a perfect fourth. It is for this reason that the Mixolydian, rather than the Lydian, mode is shown in Fig. 6 as the penultimate stage in the cycle of completion of the perfect (Hypolydian) scale, the Pythagorean (C) scale.
4. Tetrad Principle defines the musical modes
Fig. 7 shows how the Pythagorean character of the modes increases as they converge to the perfect Hypolydian mode. The ancient Greeks regarded all scales, firstly, as descending and, secondly, as composed of two tetrachords of four notes, their mesē being the highest note of the second tetrachord. Fig. 7 indicates that the first tetrachord of the Hypophrygian, Hypodorian, Mixolydian & Hypolydian modes comprise, respectively, 1, 2, 3 & 4 notes of the Pythagorean scale (shown encompassed by the grey triangle). The geometric symbol of Divine Wholeness — the tetractys, which symbolises these integers, therefore expresses the progression of musical modes to their perfection in the fourth, the Hypolydian mode. This is an example of what the author has called the ‘Tetrad Principle’ (10), whereby an infinite sequence of a class of mathematical objects finds its completion and perfection in its fourth member, which means that it always embodies a number characterising the cosmos in some way. Here, the Tetrad Principle determines the Pythagorean scale — the original basis of music itself (or, at least, Western music) — as the fourth of the musical modes. Another example of this principle at work prescribing the arithmetic properties of the seven modes is that the (7×8=56) notes of the seven octave scales (7 = 4th odd integer, 8 = 4th even integer) contain (42 =16) non-Pythagorean notes and (56–16=40) Pythagorean notes, where
40 =
4 4
4 4 4
4 4 4 4.When their tonics (and therefore octaves) coincide, the 56 notes become (1 + 7×6 + 1 = 44) notes, showing how the Pythagorean Tetrad, 4, aptly expresses the number of notes in the seven modes when they start and end on the same notes. Some of these notes, of course, will then be the same. But this does not invalidate the fact that there are 44 musical elements in seven such modes. Of these, 16 are non-Pythagorean, leaving (44–16=28) musical elements that are Pythagorean, where
28 = 1 + 2 + 3 + 4 + 5 + 6 + 7 = 1 + 2 + 4 + 7 + 14
is the second perfect number.* Also, 28 = 4×7, where 7 = 4th odd integer. The modes with the same tonic have 43 notes other than their common octave. This is the number of yods in a heptagon divided into tetractyses (Fig. 8). The yod at its centre shared by the seven tetractyses symbolises the tonic common to all seven modes and the six yods per tetractys denote the six other tones of each mode. Finally, as illustration of the Tetrad Principle, notice that the seven modes descend from G3, the second octave of the Mixolydian mode, which has the tone ratio 4.
____________________________
* A perfect number is one that is the sum of its factors. 1, 2, 4, 7 & 14 are the factors of 28.11
This provides new insight into the generalisation of the Platonic Lambda tetractys discussed in Articles 11 & 12, in which the tetractys of musical proportions generating all the octaves of the Pythagorean scale is but one face of a tetrahedron (Fig. 9) whose fourth face generates the octaves and their perfect fourths and perfect fifths in a symmetrical way.
The musical proportions at the centres of its faces are 6, 8, 12 and 24. 6 is the musical proportion of the tonic of the Pythagorean scale, whose mathematical structure is determined by the equation of proportion between its tonic, perfect fourth, perfect fifth and octave known to every student of music:
6:8 :: 9:12.
Relative to the tonic, the musical proportion 24 represents the second octave with tone ratio 4. In other words, this tetrahedron defines through its first and last face the two octaves with 15 notes spanned by the seven types of musical modes. In accordance with the Tetrad Principle, it is the fourth face of the tetrahedron whose central number defines two octaves that have great musical significance. In fact, 15 is the total number of ways of grouping four objects either singly, in pairs, in groups of three or as a group of four:
4C1 + 4C2 + 4C3 + 4C4 = 4 + 4 + 6 + 1 = 15.
The tetrahedron of musical proportions can thus be said not only to generate the notes of the Pythagorean scale but also to define in potentia the seven modes themselves.
5. Triadic structure of modes Phrygian–Mixolydian
In order of ascending pitch, taking the mesē D2 of the Mixolydian mode as 1, the mesēs of the seven modes are:
1 9/8 32/27 4/3 3/2 27/16 16/9
(see Fig. 5), that is, they form the Dorian mode. Its mesē is that of the Hypolydian mode (Pythagorean scale) — a perfect fourth. Taking the tonic of the Mixolydian mode (the lowest note) as 1, the mesēs of the six descending modes after the Lydian mode are:
81/32 9/4 2 16/9 27/16 3/2.
For convenience, the values of these meses will be labelled a, b, c, etc:
There are ten ways that mesēs a–f can be grouped in two distinct sets of three that preserve the order of their decreasing tone ratios:
12
1.
2.
3.
4.
5.a b c
a b d
a b e
a b f
a c dd e f
c e f
c d f
c d e
b e f6.
7.
8.
9.
10.a c e
a c f
b c d
b c e
b c fb d f
b d e
a e f
a d f
a d eThe relative proportions of their tone ratios are:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.a:b:c
a:b:d
a:b:e
a:b:f
a:c:d
a:c:e
a:c:f
b:c:d
b:c:e
b:c:fd:e:f
c:e:f
c:d:f
c:d:e
b:e:f
b:d:f
b:d:e
a:e:f
a:d:f
a:d:e81/32:9/4:2 (= 1:8/9:64/81) ≠ 16/9:27/16:3/2 (= 1:243/256:27/32);
81/32:9/4:16/9 (= 1:8/9:512/729) ≠ 2:27/16:3/2 (= 1:27/32:3/4);
81/32:9/4:27/16 (= 1:8/9:2/3) ≠ 2:16/9:3/2 (= 1:8/9:3/4);
81/32:9/4:3/2 (= 1:8/9:16/27) ≠ 2:16/9:27/16 (= 1:8/9:27/32);
81/32:2:16/9 (= 1:64/81:512/729) ≠ 9/4:27/16:3/2 (= 1:3/2:2/3);
81/32:2:27/16 (= 1:64/81:2/3) = 9/4:16/9:3/2 (= 1: 64/81:2/3);
81/32:2:3/2 (= 1:64/81:16/27) ≠ 9/4:16/9:27/16 (= 1:64/81:3/4);
9/4:2:16/9 (= 1:8/9:64/81) ≠ 81/32:27/16:3/2 (= 1:2/3:16/27);
9/4:2:27/16 (= 1:8/9:3/4) ≠ 81/32:16/9:3/2 (= 1:512/729:16/27);
9/4:2:3/2 (= 1:8/9:2/3) ≠ 81/32:16/9:27/16 (= 1:512/729:2/3).In only the highlighted case 6:
a:c:e = b:d:f = 1:64/81:2/3
are the tone ratios of three mesēs in proportion to those of the three other modes. Starting with the Phrygian mode, the first three alternating modes:
Phrygian __ Hypolydian __ Hypodorian
have meses in exact proportion to those of the other three alternating modes:
Dorian __ Hypophrygian __ Mixolydian
Meses of the former are one interval higher than their counterparts (compare 81/32 with 9/4, 2 with 16/9 & 27/16 with 3/2). The six modes below the Lydian (L) can therefore be divided into two triads:
with the one-to-one correspondences:
Phrygian (P)
Dorian (Do* ),
Hypolydian (HL)Hypophrygian (HP)
and
Hypodorian (HD)
Mixolydian (M)
The mesēs of the first, third and fifth modes after the Lydian are in the same decreasing proportion 1:64/81:2/3 as those of the second, fourth and sixth modes, corresponding
___________________________
*The abbreviation ‘Do’ is used here instead of ‘D’ to avoid confusion in subsequent discussion with the musical note D.13
mesēs being separated by a whole interval and each triad of modes spanning the interval of a perfect fifth. In Section 2 it was likewise found that the first, third and fifth notes after the tonic of the Pythagorean scale uniquely have the same relative proportions of their tone ratios as the second, fourth and sixth notes after the tonic, whilst corresponding notes are an interval apart, each triad of notes spanning a fifth. Moreover, this increasing proportion is 9/8:4/3:27/16, that is, 2/3:64/81:1. So these two triads of notes increase in pitch in exactly the same proportions as the mesēs of the Mixolydian–Hypophrygian–Dorian and Hypodorian–Hypolydian–Phrygian triads. Clearly, the triadic structure of the Pythagorean scale is reflected in the musical modes themselves through their mesēs, with the following one-to-one correspondences:
The Lydian mode with one non-Pythagorean note corresponds to the tonic C and the perfectly Pythagorean Hypolydian mode corresponds to the perfect fifth G. Just as this note is the arithmetic mean of the tonic and the octave, so the mesē of the Hypolydian mode is the middle note of the two octaves of 15 notes, as well as the geometric mean of their lowest and highest notes because 2/1 = 4/2. So the seven Greek modes comprise the Lydian and two triads in harmonic proportions, just as the seven notes of the Pythagorean scale consist of the tonic and two triads of notes in similar proportions. These triads have 15 non-Pythagorean notes, their prescription by the Godname YAH with number value 15 indicating their significance in their own right, as the next section will explain.
6. Sephirothic basis of the musical modes
Mathematically speaking, there can be only seven distinct musical modes. Each mode is separated by one note and so any mode beyond the seventh would, as Ptolemy pointed out in the case of Aristoxenus’ eighth ‘Hypermixolidian’ mode, repeat the scale on the next lower or upper octave and would not differ fundamentally from its counterpart amongst the group of seven modes. But what is the metaphysical reason for this number? It was proposed in Section 2 that there exists a one-to-one correspondence between the seven notes of the Pythagorean scale and the seven Sephiroth of Construction because both display a 3:3:1 pattern in their respective descents. This would mean that the reason for the ancient Greeks always regarding musical scales as descending in pitch is that this matches the 3:3:1 pattern in the descending order of emanation of the Sephiroth of Construction. It does not imply, of course, that they were familiar with the mystical teachings of modern Kabbalah, which did not exist then. They had their own mystery religions, such as Orphism, in which, too, there was a septenary scale of being:
1. The Ineffable
2. Being
3. Life
4. Intellect
5. Soul
6. Nature
7. Body14
These levels were further divided into triads to create the Orphic theogonies (11). Instead, the Greeks originally saw music as the language of the soul, the various musical modes expressing different levels of the soul, and so scales had to be regarded as descending in order to reflect naturally the evolutionary descent of the soul into the material world. The correct way of ordering the notes of the scale was inverted for practical reasons when musical theorists such as Aristoxenus broke away from what he saw as the metaphysical theories underpinning music and
restructured scales according to their key. Although, therefore, this article will use the language of Kabbalah, the ideas that it expresses are universal, for the divine archetypes have filtered into the mystical consciousness of many ancient cultures, assuming many names but retaining the same ten-, seven- and three-fold structures as those that manifest in the Tree of Life.
Set out below are the correspondences between the seven notes of the Pythagorean scale, their corresponding scales and the seven Sephiroth of Construction:
In order to maintain the analogy between the two triads of Sephiroth of Construction and the two triads of notes separated by a tone interval, the natural order of the notes in the Pythagorean scale cannot follow the sequence of Sephiroth. Notice that the Phrygian mode and the Dorian mode assigned, respectively, to Geburah and Hod on the Pillar of Judgement are counterbalanced by their hypo versions assigned to, respectively, Chesed and Netzach on the Pillar of Mercy (Fig. 10). The Mixolydian mode has no hypo version that is different to itself. This is consistent with its assignment to a Sephirah on the central pillar. Just as the perfect fifth G is the mathematical centre of gravity of the Pythagorean scale, so the Mixolydian mode (G scale) is assigned to the Tiphareth at the centre of the Tree of Life. Just as Malkuth is the completion of the Tree of Life, so, too, the Hypolydian mode is the mathematically perfect realisation of the seven types of musical scales.
The spheres in Fig. 10 symbolising the seven Sephiroth of Construction are coloured with the seven colours making up white light, the order of emanation of the former following
15
the sequence of the latter, with the colour red assigned to Malkuth. This explains the particular assignment in Tables 1 & 2 of the rainbow colours to the seven musical modes.
The Hypolydian mode is the perfect mode vis-à-vis its position relative to the other six modes because, according to Fig. 5, its ‘mesē by position’ (fourth note up from the lowest note of the seven) coincides with its ‘mesē by function’ (the mesē of the two-octave system from which the mode was extracted). This note is G, the perfect fifth, whose special Pythagorean character is the fact that it is the fourth note in the descending sequence of the seven notes of the Pythagorean scale. Pythagoreans believed that all phenomena belonged to a four-fold hierarchy of complexity, the last completing its perfect wholeness. The fact that the fourth note of the fourth descending scale is also the fourth note of the descending Pythagorean scale therefore makes this mode ideal in this special Pythagorean sense, quite apart, of course, from its being the Pythagorean scale itself! The mesē of the Hypolydian mode is the first note of the Mixolydian mode and corresponds to Tiphareth at the centre of the Tree of Life. Its pivotal position is consistent with its assignment to Tiphareth, the geometrical and metaphysical centre of the Tree of Life. The Hebrew word ‘Tiphareth’ means ‘beauty,’ not in its common, aesthetic connotation but in the sense of the Greek word ‘harmonia’ used by the Pythagoreans to indicate the perfect balance of function and appearance. The Hypolydian mode is unique among the modes in exhibiting the full mathematical harmony of the Pythagorean scale.
The Dorian and Phrygian modes are assigned to the Pillar of Judgement, which expresses the receptive, nurturing, reproductive aspect of Creation, its ‘feminine’ aspect. Plato regarded the Dorian mode as masculine and the Lydian mode as feminine. It is important to understand that such gender-assigned qualities of music have nothing to do with the more fundamental polarities of the Pillars of Mercy and Judgement, which are entirely metaphysical, not psychological. The other modes were called by the names of various peoples whose kinds of music expressed some of their racial traits. The qualities of music played in a given scale have nothing to do with a particular note in the Pythagorean scale that acts as its tonic. They would possibly have more to do with the mesē of the mode in question, its frequent repetition setting the psychological tone of musical compositions played in this mode. We also need to keep in mind that the musical scales codified and simplified by Bishop Ambrose of Milan in the fourth century are not identical to those known by these labels to the ancient Greeks. This makes precise correlation between the known psychological qualities of their modes and the Sephiroth impossible, for the scales to which these modes originally referred are unknown, apart, perhaps, from the Dorian scale (D scale). Indeed, some musicologists reject (mistakenly) the belief that these ancient musical modes were based upon different scales!
It is probably simplistic to suppose that there is a precise correlation between the Sephiroth of Construction, whether in terms of their positive virtues or the negative human vices associated with them, and the psychological characteristics attributed by the ancient Greeks to their musical modes, even if they could be identified. Human nature is a complex mixture of all the qualities represented by these Sephiroth, even though some national characteristics of various peoples undoubtedly find expression in the art of their country, such as its music. Even supposing that such a correlation really exists, what were the emotional excesses of some modes may be due, not to the positive attributes of a Sephirah but to its negative aspects, for a lack of a positive Sephirothic quality or virtue in a human being manifests as its associated opposite quality, or vice.
7. Tree of Life nature of the seven musical scales
Evidence for the sacred nature of the seven Greek modes (sacred, that is, in this — and
16
only this — sense: they are the musical counterpart of the cosmic blueprint called the ‘Tree of Life’) is that the Hebrew divine names mathematically prescribe the composition of their notes. In particular, the Godname YAHWEH, conforms to its meaning as the creative essence of God by defining the total number of Pythagorean notes making up the seven scales other than their tonics. It in effect ‘creates’ the domain or matrix of musical notes that crystallises into the shape of seven distinct scales. Think of an amorphous cloud of 26 Pythagorean notes and 16 non-Pythagorean notes grouping into the 42 notes between the tonic and octave of the seven scales. The first is analogous to how the trunk of the Tree of Life (Fig. 11) is made up of 26 geometrical elements, namely, ten points, ten straight lines, five triangles and one tetrahedron, which form the ‘skeleton’ of the full Tree of Life. Including their seven octaves, the seven modes comprise (7×7=49) notes above the tonic made up of 26 Pythagorean notes and (16+7=23) other notes.
This corresponds to the 26 geometrical elements of the trunk of the Tree of Life and the 23 elements (12 lines and 11 triangles) outside its trunk.* This precise correspondence shows that the seven modes are the musical counterpart of the Tree of Life; the 26 Pythagorean notes make up their essential body and the 23 octaves and non-Pythagorean notes lie outside it, just as 23 geometrical elements exist outside the trunk of the Tree of Life. Actually, there is also a tetrahedron outside the trunk with its corners at Kether, Chokmah, Binah and Tiphareth (see Fig. 2), making a total of 50 geometrical elements prescribed by the Godname ELOHIM with number value 50 and creating a 26:24 distinction between the trunk and its exterior. Likewise, the 49 notes of the seven modes descend from the 50th note, G3, which is the second octave of the Mixolydian mode and the 15th note of the two octaves spanned by all the modes. So there is a similar 26:24 division between Pythagorean notes belonging to musical modes and octaves, non-Pythagorean notes and the parent note G3. The following correspondences are established:
Tetrahedron outside trunk G3 (source of 7 modes) 23 lines & triangles outside trunk 23 octaves & non-Pythagorean notes 26 corners, edges & triangles of trunk 26 Pythagorean notes This 26:24 division is also found in the inner form of the Tree of Life as the first (6+6)
_______________________
*The Tree of Life has two tetrahedra and 16 triangles with 22 sides and 10 corners.17
enfolded, regular polygons (Fig. 12), which were shown in Article 4 to constitute a ‘Tree of Life pattern’ prescribed by the Godnames of the ten Sephiroth. In particular, they have 50 corners prescribed by ELOHIM, one set of six polygons having 26 corners (indicated in Fig. 12 by red dots) and the other set having 24 corners (shown by black dots) outside their shared, so-called ‘root edge’.
The implication of these correspondences between the musical composition of the seven modes and the Tree of Life or any equivalent Tree of Life pattern is that the former is the musical counterpart of the latter. The musical modes are sacred because they constitute a mathematical whole structured according to the divine blueprint of the Tree of Life. This explains why the Godnames are found to define the composition of their notes; they are the mathematical archetypes that prescribe the nature of this blueprint.
8. Pitch differences between modes & equal-tempered scale
The Pythagorean scale is divided into seven intervals, five of which are whole tones differing in pitch by 9/8 and two of which are leimmas, differing in pitch by 256/243. In the modern equal-tempered scale the scale is divided into twelve semitones separated by equal intervals, so that two semitones are together equal to one tone. This means that the difference in pitch between successive, equally tempered semitones = 21/12 and that the difference in pitch of a tone interval = 21/12 ×21/12 = 21/6. The tone ratios of the notes in this scale corresponding to those in the Pythagorean scale are:
The difference in pitch between two notes separated by a semitone is defined as 100 cents. This means that an octave spans 1200 cents because it spans 12 semitones. Two notes with pitches f1 and f2 separated by n semitones will have pitches in the ratio f2/f1 = 2n/12, that is, they differ by 100n cents. Therefore, n = 12log2(f2/f1), that is, their pitch interval in cents = 1200log2(f2/f1). Noting that log2X×log102 = log10X (13), where X is any
Table 3. Pitch interval between modal notes and their equal-tempered counterparts
Mode Lydian 0 +4 +8 +112 +2 +6 +10 0 Phrygian 0 -110 -106 -2 +2 -108 -104 0 Dorian 0 +4 -106 -2 +2 +6 -104 0 Hypolydian 0 +4 +8 -2 +2 +6 +10 0 Hypophrygian 0 -110 -106 -2 -112 -108 -104 0 Hypodorian 0 +4 -106 -2 +2 -108 -104 0 Mixolydian 0 +4 +8 -2 +2 +6 -104 0 (All figures other than 0 are approximated to the nearest integer)
18
positive number, their pitch interval = (1200/log102)log10(f2/f1) ≈ 3986.3log10(f2/f1).
This formula may be used to calculate the pitch differences in cents between the notes of the seven modes and their corresponding notes in the equal-tempered scale. Table 3 above shows in cents the difference: modal note pitch – equal-tempered pitch.
As a comparison, the Pythagorean tone interval 9/8 is 204 cents, slightly larger than the equal-tempered interval of 200,
and the leimma is about 90 cents, lower than the semitone of 100 cents. 21 of the 42 notes between the tonic and the octave are higher in pitch than their counterparts in the equal-tempered scale and 21 are lower in pitch (Fig. 13). The number value 21 of the Godname EHYEH is the number of notes either of higher or lower pitch than their counterparts. The Hypolydian mode is closest in pitch to the equal-tempered scale, or rather it ought to be said that this artificial scale is nearest the perfect Pythagorean scale compared with the other modes. With variations of pitch between 2 and 10 cents, the two are virtually indistinguishable to most ears, at least for single notes — chords can be another matter. Over the frequency range most common in music (500 Hz to 4,000Hz), the ear can just detect an interval of less than one-thirtieth of a semitone, i.e., about three cents (12). But it is harder to detect differences of pitch in real life than in the laboratory, and sensitivity falls below 500 Hz, dropping to about 30 cents at a frequency of 62 Hz. On the other hand, differences of pitch are easier to detect in musical sounds than in pure tones. All the notes of the Hypolydian mode except the perfect fourth are slightly higher in pitch than the modern scale. But all 16 non-Pythagorean notes differ sufficiently to be differentiated. 15 of them are lower in pitch than their equal-tempered counterparts. This is the number value of the Godname YAH, which is a curious coincidence because the equal-tempered scale cannot be said to be of God’s making! The Lydian mode is the only one whose notes are all lower in the equal-tempered scale, the fourth being more than a semitone lower (112 compared with 100). The Hypophrygian is the only mode whose notes in the modern scale are all higher than their classical counterparts, five of the seven notes being more than a semitone higher. Melodies played according to modes other than the Hypolydian on instruments tuned to the modern scale will sound differently to their playing according to their pure pitches.
9. Mirror symmetry of musical modes
The ancient Greeks thought in terms of descending musical scales. From a mathematical perspective, the issue of whether the modes should be generated from ascending or descending notes does not arise. It is only we humans who, finding it easier to think in
19
terms of increasing, rather than decreasing, numbers, wonder whether the modern view of the musical scale as ascending might be incompatible with its mathematical structure. The reason for this is as follows: writing the Pythagorean whole tone interval 9/8 as T and the Pythagorean leimma 256/243 as L and taking in turn successive intervals (not notes) between the tonic and the octave of the Pythagorean scale (Hypolydian mode), the seven modes ascending in pitch from left to right are:
Notice that: 1. the order of tone intervals in the Phrygian mode is the mirror image or reverse of that of the Hypolydian, 2. the Lydian is the reverse of the Hypophrygian, 3. the Mixolydian is the reverse of the Hypodorian, and 4. the Dorian is unique among the seven modes in that the orderings of its ascending and descending tone intervals are the same — it is its own mirror image. What does this reflection symmetry between pairs of modes (or within itself, in the case of the Dorian) imply? As only the relative ordering of tone intervals and leimmas defines the differences between the seven modes, not the absolute values of the pitches of their notes, it means that, if we started at any note of any mode and selected successive sets of descending notes with tone intervals of either 1/T or 1/L, we would get precisely the same sets of combinations of descending tone intervals as that shown above for the ascending notes. It makes no difference whether we regard the scales as descending (as the ancient Greeks did) or whether we think in terms of ascending scales (as musicians do now). This is because the seven descending modes are, in terms of their tone interval composition, the very same as the seven ascending ones, the remarkable mirror symmetry displayed by their sets of tone intervals generating seven, and only seven, different ways of ordering them. Each mode turns into another one (its mirror reflection) whilst the Dorian turns into itself. The difference between the descending and ascending sequences of notes is one of reflection of the order of their intervals. The ascending Phrygian (LTTTLTT) is like the descending Hypolydian (LTTTLTT) and vice versa, the ascending Lydian (TTTLTTL) is like the descending Hypophrygian (TTTLTTL) and vice versa, and the ascending Mixolydian (TTLTTLT) is like the descending Hypodorian (TTLTTLT) and vice versa. Perhaps one could say that the members of each pair are polar opposites, moving in opposite directions of pitch but similar in the pattern of ordering of their two types of intervals.
The seven musical modes therefore consist of three such chiral pairs, one the mirror reflection of the other, and one (Dorian) that is invariant with respect to reversing the order of its tone intervals. This can be represented by a hexagon with mirror image pairs at diametrically opposite corners and the mirror-symmetric Phrygian mode at its centre:
As well as turning into one another by reversal of the order of their tone intervals, the
20
seven modes are generated by successive translations of a Pythagorean interval or leimma:
0.
1.
2.
3.
4.
5.
6.T L T T T L T
L T T T L T T
T T T L T T L
T T L T T L T
T L T T L T T
L T T L T T T
T T L T T T LDorian
Phrygian
Lydian
Mixolydian
Hypodorian
Hypophrygian
Hypolydian(Numbers 1–6 indicate the number of translations). It does not matter where in the infinite sequence of successive intervals of the ascending Pythagorean scale:
.... T L T T T L T T L T T T L T T L T T T….
a sequence of seven, successive intervals is chosen as the starting point (the Dorian mode was arbitrarily chosen above) and then shifted upwards in pitch by an interval, for this translation will always generate one of the patterns of intervals of the seven musical modes (see figure below)). As we saw earlier, the same property of invariance is displayed if, choosing any starting point in this infinite sequence, we select successive sets of seven intervals shifted down in pitch by one interval. This is because the endless sequence of intervals of the Pythagorean musical scale has the very important property of being its own mirror image, as may be confirmed by selecting any interval in the sequence and writing the successive intervals descending below it: the pattern of T’s and L’s thus generated is the same, wherever the starting point, as the pattern of ascending intervals. This makes whether musical scales should be regarded as descending (as the ancient Greeks did) rather than as ascending an irrelevant question as far as their mathematical analysis is concerned.
The infinite sequence of intervals is composed of repeated cycles of seven sets of seven intervals because when, for example (referring to the list above), the Hypolydian mode is translated by one interval, it becomes the Dorian, i.e., the seventh mode in the list turns into the first one; further successive translations merely repeat the cycle. This becomes obvious when the seven intervals of an octave of any mode are represented by arcs of a circle:
(The smaller arc denotes the leimma (L) and the larger one denotes the Pythagorean tone interval (T)). Wherever one starts — whether, indeed, the selection is made in a clockwise or anticlockwise sense — there are seven, and only seven, different patterns of L’s and T’s that can be chosen sequentially. These are the sets of intervals defining the seven musical modes.
A cycle of seven modal octaves comprises 14 of the 15 notes of two complete Pythagorean octaves and has 13 intervals (nine tone intervals T and four leimmas L) with
21
a difference of pitch of (243/64=(3/2)5×1/2), i.e. one octave below five perfect fifths. n successive cycles span 7(n+1) notes with (7n+6) intervals spanning a tone interval of 243/64×2n-1 = (3/2)5×2n-2 , i.e., (n–2) octaves above the fifth perfect fifth. Notice that seven cycles of seven modes have 55 intervals spanning five octaves above the fifth perfect fifth and a tone interval of 243, where
2 3
4 5 6
7 8 9 10and 243 (=35) is the 26th overtone. The number value 26 of YAHWEH is therefore the number of overtones generated by seven cycles of seven modes. The number value 15 of Yah is the number of overtones generated by five cycles.
These Godnames are associated with cycles of five and seven. This can be regarded as the modal counterpart of an octave of any mode comprising seven intervals of which five are Pythagorean intervals of 9/8. In fundamental terms, it corresponds to the seven Sephiroth of Construction, the lowest five of which span the Lower Face of the Tree of Life.
The cyclic nature of the interval structure of the seven modes is best illustrated by a circle with seven points denoting the modes equally spaced along its circumference:
The Hypolydian and Phrygian turn into each other by either one reflection (denoted by the double-headed, dotted line arrow) or two successive, interval translations (denoted by solid line arrows). The Hypophrygian and Lydian change into each other by either one reflection or four successive translations. The Hypodorian and Mixolydian turn into each other by either one reflection or six translations.
22
The T/L interval structure of the seven modes with the same tonic and octave can be mapped (Fig. 14) by representing their 44 notes as points on three great circles that are 60° apart and intersect at the South Pole (tonic) and North Pole (octave) of a sphere. The longer arcs denote Pythagorean tones (T) with an interval of 9/8 and shorter arcs signify leimmas (L) with an interval of 256/243. As the reflection of the Hypolydian mode, the Phrygian musical scale spans a semicircle (solid line) opposite that spanned by the former scale. Its second note is diametrically opposite the penultimate note of the Hypolydian scale, its third note is diametrically opposite the sixth note, and so on. Similarly, the notes and intervals of the mirror image Lydian and Hypophrygian modes are diametrically opposite one another on another great circle (dotted line), as are the notes of the mirror image Mixolydian and Hypodorian modes lying on the great circle made up of dashes and dots. The notes of the Dorian mode are situated at points that are mirror images of one another along the vertical axis of the sphere connecting its poles.
Each of four modes (Dorian, Phrygian, Hypodorian & Hypophrygian) has four intervals that are different compared with those of the Hypolydian; two modes (Lydian & Mixolydian) have two intervals out of place with respect to this mode. We found on page 8 that the Lydian and Mixolydian each has one non-Pythagorean note. These two modes therefore most resemble the Hypolydian. Accordingly, the psycho-spiritual quality of music based upon them may be expected to be closer to that of the Hypolydian than the other four modes insofar as it depends upon the pattern of intervals making up the scale used to play it.
10. Conclusion
The Greek musical modes are not sacred because they were the basis of the music of ancient Greece or for any other historical or cultural reason. There is in fact no evidence that seven octave species were recognised as such then, at least in the popular culture, certainly not in the sense of the Gregorian modes of medieval Church music devised in the eight century CE. Also, the principles on which the modes were constructed and the way Greek theorists analysed and named them changed over the classical period. The incomplete and uncertain view that modern scholarship has regarding ancient Greek awareness of the modes does not, however, undermine the conclusions of this article, which are based upon mathematical analysis, Pythagorean and Kabbalistic principles, that is, a priori considerations, not upon partial, empirical evidence. It proposes that the Greek modes are sacred in the same sense that the Tree of Life at the heart of Jewish mysticism is sacred. They express the seven-fold, objective nature of God made manifest in imperfect man. Today’s popular music, focussing almost exclusively on romantic love, makes it sometimes hard to remember that music is really the language of the soul, of which emotion — even that of the romantic kind — is but the lowest expression. Through their mystery religions, the ancient Greeks knew that there are seven levels of being and seven sacred planets to which the seven strings of the lyre corresponded. Apollo, the Sun God, had a Greek title ‘Ebdomaios,’ meaning seven-fold. The musical modes not only formally correlate with this seven-fold nature of a human being but also actually express it in terms of the qualities of their music. The Hypolydian mode (C scale) is the ideal one musically because it alone contains all the seven notes of the Pythagorean scale. Even if it is right that the counterparts of the ‘hypo’ modes were unknown to ancient Greeks but were only invented or inferred in medieval times by the theoretical need to complement the Dorian, Lydian and Phrygian modes, the fact remains that there can exist only seven such scales, for they are generated from the seven successive notes of the Pythagorean scale below the octave. In this context, therefore, the number seven is not a cultural artefact. Instead, its presence in music is a powerful example of the cyclic nature of this
23
number. The 3:3:1 division of the seven Sephiroth of Construction, which finds precise parallels in the Orphic mystery tradition, has its counterpart in both the seven-fold Pythagorean scale and Greek modes. The former consists of the tonic and two triads of notes of the Pythagorean scale with tone ratios in similar proportions and separated by one interval, whilst the latter comprises the Lydian mode and two triads of modes whose corresponding mesēs are in the same proportion and one interval apart. This is not a mathematical coincidence but, instead, indicates a universal principle at work structuring both consciousness and its language — music — according to the same pattern. This is why Plato’s numbers of the World Soul generate the tone ratios of the Pythagorean scale, for the World Soul is precisely the same as the Kabbalists’ Adam Kadmon, namely, Universal Man, designed in the Image of God.
Because the ancient Greek modes are the exact, musical counterpart of this cosmic paradigm, melodies played according to them have qualities that must resonate in the awareness of the hearer because, as the human version of Universal Man, the latter, too, has a seven-fold spectrum of consciousness. The highest function of music is not to entertain, although this has its place, but to bring the hearer into awareness of all these levels, instead of focussing it on just the emotional one, as modern popular music does. Because the modern, equal-tempered scale does not reproduce the exact tonal frequencies of the Pythagorean scale, the potential power of music used during the rites of ancient Mystery religions like Orphism to resonate with different levels of human consciousness and to transport the hearer to higher states of awareness is completely absent from contemporary and classical music, even when composed with the genius of a Mozart or Bach. If this happens at all, as it does sometimes, when such composers seem to capture celestial harmonies, it is only by accident. The modern musical scale is solely a human invention, conceived largely in order to solve the practical problem that (mainly) keyboard instruments had in playing in different keys the Pythagorean scale some of whose notes have complex, fractional tone ratios to which it was very difficult to tune them. Although it may have been discovered (at least in the West) by a human being, namely Pythagoras, the unique mathematical beauty of the Pythagorean scale, its generation by the integers 1, 2, 3 & 4 symbolised by the tetractys symbol of 10-fold Divine Unity, the mathematical prescription of the seven modes by the ancient, Hebrew Godnames, as well as the Tree of Life pattern of their notes, all constitute evidence that its status transcends the purely pragmatic nature of its modern successor.
A musician may argue that the pitch differences between the notes of the Dorian and equal-tempered scales are not noticeable to the human ear, at least when played in quick succession as a musical composition, so that there cannot be any significant difference in the psycho-spiritual quality of music employing these scales. This might seem incontestable as a scientific argument if, as it assumes, consciousness were merely the product of a brain whose neurological activity is affected by nerve signals issuing from the organ of Corti in the fluid-filled cochlea of the inner ear when set vibrating by sound waves in the air. However, many traditions of esoteric knowledge contradict the unproved, presupposition of modern science that the brain creates consciousness. Furthermore, they regard sounds as vibrations not only in air but also in a subtle medium that some Indian mystical traditions call ‘akasha.’ This allows the possibility (albeit not yet confirmed by orthodox science) that humans have non-physical organs of perception that create the counterparts of optical vision and hearing on a higher level of consciousness, the latter, for example, being the phenomenon known to parapsychology as ‘clairaudience.’ In fact, according to yoga, this organ is the ‘vishuddha chakra’ located in the region of the throat (14). Utilizing non-physical aspects of sounds that are unknown to science but familiar to yogis through their use of mantras, such an organ belonging to one
24
of the vehicles of higher consciousness described by these traditions might be responsive only to the precise, natural pitches of the Pythagorean scale, even though most ears cannot easily differentiate its notes from those of the modern equal-tempered scale. This is because, as Plato said, both the World Soul, of which the human soul is a reflection, and the Pythagorean musical scale share the same mathematical pattern, which means that the former must be tuned in a subtle way to the latter through a principle of correspondence. Higher states of awareness, evoked by a principle of sympathetic resonance with brain waves akin to that familiar to any acoustic scientist studying the effects of sound on matter, might in principle be induced in someone who was listening to music played on an instrument tuned exactly to the Pythagorean scale.
Table 4. Gematria number values of the Sephiroth in the four Worlds.
ANGELS
CHAKRA1 Kether
(Crown)
620EHYEH
(I am)
21Metatron
(Angel of the Presence)
314Chaioth ha Qadesh
(Holy Living Creatures)
833Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
6362 Chokmah
(Wisdom)
73YAHWEH, YAH
(The Lord)
26, 15Raziel
(Herald of the Deity)
248Auphanim
(Wheels)
187Masloth
(The Sphere of
the Zodiac)
1403 Binah
(Understanding)
67ELOHIM
(God in multiplicity)
50Tzaphkiel
(Contemplation of God)
311Aralim
(Thrones)
282Shabathai
Rest.
(Saturn)
317Daath
(Knowledge)
4744 Chesed
(Mercy)
72EL
(God)
31Tzadkiel
(Benevolence of God)
62Chasmalim
(Shining Ones)
428Tzadekh
Righteousness.
(Jupiter)
1945 Geburah
(Severity)
216ELOHA
(The Almighty)
36Samael
(Severity of God)
131Seraphim
(Fiery Serpents)
630Madim
Vehement Strength.
(Mars)
956 Tiphareth
(Beauty)
1081YAHWEH ELOHIM
(God the Creator)
76Michael
(Like unto God)
101Malachim
(Kings)
140Shemesh
The Solar Light.
(Sun)
6407 Netzach
(Victory)
148YAHWEH SABAOTH
(Lord of Hosts)
129Haniel
(Grace of God)
97Tarshishim or
Elohim
1260Nogah
Glittering Splendour.
(Venus)
648 Hod
(Glory)
15ELOHIM SABAOTH
(God of Hosts)
153Raphael
(Divine Physician)
311Beni Elohim
(Sons of God)
112Kokab
The Stellar Light.
(Mercury)
489 Yesod
(Foundation)
80SHADDAI EL CHAI
(Almighty Living God)
49, 363Gabriel
(Strong Man of God)
246Cherubim
(The Strong)
272Levanah
The Lunar Flame.
(Moon)
8710 Malkuth
(Kingdom)
496ADONAI MELEKH
(The Lord and King)
65, 155Sandalphon
(Manifest Messiah)
280Ashim
(Souls of Fire)
351Cholem Yesodoth
The Breaker of the
Foundations.
The Elements.
(Earth)
16825
Indeed, is this not unlike the very calming, uplifting effect that the Dorian mode played by a piper had on the angry youth in the legendary tale about Pythagoras told by Iamblichus? What modern tunes played even with the skill of the great flutist, James Galway, would have this effect on rowdy youth in a wine bar? Perhaps the mood-changing pitches of sounds played by a properly tuned instrument are just as powerful (if not more so) as the melody? Perhaps we should regard a human being as like a musical instrument tuned to the ‘music of the spheres.’ The purpose of life is to play this instrument so that all its potential melodies of consciousness become alive. Then at last, like Pythagoras, we shall hear the divine harmonies within us and the instrument shall become its player.
“In Egypt, when priests sing hymns to the gods,
they sing the seven vowels in due succession and
the sound of these vowels has such euphony that
men listen to it instead of the flute and the lyre."
Demetrius, c. 200 B.C.E.
(Quoted by Aristotle in his Poetics )Acknowledgements
I wish to thank Annabel Shaxson for introducing me to the musical modes of ancient Greece and for providing useful material on this topic to study. I am also very grateful for her encouragement and for her valuable discussions with me.
References
1) Life of Pythagoras, translated by Thomas Taylor, London, 1818, ch. 15.
2) Ibid., ch. 25.
3) The Pythagorean Plato, Ernest G. McClain (Nicolas-Hays, Inc., 1984).
4) Pol.1342a 32-b 12, cf. 1340b4, Procl. Chrestomathy, ap. Phot. Bibl. 320b.
5) Pol. 1342b12, cf. 1340b4.
6) The Hymns of Orpheus, Hymn XXXIII, translated by Thomas Taylor (The Philosophical Research Society, Inc., Los Angeles, California, 1981).
7) Music in Ancient Greece and Rome, John G. Landels (Routledge, 1999), p.101.
8) Ancient Greek Music, M.L. West (Clarendon Press, Oxford, 1994), pp. 228-229.
9) Numbers written in boldface are the number values of the ten Sephiroth of the Tree of Life in the four Worlds of Atziluth, Beriah, Yetzirah & Assiyah. They are shown in Table 4 above.
10) Phillips, Stephen M. Article 1: “The Pythagorean Nature of Superstring & Bosonic String Theories,” (WEB, PDF), p. 5.
11) Orpheus, G.R.S. Mead (John M. Watkins, 1965), p. 61.
12) Let log2X = Y and log10X = Z. Then X = 2Y = 10Z . Taking the logarithm to base 10 of each side of this equation, Ylog102 = Z, as log1010 = 1. Therefore, Y= Z/log102 = log10X/log102 = log2X. Therefore, log2X×log102 = log10X.
13) The Physics of Music, 7th ed., Alexander Wood (Chapman and Hall, 1975), p. 83.
14) Yoga, Ernest Wood (Penguin Books, 1965), p. 149.26