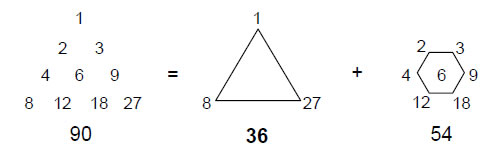by
Stephen M. Phillips

Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.

Website: http://www.smphillips.mysite.com

Abstract

1

1. Interval composition of the eight Church musical modes
Article 16¹ analysed the notes and intervals of the eight musical modes used in plainsong by the Roman Catholic Church for hundreds of years. They consist of four ‘authentic modes’: Dorian (D scale), Phrygian (E scale), Lydian (F scale) and Mixolydian (G scale), and four ‘plagal modes’: Hypodorian (A scale), Hypophrygian (B scale), Hypolydian (C scale) and Hypomixolydian (D scale):

Although the same D scale as the Dorian mode, the Hypomixolydian mode has a different dominant, or reciting note, and a different finalis, or ending note. The C scale (Hypolydian mode) is the Pythagorean musical scale. The tone ratios of its notes are:

1      9/8      81/64      4/3      3/2      27/16      243/128      2

Table 1 shows the tone ratios of the notes in the eight Church musical modes:

Table 1.

Musical scale	Tone ratio
D scale	1	9/8	32/27	4/3	3/2	27/16	16/9	2
C scale	1	9/8	81/64	4/3	3/2	27/16	243/128	2
B scale	1	256/243	32/27	4/3	1024/729	128/81	16/9	2
A scale	1	9/8	32/27	4/3	3/2	128/81	16/9	2
G scale	1	9/8	81/64	4/3	3/2	27/16	16/9	2
F scale	1	9/8	81/64	729/512	3/2	27/16	243/128	2
E scale	1	256/243	32/27	4/3	3/2	128/81	16/9	2
D scale	1	9/8	32/27	4/3	3/2	27/16	16/9	2

(White cells denote Pythagorean notes; red cells denote non-Pythagorean notes.)

The seven different types of musical scale have 42 notes between the tonic and octave. They comprise 26 Pythagorean notes and 16 non-Pythagorean notes, showing how the Godname YAHWEH² with number value 26 prescribes the Pythagorean character of the seven octave species. As 42 is the 21st even integer, EHYEH, the Godname of Kether, prescribes the seven types of scales. EL ChAI, the Godname of Yesod with number value 49, prescribes the seven scales because there are 49 intervals between their notes. The eight modes have 48 notes between the tonic and octave comprising 30 Pythagorean notes and 18 non-Pythagorean notes. Including tonics and octaves, the 64 notes are made up of (30+16=46) Pythagorean notes and 18 non-Pythagorean notes. 48 is the number value of Kokab, Mundane Chakra of Hod. 64 is the number value of Nogah, Mundane Chakra of Netzach, the Sephirah preceding Hod in the Tree of Life.

Table 2 lists the numbers of each kind of note/interval found in the eight Church modes (Pythagorean intervals are those whose magnitudes equal the tone ratios of notes in the Pythagorean musical scale).

2

Table 2. Numbers of notes/intervals in the eight Church musical modes.

Tone ratios written in red denote non-Pythagorean notes or intervals. Tone ratios of Pythagorean and non-Pythagorean notes are listed separately in order of increasing size. A musical scale has eight notes with 36 intervals (eight ‘1’s — the unit intervals between each note and itself — and 28 intervals between its notes). The eight modes have (8×36=288) intervals, where 288 = 1¹ + 2² + 3³ + 4⁴. This demonstrates how the Tetrad Principle³ determines the total number of intervals between the (8×8=64=4³) notes in the eight scales. They comprise 64 ‘1’s and (8×28=224) intervals between notes. Eight of them are octaves. (224–8=216) intervals are not octaves. 216 is the number value of Geburah. The number value 36 of ELOHA, Godname of this Sephirah, is the number of intervals between the eight notes of a musical mode, whilst its own number value is the number of intervals other than octaves in all eight modes The 216 intervals comprise 140 Pythagorean intervals, where 140 is the number value of Masloth, the Mundane Chakra of Chokmah, called ‘the Sphere of the Zodiac.’ They also include 76 non-Pythagorean intervals. YAHWEH ELOHIM, Godname of Tiphareth with number value 76, prescribes the non-Pythagorean tone intervals. Notice that there are 50 non-Pythagorean intervals of value 729/512 (×6), 256/243 (×16) and 32/27 (×28) and 26 non-Pythagorean intervals of size 128/81 (×10), 16/9 (×12) and 1024/729 (×4). This 50:26 division is reflected in the number values of ELOHIM (50) and YAHWEH (26).

Including the eight octaves, the eight modes have (140+8=148) Pythagorean intervals, where 148 is the number value of Netzach, the eighth Sephirah. Of the 288 intervals, eight are octaves, leaving 280 intervals below the octave, where 280 is the number value of Sandalphon, the Archangel of Malkuth. There are 64 ‘1’s, where 64 is the number value of Nogah, the Mundane Chakra of Netzach. There are (64+8=72) ‘1’s and ‘2’s, where 72 is the number value of Chesed, the fourth Sephirah. The number value 72 of the first Sephirah of Construction measures the number of intervals in the eight Church modes that are ‘1’s or ‘2’s, whilst the number value 216 of the second Sephirah of Construction measures the number of intervals that are not ‘1’s or ‘2’s!

The 14 types of notes in the eight Church modes are, in order of increasing tone ratios:

1   256/243   9/8   32/27   81/64 4/3   1024/729 | 729/512   3/2   128/81   27/16   16/9   243/128   2.

These notes make up the seven different musical scales and belong not just to the eight modes but to any set of eight scales in which one scale is repeated. They are the basic musical ‘atoms,’ so to speak, that make up the chain molecules called the Church musical modes. The 14 different notes of the seven musical scales consist of seven pairs of notes and their so-called ‘complements,’ the note whose tone ratio is the

3

interval between its partner and the octave:

	Note	Complement
1.	1	2	1×2 = 2
2.	256/243	243/128	256/243×243/128 = 2
3.	9/8	16/9	9/8×16/9= 2
4.	32/27	27/16	32/27×27/16 = 2
5.	81/64	128/81	81/64×128/81 = 2
6.	4/3	3/2	4/3×3/2 = 2
7.	1024/729	729/512	1024/729×729/512 = 2

The vertical line drawn in the row of 14 tone ratios separates the first seven notes from their complements. Between the tonic and octave are six Pythagorean notes and six non-Pythagorean notes, i.e., the 14 notes comprises eight Pythagorean notes and six non-Pythagorean notes. As noted earlier, the 216 intervals between notes that are not ‘1’s or ‘2’s comprise 140 Pythagorean intervals and 76 non-Pythagorean intervals. There are (216–12=204) repetitions of these basic note intervals comprising (140–6=134) Pythagorean intervals and (76–6=70) non-Pythagorean intervals.

The 48 notes between the tonic and octave of the eight musical modes can be represented by points on a sphere (Fig. 1). Its North Pole denotes the octave, the South Pole denotes the tonic and the 36 intermediate notes of the six scales other than the two D scales are spread along three Great Circles spaced 120° apart, the 12 notes of the two D scales being distributed along their shared, vertical diameter. The Godname ELOHIM with number value 50 prescribes the 50 notes on the sphere and the Godname ELOHA with number value 36 prescribes the 36

notes that surround its axis, which is made up of 14 notes. The numbers of notes with a given tone ratio are shown below:

The tone ratio 729/512 appears only once as a note, according to Table 1, but six times

4

as an interval, according to Table 2, i.e., five times as an interval between notes above the tonic. Similarly, the tone ratio 1024/729 appears only once as a note but four times as an interval, i.e., three times as an interval between notes above the tonic.

The spherical distribution of 50 notes representing the eight Church musical modes constitutes a holist system with a Tree of Life pattern shown by the 50 corners of the two sets of the first six enfolded polygons making up the inner form of the Tree of Life (Fig. 2). The ends of the ‘root edge’ shared by each set of polygons symbolize the tonic at the South Pole and the octave at the North Pole. The 24 corners outside the root edge of one set denote the 24 notes. Their mirror image counterparts in the other set denote the 24 complements of these notes. The

six external corners of an octagon denote the six notes above the tonic up to the perfect fourths of the Dorian and Hypomixolydian modes arranged along the vertical axis of the sphere. Their six counterparts in the other octagon denote the six complementary notes. As shown in Article 40,⁴ this 24:24 division is a characteristic feature of holistic systems.

Table 3 gives the numbers of intervals, notes and intervals other than notes, i.e., intervals between notes above the tonic.

Table 3. Interval composition of the eight Church musical modes.

5

Each different tone ratio appears more than once. There are 168 intervals other than notes. This is remarkable because 168 is the number value of Cholem Yesodoth, the Mundane Chakra of Malkuth, which has been shown in previous articles to appear in many different contexts because it characterises all holistic systems (for example, it is the structural parameter of superstrings). This is excellent evidence of the holistic nature of the eight Church musical modes. More remarkable still, Table 3 shows that the number value 78 of Cholem (Fig. 3) is the number of intervals other than notes that are major seconds, thirds or perfect fourths and that the number

value 90 of Yesodoth is the number of the nine remaining types of intervals.

We found earlier than there are 204 repetitions of the basic set of 12 intervals between the tonic and octave of the eight Church musical modes. As they have 216 intervals between their tonics and octaves and as 12 notes of the two D scales lie on the axis of the three Great Circles along which their notes are arranged, there are also 204 intervals other than notes of the Dorian mode and its plagal counterpart, the Hypomixolydian mode with the same set of notes:

1      9/8      32/27      4/3      3/2      27/16      16/9      2

Instead of arranging their notes along the axis, the 12 basic notes between the tonic and octave may be arranged along it, the 48 notes (30 Pythagorean, 18 non-Pythagorean) between the tonic and octave of the eight modes being assigned to points along four Great Circles. One half-circle represents an authentic mode and the other half-circle represents its plagal counterpart. Including the tonic and octave, there are now not 38 notes but 50 notes (32 Pythagorean, 18 non-Pythagorean) lying on

6

Great Circles. Including the 12 basic types of notes (6 Pythagorean, 6 non-Pythagorean) between the tonic and octave that make up the eight musical modes, we now have 62 notes arranged on the sphere and its axis. They comprise (32+6=38) Pythagorean notes and (18+6=24) non-Pythagorean notes. (38–2=36) Pythagorean notes and 24 non-Pythagorean notes are distributed around the tonic and octave at its poles. (36–6=30) Pythagorean notes and (24–6=18) non-Pythagorean notes surround its axis, on which are the tonic, the octave, six Pythagorean notes and six non-Pythagorean notes.

Compare this pattern of 62 notes with the 62 vertices of the disdyakis triacontahedron (Fig. 4). The Catalan solid with the most edges, it was proved in previous articles to be the polyhedral version of the inner form of the Tree of Life. It has the 12 (B) vertices of an icosahedron, the 20 (C) vertices of a dodecahedron and 30 (A) vertices that are apices of pyramids attached to the 30 Golden Rhombic faces of the rhombic triacontahedron whose 32 vertices belong to these Platonic solids. With a straight line passing through two diametrically opposite C vertices, this vertical axis is surrounded by 30 A vertices, (20–2=18) C vertices and 12 B vertices. The following correspondence exists between the 60 vertices between the apex and nadir and the 60 notes either on Great Circles or on the central axis between the tonic and the octave at the Poles:

30 A vertices         30 Pythagorean notes;
12 B vertices         12 basic notes between tonic and octave;
(2+18) C vertices 2 Pythagorean notes (tonic/octave) + 18 non-Pythagorean notes.

The two opposite C vertices denote the tonic and octave, the remaining 18 C vertices denote the 18 non-Pythagorean notes, the 30 A vertices denote the 30 Pythagorean notes and the 12 B vertices denote the 12 basic notes between the tonic and octave of the eight musical modes. This correlation between the sacred geometry of the disdyakis triacontahedron and the spherical representation of the Church modes demonstrates the holistic nature of each system. It also gives a defining role to the icosahedron.

The spherical distribution with notes of the two D scales arranged along the axis comprise the tonic, octave, eight Pythagorean notes and four non-Pythagorean notes on the axis and 24 Pythagorean notes and 12 non-Pythagorean notes surrounding it. This does not correlate with the disdyakis triacontahedron in a natural way because both Pythagorean and non-Pythagorean notes have to be assigned to vertices of a given type, apart from the fact that there are no notes for the 12 B vertices. Even if the 12 basic types of notes between the tonic and octave were assigned to the 12 B vertices and the 50 notes to the 30 A and 20 C vertices, their 32 Pythagorean notes other than the tonic and octave and their 16 non-Pythagorean notes cannot be assigned to either the 28 A & 20 C vertices (axis passing through two opposite A vertices) or the 30A and 18 C vertices (axis through two C opposite vertices) without both types of notes being assigned to each type of vertex. In the case where the central axis was made up of the 12 basic notes, their six Pythagorean notes and six non-Pythagorean notes were assigned to the 12 B vertices. So there is mixing here as well, but only for B vertices, whereas, when the notes of the two D scales lie on the axis, each type of note has to be assigned to both A and C vertices.

An alternative way of correlating notes with vertices is to consider the axis of the polyhedron passing through two A vertices. There are 12 vertices in the equator, 24 vertices between it and the apex and 24 vertices between it and the lowest vertex. This (24+12=36):24 pattern correlates with the 36 Pythagorean notes and 24 non-Pythagorean notes in the basic set of 12 notes and in the 48 notes of the eight modes.

Table 4 shows the number of repetitions of intervals in the eight Church modes.

7

The 204 repetitions of the basic set of 12 notes between the tonic and octave comprise 136 intervals (91 Pythagorean, 45 non-Pythagorean) and 68 complements (43 Pythagorean, 25 non-Pythagorean). There are 134 repeated, Pythagorean intervals and 70 repeated non-Pythagorean intervals. There are 36 repeated notes/complements (24 Pythagorean, 12 non-Pythagorean) and (204–36=168) repeated intervals that are not notes/complements (78 Pythagorean intervals with tone ratios up to that of the perfect fourth, 90 Pythagorean & non-Pythagorean intervals other than these).

Just as there are 168 intervals between notes above the tonic in the eight Church modes (78 intervals that are seconds, thirds and perfect fourths, 90 other intervals), so there are 168 intervals other than notes that are repetitions of the 12 types of notes between the tonic and octave (78 Pythagorean intervals that are seconds, thirds and perfect fourths, 90 others). Once again, two sets of intervals define the number values of the Hebrew words ‘Cholem’ and ‘Yesodoth’ in the name of the Mundane Chakra of Malkuth. This cannot be coincidental because the two numbers refer to similar sets of notes. The 168 intervals consist of 110 Pythagorean and 58 non-Pythagorean ones.

The Tetrad Principle defines the 136 repeated intervals up to 1024/729 because

136 =	1	2	3	4
	5	6	7	8
	9	10	11	12
	13	14	15	16

It defines the 78 Pythagorean intervals up to the perfect fourth because

78 =	1	2	3	4
	12			5
	11			6
	10	9	8	7

It defines the 168 intervals other than notes that are repetitions of the basic set of 12 notes between the tonic and octave because

168 =	3	5	7	9
	25			11
	23			13
	21	19	17	15

8

The Tetrad Principle defines the 45 repeated, non-Pythagorean intervals in this set because 45 is the fourth hexagonal number after 1.⁵ It defines the 70 repeated, non- Pythagorean intervals in the set of 204 repetitions of the basic set of 12 notes because 70 is the fourth member after 1 of the class of four-dimensional, tetrahedral numbers.⁶ It defines the 36 repeated notes and their complements because 36 is the sum of the first four even integers and the first four odd integers. It defines the 64 notes of the eight modes because 64 = 4³. It defines the 16 tonics and octaves because 16 = 4². It defines the 48 notes between the tonic and octave because 48 = 4³ – 4². The Tetrad Principle always defines global properties of holistic systems, e.g., the four authentic and the four plagal Church modes, and the four notes in a mode and their four complements.

Table 5 displays the number of pairs of repeated intervals and their complements and the numbers of intervals and their complements that are unpaired.

Table 5. Numbers of paired and unpaired repeated intervals.

Interval	Number of paired intervals	Number of unpaired intervals
1	0	0
256/243	3	12
9/8	11	28
32/27	13	14
81/64	9	10
4/3	27	6
1024/729	3	0
729/512	3	2
3/2	27	0
128/81	9	0
27/16	13	0
16/9	11	0
243/128	3	0
2	0	0

The 204 repeated intervals include 66 pairs of intervals and their complements (90 Pythagorean, 42 non-Pythagorean). ADONAI, the Godname of Malkuth, prescribes the number of repeated pairs because 66 is the 65th integer after 1. There are 72 unpaired intervals (44 Pythagorean, 28 non-Pythagorean). This is the number value of Chesed, the fourth Sephirah. Altogether, there are 216 intervals other than octaves. This is the number value of Geburah, the Sephirah following Chesed. Its Godname ELOHA with number value 36 prescribes the 36 notes between the tonic and octave of the six modes arranged on the three Great Circles on the sphere. The 204 repeated intervals comprise 134 Pythagorean intervals and 70 non-Pythagorean intervals. As 134 is the 67th even integer, it shows how the number value 67 of Binah determines the number of repeated, Pythagorean intervals. The Godname EHYEH of Kether with number value 21 prescribes the 42 non-Pythagorean intervals in the 66 pairs of repeated intervals because 42 is the 21st even integer.

Let us return to the spherical distribution of the 50 notes, with the tonic and octave assigned to the South and North poles, the 12 notes (8 Pythagorean, 4 non-Pythagorean) of the two D scales between them arranged along the axis and the 36 notes of the six other modes between the tonic and octave arranged along the six semicircles of the three vertical Great Circles inclined at 120° to one another. The 204 repetitions of the 12 basic types of intervals between notes of the eight Church modes comprise 134 Pythagorean intervals and 70 non-Pythagorean intervals. (134–8=126)

9

Pythagorean intervals are therefore not notes of the D scales. Including the tonic and octave, there are 10 Pythagorean notes arranged along the central axis, 70 non- Pythagorean intervals and 126 Pythagorean intervals, that is, 206 intervals, where

206 = 126 + 10 + 70,

126 = 37(9/8) + 19(81/64) + 31(4/3) + 25(3/2) + 11(27/16) + 3(243/128),

10 = 1(1) + 2(9/8) + 2(4/3) + 2(3/2) + 2(27/16) + 1(2),

and

70 = 5(729/512) + 15(256/243) + 27(32/27) + 9(128/81) + 11(16/9) + 3(1024/729).

The 206 intervals comprise the tonic, octave, and 204 repetitions of the 12 basic types of notes making up the eight Church modes. They consist of 136 Pythagorean intervals and 70 non-Pythagorean intervals.

2. The Tree of Life nature of the eight Church musical modes
Consider a set of overlapping Trees of Life. The lowest tree (the ‘1-tree’) consists of 19 triangles with 11 vertices. Its ‘trunk’ consists of the geometrical sequence of a point, line, triangle and tetrahedron defined, respectively, by Kether, the path connecting Chokmah and Binah, the triangle whose vertices are the location of Chesed, Geburah and Tiphareth and the tetrahedron formed by Netzach, Hod, Yesod and Malkuth. The remainder of the 1-tree constitutes its ‘branches.’ Now suppose that the triangles are each divided into their three sectors and that each

sector is then turned into a tetractys (Fig. 5). The 1-tree is composed of (19×3=57) tetractyses with 251 yods. Its trunk is composed of five triangles that transform into 15 tetractyses. This shows how YAH, the

10

Godname of Chokmah with number value 15, prescribes the trunk of the 1-tree. The trunk comprises 80 yods. There are (57–15=42) tetractyses in the branches of the 1-tree with (251–80=171) yods. Creating 14 triangles, they comprise 42 centres of tetractyses. As there are six hexagonal yods inside each triangle on the edges of tetractyses, there are (14×6=84) such yods in the branches. There are (42+84=126) hexagonal yods inside the triangles making up the branches of the 1-tree.

It was explained in Article 32⁷ that the 80 yods of the trunk of the 1-tree symbolize the 80 bones of the human axial skeleton and that the 126 hexagonal yods in its branches created by the transformation of each triangle into three tetractyses symbolize the 126 bones of the appendicular skeleton (Fig. 6). It was also shown that the 206 bones of the human skeleton are encoded in the inner form of three overlapping Trees of Life representing the three spatial dimensions of the physical body of Adam Kadmon — the human prototype. As Fig. 5 shows, the three sets of enfolded polygons have 206 corners, the hexagons and dodecagons having 80 corners that symbolize the 80 bones of the axial skeleton and the remaining polygons having 126 corners that symbolize the 126 bones of the appendicular skeleton. The 42 centres (blue yods) of the tetractyses in the branches correspond to the 42 corners of the six octagons. The 84 hexagonal (red) yods on edges of tetractyses in the branches correspond to the 84 corners of the six triangles, the six squares, the six pentagons and the six decagons.

In the case of the 1-tree, the 206 yods comprise Kether, Malkuth, 78 yods in its trunk and 126 yods in its branches. In the case of the polygons enfolded in three trees, the 206 corners consist of the two topmost corners of the pair of hexagons enfolded in the third tree, 78 corners of hexagons and dodecagons and 126 corners of the remaining polygons. As we shall shortly see, this 2:78:126 division has a musical meaning in the context of the spherical representation of the notes of the Church musical modes. As stated earlier, the composition of the 126 repeated, Pythagorean intervals is:

126 = 37(9/8) + 19(81/64) + 31(4/3) + 25(3/2) + 11(27/16) + 3(243/128).

In the 1-tree and in the inner form of three overlapping trees, the number 126 splits into 42 and 84 (see Fig. 5). There is only one combination of sets with 42 intervals — the 31 perfect fourths and the 11 sixths. The composition of the 10 Pythagorean notes in the two D scales arranged on the axis is:

10 = 1(1) + 2(9/8) + 2(4/3) + 2(3/2) + 2(27/16) + 1(2).

They correspond to the 10 yods located at the positions of the 10 Sephiroth of the 1-tree and to the 10 external corners of the three hexagons belonging to the set of 21 polygons enfolded on one side of the three overlapping trees. The composition of the 70 non-Pythagorean intervals is:

11

70 = 5(729/512) + 15(256/243) + 27(32/27) + 9(128/81) + 11(16/9) + 3(1024/729).

They correspond to the 70 yods in the 1-tree that are not located at Sephiroth and to the 70 corners of the six dodecagons and the three hexagons in the set of 21 polygons enfolded on the other side.

As the starting point of a musical scale, the tonic should be assigned to Kether, the starting point of the 1-tree. As the completion of a scale, the octave should be assigned to Malkuth, its lowest point. The eight remaining Pythagorean notes of two D scales are assigned to the eight Sephiroth between these extremities and to the lowest and highest corners of the three hexagons that are joined by their corners. Adding them to the 70 non-Pythagorean intervals, the 206 intervals consist of the tonic, the octave, 78 intervals (8 Pythagorean, 70 non-Pythagorean) and 126 Pythagorean intervals — the same pattern as that found in the 1-tree and in the inner form of three overlapping trees.

This demonstrates the Tree of Life nature of the interval composition of the eight Church musical modes. The 10 Pythagorean notes on the axis of their spherical representation act as the ten Sephiroth, the South and North poles corresponding to Kether and Malkuth. The representation has notes increasing in pitch as their location move northwards towards the octave at the North Pole. This choice was made in order to reflect the natural association of height with pitch. However, this convention is arbitrary and the tonic could be assigned, instead, to the North Pole in order to maintain spatial correspondence with the 1-tree.

3. The eight Church musical modes as polyhedral geometry
The semi-regular polyhedra consist of the 13 Archimedean solids and their duals, the 13 Catalan solids. The simplest Catalan solid is the triakis tetrahedron (Fig. 7), a polyhedron with eight vertices, 18 edges and 12 faces formed by attaching tetrahedra to the four faces of a tetrahedron. Each edge is the side of an internal triangle with the centre of the polyhedron at its corner. It was shown in Article 29⁸ that the triakis tetrahedron is composed of 137 vertices, edges & triangles. In other words, it embodies the number that is central to modern physics in that its reciprocal is the so-called “fine-structure constant,” which measures the strength of the coupling of electric charges to the electromagnetic field. An axis passing through the centre and joining two opposite vertices consists of five geometrical elements (three vertices and two edges of internal triangles). (137–5=132) geometrical elements surround the axis and 136 elements surround its centre. This is the geometrical counterpart of the 136 repeated intervals in the eight Church modes up to the note with tone ratio 1024/729, their highest note

12

below the six complementary notes below the octave. The distinction between the tonic and these 136 repeated intervals corresponds to the geometrical distinction between the centre of the triakis tetrahedron and the 136 geometrical elements surrounding it. The six vertices surrounding its axis symbolize the six notes above the tonic up to that with tone ratio 1024/729. Alternatively, the eight vertices of the polyhedron correspond to the eight Pythagorean notes in the Dorian and Hypomixolydian modes lying on the axis of the spherical distribution of the 50 notes, whilst the other 126 geometrical elements surrounding the axis correspond to the 126 repetitions of the Pythagorean intervals in the eight modes. The triakis tetrahedron is therefore the polyhedral counterpart of the spherical arrangement of repeated Pythagorean notes and intervals. It is prescribed by ADONAI, the Godname  of Malkuth, because the minimum number

of geometrical elements needed to create it is 65,⁹ which is the number value of ADONAI.

We found in Article 27¹⁰ that, when the sectors of the faces and internal triangles of the triakis tetrahedron are each divided into three sectors and the latter then converted into tetractyses, it has 361 yods in 90 tetractyses. This is the number of acupoints in the 14 meridians of the human body, as established in Chinese acupuncture (Fig. 8). The 54 internal tetractyses and the 36 tetractyses in its faces conform to the 36:54 division in the Lambda tetractys,¹¹ whose 10 numbers determine the properties of holistic systems:

According to Table 1 of Article 27,¹² the triakis tetrahedron has 168 geometrical elements surrounding its axis when its internal triangles are each divided into three sectors. They correspond to the 168 intervals other than notes in the eight Church modes, i.e., the 168 intervals between their 56 notes above the tonic (78 seconds, thirds and perfect fourths, 90 other intervals — see Table 3). They also correspond to the 168 repetitions of the basic set of 12 notes between the tonic and the octave (78 seconds, thirds & perfect fourths, 90 other intervals — see Table 4)). Once again, this shows that

13

the geometrical composition of the triakis tetrahedron mirrors the composition of the intervals between musical notes. The 168 elements consist of 24 corners, 78 edges and 66 triangles. The number value 78 of Cholem is the number of edges and the number value 90 of Yesodoth is the number of vertices and triangles. The same 78:90 division appears in the triakis tetrahedron and in the two compositions of intervals! This is not coincidental, because both this polyhedron and the set of eight Church musical modes are manifestations of the universal
 

paradigm governing holistic systems. As such, they must embody the gematria number value 168 of the Mundane Chakra of Malkuth.

4. The last four enfolded polygons map the human skeleton
We saw in Section 3 that the inner form of three overlapping Trees of Life consists of 42 polygons with 206 corners. These 206 geometrical degrees of freedom symbolize the 206 bones in the human body whose three dimensions are represented by these three trees. This information is embodied also in the last four of the seven polygons making up the inner form of a single Tree of Life (Fig. 9). These polygons have 36 sectors prescribed by ELOHA, the Godname of Geburah with number value 36. They have

14

15

136 vertices, edges and triangles outside the root edge shared with the other set of polygons. This is the number of repeated intervals in the eight Church modes up to 1024/729. 206 yods are associated with the last set of four regular polygons. That this is not due to coincidence is demonstrated by the fact that 34 yods can be associated with the hexagon that symbolize the 34 single bones of the axial skeleton, 46 yods associated with the octagon symbolize the 46 bones of the axial skeleton forming pairs and 126 yods in the decagon and dodecagon symbolize the 126 bones of the appendicular skeleton. That such a detailed correlation could arise by chance is highly implausible. Moreover, the 80 yods associated with these four polygons that symbolize the 80 bones of the axial skeleton consist of two yods on the root edge and 78 yods outside it. This 2:78:126 pattern was found in Section 2 in the 206 yods of the 1-tree, which comprise Kether, Malkuth, 78 yods of the trunk and 126 yods in its branches, as well in the three sets of polygons enfolded in three trees, whose 206 corners consist of the two topmost corners of the pair of hexagons enfolded in the third tree, 78 corners of hexagons and dodecagons and 126 corners of the remaining polygons. It demonstrates that the 2:78:126 division is intrinsic to a holistic system. It manifests in the human skeleton as the distinction between the axial skeleton, which protects the vital organs, and the appendicular skeleton, which provides mobility and dexterity.

The same pattern was found in Article 41 in the set of seven pyramids whose bases are the seven regular polygons. The seven polygons divided into their 48 sectors are the projections of these pyramids. When their internal triangles and faces are divided into three sectors, the 432 sectors of the seven pyramids have 206 vertices¹³ (Fig. 10). They comprise 80 vertices in the pyramids whose bases are the first four polygons and 126 vertices in the last three pyramids. Their musical counterpart is the spherical distribution of 50 notes belonging to the eight Church modes, with the 12 basic notes between the tonic and octave arranged along its axis as the generative musical elements. The seven pairs of basic notes and their complements correspond to the seven pairs of apices of pyramids and centres of their bases.

5. The disdyakis triacontahedron embodies numbers 137, 206 & 168
There are 15 sheets of vertices perpendicular to an axis joining two diametrically opposite C vertices of the disdyakis triacontahedron. The central layer is a hexagon with six A vertices. On either side, sandwiched between the two opposite C vertices, are 6-sided polygons with six A vertices and six C vertices, and five triangles with three A, three B, three C, three A & three B vertices. When the sectors of the polygons are turned into tetractyses, the eight sheets in one-half of the polyhedron contain 206 yods (Fig. 11).¹⁴ They are made up of 34 corners and centres of the uppermost seven polygons, 46 yods that are either centres of these polygons or on the edges of the central hexagon and 126 other yods. They symbolize, respectively, the 34 single bones of the axial skeleton, the 46 bones in it that are grouped in pairs and the 126 bones of the appendicular skeleton. The bone composition of the human body is defined by the eight different sheets of polygons in the disdyakis triacontahedron.
When the 60 sectors of the 15 polygons are each divided into three triangles, the 180 triangles have 135 vertices,¹⁵ that is, 134 vertices surround the centre of the polyhedron. They correspond to the 134 repeated Pythagorean intervals in the eight Church modes. Including the two C vertices not belonging to polygons, the disdyakis triacontahedron is made up of 137 vertices. This is how it embodies the number 137 defining the fine-structure constant. It is the counterpart of the 137 geometrical elements composing the triakis tetrahedron (see Section 3).

According to Fig. 9, 206 yods are associated with the last four enfolded polygons. The

16

17

dodecagon has 69 yods outside the root edge. Associated with the hexagon, octagon and decagon are (206-69=137) yods. Both the number of bones and the fine-structure constant number 137 are embodied in the last four polygons!

Figure 12 shows the spectacular way in which the most important number in physics is embodied in the inner form of the Tree of Life. When the 94 sectors of the two sets of enfolded polygons are each divided into three triangles and the latter then turned into tetractyses, the resulting 282 tetractyses contain 1370 yods, i.e., the yods in 137 tetractyses! 282 is the number value of Aralim, the Order of Angels assigned to Binah.

The last four polygons also embody the number at the heart of superstring theory, which predicts that 496 particles transmit the forces between superstrings. There are 496 yods in the last four enfolded polygons other than their corners and centres (Fig. 13).¹⁶ Lest this should be thought a coincidence, it must be pointed out that the first and fourth of these have 248 yods and the second and third polygons have 248 yods. 248 is the dimension of the superstring gauge symmetry group E₈ and 496 is the dimension of E₈×E₈', the gauge symmetry group associated with the E₈×E₈' heterotic superstring. It is highly implausible that it could be mere chance that both the superstring numbers 248 and 496 should be the exact yod populations of certain combinations of polygons.

18

Of the 180 edges of the disdyakis triacontahedron, 12 edges (four A-B, four B-C & four A-C) are in the equatorial plane perpendicular to an axis joining two diametrically opposite A vertices (Fig. 14). There are 84 edges (28 A-B, 28 B-C & 28 A-C) above these and 84 similar edges below them. The number 168 is the number of edges that generate the 3-dimensional form of the disdyakis triacontahedron. That this number defines its shape can also be seen from the following consideration: the polyhedron has 60 vertices, 180 edges and 120 triangular faces (360 geometrical elements) surrounding any axis passing through two opposite vertices. When these vertices are A vertices, there are seven sheets of vertices perpendicular to the axis.

The fourth sheet of vertices in the equatorial plane of the polyhedron defines a 12-sided polygon with 12 vertices and 12 edges, totalling 24 geometrical elements. (360–24=336) elements lie above and below the equator, 168 on each side. 168 edges therefore shape the polyhedron above and below its equator, each part being composed of 168 geometrical elements. 
 

As discussed in Article 40,¹⁷ this beautiful property of the disdyakis triacontahedron is the geometrical manifestation of the 168 automorphisms of PSL(2,7), the symmetry group of the Klein quartic equation. This group is isomorphic to the symmetry group SL(3,2) of the Fano plane representing the algebra of the octonions.¹⁸

The 180 edges of the disdyakis triacontahedron are sides of internal triangles that meet at its centre. Suppose that each of the 180 internal triangles is divided into their three sectors. This creates (3×180=540) triangles. Including its 120 triangular faces, the polyhedron is composed of (120+540=660) triangles. There are 62 vertices in its faces, one vertex at its centre and 180 vertices of the 540 triangles in its interior, totalling 243 vertices. The line joining each polyhedral vertex to the centre is an edge of a triangle.

19

There are three edges of sectors inside each original, interior triangle. The number of edges = 180 + 62 + 3×180 = 782. The number of vertices, edges and triangles = 243 + 782 + 660 = 1685. The central axis is composed of three vertices and two edges of triangles, i.e., five geometrical elements. Therefore, 1680 geometrical elements surround the axis of the disdyakis triacontahedron. Apart from the Pythagorean factor of 10 (a tetractys is composed of 10 yods), the number value 168 of the Mundane Chakra of Malkuth determines the geometrical composition of the disdyakis triacontahedron! As discussed in many previous articles,¹⁹ the number 1680 is the number of circularly polarized oscillations made in each of the 10 closed curves of the heterotic superstring as it winds five times around its axis of spin, each revolution comprising 336 oscillations and each half-revolution comprising 168 oscillations. As the microscopic manifestation in space-time of the Tree of Life, the Mundane Chakra of Malkuth is the superstring constituent of the protons and neutrons inside atomic nuclei. Its gematria number value 168 is the number of circular oscillations made during a half-revolution of each closed curve, the superstring being created by 16800 such oscillations.

6. The last four enfolded polygons embody the number 168
The last four enfolded regular polygons have 168 yods outside their shared edge on the boundaries of their 36 tetractyses (Fig. 15). This demonstrates par excellence the shape-defining character of this number, discussed in many previous articles as a structural parameter of the heterotic superstring. Moreover, the 168 yods divide into the 84 yods on edges of the 18 sectors of the octagon and decagon and the 84 yods on the edges of the 18 sectors of the hexagon and dodecagon — the same two pairs of polygons that define the split of the superstring parameter 496 into 248 and 248. We encountered a similar division earlier for the disdyakis triacontahedron, which has 84 edges above its equator and 84 edges below it when its axis passes through two diametrically opposite A vertices. The 336 yods outside the root edge on the boundaries of both sets of the last four polygons correspond to the 336 geometrical elements in the faces of the disdyakis triacontahedron that are above and below its equator.

The seven pyramids whose bases are the seven regular polygons constituting the inner form of the Tree of Life have 336 vertices, edges & triangles surrounding their axes.²⁰ The so-called ‘n-pyramid’ (a pyramid with an n-sided regular polygon as its base) has 7n geometrical elements surrounding the axis joining its apex and base centre. The 3-pyramid, 4-pyramid, 5-pyramid & 12-pyramid have 168 elements surrounding their axes, as do the 6-pyramid, 8-pyramid & 10-pyramid.

The Tetrad Principle defines the numbers 84 and 336 because

84 = 1² + 3² + 5² + 7²

and

336 = 2² + 6² + 10² + 14².

The eight Church musical modes have 216 intervals below the octave, of which 48 intervals are notes, leaving 168 intervals that are not notes. There are (216–48=168) rising intervals and 168 falling intervals, the latter having tone ratios that are reciprocals of those of the former. This is the musical counterpart of:
1. the (168+168) yods on the edges of the two sets of the last four enfolded polygons;
2. the (168+168) geometrical elements above and below the equator of the disdyakis triacontahedron;
3. the (168+168) geometrical elements surrounding the axes of the seven pyramids whose bases are the seven regular polygons of the inner Tree of Life.

20

All are examples of holistic systems that are characterized by the same set of parameters, such as 168, 137 and 206.

References

¹ Phillips, Stephen M. Article 16: “The tone intervals of the seven octave species and their correspondence with octonion algebra and superstrings,” (WEB, PDF).
² The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation). They have number values obtained by the practice of gematria, wherein each letter of the Hebrew alphabet has a number assigned to it, giving a number value to a word that is the sum of the values of its letters. The Hebrew names, their translations and their number values are shown in the table below:

Table 1. Number values of the ten Sephiroth in the four Worlds.

	SEPHIRAH	GODNAME	ARCHANGEL	ORDER OF ANGELS	MUNDANE CHAKRA
1	Kether (Crown)                  620	EHYEH (I am)                  21	Metatron (Angel of the Presence)                  314	Chaioth ha Qadesh (Holy Living Creatures)                  833	Rashith ha Gilgalim First Swirlings. (Primum Mobile)                  636
2	Chokmah (Wisdom)                  73	YAHWEH, YAH (The Lord)                  26, 15	Raziel (Herald of the Deity)                  248	Auphanim (Wheels)                  187	Masloth (The Sphere of the Zodiac)                  140
3	Binah (Understanding)                  67	ELOHIM (God in multiplicity)                  50	Tzaphkiel (Contemplation of God)                  311	Aralim (Thrones)                  282	Shabathai Rest. (Saturn)                  317
	Daath (Knowledge)                  474
4	Chesed (Mercy)                  72	EL (God)                  31	Tzadkiel (Benevolence of God)                  62	Chasmalim (Shining Ones)                  428	Tzadekh Righteousness. (Jupiter)                  194
5	Geburah (Severity)                  216	ELOHA (The Almighty)                  36	Samael (Severity of God)                  131	Seraphim (Fiery Serpents)                  630	Madim Vehement Strength. (Mars)                  95
6	Tiphareth (Beauty)                  1081	YAHWEH ELOHIM (God the Creator)                  76	Michael (Like unto God)                  101	Malachim (Kings)                  140	Shemesh The Solar Light. (Sun)                  640
7	Netzach (Victory)                  148	YAHWEH SABAOTH (Lord of Hosts)                  129	Haniel (Grace of God)                  97	Tarshishim or Elohim                  1260	Nogah Glittering Splendour. (Venus)                  64
8	Hod (Glory)                  15	ELOHIM SABAOTH (God of Hosts)                  153	Raphael (Divine Physician)                  311	Beni Elohim (Sons of God)                  112	Kokab The Stellar Light. (Mercury)                  48
9	Yesod (Foundation)                  80	SHADDAI EL CHAI (Almighty Living God)                  49, 363	Gabriel (Strong Man of God)                  246	Cherubim (The Strong)                  272	Levanah The Lunar Flame. (Moon)                  87
10	Malkuth (Kingdom)                  496	ADONAI MELEKH (The Lord and King)                  65, 155	Sandalphon (Manifest Messiah)                  280	Ashim (Souls of Fire)                  351	Cholem Yesodoth The Breaker of the Foundations. The Elements. (Earth)                  168

(Numbers from this table appearing in the article will be written in boldface)

21

³ Phillips, Stephen M. Article 1: “The Pythagorean nature of superstring and bosonic string theories,” (WEB, PDF), p. 5.
⁴ Phillips, Stephen M. Article 40: “The unification of all sacred geometries and its implications for particle physics,” (WEB, PDF), pp. 23-28.
⁵ Wells, David. “The Penguin dictionary of curious and Interesting numbers,” Penguin Books, 1988.
⁶ Ibid, p. 60.
⁷ Phillips, Stephen M. Article 32: “Derivation of the bone & classical acupoint compositions of the human body and their relationship to the seven musical scales,” (WEB, PDF), pp. 9, 10.
⁸ Phillips, Stephen M. Article 29: “The triakis tetrahedron and the disdyakis triacontahedron embody the fine-structure constant and the structural parameter of the heterotic superstring,” (WEB, PDF), pp. 4-5.
⁹ Ibid, Table 3, p. 9, p.10.
¹⁰ Ref. 7, p. 22.
¹¹ Phillips, Stephen M. Article 11: “Plato’s Lambda — its meaning, generalisation and connection to the Tree of Life,” (WEB, PDF).
¹² Phillips, Stephen M. Article 27: “How the disdyakis triacontahedron embodies the structural parameter 1680 of the E₈×E₈ heterotic superstring,” (WEB, PDF), p. 4, Table 1.
¹³ Phillips, Stephen M. Article 41: “The pyramidal form of the inner Tree of Life, its counterparts and its encoding of the human skeleton,” (WEB, PDF), p. 6.
¹⁴ Phillips, Stephen M. Article 36: “The Sri Yantra-like pattern of the 15 layers of vertices in the disdyakis triacontahedron and its scientific meaning,” (WEB, PDF), p. 9, Table 4.
¹⁵ Ibid, p. 11.
¹⁶ Phillips, Stephen M. Article 34: “The seven layers of vertices in the disdyakis triacontahedron encode the 206 bones of the human skeleton, the superstring symmetry groups E₈ & E₈×E₈ and the superstring structural parameters 168, 336, 840 & 1680,” (WEB, PDF), p. 39.
¹⁷ Ref. 4.
¹⁸ Phillips, Stephen M. Article 15: “The mathematical connection between superstrings and their micro-psi description: a pointer towards M-theory,” (WEB, PDF), p. 12.
¹⁹ For example, see ref. 12.
²⁰ Ref. 13, p. 5

22