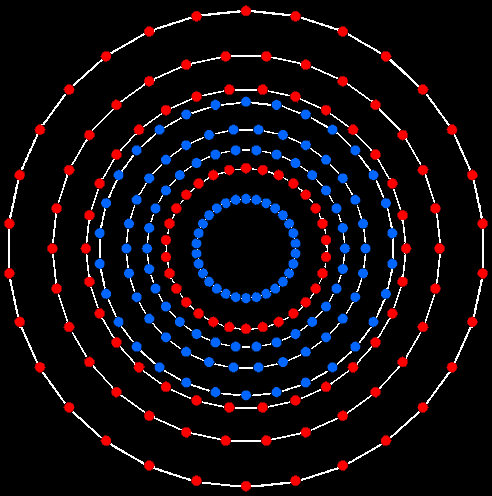
The
(4+4=8) triacontagons in the E8 Coxeter
plane of the 421 polytope.
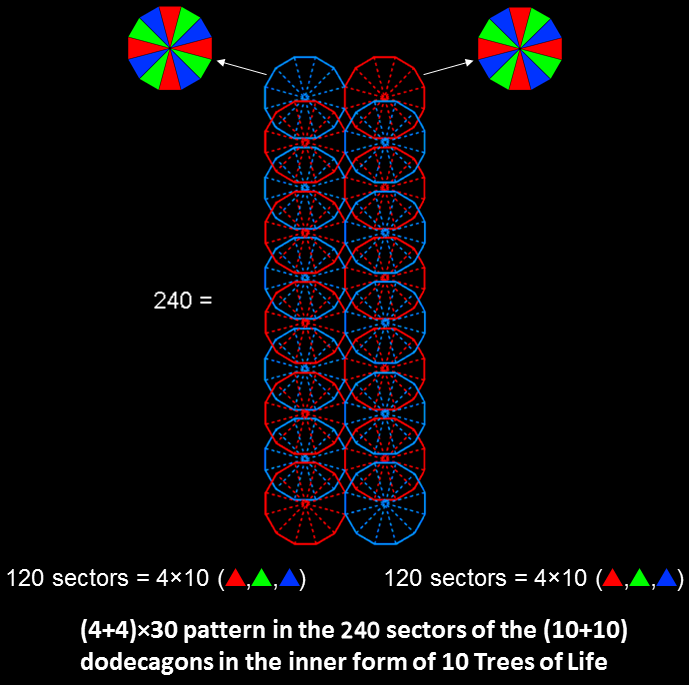
.png)
Surrounding the centre of the Type B dodecagon are 120 geometrical elements consisting of 5 types of lines (repeated 12 times), two points (×12) & 3 triangles (×12), i.e., 5 geometrical elements (×12). Therefore, 5 sets of 12 pairs of geometrical elements surround the centre. Each pair comprises a side of a triangle and either a corner or triangle. Every pair has its mirror image on the opposite side of the dodecagon. The 120 geometrical elements consist of 30 pairs and their 30 mirror images, i.e. 4 sets of 30 geometrical elements. The (7+7) polygons of the inner Tree of Life contain a pair of dodecagons. Surrounding the centres of the latter are (120+120=240) geometrical elements. They consist of (4+4=8) sets of 30 geometrical elements. These 240 geometrical elements are the counterparts of the 240 vertices of the (4+4=8) triacontagons in the E8 Coxeter plane projection of the 421 polytope. The factorisation 12 = 4×3 of the 12 sectors of the dodecagon, each with 10 geometrical elements, corresponds to the 4 triacontagons, each with 10 sets of 3 vertices. The pair of separate Type B dodecagons corresponds to the two sets of 4 triacontagons, each representing the projected vertices of a 600-cell.

The 5 Platonic solids constructed from tetractyses.

240 vertices & edges as 10 sets surround
a B-B axis of the disdyakis
triacontahedron.