| << Previous 1... 15 16 [17] 18 19 ...24 Next >> |
#17 The outer & inner Trees of Life with Type B polygons embody the E8×E8' heterotic superstring structural parameters 1680 and 2016 (Part 1)
As we have just seen, the outer & inner forms of the Tree of Life contain 1584 yods that are the counterpart of the 1584 yods up to the level of the apex of the 31-tree prescribed by EL. The 31-tree contains 1580 yods because the number of yods in the n-tree ≡ y(n) = 50n + 30, so that y(31) = 1580. The four yods outside it are the counterpart of the four yods in the root edge separating the two sets of seven enfolded polygons. The 1580 yods making up the body of the 31-tree correspond to the 1580 yods in the outer & inner Trees of Life outside its root edge. When its triangles are Type A, the number of yods in the n-tree ≡ Y(n) = 158n + 93 (see the diagram below for the derivation of this formula):

The number of yods in n overlapping Trees of Life with Type A triangles can be shown in similar fashion to be 158n + 56. Whether we are considering sections of n Trees or the n-tree, the number of yods in every 10 Trees of Life = 158×10 = 1580. Every new Tree adds 158 yods above the kite-shape whose corners are located at Tiphareth, Netzach, Hod & Malkuth. The significance of this number is not, simply, that it is the number of yods in 158 tetractyses but that it is the number of yods generated by successive emanation of 10 Trees of Life. This explains why it is embodied in the body of the 31-tree prescribed by EL ("God").
2016 yods in the outer & inner Trees of Life with Type B polygons
The number of yods in n overlapping Trees with (12n+4) Type A triangles = 158n + 56. The Type B triangle has 46
yods, which is 27 more than the Type A triangle. The number of yods in n Trees with Type B triangles ≡
YB(n) = 158n + 56 + 27(12n+4) = 482n + 164. Therefore, YB(1) = 646. Of these, 10 yods are
Sephirothic corners of triangles, leaving 636 yods, where 636 is the
gematria number value of Rashith ha Gilgalim ("First Swirlings"), the
Mundane Chakra of Kether. This number is also the sum of the numbers of the Godnames assigned to the 10 Sephiroth,
so that 646 = 10 + 636:

The archetypal nature of the number
636 is confirmed by the fact that it is is the number of hexagonal yods in the 2-d Sri Yantra
with 42 Type A triangles surrounding its central triangle, which is treated as a tetractys with six hexagonal yods
lining its sides:
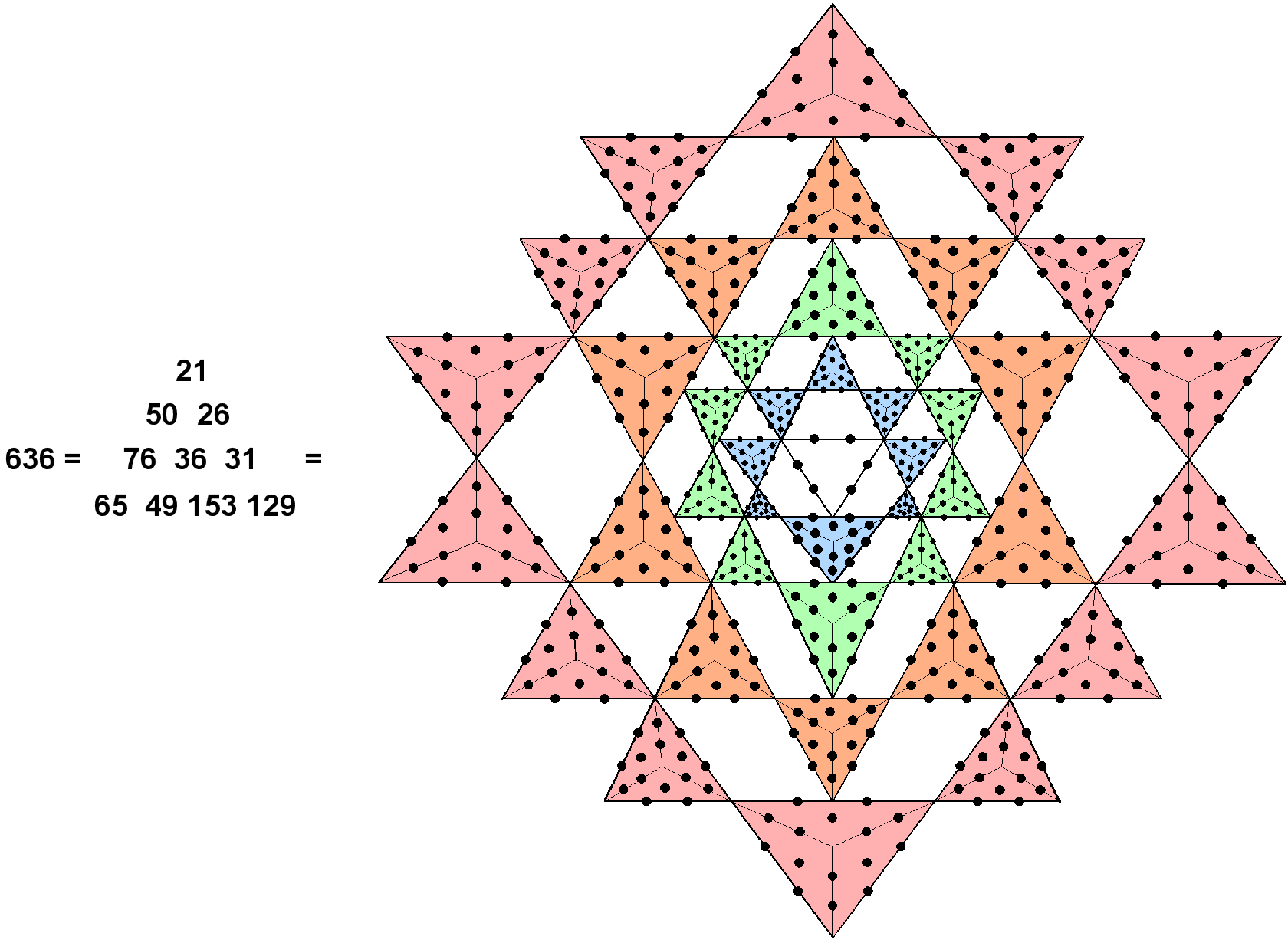
The number of hexagonal yods in the 42 triangles is the same, whether the 3-d or 2-d form of the Sri Yantra is considered. For the sake of consistency, the hexagonal yod at the centre of the central tetractys should be included, as its counterparts in the surrounding triangles are counted. However, this applies only to the 3-d version, as the bindu symbolising the Absolute coincides with its position and this is always excluded from the counting of yods or geometrical elements whose numbers have significance to the manifested cosmos (for the sake of clarity, the bindu dot is omitted from the 2-d version shown above). For the 2-d version, the number 636 refers to the number of hexagonal yods surrounding the bindu. For the 3-d version, it refers to the number of hexagonal yods surrounding the axis that passes through the centre of the central triangle and is perpendicular to the four layers of triangles. When the central triangle is regarded as Type A, having 19 yods, 10 yods other than its corners are added to these six hexagonal yods, so that there are (636+10=646) yods other than corners of the 43 triangles. They include the central yod of the central triangle, which can be counted in the case of the 3-d Sri Yantra because it lies directly below the bindu. The number 646 is the number of yods in the outer Tree of Life constructed from 16 Type B triangles. The Sri Yantra and the outer Tree of Life embody the same number!
The outer Tree of Life with Type B triangles has 646 yods, and the inner Tree of Life with Type B triangles has 1370 yods. Therefore, the separate outer & inner Trees of Life have 2016 yods:
646 + 1370 = 2016.
This number is the number of circular turns predicted to be in each helical whorl of the shadow matter superstring. As it was derived in earlier pages in a different context, this property must count as highly convincing evidence in support of the prediction, for it is very improbable that it could arise by chance. Indeed, so important is this property that it will be discussed in detaill in #21. When the outer & inner Trees of Life have polygons that are Type A, they contain
214 + 524 = 738
yods. Of these, seven yods in each set of seven polygons are their centres, leaving (738−4−7−7=720=10×72) yods outside the root edge that are not centres. This is how the number value 72 of Chesed determines this yod population. Each half of the inner Tree of Life with Type A polygons has 260 yods outside the root edge, so that the outer Tree and either half of the inner Tree have (214+260=474) yods. This is the number value of Daath ("knowledge").
A Type B triangle has four internal corners of 12 basic triangles. The 16 Type B triangles making up the outer Tree of Life have 10 corners symbolising the Sephiroth and (16×4=64) internal corners, i.e., 74 corners in total, where 64 is the number value of Nogah, the Mundane Chakra of Netzach. The (7+7) enfolded Type B polygons comprise 94 sectors with 80 corners, each sector being a Type A triangle having one internal corner of a basic triangle. The inner Tree of Life therefore has (94×3=282) triangles with (80+94=174) corners, where 282 is the number value of Aralim ("Thrones"), the Order of Angels assigned to Binah. The number of corners in the separate outer & inner Trees of Life with Type B polygons = 74 + 174 = 248. This is the number value of Raziel, the Archangel of Chokmah. It is also the dimension of the exceptional Lie group E8 — or, rather, E8′, as the context refers to the shadow matter sector whose symmetries belong to E8′. Here is confirmation that the yod population 2016 refers to the circularly polarised oscillations of each whorl of the E8-singlet state of the E8×E8′ heterotic superstring. The eight simple roots of E8′ are denoted by the six corners located at the positions of Sephiroth on the two side pillars of the outer Tree and the two corners located at Daath and Tiphareth (their projections onto the plane of the polygons are the two endpoints of the root edge); the remaining 240 corners denote its 240 non-zero roots:
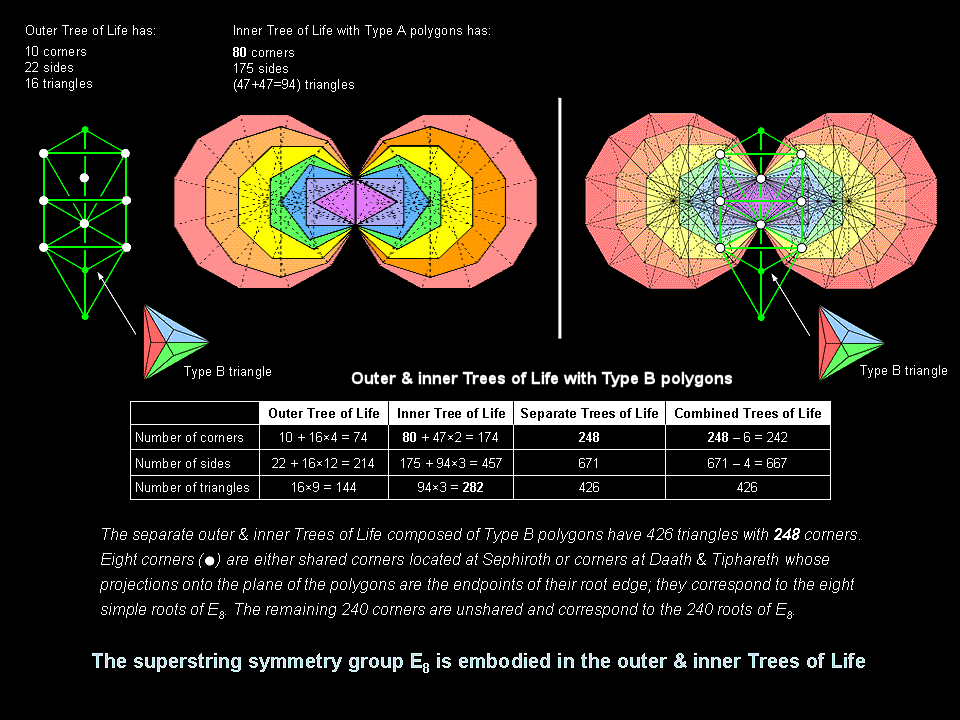
When the outer and inner Trees of Life with Type B polygons are combined, the six corners on the side pillars coincide with corners of sectors, so that there are now 242 corners. Two denote the two simple roots of E8′ that do not belong to E6′ and the other 240 corners consist of 72 corners belonging to the outer Tree, (80−6=74) corners of polygonal sectors that are intrinsic to the polygons and 94 corners inside sectors. There are (74+94=168) corners that are intrinsic to the inner Tree of Life. Therefore,
240 = 72 + 168.
Compare this with the fact that the 240 roots of E8′ consist of the 72 roots of its exceptional subgroup E6′ and 168 other roots. This division is characteristic of sacred geometries parameterised by these numbers and has been discussed in many examples (for example, see #23 in Wonders of Superstrings). But there are two sets of 74 corners: the 74 corners of the 144 triangles in the outer Tree of Life and the 74 corners of polygonal sectors that are unshared with triangles in the outer Tree. The question arises: which set should be combined with the set of 94 corners inside sectors? In other words, are the two simple roots of E8′ that do not belong to E6′ symbolised by the two endpoints of the root edge or by the corners located at Daath and Tiphareth in the outer Tree of Life whose projections onto the plane containing the polygons coincide with these endpoints? Analyses of the many examples of the embodiment by sacred geometries of the number 168 have indicated that they always display the division:
168 = 84 + 84.
However, this property cannot be used to resolve the ambiguity because the axial symmetry of the outer Tree and the fact that its triangles have an even number of corners makes it possible to define a left and a right half of it, each associated with 37 corners that can be combined with a respective left or right half of the inner Tree containing 47 corners inside sectors, thereby generating two sets of (37+47=84) corners, whilst, if the 74 corners refer to the polygons, 37 corners can be associated with each set of seven polygons with 47 internal corners, thereby creating two sets of 84 corners. Given the metaphysical distinction between the outer and inner Trees of Life, it seems more likely that the 168 roots of E8′ that are not roots of E6′ should be denoted by the 168 corners of triangles that all belong to the same (inner) form of the Tree of Life, rather than to both Trees.
The number of yods in the inner Tree of Life = 1370 = 12 + 372. The 12th prime number 37 is the number of corners in each suitably defined half of the outer Tree of Life with Type B triangles. It is also the number of yods inside a Type B triangle, as well as the total number of yods in a Type A hexagon. Each half of the 144 Polyhedron (one of the two polyhedra that constitute the Polyhedral Tree of Life) has 37 vertices because this polyhedron is the polyhedral counterpart of the outer Tree of Life, its 74 vertices comprising the 26 vertices of the disdyakis dodecahedron (the counterpart of the 26 corners of the 48 triangles making up the 16 Type A triangles) and 48 vertices of tetrahedra attached to the 48 faces of the disdyakis dodecahedron (see here).
The number of yods in the inner Tree of Life other than the six Sephirothic corners that are shared with the outer Tree of Life and symbolise six of the eight simple roots of E8′ = 1370 − 6 = 1364 = 41 + 42 + 43 + 44 + 45.
The first two terms (41 & 42) denote the 20 yods that are either the 12 unshared centres of polygons or the eight hexagonal yods lining the two side pillars that are shared with the inner Tree of Life. This leaves (43+44+45=1344) yods that are intrinsic to the inner Tree of Life and which surround the centres of the 14 polygons; they include (43=64) intrinsic corners, where 64 is the gematria number value of Nogah ("Glittering Splendour"), the Mundane Chakra of Netzach.
The number of corners of the 426 triangles in the combined Trees of Life = 242. Associated with each half of them are 121 corners, where
121 = 30 + 31 + 32 + 33 + 34.
As 63 = 20 + 21 + 22 + 23 + 24 + 25, the number of turns in each whorl of the shadow matter superstring is
2016 = 32×63 = 25(20+21+22+23+24+25) = 25 + 26 + 27 + 28 + 29 + 210.
As 25 = 32, this equation can be interpreted in the following way: starting with the number 32 as the 32 "Mystical paths of wisdom" expressed in the opening lines of the Jewish mystical book known as the Sepher Yetzirah ("Book of Creation") the first six terms in the geometric series up to 1024 (= 322):
32, 64, 128, 256, 512, 1024, 2048 ....
sum to 2016. This number is also the sum of the first 63 integers, i.e., it is the 63rd triangular number:
1 + 2 + 3 +... + 63 = 2016.
Using the data tabulated in the diagram shown above, the numbers of sides and the numbers of corners & triangles outside the root edge in each half of the combined Trees are shown below:
|
Left half |
Root edge |
Right half |
|
| Number of corners & triangles | 333 | 2 | 333 |
| Number of sides | 333 | 1 | 333 |
| Total | 666 | 3 | 666 |
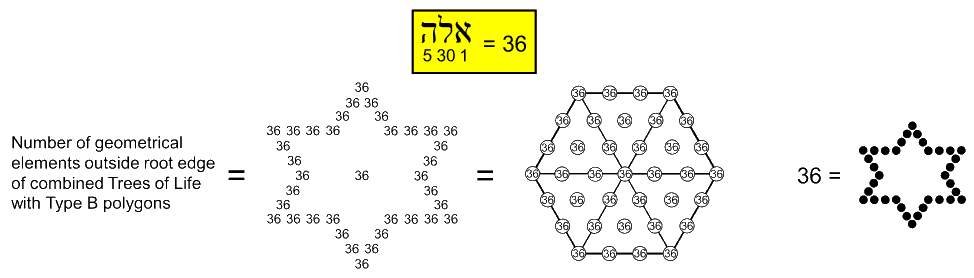
Here is remarkable evidence of beautiful design. As 333 = 9×37, the number of geometrical elements outside the root edge = 4×333 = 36×37 = 1332. This number can be represented by either a hexagram lined by 36 yods surrounding the central yod or a Type A hexagon with 37 yods, each yod weighted with the number value 36 of ELOHA (אלה), the Godname assigned to Geburah, which is the sixth Sephirah of Construction, counting from Malkuth:
This harmonises with the fact that 1332 = 36×37 = 36(1+36) = 62(60+62) = 62 + 64 and that there are 666 geometrical elements outside the root edge that are associated with each half of the combined Trees of Life. Denoted by black dots in the diagram below are the corners of triangles in the outer Tree of Life that coincide with Daath and Tiphareth and which define its root. Its trunk — the sequence of what is known in mathematics as the first four simplexes:
point-line-triangle-tetrahedron
— contains nine red corners that coincide with Sephiroth, five green centres of Type A triangles and 15 blue corners of their internal triangles. The 11 Type A triangles forming the branches of the outer Tree of Life have (11−1=10) green corners at their centres ("1" refers to Daath, which has already been counted as part of the root) and (11×3=33) blue corners of their internal triangles. There are 174 corners in the inner Tree of Life, of which 6 (denoted by white dots) are shared with the outer Tree and 168
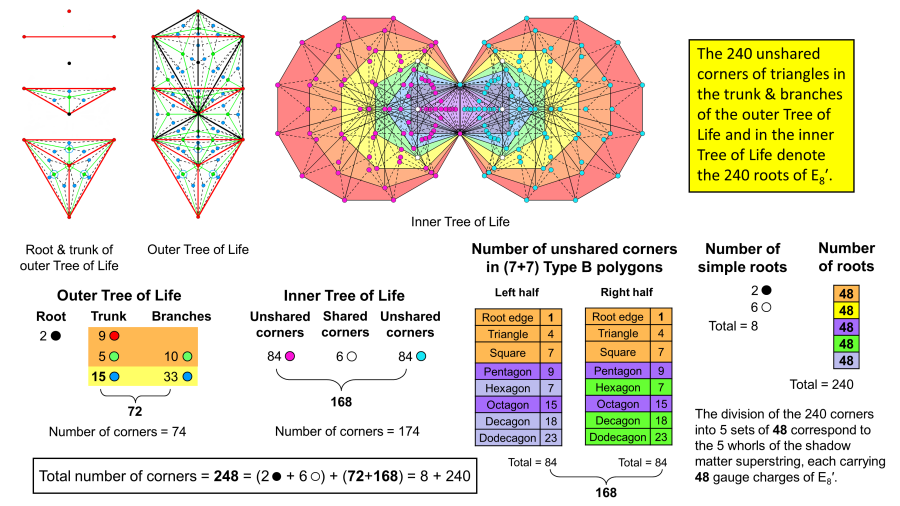
are unshared; 84 pink corners are associated with the left-hand set of 7 enfolded polygons and 84 turquoise corners are associated with the right-hand set of 7 polygons. If we tabulate their numbers of corners, the pair of triangles & squares highlighted in orange has 24 corners, the pair of pentagons & octagons highlighted in purple has 48 corners, the hexagon, decagon & dodecagon in one half highlighted in grey have 48 corners and their counterparts in the other half highlighted in green have 48 corners. Combining the 24 corners in the trunk & branches with the 24 corners in the triangles & squares generates a fourth set of 48 corners, and combining the blue corners in the outer Tree creates a fifth set of 48 corners. The 240 corners in the combined outer & inner Trees of Life form five natural groups of 48 corners. This is the geometrical basis of the five whorls of the shadow matter superstring, each of which carries 48 gauge charges of E8' when this symmetry is unbroken. Each whorl corresponds to a set of 48 corners.
It may be asked why this correlation between corners of triangles and the 240 roots of E8′ should not also apply to E8. But, of course, it does! However, when the triangles are Type B, their yod population is equal to the predicted number of turns in the five helical whorls of the shadow matter superstring. This property indicates that the symmetry group being represented in this context should be E8′, not E8, for the turns are the circularly polarised oscillations generated by pairs of plane waves representing its gauge charges. The fact demonstrated above that the 240 corners symbolising its roots form five sets of 48 corners in a non-random way is consistent with earlier analysis that predicts that — given that one revolution of a whorl always comprises 336 turns — a whorl belonging to the shadow matter superstring has to make six revolutions around the spin axis of the particle in order to have 2016 turns: 6×336 = 2016. This number, of course, refers to its ground state in the generation of states with the lowest masses. The excited whorls in heavier states will have more turns, perhaps corresponding to yods in the outer & inner Trees of Life composed of triangles that are Type C, Type D, etc. As we do not know yet whether some kind of Standard Model pattern applies to shadow matter, we cannot be certain whether its basic particles display several generations.
The five-fold division of the 240 corners of the Type B polygons in the separate outer & inner Trees of Life has an arithmetic counterpart as well. As 48 = 72 − 1 = 3 + 5 + 7 + 9 + 11 + 13,
240 = 5×48 = 5(3+5+7+9+11+13).
This number is the sum of (5×6=30) red and blue odd integers that can be arranged to form the five points of a pentagram:
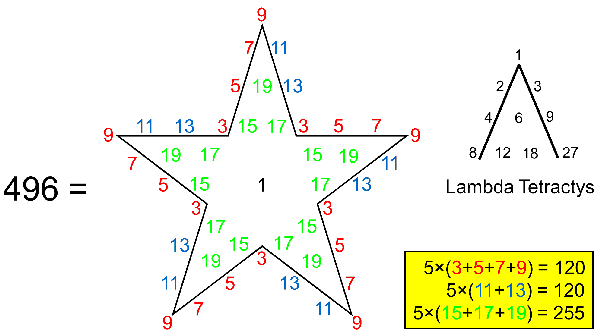
Notice that the six odd integers that form each point of the star and add up to 48 are analogous to the six revolutions of each whorl of the shadow matter superstring that carry 48 gauge charges of E8′. The 20 red integers add up to 120, as do the 10 blue integers. The counterpart of this in the 240 corners of the eight triacontagons present in the E8 Coxeter plane projection of the 240 vertices of the 421 polytope are the 120 vertices of a 600-cell and the 120 vertices of a second, smaller 600-cell inside the former. As
102 − 1 = 3 + 5 + 7 +... + 19 = 99,
is the sum of nine odd integers and
1 + 5×99 = 496,
is the sum of (1 + 5×9 = 46) integers, we see that the dimension 496 of E8×E8′ can be represented by a pentagram whose points are tetractys arrays of the 10 odd integers 3-19. The 30 (=12+22+32+42) red & blue integers lining the pentagram add up to 240, where 240 = (1+2+3+4)×4!, and the 16 (=42) remaining integers add up to 256, where 256 = 44. The Pythagorean Tetrad expresses the arithmetic architecture of this representation of 496, which is also the sum of the cubes of the first four odd integers:
496 = 13 + 33 + 53 + 73.
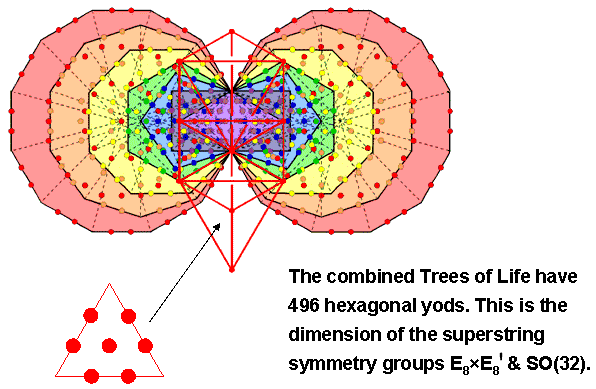
The distinction between the 30 numbers on the boundary of the pentagram and the 15 numbers that complete the five points as tetractys arrays of integers reminds one of the way in which Plato's Lambda (seven integers arranged along two sides of a triangle) is turned into the Lambda Tetractys when the three missing integers are added (see Figure 2 here). The outer Tree of Life with tetractyses as its triangles is composed of 16 tetractyses with 22 sides, so that its number of hexagonal yods = 22×2 + 16 = 60. The inner Tree of Life with Type A polygons has 444 hexagonal yods (see Table 10 here). The combined Trees of Life lose eight hexagonal yods when they combine (four hexagonal yods lining each side pillar), creating a total of 496 hexagonal yods that symbolise the 496 roots of both E8×E8′ and SO(32), the two symmetry groups required for superstring interactions that are free of quantum anomalies:
| << Previous 1... 15 16 [17] 18 19 ...24 Next >> |