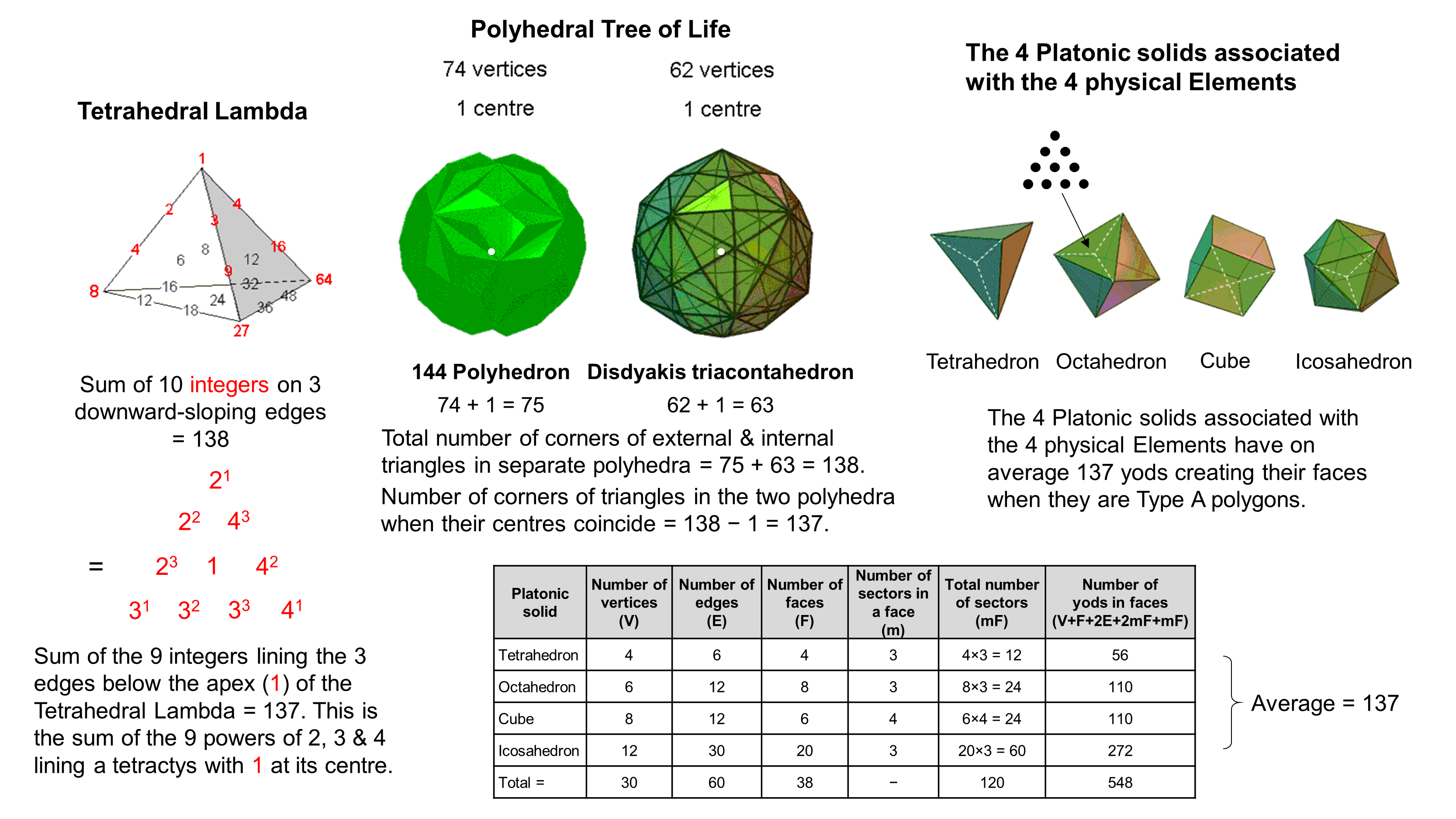
The Tetrahedral Lambda, the Polyhedral Tree of Life & the first four Platonic solids embody the holistic parameter 137.
| << Previous 1... 17 18 [19] 20 21 ...22 Next >> |
#19 The holistic parameter 137 parameterises the 10-d geometries of the shadow matter particle and the subquark
Elsewhere in this website (see here) we solved the longstanding mystery in physics of the significance
of the number 137 in determining the approximate magnitude of the dimensionless fine-structure constant, which
in the electrostatic cgs system is α = e2/ħc = 1/137.035999..... . It was the astronomer Sir Arthur
Eddington who wrongly conjectured in 1929 that its reciprocal was exactly 137, and he claimed to have explained
its presence, as some others have done since, although none of their efforts has received general acceptance by
physicists. We pointed out that the number must appear in the scientific account of the properties
of matter because we have demonstrated through many examples that it is a parameter of all holistic systems —
and the basic particles of matter are holistic systems. Before examining how this number manifests in the
dimensional geometry of the shadow matter particle and the UPA/subquark, we shall discuss briefly various
representations of holistic systems that embody it.
 |
|
The Tetrahedral Lambda, the Polyhedral Tree of Life & the first four Platonic solids embody the holistic parameter 137. |
Tetrahedral Lambda
The Tetrahedral Lambda discussed earlier is the tetrahedral array of 20 musical number weights generated by
considering the Lambda Tetractys as but the first of the four faces of a tetrahedron, the seven powers of 2 & 3
that line the two edges of this face being supplemented by three powers of 4 arranged along the third inclined edge
of the tetrahedron. The sum of the (3+7=10) red integers lining these three edges is 138. This is the number of
yods needed to construct the two joined, Type A dodecagons - the last of the seven types of regular polygons making
up the inner form of the Tree of Life, starting with their root edge. This is because each dodecagon has
73 yods (69 outside the root edge and 68 surrounding its centre). The number 68 will reappear
later when we discuss how the number 137 expresses the dimensional geometry of the shadow matter particle and the
UPA/subquark. The sum of the nine red integers below the apex (1) is 137. It is the
sum of these nine powers of 2, 3 & 4 when all 10 integers form a tetractys with 1 at its centre.
Polyhedral Tree of Life
The 144 Polyhedron has 74 vertices, 216 edges & 144 faces. The disdyakis triacontahedron
has 62 vertices, 180 edges & 120 faces. Together, they constitute the "Polyhedral Tree of
Life" (see here). The 144 Polyhedron is the polyhedral counterpart of the inner
Tree of Life, whose (7+7) enfolded polygons have 94 sectors with 74 corners unshared with the triangles of the
outer Tree. The disdyakis triacontahedron is the polyhedral counterpart of the latter. Joining all vertices of
each polyhedron to their respective centres creates (216+180=396) new triangles which, together
with the (144+120=264) triangles in their faces, generates (396+264=660) triangles with
(1+74+1+62=138) corners. The number 138 is the sum of the 10 musical number weights on the
three edges of the Tetrahedral Lambda that meet at the vertex with the number 1 assigned to it. If we imagine
one polyhedron placed inside the other (it does not matter to our discussion which one), with their centres
coinciding, there are now 137 corners. This is the sum of the nine integers below the apex of the Tetrahedral
Lambda with the number 1. Appropriately, this apex corresponds to the commmon centre of the two polyhedra,
whilst the nine integers lining edges that add up to 137 correspond to the 137 vertices that surround it.
4 Platonic solids
The ancient Greeks thought that particles of the Element
Fire had the shape of the tetrahedron, particles of Air had the shape of the octahedron, particles of Water had the
form of the icosahedron and particles of Earth had the shape of the cube. The table shown above shows that, when
their 38 faces are Type A polygons, their 120 sectors have 548 yods. On average, a Platonic solid representing a
physical Element has (548/4=137) yods in its faces. The tetrahedron has 56 yods in its faces, contributing
(56/4=14) yods to this average number, the octahedron & cube have 220 yods, contributing 55 yods to the
average, and the icosahedron has 272 yods, contributing 68 yods to the average number. The numbers 14, 55 & 68
have their counterparts in the sum of the nine integers on the three edges of the Tetrahedral Lambda that meet at
the apex to which the number 1 is assigned:
2 + 4 + 8 = 14;
3 + 9 + 27 + 16 = 55;
4 + 64 = 68.
The sceptic may choose to regard these detailed parallels as combinations that could arise by chance. But he cannot dismiss in the same fashion the property of the average Platonic solid having a yod population of 137 because this view is not plausible to any reasonable person — it stretches coincidence beyond its reasonable limits.
 |
| Analogous patterns in the yods in the faces of the average Platonic solid and the spatial coordinates of the shadow matter particle & subquark. |
Geometries of the shadow matter particle & the subquark
Let us now
consider the five whorls of the shadow matter particle described by Ron Cowen and the 10 whorls of the UPA that
Besant & Leadbeater discussed. The location of a point in n-dimensional space is defined by n numbers, or
spatial coordinates. Any curve is described by a mathematical function of these n variables. The whorls of both the
shadow matter particle and the UPA are closed curves in 10-d space. As they are confined to one of two parallel
space-time sheets separated by a gap extending along the 10th dimension, either coordinate measured along the
coordinate axis pointing along this dimension remains constant, whatever the values of the nine other coordinates
of a point on a whorl. But they will always be different for points on a whorl of the two types of particles
because neither type of superstring can move along the line segment connecting the two sheets. No oscillations of
each whorl penetrate this gap. Points on the five closed, 9-d curves comprising the shadow matter particle are
defined by (5×9=45) coordinates (see diagram). Each whorl has the same coordinate in the 10th dimension because the
E8-singlet states of the E8×E8′ heterotic superstring are confined to a space-time
sheet perpendicular to the coordinate axis pointing along this dimension. Although they have
50 coordinates in total, five must have the same value, and therefore these
50 numbers can have at most (50−4=46) different values. For the sake of
convenience, these numbers will be referred to as "spatial coordinates" even though it is their magnitude that is
meant. They can also be thought of as the spatial coordinates that are independent of one another,
i.e., "free variables." Points in whorls moving in either space-time sheet have coordinates measured in the tenth
dimension whose values are all the same and are unchanged by their motion on the sheet, so they represent only
one independent coordinate, not five. Similarly, points on the 10 whorls of the UPA are defined by a
maximum number of (10×9 + 1 = 91) independent coordinates. Therefore, (46+91=137) different numbers are need at
most to define points on the 15 whorls of both particles. This is a parameter of holistic
systems and their representations. It is evidence that the two particles constitute a holistic system. We saw
earlier that the UPA is the microscopic realisation of the disdyakis triacontahedron and that the shadow matter
particle is the realisation of the 144 Polyhedron, both polyhedra being composed of triangles in their faces and
interiors that have 137 corners when they are concentric. 15 is the number value of YAH
(יה), the older version of
the Godname of Chokmah, the letter value 5 of H (ה) being the number of whorls in the shadow matter particle and the letter value 10
of yod (י) being the number of whorls in the UPA.
SHADDAI EL CHAI prescibes the UPA and Cowen's particle
Confined to their 10-d space-time sheets, the two basic constituents of physical matter are the result of
15 dimensions of 26-d space-time becoming compactified. A point in this
space-time has 25 spatial coordinates, of which one specifies the location of the 10-d space-time sheet also
occupied by the point. Therefore, it has 24 variable coordinates. Points lying on the
15 whorls of both particles have (15×24=360) such coordinates. The two fixed
ends of the line segment between the two sheets and the time coordinate common to both particles constitute the
final three coordinates. The total number of variable space-time coordinates of the 15 whorls
= 360 + 3 = 363. This is the gematria number value of SHADDAI EL CHAI ("Almighty Living God"), the
complete Godname of Yesod. The three major whorls of the UPA have (3×6=18) coordinates associated with the six
compactified, superstring dimensions. The five whorls of Cowen's particle have (5×6=30) coordinates associated with
these dimensions, i.e., 31 coordinates associated with the seven compactified dimensions of
11-d space-time. The number value of CHAI is 18 and the number value of EL is 31.
Next, let us examine the various types of coordinates in more detail. Three of the nine dimensions of the 10-d space-time of superstrings refer to the large-scale space of 4-d Minkowski space-time and six are compactified, extending over only minute distances. An upper limit of 91 numbers define the positions of points on the 10 closed curves of the UPA (as already pointed out, we will call them "spatial coordinates," although it must be recognised that they are really the magnitudes of (10×10=100) Cartesian coordinates, 10 of which have the same value because they refer to 10 points on the same 10-d sheet). Therefore,
91 = 10×3 + 10×6 + 1 = 30 + 60 + 1
and
46 = 5×3 + 5×6 + 1 = 15 + 30 + 1,
so that
46 + 91 = 137 = 1 + 1 + 15 + 30 + 30 + 60 = 17 + 30 + 30 + 60.
Compare this result with the various types of yods making up the Type A polygonal faces of the first four Platonic solids. The calculations in the diagram shown above indicate that, on average, a Platonic solid has 30 tetractyses in its faces with 17 corners, 30 hexagonal yods at centres of tetractyses, 30 hexagonal yods on its 15 edges and 60 hexagonal yods lining internal sides of tetractyses. No such polyhedron exists, of course, but that is beside the point because we are interested only in what properties the four Platonic solids possess on average. Hence, the average number of yods in their faces = 17 + 30 + 30 + 60 = 137. But this is precisely the same set of integers as those found earlier to be the numbers of the various types of "coordinates" of points on the 15 closed curves of the shadow matter particle and the subquark! The same pattern of numbers exist in this context because we are considering a superstring, which is a holistic system that exhibits the same archetypal patterns, whatever form it takes.
The 17 coordinates we have just encountered are the coordinates in the 10th dimension of the two space-time sheets containing the two types of E8×E8' heterotic superstring and the 15 large-scale coordinates of the five whorls of the shadow matter particle. What corresponds in the 17 corners of tetractyses on average in the faces of a Platonic solid to the two coordinates of the former? The breakdown in the 68 corners in the faces of the four Platonic solids is:
Tetrahedron: 4 vertices + 4 face-centres;
Octahedron: 6 vertices + 8 face-centres;
Cube: 8 vertices + 6 face-centres;
Icosahedron: 12 vertices + 20 face-centres.
Either the tetrahedron providing eight corners, the octahedron with eight face-centres or the cube with eight vertices could — in their contribution to the average number of corners — provide the analogy with the coordinates of the two space-time sheets spaced along the 10th dimension of space. However, although any one of these is arithmetically possible, why should the corners in the faces of a particular Platonic solid be associated with these two coordinates, which are different from all the others because they are unchanging during the motion of the superstring? Given that we are considering four Platonic solids and that the numbers refer to averaging over all of them, there is the possibility that the eight corners in question are pairs of vertices from each polyhedron (all diametrically opposite except for the tetrahedron). Intuitively speaking, this choice seems preferable because it does not differentiate between the types of Platonic solids by picking out a particular one to be associated with the two coordinates of the space-time sheets. In the diagram above we call the pair of vertices "poles", in analogy to the North and South poles of the Earth. They correspond to the ends of the line segment that is the 10th dimension of space. The remaining 15 corners correspond to the 15 large-scale coordinates of the five whorls of the shadow matter particle. The diagram indicates the correspondences between the average numbers of the three other types of yods and the three other types of spatial coordinates.
Polygonal counterparts of the spatial coordinate patterns
In the Type B n-gon, 10n geometrical elements surround its centre. The 10 geometrical elements per sector comprise
three triangles and seven corners & sides, one of which is the corner of the n-gon and six of which are sides.
This 3:1:6 division is the same as that in the number of spatial dimensions predicted by M-theory, namely, three
large-scale dimensions, one line segment/circle and six compactified dimensions. This means that the Type B
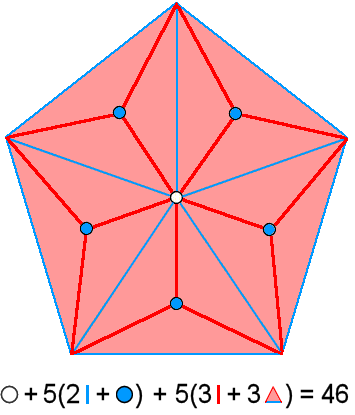
pentagon comprises (including its centre) 51 geometrical elements, that is, 46 geometrical elements other its five
corners, and that the Type B decagon comprises 101 geometrical elements, that is, 91
geometrical elements other than its 10 corners. There are (46+91=137) geometrical elements other than their corners
in the 15 sectors of these two polygons. This compares with the 137 spatial coordinate
variables of the 15 closed curves in the shadow matter particle and the subquark, the former
having 46 such coordinate variables and the latter having 91 variables:
|
E8-singlet state of E8×E8' (shadow matter particle) |
|
 |
|
Number of spatial coordinates of points in 5 whorls = |
Number of geometrical elements other than corners = |
|
|
E8'-singlet state of E8×E8' (UPA/subquark in up/ |
 |
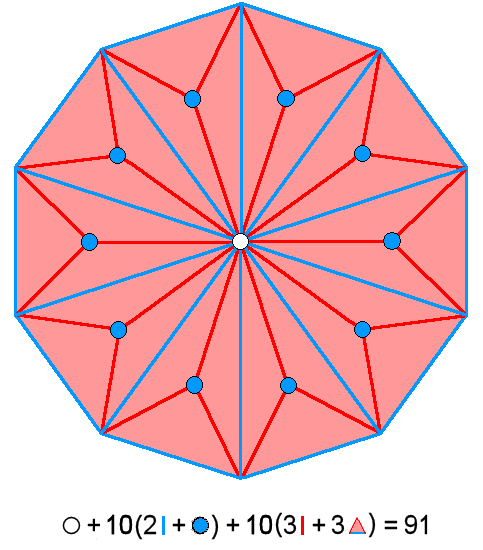 |
| Number of spatial coordinates in 10 whorls = 1 + 10×3 + 10×6 = 91 |
Number of geometrical elements other than corners = 1 + 10×3 + 10×6 = 91 |
|
| Total = | 137 spatial coordinates | 137 geometrical elements other than corners |
As confirmation that this correspondence is not coincidental, the diagram shown above reveals that it extends to the very numbers of geometrical elements that are either in the Type A polygon or added when it is Type B. The following parallels exist:
|
spatial coordinate |
geometrical element |
|
| space-time sheet |
→ |
point: centre of polygon; |
| 2 transverse in large scale, 3-d space |
→ |
line: 2 sides of sectors; |
| 1 longitudinal in large-scale, 3-d space | → | point: centre of sector; |
| 6 compactified dimensions | → | lines & triangles: 3 sides + 3 triangles = 6 lines & triangles. |
The Type B pentagon represents the pattern of coordinates in the five closed curves of the shadow matter particle and the Type B decagon represents the pattern in the 10 closed curves of the UPA/subquark. Each one of their sectors corresponds to a curve/whorl and each geometrical element of a given type corresponds to a certain class of spatial coordinate of a point in each curve/whorl.
The number of SLs in the n-Tree = 6n + 5. Hence, the 7-tree has 47 SLs and the 22-tree has 137 SLs. There are 91 SLs from the top of the 22-tree to the top of the 7-tree mapping the physical plane in CTOL. This property relates the Kabbalistic number 22 (number of Paths in the Tree of Life) to the number 137 associated with the fine-structure constant at the heart of theoretical physics.
The numbers 46 and 91 are embodied in the Tetrahedral Lambda because the numbers 27 (=33) and 64 (=43) located at two vertices add up to 91, whilst the sum of the seven other numbers 2, 4, 8, 3, 9, 4, & 16 on the three edges meeting at the apex with the number 1 is 46. These numbers are also embodied in the Type B triangle and the Type B hexagon because the number of yods in the Type B n-gon is 15n + 1, so that the former with n = 3 has 46 yods and the latter with n = 6 has 91 yods. What, however, makes the pentagon & decagon special is that their geometries are analogous in every detail to the pattern of spatial coordinates in, respectively, the shadow matter particle and the subquark. This is made possible by the crucial fact that there are (per sector) nine geometrical elements other than polygonal corners that are analogous to the nine spatial dimensions in which E8×E8' heterotic superstrings move. When all the 14 polygons in the inner Tree of Life are Type B, they contain 1370 yods, i.e., the yods in 137 tetractyses (see here)! We see that the famous number 137 is embodied in the complete inner form of the Tree of Life, as well as in two of its polygons. These two polygons are unique also because the Golden Ratio Φ appears in their geometry. For example, the ratios of the lengths of various pairs of red & blue lines (taking the lengths of the latter as 1) in the pentagon enclosing a pentagram are all equal to Φ:
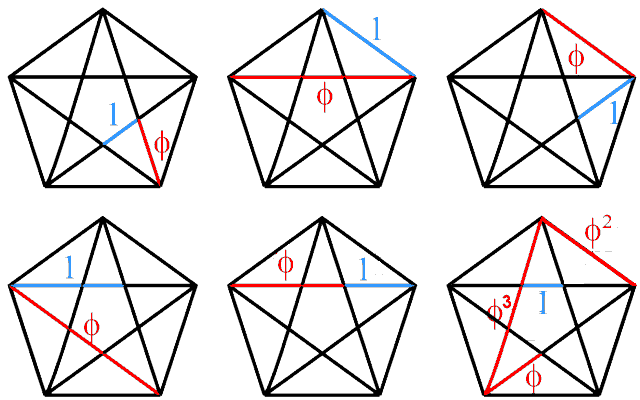
The Type A pentagon is a geometrical representation of the Divine Name EHYEH ("I am") associated with Kether, the first Sephirah, because its five sectors have 21 points, lines & triangles, where 21 is the gematria number value of this Godname. The one centre, five corners, 10 sides & five triangles express the number values of the Hebrew letters in AHIH because A = 1, H = 5 & I = 10. Constructed from tetractyses, the Type A pentagon has 31 yods, its centre and the 30 yods surrounding it corresponding, respectively, to the number value 1 of E and the number value 30 of L in the Divine Name EL ("God") assigned to Chesed. The Type B pentagon has 76 yods (26 yods lining its sectors, inside which are 50 yods), where 76 is the number value of YAHWEH ELOHIM. The Godname YAHWEH has the number value of 26 and the Godname ELOHIM has the number value of 50. The Type B decagon has 151 yods, where 151 is the 76th odd integer. It comprises 101 geometrical elements, where 101 is the 26th prime number.
| << Previous 1... 17 18 [19] 20 21 ...22 Next >> |