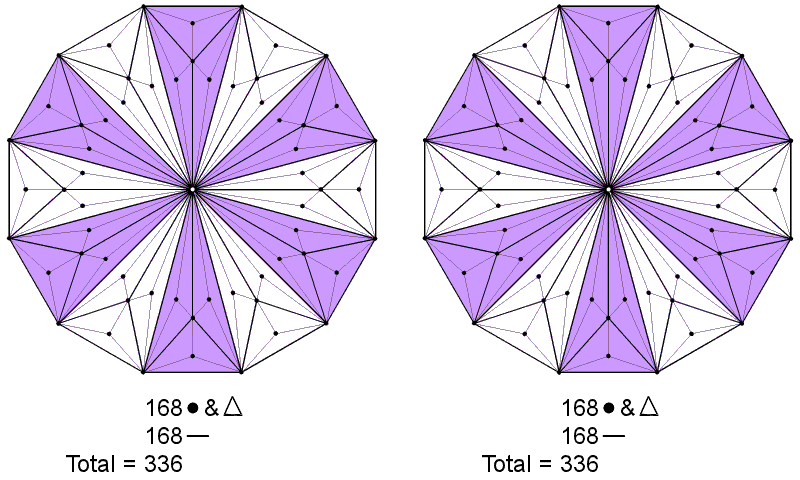
672 geometrical elements surround the centres of two Type C dodecagons.
The 12th dodecagonal number is 672.
| << Previous 1... 11 12 [13] 14 15 ...22 Next >> |
#13 The superstring structural parameter 672 as the 12th dodecagonal number
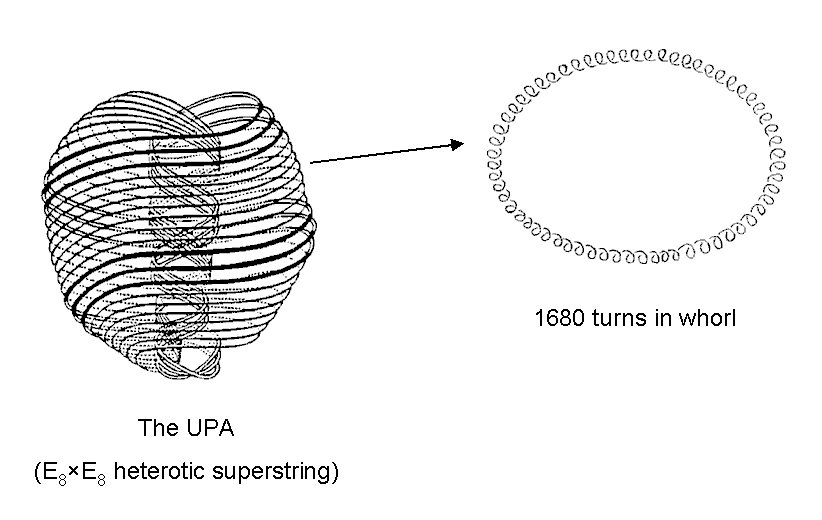
It was shown earlier in this section that every revolution of a helical whorl of the UPA or shadow matter particle is composed of 336 circular turns, where
336 = 4×84 = 22(12 + 32 + 52 + 72) = 22 + 62 + 102 + 142
is the sum of the squares of the first four even integers that are four units apart. This illustrates the Tetrad Principle (see Article 1) at work, expressing this fundamental structural parameter of E8×E8′ heterotic superstrings. Each turn is a circularly polarised oscillation made up of two perpendicular plane waves oscillating 90° out of phase. Every revolution is a superposition of (2×336=672) such sinusoidal waves. The 2016 turns of a whorl of the shadow matter superstring consist of (2016+2016) plane waves. Their inner Tree of Life counterpart are the (2016+2016) yods surrounding the centres of the (7+7) Type C polygons (see #3). The 42 yods per sector of a Type C polygon comprise six classes of seven yods. Each class determines one revolution of 336 turns, which are denoted by the (48×7=336) yods in each class for all seven Type C polygons. The 672 plane waves making up each revolution are symbolised by the (336+336=672) yods in each class for the (7+7) Type C polygons. We saw in #3 that the same (336+336) pattern exists in the geometry of the (7+7) Type B polygons as the (336+336) corners & sides surrounding their centres, as well as in the four Platonic solids, when constructed from tetractyses, associated with the four Elements of Fire, Air, Water & Earth as the 336 yods in each set of their halves. There are also 672 yods surrounding the centres of each half of the inner Tree of Life with Type B polygons that are unshared with the outer Tree of Life. The presence of this number in various sacred geometries is indicative of its status as a defining parameter of holistic systems. This is confirmed by the fact that there are 6720 (=672×10) edges in the 421 polytope, whose 240 vertices represent the 240 roots of the rank-8 Lie group E8 appearing in E8×E8′ heterotic superstring theory.
The dodecagon is the polygonal form of the Tree of Life (see here). The number of points, lines & triangles surrounding the centre of the Type C n-gon = 28n. For the Type C dodecagon (n=12), this is 336. Hence, the two Type C dodecagons present in the inner Tree of Life have (336+336=672) geometrical elements surrounding their centres:
 |
 |
|
672 geometrical elements surround the centres of two Type C dodecagons. |
The 12th dodecagonal number is 672. |
This demonstrates the archetypal nature of the number 672 embodied in the geometry of the fourth type of dodecagon:
| 1. Dodecagon | 2. Type A dodecagon | 3. Type B dodecagon | 4. Type C dodecagon |
and it serves to illustrates the Tetrad Principle, discussed in Article 1, whereby the fourth member of a class of mathematical objects embodies numbers that are parameters of holistic systems.
The class of numbers called "polygonal numbers" is discussed in the Polygonal numbers section. The nth polygonal number of order N is
PNn = ½n[(N−2)n − (N−4)].
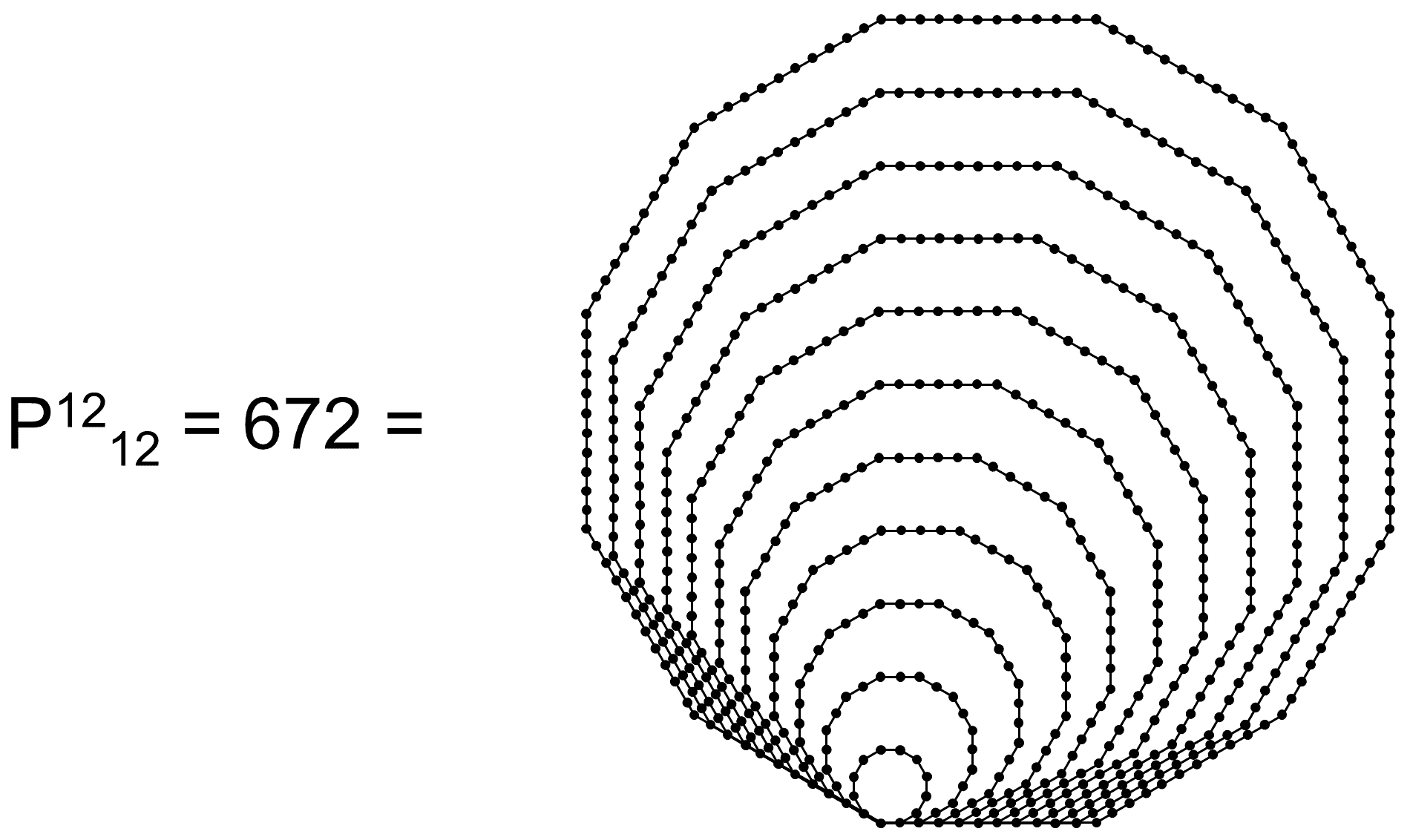
The nth dodecagonal number is P12n ≡ dn = n(5n−4). Therefore, d12 = 672 (see the diagram above on the right). Just as the Type C dodecagon embodies in its geometry the number 672, so the 12th dodecagonal number is this number as well! Table 2 in the Polygonal numbers section indicates that 336 is not a polygonal number. Nor are the numbers 168, 1680 and 2016. The number 672 is the only fundamental, superstring structural parameter that is also a polygonal number. Given that:
the number 672 is the 10th of the non-trivial dodecagonal numbers larger than 12:
| n = |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
dn = |
|
|
|
|
|
|
|
|
|
|
|
|
It consists of 11 nested dodecagons with 11 shared corners and (11×11=121) separate corners, i.e., a total of 122 different corners. This is the number of yods in two separate Type A decagons because each has 61 yods. There remain (672−122=550) dots lining sides, where
550 = 10×55 = 10(1+2+3+4+5+6+7+8+9+10),
i.e., 550 is 10 times the 10th triangular number. Remarkably, this number is the number of SLs in CTOL (see here). We see that the Decad determines the holistic parameter 672 because
These properties show how the number 10 determines the number of plane wave components of the 336 circularly polarised oscillations in one revolution of a whorl of both the E8-singlet shadow matter particle remote-viewed by Ron Cowen in 1991 and the subquark state of the E8′-singlet sector of E8×E8′ heterotic superstrings, namely, the UPA that was remote-viewed by C.W. Leadbeater 127 years ago. They demonstrate the universal character of this structural parameter of superstrings, and they explain why it manifests in sacred geometries (for example, see pages 15-20 at Polychorons & Gosset polytope), for these religious objects are isomorphic blueprints of reality, including the vibrational excitations of the fabric of space-time called "superstrings." As
168 = 132 − 1 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25
is the sum of the first 12 odd integers after 1,
672 = 4×168 = 12 + 20 + 28 + 36 + 44 + 52 + 60 + 68 + 76 + 84 + 92 + 100
= (12+100) + (20+92) + (28+84) + (36+76) + (44+68) + (52+60) = 336 + 336.
In other words, starting with 12, the 12 successive, even integers that are eight units apart add up to 672 and divide into two sets of six integers that add up equally to 336, mirroring the fact that the 672 plane waves comprise 336 orthogonal pairs of waves oscillating a quarter of a cycle apart. Once more, this arithmetic property reveals the special significance of the number 12 to the number 672.
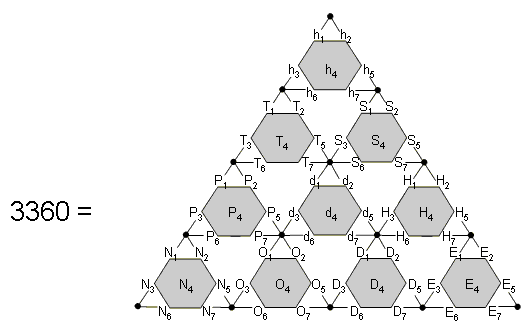
The nth orders of the 10 polygonal numbers that correspond to the first 10 types of regular polygons, seven of which make up the inner Tree of Life, are: P3n = Tn, P4n = Sn, P5n = Pn, P6n = Hn, P7n = hn, P8n = On, P9n = Nn, P10n = Dn, P11n = En & P12n = dn. The polygonal number hn corresponds to the heptagon, the polygonal number Nn corresponds to the nonagon and the polygonal number En corresponds to the undecagon. These polygons are absent from the inner form of the Tree of Life. The 10 1st-order tetractyses that make up the 2nd-order tetractys contain (10×7=70) hexagonal yods arranged at the centres and corners of 10 hexagons. Let us assign the first seven orders of polygonal numbers corresponding to the three absent polygons to the hexagons in the 1st-order tetractyses at the three corners of the 2nd-order tetractys. Then, suppose that we assign the first seven orders of polygonal numbers corresponding to types of polygons in the inner Tree of Life to the hexagons in the seven remaining 1st-order tetractyses. The sum of these 70 polygonal numbers is 3360:
 |
 |
|
The sum of the first seven orders of the first 10 polygonal numbers is 3360. |
1680 circularly polarised oscillations (3360 plane waves) make up each helical whorl of the UPA. |
As 3360 = 1680×2, this is the number of plane waves making up the 1680 turns of each whorl of the UPA. Alternatively, it is the number of turns making up one revolution of the 10 helical whorls of the UPA, for each whorl makes five revolutions around the axis of the UPA and each revolution comprises 336 turns. As 3360 = 336×2×5, there are 3360 sinusoidal oscillations in each revolution of the five whorls of the shadow matter particle. Is it just coincidence or is it mathematical design that this connection between the superstring structural parameter 336 and the first 10 polygonal numbers should exist? It seems highly improbable that the relevance of the number 3360 to three oscillatory features of these two particles could be due to the former.
The 2nd-order tetractys is the Pythagorean counterpart of the Kabbalistic Tree of Life as a representation of holistic systems, being isomorphic to it:
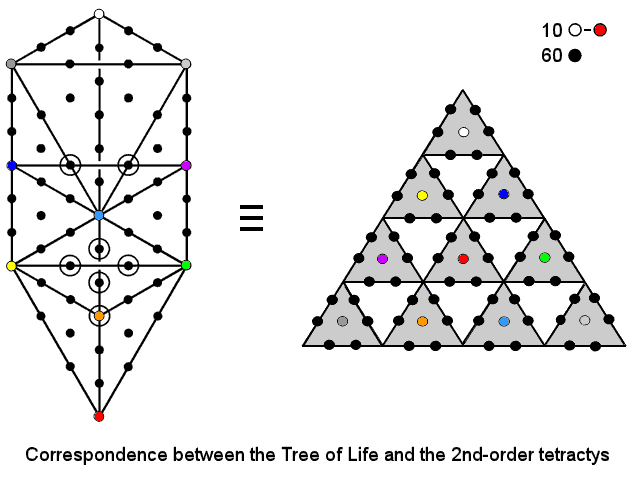
The 70 polygonal numbers could have been assigned to the 70 yods that make up the outer Tree of Life when its 16 triangles are regarded as tetractyses, and their sum would have been the same. Their mathematical property of having the predicted superstring structural parameter 3360 as their sum is therefore as much Kabbalistic as it is Pythagorean. It exists not by chance but because the number 70 is, as well, a defining parameter of holistic systems and all their sacred-geometrical representations. For example, each set of halves of the five Platonic solids have 70 vertices & edges, whilst the 43 triangles in the 2-dimensional Sri Yantra contain 70 points that include its point of origin, or bindu (see here). One would rightly be sceptical about a claim that the number 3360 had archetypal significance if all the polygonal numbers adding up to it had been selected at random. But this is not the case here. Instead, both the number and the make-up of the 70 polygonal numbers as the first seven orders of the first 10 polygonal numbers reflect the fundamental, Kabbalistic significance of the numbers 7 and 10. This property of the 7×10 polygonal numbers has an arithmetic counterpart that expresses yet another superstring structural parameter. As
712 − 1 = 70×72 = 5040 = 3×1680 = 3 + 5 + 7 +... + 141,
the sum of the first 70 odd integers after 1 is the number of turns in the three major whorls of the UPA, each of which carries 24 gauge charges of E8, 70 turns per charge. The number 5040 is also the number of turns in each half of the shadow matter particle, for each of its five helical whorls contains 2016 turns, a total of 10080. As 5040 = 7!, this number is the order of the permutation group of order 7.
Here is a list of some of the ways in which various sacred geometries embody the superstring structural parameters 336, 3360 and 672:
|
Sacred geometry |
336 |
672 |
|
336 corners & sides surround the centres of the 7 Type B
polygons. |
672 corners & sides surrround the centres of the (7+7) Type B
polygons. |
|
| Two Type C dodecagons (see also here). | 336 geometrical elements surround the centre of the Type C dodecagon. | 672 geometrical elements surround the centres of the two Type C dodecagons. |
| Two Type C octagons (see also here). | The Type C octagon has 336 yods surrounding its centre. | The two Type C octagons have 672 yods surrounding their centres. |
| 1st 4 Platonic solids (see here & here). | There are 336 yods in faces and interiors of each half of the 1st 4 Platonic solids. | There are 672 yods in the faces and interiors of the 1st 4 Platonic solids. |
| 3-d Sri Yantra (see also here & here). | 336 yods line its 42 triangles when they are tetractyses. | Its 42 Type A triangles have 672 yods other than their 84 corners because 672 = 16×42. |
| 24-cell (see also here and here). | 336 geometrical elements make up the faces of each half. | Its faces have 672 geometrical elements. |
| Disdyakis triacontahedron (see here). | 3360 vertices & hexagonal yods in each half surround its axis when edges and sides of sectors of faces are sides of internal Type A triangles. | 6720 vertices & hexagonal yods surround its axis when edges and sides of sectors of faces are sides of internal Type A triangles. |
| 421 polytope (see also here). | The faces in each half of the polytope have 3360 edges. | The faces of the polytope have 6720 edges. |
The two numbers parameterise these geometries so naturally that the listed examples offer a sceptic no justification for claiming that their appearances have been achieved artificially by cherry-picking properties of these geometrical objects. "Cherry-picking" means selecting a subset of the properties of an object without regard to their type/class merely to generate a collection of the desired number of them. Whatever its status as sacred geometry, that type of action is always possible, and no significant conclusion can be drawn from it. However, it is entirely a different matter when, despite the selection being restricted to certain types of objects or properties, the same number always turns up in each context, quantifying some global property, although, of course, not necessarily expressing the same types of properties. Tempted to shrug off any one appearance as due only to coincidence, the sceptic knows that his explanation of its appearance becomes highly improbable and therefore untenable if he tries to dismiss in similar fashion as many cases as the eight ones listed above, where the numbers manifest as global parameters of a system purportedly possessing sacred geometry. The cases share these (and other) numbers because, being sacred geometries, they must necessarily be isomorphic to one another and therefore be characterised by the same set of parameters. There is therefore no mystery why different sacred geometries embody the same numbers. Mathematical design, not chance, is what is responsible for their appearance.
We saw in #3 that the number 672 is the sum of the nine musical number weights lining the sides of a tetractys with the number weight 48 at its centre: 672 = 14×48. This number is also 28×24, so that it is the number of hours in the lunar month defined in English common law as 28 days (four weeks), although the astronomical lunar month (synodic month), defined as the period between successive new moons, is 29 days, 12 hours, 44 minutes & 3 seconds. The number 336 is the number of hours in a fortnight and the number 168 is the number of hours in a week. As 2016 = 3×672 and 1680 = 2½×672, the number of circularly polarised waves in the shadow matter particle happens to be the number of hours in three such lunar months, whilst the corresponding number in a whorl of the UPA is the same as the number of hours in 10 weeks, or 2½ months, as legally defined in the United Kingdom. As far as the author is aware, neither of these periods of time is an astronomical or human cycle of some kind. Perhaps a more relevant parameter is the number 6720 = 2×3360, which is the number of plane wave oscillations making up one revolution of all 10 whorls of the UPA. As has been noted previously, this is the number of edges of the (9×6720=60480) faces of the 421 polytope whose 240 vertices represent the 240 roots of E8 (see Table 1 here). The number factorises as 24×28×10 = 24×280, where 280 is the number value of Sandalphon, the Archangel of Malkuth. It is the number of hours in 280 days. Compare this with the fact that human pregancy lasts for about 280 days, or 40 weeks. This is the average length of gestation from the first day of the woman's last menstrual period. Most babies are born between 38 and 42 weeks of gestation. Admittedly, this period represents only an average figure. Despite this, it remains curious (and perhaps more than coincidence) that the two numbers are identical, particularly as their factorisations are the same as well, remembering that earlier analysis indicated that each one of the 240 E8 gauge charges is spread over 70 turns of a helical whorl of the UPA, each carrying 24 gauge charges that are spread around its 1680 turns:
Number of oscillations per revolution of 10 whorls = (24×10 gauge charges×70 turns×2)/5
revolutions = 24×280 = 6720;
Number of hours in the average human gestation period = 24×280 = 6720.
It is as though each normal 28-day menstrual cycle lasting 672 hours corresponds to a different whorl of the UPA, for in either case there are 10 of them. Apart from an extra factor of 10, the same factorisation manifests in the geometrical composition of the 421 polytope, whose 9×6720 triangular faces have 6720 edges, i.e., its number of edges & faces = (9+1=10)×6720 = 67200 = 10×24×280.
The Tetrad expresses the factorisation 70×24 of 1680 as
|
1680 = |
﴾ |
4 + 4 |
﴿ |
4! |
|
4 |
i.e., as the number of permutations of any four objects selected from a set of eight objects. Geometrically, this is the number of ordered 3-simplexes in a 7-simplex, there being
|
70 = |
﴾ |
8 |
﴿ |
3-simplexes formed by the 8 vertices of a 7-simplex, each one having (4!=24) orderings of its four vertices.* The total number of objects making up these 1680 permutations of eight objects selected four at a time = 4×1680 = 6720. This number is:
The same number appears in them not as a result of chance but because all holistic systems, such as a human being and the subquark state of the E8×E8′ heterotic superstring, are characterised by the same set of global parameters. As the ancient Pythagoreans understood, all forms represent numbers. The modern theoretical physicist would agree with this. But, unlike the latter, the former recognised that certain numbers are special in that they quantify the properties of an equally special class of objects: holistic systems, symbolised by the tetractys and its higher orders. The basic types of subatomic particles making up atoms have not yet been discovered by high-energy physics. When the UPA is detected inside quarks, the holistic nature of matter revealed in this website will be confirmed.
*An n-simplex is an n-dimensional polytope, which is the convex hull of its n + 1 points. It is the n-dimensional generalisation of the 0-simplex (point), 1-simplex (line segment), 2-simplex (triangle) & 3-simplex (tetrahedron).