#11 The yod population of the eight Type C triacontagons is the number of turns in the five helical whorls of the shadow matter superstring

We found in the previous page that there are 10080 hexagonal yods in the faces of the 30 disjoint 16-cells whose 240 vertices are the vertices of the compound of two 600-cells. This compares with the 10080 turns predicted to exist in the five helical whorls of the shadow matter superstring (an E₈-singlet state of the E₈×E₈′ heterotic superstring). En passim, we must emphasize that this number was not derived by any counting by Ron Cowen, the Canadian Buddhist clairvoyant who first described in the 1990s shadow matter with his micro-psi faculty. It was derived on page 1 by assuming that, just as the disdyakis triacontahedron embodies the structural parameter 1680 of the UPA in its geometry (the number of turns in each helical whorl), so the 144 Polyhedron —the other member of the Polyhedral Tree of Life — embodies the structural parameter 2016 as the number of turns in each of the five whorls of the shadow matter particles that Cowen described. Evidence supporting this theoretical prediction was presented in subsequent pages in the context of the inner Tree of Life, the Sri Yantra, the Tetrahedral Lambda, etc. It was argued that the correspondences between features of these particles reported by Cowen and the composition of 24-cells and 16-cells in each 600-cell are too detailed to arise just by chance. As further confirmation of this conclusion, we shall now show that regarding the triacontagons as Type C polygons leads to exactly the same factorisation

10080 = 30×336

as is implied by the Type A faces of every one of the 30 disjoint 16-cells in the two 600-cells having 336 hexagonal yods.

The number of yods in the nth-order m-gon is given by:

Y_n(m) = 1 + 3m(1+3ⁿ)/2.

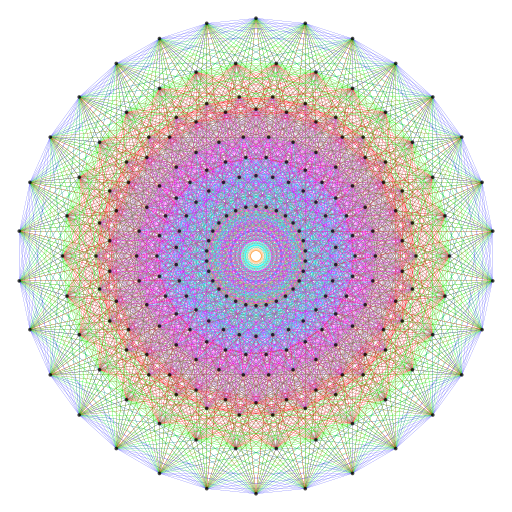
(for proof, see Table 9 in Article 65). The Type C m-gon (n = 3) has 42m yods surrounding its centre, and the Type C triacontagon (m = 30) has 1260 yods surrounding its centre, where 1260 is the gematria number value of Tarshishim, the Order of Angels assigned to the Sephirah Netzach. There are 42 yods per sector of a triacontagon: 1260 = 30×42. The E₈ Coxeter plane projection of the 240 vertices of the 4₂₁ polytope that represent the 240 non-zero roots of E₈′ is the 240 corners of eight concentric triacontagons:

The four triacontagons with 120 red corners shown above are the projection of the 120 vertices of the larger 600-cell; the four triacontagons with 120 blue corners are the projection of the 120 vertices of the smaller 600-cell. Each set of four triacontagons has 120 sectors with (120×42=5040=7!) yods. Each set corresponds to an outer or inner half of the shadow matter particle with 5040 turns of its five whorls making up three revolutions around its axis. The yod population of the eight Type C triacontagons is exactly equal to the number of turns in the five whorls of the shadow matter particle! Instead of the factorisation

10080 = 30×336

encountered when we considered the division of the two 600-cells into 30 disjoint 16-cells, we now have

10080 = 30×8×42.

The 30 sectors of a triacontagon comprise five sets of six sectors (coloured red, yellow, green, blue & violet in the diagram shown above). Each set contains (6×42=252) yods. The eight groups of six sectors of each colour in the eight triacontagons have (8×252=2016) yods. This is the number of turns in each whorl. The 240 sectors of the eight triacontagons consist of five sets of 48 sectors (six similarly coloured sectors repeated over the eight triacontagons). Each set with (48×42=2016) yods expresses a complete, helical whorl with 2016 turns. The five-fold symmetry of the triacontagon is responsible for the five distinct whorls making up the E₈-singlet state of the E₈×E₈′ heterotic superstring.

Here is unequivocal evidence of the oscillatory structure of the shadow matter superstring being encoded in the very geometry of the triacontagons formed by the vertices of the 4₂₁ polytope that represents the roots of E₈′. One could hardly ask for even more convincing evidence that the particle described by Cowen is the E₈×E₈′ heterotic superstring. Nevertheless, for those who want it, consider this: the number of geometrical elements in the nth-order m-gon is given by

G_n(m) = 1 + m(1+3ⁿ)

(for proof, see Table 9 in Article 65). The Type C m-gon (n = 3) has G₃(m) = 28m geometrical elements surrounding its centre, so that the Type C triacontagon has G₃(30) = 840 geometrical elements surrounding its centre. There are (8×840=6720) geometrical elements surrounding the centres of the eight Type C triacontagons. Compare this with the property of the 4₂₁ polytope having 6720 edges. Exactly the same number appears in the basic geometrical description of the parent polytope. Admittedly, this number does not refer to the same property, for we are considering the 4-dimensional projection of the 4₂₁ polytope, not the polytope itself. But that is beside the point and does not nullify the significance of its appearance. Readers must ask themselves: what is the likelihood of this number appearing by chance in two different (albeit related) contexts, one being the geometrical shape of the 4₂₁ polytope (known for 120 years) and the other being a mathematical transformation of polygons conceived by the author for general application to sacred geometries and applied here to the H4 Coxeter plane projection of this polytope? There is no sense in which this appearance could be manufactured, i.e., be artificial, for the Type C polygon is just one member of a mathematically well-defined, infinite family of nth-order m-gons, and this website provides many other examples of these first three types of transformations (n = 1, 2, 3) of polygons embodying holistic parameters. Therefore, the appearance in the analysis of the number 6720 as one such parameter is nothing exceptional (and, certainly not contrived), although no less remarkable than others. Notice that 6720 = 4×1680 and 10080 = 6×1680, so that this number is, simply, the extra number of turns the UPA with (10×1680=16800) turns in its 10 whorls has relative to the number (10080) of turns predicted for the shadow matter particle described by Cowen!:

10080 + 6720 = 16800.

The numbers of turns in the UPA and the shadow matter particle form a tetractys pattern of numbers 1680 with the number of edges of the 4₂₁ polytope:

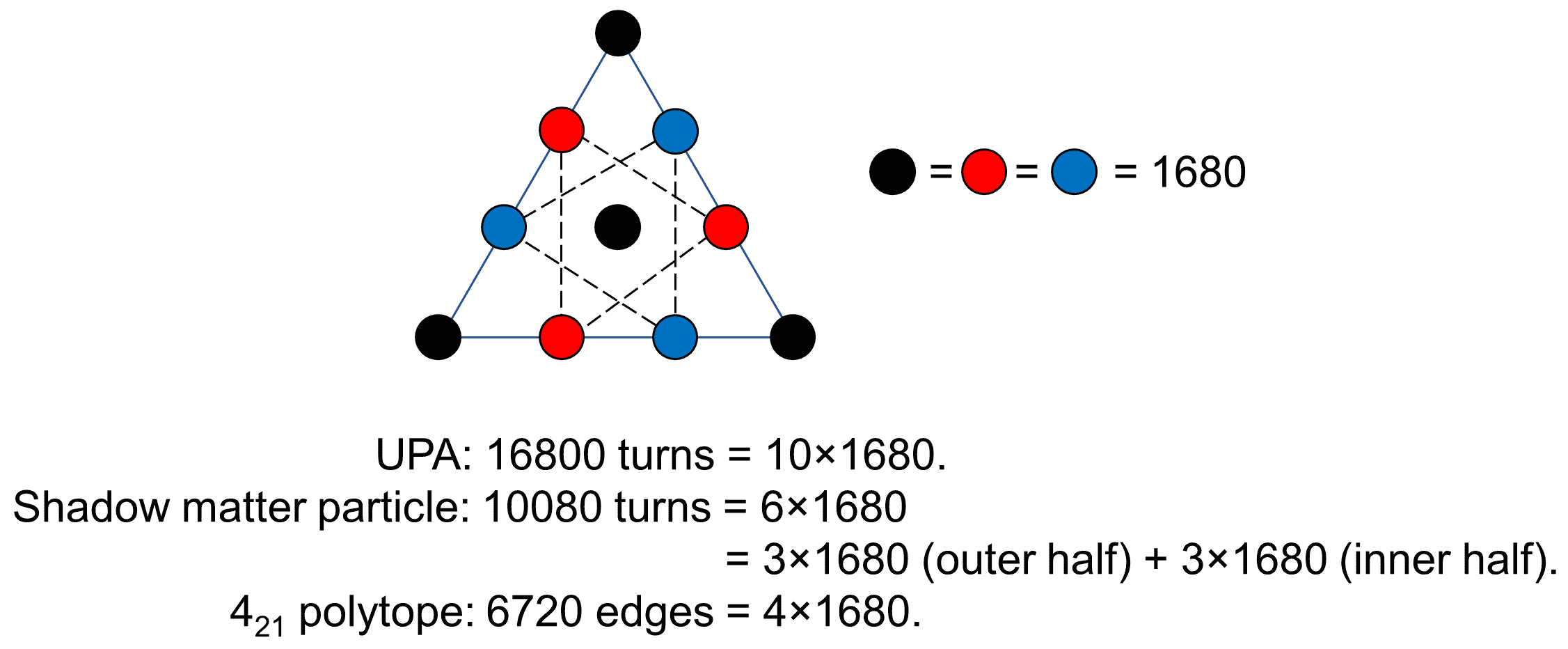The shadow matter particle, Gosset polytope & UPA conform to the holistic paradigm of the tetractys.	10080 circularly polarised oscillations make up the shadow matter particle.	The Gosset polytope has 6720 edges.	16800 circularly polarised oscillations make up the UPA (subquark member of the E8′-singlet sector of the E8×E8′ heterotic superstring).

The two sets of three red/blue hexagonal yods weighted with the number (1680) of turns in a whorl of the UPA express the 5040 (=7!) turns in the inner or outer halves of the shadow matter particle. Once again, we ask: what is the likelihood that this geometrical parameter of an eight-dimensional object representing the roots of a Lie symmetry group present in superstring theory should so simply — yet merely by chance — relate two numbers at the heart of alleged, paranormal observations of subatomic particles? How many miracles of coincidence can a sceptic tolerate before he or she has to admit that profound, mathematical design — not chance — is revealing itself here? If the equation highlighted above is divided on each side by 336 (the number of turns per revolution of a whorl), it becomes

30 + 20 = 50.

This is merely a statement that the 50 revolutions of the 10 whorls of the UPA comprise 20 more revolutions than the 30 revolutions of the five whorls of the shadow matter particle. The miracle, of course, is that, in terms of turns of helical whorls, the difference of (20×336=6720) is exactly equal to the number of edges of the 4₂₁ polytope, whose 240 vertices represent the 240 roots of E₈, which is the unified symmetry group of the UPA, once it is interpreted as the subquark state of the E₈′-singlet sector of E₈×E₈′ heterotic superstrings! Does the sceptic really need to be shown the theoretical reason for this before he finally admits that his attempt to dismiss it as coincidence so that he does not have to accept that superstrings have been remote-viewed lacks plausibility?

<< Previous    1...   9  10  [11]  12  13  ...20    Next >>

Home