| << Previous 1... 8 9 [10] 11 12 ...24 Next >> |
#10The 30 16-cells in the compound of two 600-cells embody the shadow superstring structural parameter 10080
The 421 polytope is the 8-d polytope whose 240 vertices represent the 240 roots of E8. The way in which its geometry and that of its various polychorons are isomorphic to sacred geometries and are related to the structure of the UPA is discussed in the section 4-d sacred geometries, knowledge of which will be assumed in the analysis that follows here. We shall focus on the remarkable correspondences between these properties and the structure of the shadow matter superstring, which is the E8-singlet state of the E8×E8′ heterotic superstring, just as the UPA is its E8′-singlet state — or, more accurately, the ground state of the subquark member of a multiplet of such states.
 |
The 4-d projection in the H4 Coxeter plane of the 240 vertices of the 421 polytope creates two 600-cells, one inside the other and the larger scaled to the smaller in the proportion of the Golden Ratio. The Petrie polygon of the 600-cell is the triacontagon (see here). Its interior angle is 168°, which is the gematria number value of Cholem Yesodoth, the Mundane Chakra of Malkuth. The sum of the 30 interior angles is 5040, which is 7! This is the number of turns in each half of the shadow matter particle (see previous pages). Its five whorls make 30 revolutions around its axis of rotation, each half-revolution comprising 168 turns, just as the whorls of the UPA do. It is remarkable that such a correspondence between mathematical facts and alleged paranormal observations should exist and it is hard to defend the suggestion that it might be no more than coincidence. When such examples continue to accumulate, this type of sceptical explanation becomes highly implausible.
The 600-cell is a compound of five disjoint 24-cells, although it contains 25 24-cells and there are 10 ways of partitioning all its 120 vertices into five disjoint sets of 24. The 24-cell is a compound of three 16-cells, each consisting of four pairs of vertices with coordinate values 1 and −1 on the four perpendicular axes and joined by edges to one another except when the other vertex is diametrically opposite it. This is the geometrical basis for the factorisation of 120:
120 = 5! = 5×4×3×2×1.
The Petrie polygon of the 16-cell is the octagon. Its four opposite pairs of corners denote vertices of the 16-cell at 1 and −1 along each axis. As the compound of three 16-cells, the 24-cell has 24 vertices that can be divided into three sets of eight (three sets of four forming the larger dodecagon that is its Petrie polygon and three sets of four forming the smaller dodecagon). This 3×(4+4) pattern is analogous to the eight trigrams, which comprise two sets of four, corresponding members of each set having lines and broken lines reversed. Their counterpart are the eight sets of three vertices, paired together as four sets, in which triplets of vertices are paired with triplets of their complementary opposites in their 16-cell:
| (+, +, +) |
↔ |
(−, −, −) |
| (−, +, +) |
↔ |
(+, −, −) |
| (+, −, +) |
↔ |
(−, +, −) |
| (−, −, +) |
↔ |
(+, +, −) |
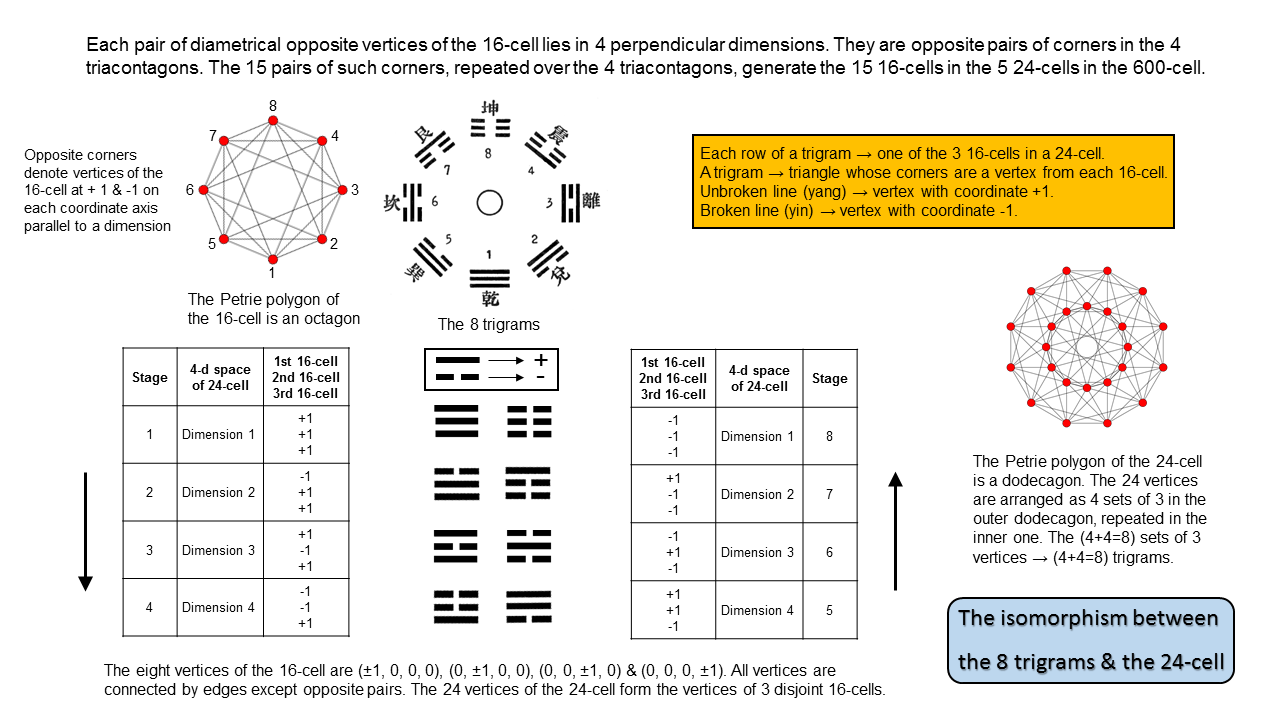 |
The two sets of four trigrams express the fact that a 16-cell consists of four vertices at (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0) & (0, 0, 0, 1) and their opposites at (−1, 0, 0, 0), (0, −1, 0, 0), (0, 0, −1, 0) & (0, 0, 0, −1). The three rows of each trigram express the fact that the 24-cell is the compound of three disjoint 16-cells.
The two tables shown below list the geometrical and yod composition of the six polychorons when their faces are Type A polygons and when internal triangles formed by their edges are Type A triangles (for details of their calculation, see here).
Geometrical composition of the faces
and interiors of the 6 polychorons.
(C/C′ = number of
external/internal corners; S/S′ = number of external/internal sides; T/T′
= number of external/internal triangles;
N/N′ = number of external/internal geometrical
elements; c/s/t/n = total number of
corners/sides/triangles/geometrical elements).
|
Polychoron |
Faces |
Interior |
Total |
|||||||||
|
|
C |
S |
T |
N |
C′ |
S′ |
T′ |
N′ |
c |
s |
t |
n |
|
5-cell |
15 |
40 |
30 |
85 |
1+10 |
35 |
30 |
1+75 |
1+25=26 |
75 |
60 |
1+160 |
|
8-cell |
40 |
128 |
96 |
264 |
1+32 |
112 |
96 |
1+240 |
1+72=73 |
240 |
192 |
1+504 |
|
16-cell |
40 |
120 |
96 |
256 |
1+24 |
80 |
72 |
1+176 |
1+64=65 |
200 |
168 |
1+432 |
|
24-cell |
120 |
384 |
288 |
792 |
1+96 |
312 |
288 |
1+696 |
1+216=217 |
696 |
576 |
1+1488 |
|
120-cell |
1320 |
4800 |
3600 |
9720 |
1+1200 |
4200 |
3600 |
1+9000 |
1+2520=2521 |
9000 |
7200 |
1+18720 |
|
600-cell |
1320 |
4320 |
3600 |
9240 |
1+720 |
2280 |
2160 |
1+5160 |
1+2040=2041 |
6600 |
5760 |
1+14400 |
Yod composition of the faces and
interiors of the 6 polychorons.
(C/C′ = number of external/internal corners; H/H′ = number of external/internal hexagonal yods; B/B′ = number of external/internal boundary
yods;
Y/Y′ = number of external/internal yods; c/h/b/y = total number of corners/hexagonal yods/boundary
yods/yods).
|
Polychoron |
Faces |
Interior |
Total |
|||||||||
|
|
C |
H |
B |
Y |
C′ |
H′ |
B′ |
Y′ |
c |
h |
b |
y |
|
5-cell |
15 |
110 |
95 |
125 |
1+10 |
100 |
1+80 |
1+110 |
1+25=26 |
210 |
1+175 |
1+235 |
|
8-cell |
40 |
352 |
296 |
392 |
1+32 |
320 |
1+256 |
1+352 |
1+72=73 |
672 |
1+552 |
1+744 |
|
16-cell |
40 |
336 |
280 |
376 |
1+24 |
232 |
1+184 |
1+256 |
1+64=65 |
568 |
1+464 |
1+632 |
|
24-cell |
120 |
1056 |
888 |
1176 |
1+96 |
912 |
1+720 |
1+1008 |
1+216=217 |
1968 |
1+1608 |
1+2184 |
|
120-cell |
1320 |
13200 |
10920 |
14520 |
1+1200 |
12000 |
1+9600 |
1+13200 |
1+2520=2521 |
25200 |
1+20520 |
1+27720 |
|
600-cell |
1320 |
12240 |
9960 |
13560 |
1+720 |
6720 |
1+5280 |
1+7440 |
1+2040=2041 |
18960 |
1+15240 |
1+21000 |
(“1” denotes the centre of the
polychoron).
General comments on these tables can be found at the page linked to above. Here, we will confine our remarks to the 16-cell.
 |
 |
|
|
|
1) Its 32 triangular faces contain 256 geometrical elements, where 256 = 44, showing how the Tetrad expresses its geometrical composition. The 16-cell has 168 triangles with 65 corners, where 65 is the number of ADONAI, the Godname of Malkuth, and 168 is the number of Cholem Yesodoth, the Mundane Chakra of this Sephirah. Eight geometrical elements are vertices, so that (256−8=248) more geometrical elements are needed to shape the 16-cell, where 248 is the number value of Raziel, the Archangel of Chokmah. We discover that the 16-cell embodies the dimension 248 of E8.
2) As the 4-d counterpart of the octahedron, the 16-cell comprises 80 vertices, edges, triangular faces & tetrahedral cells, where 80 is the number of Yesod. The 8-cell also has this property, being its dual.
3) 280 yods line the 96 tetractyses in its faces. This is a remarkable, chance-defying conjunction in the same polychoron of the numbers of the Godname (65), Archangel (280) & Mundane Chakra (168) of the same Sephirah (Malkuth). It is a strong signal that the 16-cell plays a central role in the superstring physics of the universe, as has already been indicated earlier by being the atom-like building block of the 8-cell, the 24-cell and the 600-cell within the 421 polytope. See Article 66 for an analysis of the holistic properties of the 16-cell.
4) 64 (=43) corners surround its centre, where 64 is the number value of Nogah, the Mundane Chakra of Netzach.
5) Its 32 triangular faces contain 336 hexagonal yods. This is a basic structural parameter of the E8×E8′ heterotic superstring constituent of atomic nuclei, being the number of circularly polarised oscillations in one revolution of each whorl of the UPA. It confirms the suggestion raised in comment 3 by the appearance in its geometrical and yod composition of three of the four gematria number values associated with Malkuth.
As the 600-cell is the compound of 15 disjoint 16-cells, none of which share any hexagonal yods, there are (15×336=5040=7!) hexagonal yods shaping the 480 faces that make up these 16-cells. This is the number of turns in the outer or inner half of the shadow matter particle. As the E8 Coxeter plane projection of the 240 vertices of the 421 polytope is a compound of two 600-cells, there are as many 16-cells in each 600-cell as there are revolutions of whorls in each half of the shadow matter particle, and there are as many hexagonal yods in the faces of these 16-cells as there are turns in these 15 revolutions. Moreover, given that previous work indicated that an E8′ gauge charge is spread along 42 turns, the 5040 hexagonal yods correspond to (5040/42=120) E8′ gauge charges, which is to what the 120 vertices of each 600-cell correspond (strictly speaking, it would be more accurate to say that they correspond to the roots of E8′). It would therefore seem reasonable to infer that this is not the result of coincidence but that the 336 hexagonal yods in the faces of a 16-cell symbolise the 336 turns in a whorl of the shadow matter particle over which are spread eight E8′ gauge charges denoted by the eight vertices of each of the 30 16-cells in the two 600-cells. This is expressed by the factorisation of the 240 gauge charges: 240 = 30×8, so that, as each E8′ gauge charge is spread over 336 turns, 240×42 = 30×8×42 = 30×336 = 10080, which is the number of hexagonal yods in the 30 disjoint 16-cells in the compound of two 600-cells. The larger and the smaller 600-cells determine the outer and inner halves of the E8-singlet state of the E8×E8′ heterotic superstring. The 3-dimensional, oscillatory form of this shadow matter particle is the physical manifestation of all the hexagonal yods shaping these 16-cells when constructed from Type A triangles. As they symbolise the seven Sephiroth of Construction, this establishes the mathematical connection between the latter and the shadow matter particle. In the case of the UPA, each of the seven so-called "minor whorls" expresses one of the seven Sephiroth of Construction, with the three "major whorls" expressing the Supernal Triad (the three-fold Godhead). The author asked Ronald Cowen whether he noticed any differences between the five whorls that he had counted in the object that was subsequently identified as the basic particle of shadow matter. He replied that, although the particle was more oblate than the UPA, he detected no thickening of any of its whorls relative to the others that was similar to that of the major whorls of the UPA.
In terms of the analogy between the 15 16-cells in each 600-cell (each with 336 hexagonal yods in their Type A faces) and the 15 revolutions (each with 336 turns) of the five whorls making up the outer and inner halves of the shadow matter superstring, the following correspondences exist:
| 8 vertices of 16-cell | ↔ | 8 E8′ gauge charges in one revolution of a whorl; |
| 24 vertices of 24-cell as compound of 3 disjoint 16-cells | ↔ | 24 E8′ gauge charges in 3 outer/inner revolutions of a whorl; |
| (3×336=1008) hexagonal yods in 96 faces of 3 disjoint 16-cells | ↔ | 1008 turns in 3 outer/inner revolutions of a whorl; |
| 120 vertices of 5 disjoint 24-cells in 600-cell | ↔ | 120 E8′ gauge charges in 15 outer revolutions of 5 whorls; |
| 120 vertices of 5 disjoint 24-cells in smaller 600-cell | ↔ | 120 E8′ gauge charges in 15 inner revolutions of 5 whorls; |
| 336 hexagonal yods in Type A faces of 16-cell | ↔ | 336 turns in one revolution of a whorl; |
| (15+15=30) 16-cells in two 600-cells | ↔ | 30 revolutions of 5 whorls; |
| 5040 hexagonal yods in faces of 15 16-cells in 600-cell | ↔ | 5040 turns in 15 revolutions of outer/inner half of 5 whorls; |
| (5040+5040=10080) hexagonal yods in 30 16-cells in two 600-cells | ↔ | 10080 turns in 30 revolutions of 5 whorls. |
These correspondences are too numerous and detailed to be dismissed as the product of chance. Neither Ron Cowen nor the author could have concocted features of the shadow matter particle that would have been necessary for these analogies to emerge. Cowen did not have a knowledge of mathematics or theoretical physics that was advanced enough to allow him to fabricate details consistent with the group theory of E8 and the mathematics of the various polychorons making up the 421 polytope, whilst the author could not have influenced his observations by meeting or corresponding with him (Cowen lived in Canada and the author lived in England) because Cowen made them in 1994 unprompted by the author, recording them in a private meditation report, which the author learnt about only years later when he began to read various drafts of Cowen's manuscript of his book that discussed his earlier clairvoyant observations. These details were therefore already a fait accompli by the time the author first read about them. For this reason, he could not — directly or indirectly — have influenced Cowen as to how he should describe the particle of shadow matter.
Sacred geometries are not a replacement for the search for a "theory of everything." Rather, they complement it. They tell you what to expect to find in such a theory when it is discovered. Their isomorphism guarantees that the theory must exist, for — if archetypal ideas did not exist that become realised in Nature — this vital quality of isomorphism would be absent from sacred geometries, which would no longer be sacred except in the broad, cultural sense of this word. They would not embody the same patterns and the same parameters, which turn out to quantify the structure of basic particles and the forces that operate between them in a way that is consistent with E8×E8′ heterotic superstring theory. Sacred geometry is really sacred arithmetic in disguise. It represents holistic patterns in space whose form and symmetry express powerful numbers and their factorisations. It is therefore not mere coincidence that each half of the basic particle of shadow matter should consist of
1×2×3×4×5×6×7
circularly polarised oscillations (6×7 (=42) per E8′ gauge charge) that express
1×2×3×4×5
gauge charges of E8′ spread over 5 half-whorls that originate in the
1×2×3×4
vertices of each of 5 24-cells in a 600-cell and which are spread over 3 revolutions of each half-whorl as 1×2×4 E8′ gauge charges per revolution, that is, 4 E8′ gauge charges per half-revolution.
| << Previous 1... 8 9 [10] 11 12 ...24 Next >> |