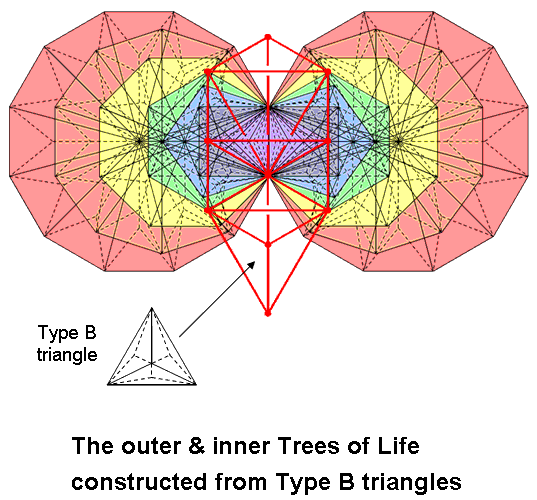
| << Previous 1... 17 18 [19] 20 21 ...39 Next >> |
#19 Properties of the combined outer & inner Trees of Life

Outer Tree of Life
It consists of 16 triangles with 10 corners and 22 sides. Their conversion to Type A triangles (triangles divided into their three sectors) adds 16 corners and (3×16=48) sides, so that there are, upon this conversion, 48 triangles with (10+16=26) corners and (22+48=70) sides, i.e., 144 geometrical elements. Conversion of the original triangles into Type B triangles, i.e., changing the 48 new triangles into Type A triangles, adds 48 corners and (3×48=144) sides, so that there are now 144 triangles with (26+48=74) corners and (70+144=214) sides, i.e., 432 geometrical elements. They include (74+214=288) corners & sides, where 288 = 11 + 22 + 33 + 44. Notice that the construction of the outer Tree of Life from Type B triangles generates (74−10=64=43) corners and (214−22=192) sides, i.e, (64+192=256=44) new corners & sides. Here we see in a simple but remarkable way how the Pythagorean Tetrad expresses the new properties of the sacred geometry of the Tree of Life when it undergoes higher-order transformations.
Inner Tree of Life
The geometrical composition of the (7+7) enfolded Type B polygons is analyzed in #44 at Wonders of correspondences. Their numbers of corners, sides & triangles are tabulated below:
| Corners | Sides | Triangles | Total | |
| 7 enfolded polygons | 88 | 229 | 141 | 458 |
| (7+7) enfolded polygons | 174 | 457 | 282 | 913 |
ELOHIM, the Godname of Binah with number value 50, prescribes the 229 sides of the 141 triangles in the seven enfolded Type B polygons because 229 is the 50th prime number.
Separate outer & inner Trees of Life
Separately, the outer & inner Trees of Life have (74+174=248) corners, (214+457=671) sides
& (144+282=426) triangles, where 248 is the number value of
Raziel, the Archangel of Binah, and the dimension of the superstring gauge symmetry group E8.
Each corner corresponds to a root of E8. Its eight simple roots correspond to the six corners coinciding
with the locations of Sephiroth on the two side pillars and to the two corners that coincide with Tiphareth and
Daath. Its 240 roots correspond to the 240 remaining corners. The six corners are shared with the inner Tree of
Life, leaving (174−6=168) corners of the 282 triangles in the inner Tree
that are unshared with the outer Tree. The two corners are intrinsic to the outer Tree but project onto the
positions of the two endpoints of the root edge. Apart from the six corners, they are the only corners of triangles
in the outer Tree that project onto corners of polygons making up the inner Tree. They leave
(74−2=72) corners of the 144 triangles making up the outer Tree that are intrinsic to it. The
72:168 division of the 240 corners is characteristic of this holistic
parameter (see The holistic pattern). Its counterpart in the
root composition of E8 is the 72 roots of E6, the rank-6,
exceptional group of the symmetry group E8, and the remaining 168 roots of the
latter (see here). In other words, the distinction between the outer and inner Trees of Life
manifests in the subgroups of E8 as the difference between the symmetries of
E6 and the remaining symmetries of E8.
Combined outer & inner Trees of Life
When they are superimposed, the six Sephiroth on the side pillars coincide with the top and bottom corners of the two hexagons and their centres, whilst the two Paths on each side pillar coincide with internal sides of their sectors. No triangles are shared between the outer and inner Trees. To avoid double counting, these 10 shared geometrical elements must be subtracted when ascertaining the geometrical composition of the combined Trees of Life. In this case, they have 426 triangles with (248−6=242) corners and (671−2−2=667) sides, i.e., 1335 geometrical elements. There are 240 corners other than the endpoints of the root edge.
The combined Trees have (242+426=668) corners & triangles (666 outside the root edge) and 667 sides (666 outside the root edge). There are (668−2−6=660) corners & triangles other than the two endpoints of the root edge and the six corners that are shared between the outer & inner Trees. 660 = 66×10, where 66 is the 65th integer after 1. This shows how ADONAI, the Godname of Malkuth with number value 65, prescribes the outer and inner forms of the Tree of Life.
The number of corners, sides & triangles in the combined Trees = 242 + 667 + 426 = 1335. The number of corners & sides = 242 + 667 = 909. The number of corners & sides outside the root edge that do not include shared, Sephirothic points = 909 − 3 − 6 = 900 = 90×10. The number 90 is a holistic parameter, being the sum of the 10 integers making up the Lambda Tetractys (see here and here). As the table indicates that the (7+7) enfolded polygons have 913 corners, sides & triangles, of which three corners and sides make up the root edge and 10 corners & sides are shared with the outer Tree, the inner Tree of Life has 900 intrinsic corners, sides & triangles outside the root edge. This is discussed in detail here.
The number of sides & triangles in the (7+7) enfolded polygons = 457 + 282 = 739. There are 369 sides & triangles on either side of the root edge. This is the sum of the number values of the Godnames of the first seven Sephiroth:
21 + 26 + 50 + 31 + 36 + 76 + 129 = 369.
Yod composition of the outer & inner Trees of Life
When the 282 triangles of the inner Tree of Life with Type B polygons are tetractyses, they contain 1370 yods (see #3). Each of the 16 primary triangles in the outer Tree of Life has 37 yods inside it when it is a Type B triangle. Each of their 22 sides has two hexagonal yods. The number of yods in the outer Tree of Life when its 16 triangles are Type B = 10 + 22×2 + 16×37 = 646. Starting with the 10 corners of these triangles, its conversion into Type B triangles generates (646−10=636) yods, where 636 is the number value of Rashith ha Gilgalim, the Mundane Chakra of Kether. Separately, the outer & inner Trees of Life have (646+1370=2016) yods. Seven yods are on each side pillar and are shared with the inner Tree of Life because they lie on sides of tetractyses in each hexagon. So are the two hexagonal yods on the Chesed-Geburah Path, which are the centres of the two enfolded triangles. Hence, these have to be subtracted when the Trees are combined in order to avoid double-counting. The number of yods in the pair of superimposed Trees = 2016 − 7 − 7 − 2 = 2000. 630 yods belong to the outer Tree and 1370 yods belong to its inner form, where 630 is the number value of Seraphim, the Order of Angels assigned to Geburah. The 14 polygons of the inner Tree has 68 corners outside its root edge, six of which are shared with its outer form. Hence, (68−6=62) corners outside the root edge are intrinsic to the inner Tree (31 for each set of seven polygons), where 31 is the number value of EL, the Godname of Chesed and 62 is the number value of Tzadkiel, the Archangel of Chesed. Of these, the outermost corners of the two pentagons coincide with the centres of the decagons. Hence, 60 intrinsic corners outside the root edge are pure corners. The number of yods in the combined outer & inner Trees of Life other than such corners = 2000 − 60 = 1940 = 194×10, where 194 is the number value of Tzadekh, the Mundane Chakra of Chesed. Here is a remarkable instance of three numbers appearing naturally in the same context that refer to the same Sephirah!
Of the 646 yods in the outer Tree of Life with 16 Type B triangles, 10 yods are at their Sephirothic corners and 16 yods are at their centres. There are (646−10−16=620) yods in the outer Tree of Life other than corners and centres of its triangles. 620 is the number value of Kether. The polygonal counterpart of this property is the set of 620 hexagonal yods making up the decagon with 2nd-order tetractyses as its sectors (see #5). See also #22, which proves that the combined outer & inner Trees of Life have 620 hexagonal yods outside the root edge when their triangles and polygons are Type A.
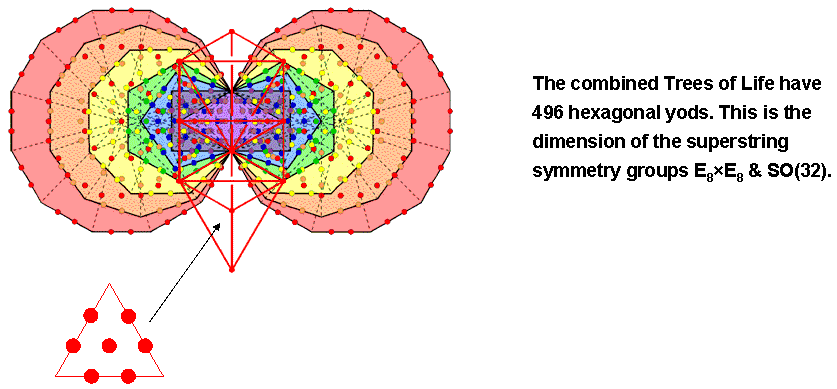
The number of yods lining the 144 tetractyses in the 16 Type B triangles of the outer Tree of Life = 646 − 144 = 502. Six of these located at the positions of Sephiroth are shared with the (7+7) enfolded polygons. Hence, there are (502−6=496) yods on sides of tetractyses that are not Sephirothic points shared with the inner Tree of Life. This is how the outer Tree of Life embodies the number value 496 of Malkuth and the dimension of E8×E8 & SO(32), the two symmetry groups describing the forces between heterotic superstrings (see here).
The number of yods lining the 282 tetractyses of the inner Tree of Life = 1370 − 282 = 1088. (502+1088=1590) yods line tetractyses in the separate outer and inner Trees of Life. The number of yods on sides of the (144+282=426) tetractyses in the combined pair of Trees = 1590 − 7 − 7 − 2 = 1574. The number of such yods that are not shared = 1574 − 16 = 1558. They comprise the centres of the two sets of four polygons in the inner Tree if Life that do not coincide with corners (remember that the outermost corner of the pentagon is the centre of the decagon) and 1550 (=155×10) other yods surrounding them. This shows how ADONAI MELEKH, the Godname of Malkuth with number value 155, prescribes how many yods are needed to shape all the sectors of triangles making up the outer and inner forms of the Tree of Life (see also #21).
(22×2 + 10 = 54) yods line the 22 sides of the 16 triangles in the outer Tree of Life. Of these, four hexagonal yods and three Sephirothic corners on each side pillar coincide with yods on sides of polygons in the inner Tree of Life when it is superposed onto the plane containing the pillars. This leaves 40 yods lining sides of triangles in the outer Tree that do not coincide with the 236 yods lining sides of polygons. The number of yods lining triangles and polygons in the combined Trees = 40 + 236 = 276. Therefore, 272 yods outside the root edge line sides of triangles and polygons. This is the number value of Cherubim, the Order of Angels assigned to Yesod. They comprise 72 corners and 200 hexagonal yods, where 72 is the number value of Chesed.
Hexagonal yod composition of outer & inner Trees of Life
Firstly, consider the simplest case where the triangles of the outer Tree of Life are tetractyses and the polygons in its inner form are Type A. The former has 70 yods, of which 60 are hexagonal (see here). The latter has 524 yods (see here), of which 80 are corners of sectors (see here) and 444 are hexagonal (see here). There are eight hexagonal yods on the four sides of the sectors of the two hexagons that are shared with the outer Tree of Life because they lie on its side pillars. Although the two hexagonal yods on the Chesed-Geburah Path are also the centres of the two enfolded triangles, they still count as hexagonal yods in determining the hexagonal yod population of the combined Trees of Life. The number of hexagonal yods in the combined Trees = 60 + 444 − 8 = 496. This is both the number value of Malkuth and the dimension of E8×E8 & SO(32) — the two symmetry groups that allow interactions between superstrings that are free of quantum anomalies (see discussion here under the heading "Superstring gauge symmetry group"). What more explicit proof could there be that the Tree of Life encodes superstring theory — or, rather, M-theory, the 'theory of everything' that contains the five versions of superstrings as approximations?
The outer Tree of Life has 16 hexagonal yods at the centres of its 16 tetractyses and the inner Tree has 94 hexagonal yods at the centres of its 94 tetractyses. The number of hexagonal yods lining sides of the (16+94=110) tetractyses in the combined Trees = 496 − 110 = 386. Outside the root edge of the (7+7) enfolded polygons are 384 hexagonal yods lining 192 sides of 110 tetractyses. This number is a parameter of holistic systems (see here), e.g., the 64 hexagrams used in the ancient Chinese I Ching system of divination have 384 lines & broken lines (see here).
The 94 tetractyses in the inner Tree of Life have 80 corners and the 16 tetractyses in the outer Tree of Life have four corners that are unshared with the former. The 110 tetractyses in the combined Trees have (80+4=84) corners, where
84 = 12 + 32 + 52 + 72.
As we have just seen, 386 hexagonal yods line their sides. Therefore, (84+386=470=47×10) yods line their sides, where 47 is the 15th prime number. This shows how YAH, the Godname of Chokmah with number value 15, prescribes the combined Trees of Life.
Next, let us consider the case where both the triangles of the outer Tree of Life and the polygons of the inner Tree of Life are Type A. Inside each of the 16 triangles of the former are nine hexagonal yods. The number of hexagonal yods in the outer Tree = 22×2 + 16×9 = 44 + 144 = 188. The inner Tree of Life has 444 hexagonal yods, of which eight are shared with its outer form. The number of hexagonal yods in the combined Trees of Life = 188 + 444 − 8 = 624. As found in #1, this is the number of hexagonal yods in the seven separate Type B polygons. The 16 triangles in the outer Tree have (10+16=26) corners of 48 tetractyses and the 94 tetractyses in its inner form have 80 corners, of which six are shared as such and two (centres of the two triangles) coincide with hexagonal yods on the Chesed-Geburah Path. Combined, the two Trees of Life have (26+80−6−2=98) corners. Therefore, they have (624+98=722) yods, i.e., 718 yods other than the four yods in the root edge. Of these, 68 are corners of the (7+7) enfolded polygons. This leaves (718−68=650=65×10) yods outside the root edge that are not corners of polygons. This shows how ADONAI, the Godname of Malkuth with number value 65, prescribes the form of the combined Trees of Life. We saw in #17 that ADONAI also prescribes the 650 yods associated with each set of seven enfolded Type B polygons that are not their corners. In each case, this number is the extra number of yods needed to construct the Trees, given their Sephirothic points and/or polygonal corners.
The 48 tetractyses in the outer Tree of Life with Type A triangles have 48 hexagonal yods at their centres. The 94 tetractyses in the inner Tree with Type A polygons have 94 hexagonal yods at their centres. The number of hexagonal yods on the sides of the (48+94=142) tetractyses in the combined Trees of Life = 624 − 142 = 482. Eight of these are shared by both Trees, leaving (482−8=474) unshared hexagonal yods that line sides of tetractyses. 474 is the number value of Daath ("knowledge"), the non-Sephirah.
As calculated above, the combined Trees of Life have 722 yods. With respect to the two sets of the seven separate Type B polygons separated by the root edge, this is the sum of the two yods in the latter associated with each set of polygons and the 720 yods surrounding their centres (see here). The linked page also discusses how this parameter of holistic systems appears in the five Platonic solids, the decagon & the disdyakis triacontahedron (see also #6).
Finally, let us consider the case where the triangles in the outer Tree of Life and the polygons of the inner Tree of Life are Type B (the case that was considered initially in the context of their geometrical compositions). Inside each Type B triangle are 33 hexagonal yods. The number of hexagonal yods in the outer Tree of Life = 22×2 + 16×33 = 572. The 282 tetractyses in the (7+7) enfolded polygons have 174 corners and 1370 yods. Therefore, they have (1370−174=1196) hexagonal yods. Eight of these are shared with the outer Tree of Life. The number of hexagonal yods in the combined Trees of Life = 572 + 1196 − 8 = 1760. We found in #26 at Superstrings as sacred geometry/Tree of Life that the seven enfolded Type A polygons have 176 hexagonal yods. This means that the 70 Type A polygons enfolded in 10 overlapping Trees of Life on each side of the central Pillar of Equilibrium have 1760 hexagonal yods. Embodied in the unified geometry of its outer and inner forms, the Tree of Life has as many hexagonal yods as its inner form has in 10 Trees of Life! This is remarkable, for its demonstrates how a single Tree of Life encodes its potential 10-fold development through a different order of transformation of its geometry. There are eight hexagonal yods shared by the two Trees of Life and two hexagonal yods in the root edge. Hence, (1760−8−2=1750=175×10) hexagonal yods are outside the root edge that are unshared. What emerges here is a division that is analogous to the 175/176 distinction in the augmentation of major and minor whorls of the UPA (see here). The number 175 determines unshared yods and the difference 1 between 175 and 176 determines either shared hexagonal yods or hexagonal yods in the root edge. This quality of being shared by both the outer & inner forms of the Tree of Life is characteristic of this difference when it manifests in other contexts, e.g., the first (6+6) enfolded polygons constitute a holistic subset of the (7+7) polygons and the first six polygons enfolded in seven overlapping Trees have 176 corners, of which 175 are intrinsic to the 42 polygons and one (the topmost corner of the hexagon enfolded in the seventh Tree) is shared with the hexagon enfolded in the eighth Tree because it coincides with its lowest corner. The fact that the seven Trees bear a formal correspondence to the seven Sephiroth of Construction when the ten Sephiroth of the Tree of Life are each replaced by Trees is further indication that the number 176 is a parameter of holistic systems.
The 1750 hexagonal yods outside the root edge unshared by both the outer and inner forms of the Tree of Life have a remarkable parallel in the dodecahedron, as explained in the next page.
| << Previous 1... 17 18 [19] 20 21 ...39 Next >> |