| << Previous 1... 16 17 [18] 19 20 ...39 Next >> |
#18 EL CHAI prescribes the inner Tree of Life

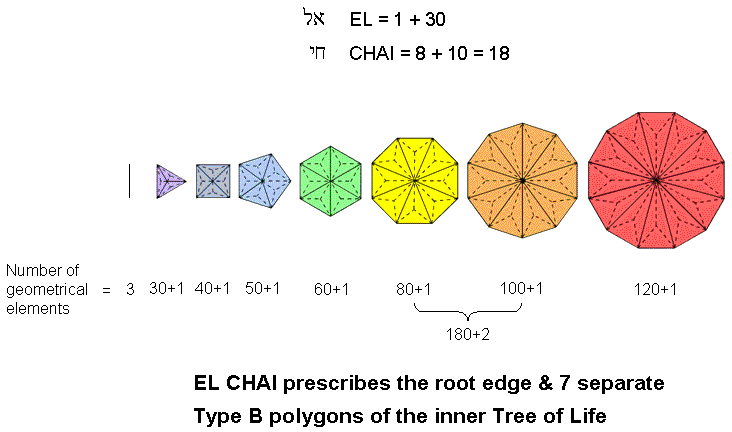
A Type B polygon has (2n+1) corners and 5n sides of 3n triangular sectors, i.e., (10n+1) geometrical elements. Of these, 5n corners & sides and 5n triangles surround its centre. The centres of the seven separate Type B polygons of the inner Tree of Life with 48 corners are surrounded by (5×48=240) corners & triangles and 240 sides, i.e., 480 geometrical elements. This shows how the inner Tree of Life embodies the division
480 = 240 + 240
that is characteristic of holistic systems. Its counterpart in superstring theory are the (240+240=480) roots of E8×E8, one of the two gauge symmetry groups of the heterotic superstring (see here in the section entitled "Superstring gauge symmetry group").
Tabulated below are the geometrical elements in the root edge and the seven separate Type B polygons:
Geometrical composition of the root edge & the seven Type B polygons.
|
Root edge |
Triangle |
Square |
Pentagon |
Hexagon |
Octagon |
Decagon |
Dodecagon |
Total |
|
|
Corners |
2 | 6+1 | 8+1 | 10+1 | 12+1 | 16+1 | 20+1 | 24+1 | 96+9 |
| Sides (5n) |
1 | 15 | 20 | 25 | 30 | 40 | 50 | 60 | 240+1 |
| Triangles (3n) |
0 | 9 | 12 | 15 | 18 | 24 | 30 | 36 | 144 |
| Total | 3 | 30+1 | 40+1 | 50+1 | 60+1 | 80+1 | 100+1 | 120+1 | 480+10 = 490 |
The seven Type B polygons have (96+240=336) corners & sides surrounding their centres. They embody the
superstring structural parameter 336, namely, the 336 circular turns in one revolution of each whorl of the
UPA/subquark superstring.
Together with the root edge (a single straight line), the seven separate polygons have 490
(=49×10) corners, sides & triangles. They are prescribed by EL ChAI, the Godname of Yesod,
which has number value 49. That this is not coincidence is indicated by the following: the octagon
and decagon have 180 (=18×10) geometrical elements surrounding their centres, where 18 is the number value of CHAI
(ChI), the value 8 of the Hebrew letter chet corresponding to the octagon with 80 (=8×10)
geometrical elements around its centre and the value 10 of the letter yod corresponding to the decagon with 100
(=10×10) geometrical elements around its centre, whilst the remaining polygons & root edge have 310
(=31×10) geometrical elements made up of 300 (=30×10) elements surrounding the centres and 10
(=1×10) elements that are either centres or belong to the root edge. This reproduces the letter values of EL:
31 = 1 + 30.
The seven Type B polygons have 384 sides & triangles made up of the 48 sides & triangles in the hexagon and 336 sides & triangles in the remaining polygons. This 48:336 division of the number 384 is characteristic of holistic systems (see here). The triangle, octagon & decagon have 168 sides & triangles, as have the square, pentagon & dodecagon (these subsets of polygons are the only ones with this number of sides & triangles). The seven polygons, therefore, display the 168:168 division of the number 336 that is also characteristic of these systems, having its physical manifestation in the subquark state of the E8×E8 heterotic superstring paranormally observed by Besant & Leadbeater as the 168 circularly polarized oscillations in a half-revolution of each whorl. This division also appears in the 336 corners & sides that surround the centres of the seven polygons because the triangle, pentagon, hexagon & decagon have 168 corners & sides, as do the square, octagon & dodecagon (these polygons are the only ones that have 168 corners & sides).
| << Previous 1... 16 17 [18] 19 20 ...39 Next >> |