#50 The 3:69:168 pattern in seven sacred geometries

1-tree
The 1-tree (lowest Tree of Life) with its 19 triangles turned into tetractyses has 80 yods. Eleven of these are SLs, leaving 69 black yods. When its triangles are Type A triangles, the 1-tree has 251 yods in (19×3=57) tetractyses. (251−11=240) of these are not SLs. They comprise the original 69 black yods and 171 new yods. Three of the latter indicated by green yods are aligned with the Daath-Tiphareth Path, whose projection onto the plane of the (7+7) polygons of the inner Tree of Life is their root edge. Two pairs of red and black yods aligned with this Path project onto the pair of hexagonal yods in the root edge, but the three green yods do not project onto any yod. This leaves 168 red yods inside the 19 Type A triangles.

2-d Sri Yantra
At the centre of the 2-dimensional Sri Yantra is a point, or bindu, that symbolizes the Absolute, the source of all existence. It is bounded by the three green sides of a triangle, although, strictly speaking, this does not count as a triangular area because of the embedding in its plane of the bindu as an object that is separate and distinct from it, even though it is only a mathematical point. The bindu symbolizes Brahman (the Absolute), whilst the triangle denotes the trimûrti, or trinity, of Brahma (creator), Vishnu   

The trimûrti of the three Hindu Gods: Brahmā, Vishnu, and Shiva (left to right) at Ellora Caves, near Aurangabad, in India. They are expressed in sacred geometries
by the three generic, structural components that are their seed or source elements, namely, the "3" in the 3:69:168 pattern that is common to these geometries.

(preserver or maintainer) and Shiva (the destroyer or transformer). They are surrounded by 42 red triangles with 68 black corners and 126 red sides. Including the lowest corner of the central triangle, there are 69 black points, three green lines and (42+126=168) red lines & triangles in the 240 geometrical elements that surround the centre of the Sri Yantra.

Two separate sets of 7 enfolded polygons
120 yods line the sides of the seven enfolded polygons of the inner Tree of Life. They comprise 36 corners and 84 red hexagonal yods. The 240 yods on the boundaries of both sets of seven polygons consist of 72 corners and 168 red hexagonal yods. Of the former, three green corners are the corners of the triangle in one set. Hence, the three corners of the simplest regular polygon, namely, the equilateral triangle, 69 black corners of the 13 other polygons and 168 red hexagonal yods lie on the boundaries of the 14 polygons.

Two separate Type B dodecagons
Divided into their sectors, the two Type A dodecagons have 72 corners, sides & triangles surrounding their centres. A corner of the polygon, an outer side and an interior side (coloured green in the diagram above) are the three types of geometrical elements that generate its sectors. Hence, they are each repeated 23 times in the 69 extra black corners & sides needed to construct the dodecagons. Changed into two Type B dodecagons, their centres are surrounded by 240 geometrical elements. 168 red corners, sides & triangles are added by this transformation.

Disdyakis triacontahedron
The disdyakis triacontahedron has 62 vertices, 60 of which surround an axis passing through two opposite vertices. The vertices are of three types: A, B (vertices of an icosahedron) & C (vertices of a dodecahedron). Three such vertices are shown above as green. 57 vertices in addition to these surround the axis. The polyhedron has 180 edges. When the axis passes through two A vertices, 12 of these edges are sides (coloured red) of the central polygon whose corners are four A vertices, four B vertices and four C vertices. 168 edges extend above and below this polygon, 84 in each half of the polyhedron. The 240 vertices & edges that surround the axis consist of a set of three generic vertices, (57+12=69) vertices or sides of the central 12-gon and 168 edges. This pattern of numbers exists only for an axis passing through two A vertices because only for this type of axis do the vertices in the central plane perpendicular to it form a 12-gon. As for the 3:69:168 pattern in the two Type B dodecagons, in which the number 3 refers to three types of geometrical elements, so it denotes the three types of vertices making up the disdyakis triacontahedron. As with the two dodecagons, it is not essential to specify here the set of three vertices, although — given that the A vertices at the extremities of the polyhedron located on the axis are the starting point and endpoint of its generation — it is natural to choose the uppermost A vertex and a B and a C vertex at the corners of one of the faces of the pyramid with a Golden Rhombic base immediately below it (see the diagram above) because this selection is consistent with the meaning of the number 3 in the 3:69:168 pattern as the source or starting point of the four sacred geometries discussed earlier.

First three Platonic solids
When the 60 sectors of their 18 faces are Type A triangles, the tetrahedron, octahedron & cube have 240 hexagonal yods. The tetrahedron has 48 hexagonal yods that comprise three green hexagonal yods at the centres of the three tetractyses in one face, 21

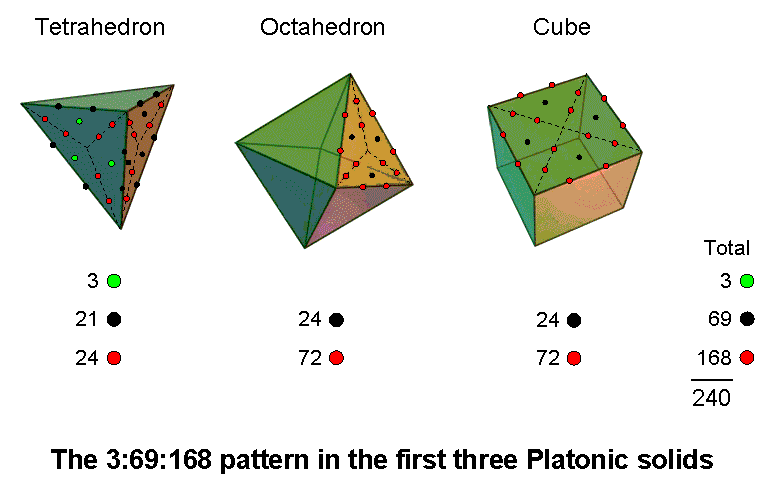
black hexagonal yods that are either on its edges or at the centres of the nine tetractyses in the other three faces and 24 red hexagonal yods on internal sides of the 60 tetractyses. The 24 tetractyses in the eight faces of the octahedron contain 24 black hexagonal yods at their centres and 72 red hexagonal yods on their sides. The 24 tetractyses in the six faces of the cube contain 24 black hexagonal yods at their centres and 72 red hexagonal yods on their sides. There are three green hexagonal yods, 69 black hexagonal yods and 168 red hexagonal yods in the faces of the first three Platonic solids.

The {3,7} tiling of the 3-torus with tetractyses
When their square faces are stuck together, four triangular prisms and six square antiprisms create an object that is topologically equivalent to a 3-torus. Its 56 hyperbolic triangles are the {3,7} tiling on the 3-torus of the 168 automorphisms of the Klein quartic:

X³Y + Y³Z + Z³X = 0

where X, Y & Z are complex variables (see Article 43). Transformed into tetractyses, they contain 248 yods (see the table in the diagram below). They symbolize the 248 roots of the rank-8 Lie group E₈. Eight of these are white yods at the centres of the triangular faces of the triangular prisms (the diagram shows only one for the sake of clarity). The remaining 240 yods comprise 72 yods at either the centres or the corners of the 56 tetractyses and 168 red hexagonal yods on their 84 sides. The yods at the
  

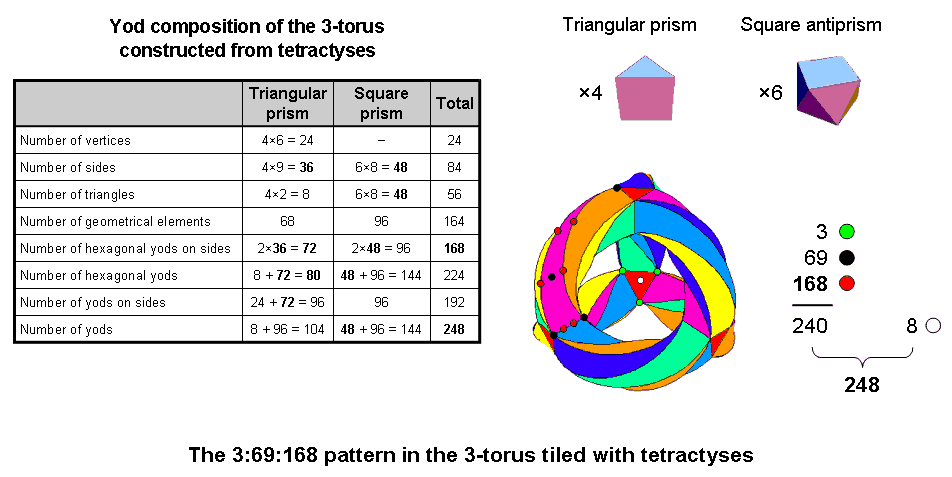
corners of one triangular face are coloured green. The 21 other vertices of the prisms & antiprisms and the centres of the 48 tetractyses in the faces of the antiprisms (i.e., 69 yods), are coloured black. Intuitively speaking, it makes sense to regard the three green corners of one face of one triangular prism as the natural starting point for the construction of the 3-torus from 56 triangles. It is simply like starting with a point, calling it the first vertex of a tetrahedron and then creating the rest of it from this point, only this time we start with a triangle, namely, one of the faces of one of the four triangular prisms, and proceed to stick them to the antiprisms. The conversion into tetractyses of the 56 hyperbolic triangles in the {3,7} tiling of the 3-torus displays the same 3:69:168 pattern as that found in other sacred geometries. This is because the Klein quartic and the 3-torus play a fundamental role in the physics of the E₈×E₈ heterotic superstring, which this website demonstrates conforms to different sacred geometries. The embodiment in the 3-torus of both the numbers 168 and 248 as basic structural and dynamical parameters of the superstring cannot be a coincidence!

According to the table opposite, the 192 yods lining the 56 tetractyses comprise the 24 vertices of the four triangular prisms and 168 red hexagonal yods. This 24:168 division (actually a 3:21:168 division) is characteristic of sacred geometries (see The holistic pattern). Notice also that the 36:48 division of the 84 sides of the triangular prisms & square antiprisms conforms to the pattern of holistic systems. For example, it is found in the 2nd-order tetractys as the 36 yods lining its sides and as the 48 yods inside it that surround its centre, or, alternatively, as the 36 yods either in the three tetractyses at its corners or at corners of the other tetractyses and as the 48 hexagonal yods in the seven other tetractyses that surround its centre (see here).

Here is a clear, remarkable illustration of the correspondence between seven objects that possess sacred geometry. Not only do they contain 240 structural components — yods or geometrical elements — but this number also divides up in a natural way into analogous sets of three, 69 and 168 components. See also here.

 

<< Previous    1...   48  49  [50]  51  52  ...81    Next >>

Home