#48 How various sacred geometries embody the number 252

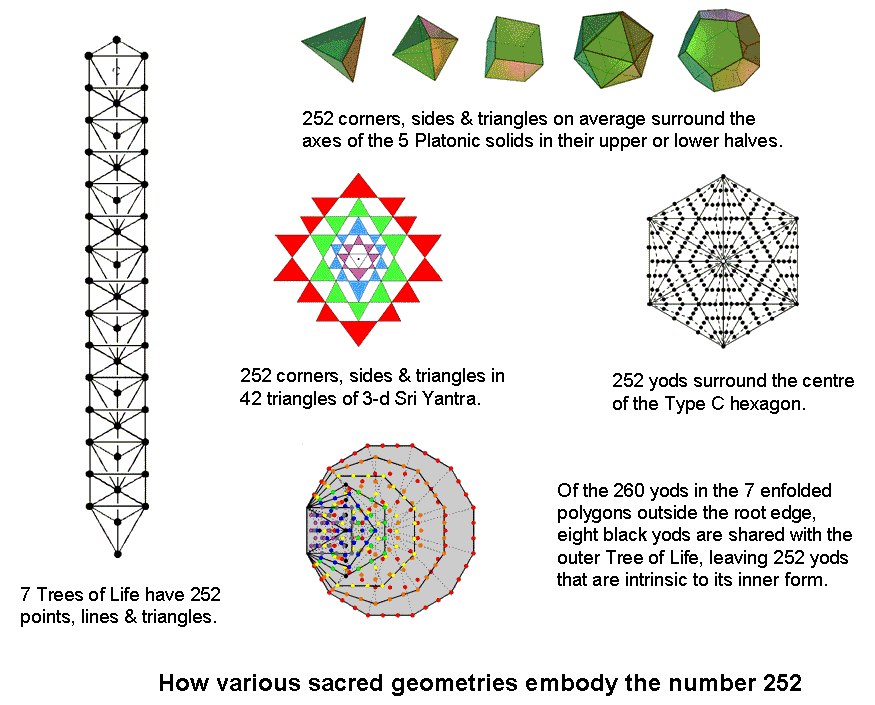
7 overlapping Trees of Life
n overlapping Trees of Life have (12n+4) triangles with (6n+4) corners and (16n+6) sides, i.e., (34n+14) geometrical elements. Seven overlapping Trees are composed of 252 geometrical elements.

5 Platonic solids
As shown in #19 at Wonders of sacred geometry/superstrings, when the vertices and face-centres of the five Platonic solids are joined to their centres, there are on average 252 geometrical elements in each half of the solids that surround their axes.

3-dimensional Sri Yantra
There are 84 corners and 126 sides of the 42 triangles, i.e., 252 geometrical elements, surrounding the central triangle in the 3-dimensional Sri Yantra.

Type C hexagon
The number of yods in the Type C n-gon = 42n + 1, where "1" denotes its centre. The number of yods surrounding the centre of the Type C hexagon (n=6) = 252.

Inner Tree of Life
When the 47 sectors of the seven enfolded polygons of the inner Tree of Life are tetractyses, there are 260 yods outside the root edge. The plane of the polygons contains the two side pillars of the outer Tree of Life. When the 16 triangles in the latter are tetractyses, the black centre of the triangle belonging to the set of enfolded polygons coincides with a hexagonal yod on the Path connecting Chesed and Geburah, this being a side of a triangle with Tiphareth at its other corner. Similarly, the second hexagonal yod on this Path coincides with the centre of the triangle belonging to the other set of enfolded polygons. Also, seven black yods on the two internal, vertical sides of tetractyses in the hexagon coincide with yods on the Pillar of Mercy that belong to tetractyses of the outer Tree of Life, and, similarly, for the corresponding seven black yods in the hexagon belonging to the other set of polygons (not shown). Eight black yods in a set of seven enfolded polygons, therefore, are shared with the outer Tree of Life, leaving 252 yods that are intrinsic to its inner form (likewise for the 252 such yods in the set of seven polygons enfolded on the other side of the middle Pillar of Equilibrium). See also #38.

The eight yods shared with the outer Tree of Life when its triangles are tetractyses are analogous to the eight geometrical elements making up the central bindu point and triangle of the 3-dimensional Sri Yantra (see #9) and to the eight tetrahedra in the seven overlapping Trees of Life (see #8). It is implausible to attribute to chance this 8:252 division displayed in three sacred geometries. Instead, it manifests because they are all representations of the seven Sephiroth of Construction, as most explicitly indicated by the seven Trees of Life, as well as by the Sri Yantra, which maps the seven planes of consciousness (see here), and the seven enfolded polygons, which encode these planes (see here).

3-torus with {3,7} tessellation
As the table in #32 shows, the 3-torus constructed from four triangular prisms and six square antiprisms comprises 56 triangles which, when Type A triangles, have 168 sectors with 252 sides. The 56 hyperbolic triangles in the 3-torus turned inside-out also have 168 sectors with 252 sides.

Disdyakis triacontahedron
According to #26, when we consider the seven polygons formed by vertices of the disdyakis triacontahedron that are perpendicular to an axis passing through two opposite A vertices, there are 248 corners, sides & triangles in each half of the polyhedron that surround the centres of the four types of polygons. Including the A vertex and the centres of the three polygons either above or below the central one, there are 252 geometrical elements in each half of the disdyakis triacontahedron that surround its centre.

According to #31, when the 120 faces of the disdyakis triacontahedron are divided into their sectors and their centres and the vertices are joined to the centre of the polyhedron and the internal triangles divided into their sectors, there are 2520 (=252×10) corners, sides & triangles in each half of the polyhedron that surround an axis passing through two diametrically opposite vertices. This should be compared with the 2520 corners, sides & triangles that surround the axes of the five Platonic solids (see above and here), that is, the 252 geometrical elements on average in each half of a Platonic solid that surround its axis.

The three helical major whorls of the UPA contain (3×1680 = 5040) turns, or so-called "1st-order spirillae." They spiral 2½ times around its spin axis, containing 2520 turns in their outer revolutions, and 2½ times in an inner, narrower spiral, containing another 2520 turns. The five Platonic solids are the analogue of each half of the three major whorls because their axes are surrounded by 2520 geometrical elements. But the disdyakis triacontahedron is the complete analogue because it is the counterpart of both halves of the three major whorls, each half of this polyhedral form of the outer Tree of Life having 2520 geometrical elements that surround its axis.

<< Previous    1...   46  47  [48]  49  50  ...81    Next >>

Home