| << Previous 1... 32 33 [34] 35 36 ...40 Next >> |
#34 The 3:69:168 pattern in sacred geometries

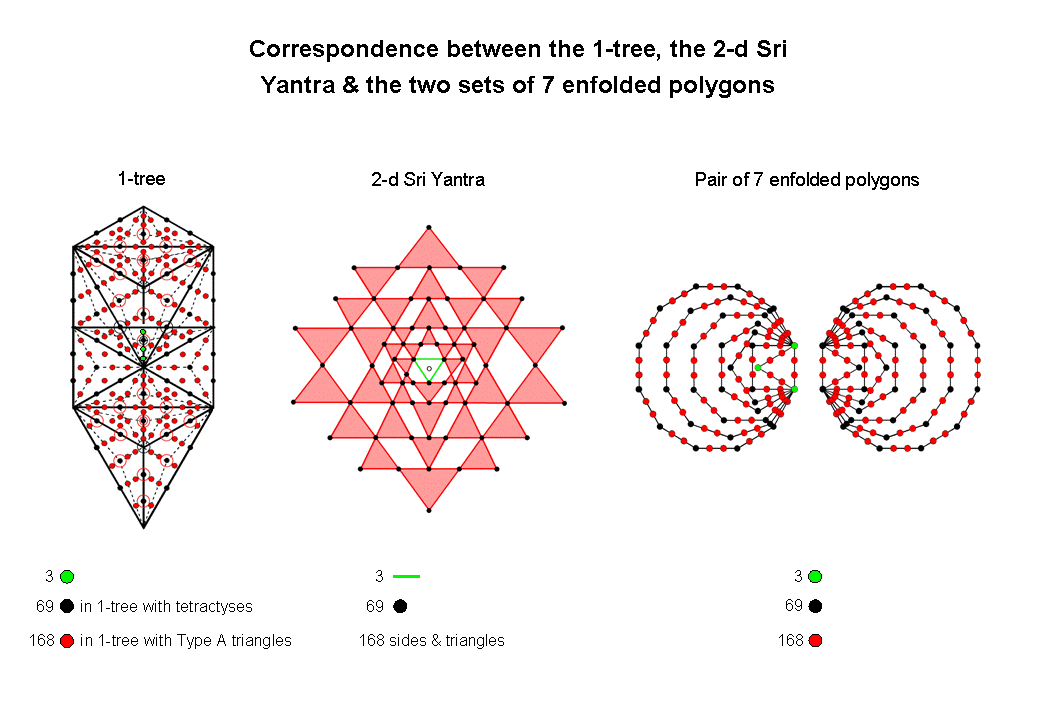
The 1-tree (lowest Tree of Life) with its 19 triangles turned into tetractyses has 80 yods. Eleven of these are SLs (corners of the 19 triangles), leaving 69 black yods. When these triangles are Type A triangles, the 1-tree has 251 yods. 240 of these are not SLs. They comprise the 69 yods and 171 new yods. Three of the latter indicated by green yods are aligned with the Daath-Tiphareth Path whose projection onto the plane containing the two sets of seven enfolded polygons is the root edge. Two pairs of red and black yods become projected onto the pair of hexagonal yods of the root edge. The three green yods project onto the root edge but their projections do not coincide with any yods belonging to the (7+7) enfolded polygons. This leaves 168 red yods in the 1-tree .
The 2-dimensional Sri Yantra consists of a central point, or bindu, that is bounded by three green sides of a triangle, although, strictly speaking, it does not count as a triangular area because of the presence of this mathematical point as an object that is separate and distinct from this triangle. They are surrounded by 42 red triangles with 68 black corners and 126 red sides. Including the lowest corner of the central triangle, there are 69 black points, three green lines and (42+126=168) red lines & triangles surrounding the central bindu of the Sri Yantra (indicated in the diagram by a small circle).
120 yods line the sides of the seven enfolded polygons of the inner Tree of Life. They comprise 36 corners and 84 red hexagonal yods. The 240 yods on the boundaries of both sets of seven polygons consist of 72 corners and 168 red hexagonal yods. Of the former, three green corners are the corners of the triangle in one set. Hence, the three corners of the simplest regular polygon, namely, the equilateral triangle, 69 black corners of the 13 other polygons and 168 red hexagonal yods lie on the boundaries of the 14 polygons.
The 1-tree, 2-dimensional Sri Yantra and the two sets of seven enfolded polygons of the inner Tree of Life display the same 3:69:168 pattern because they are equivalent representations of the same holistic paradigm. They embody the number 240 as a defining parameter of sacred geometries (and holistic systems in general). It is discussed under the heading "240 = 72 + 168" at The holistic pattern.
Divided into their sectors, the two Type A dodecagons have 72 corners, sides & triangles surrounding their centres. A corner of the polygon, an outer side and an interior side (coloured green in the diagram below) are the three classes of geometrical elements that generate its sectors. Hence, they are each repeated 23 times in the 69 extra red corners & sides needed to construct the dodecagons. Changed into two Type B dodecagons, their centres are surrounded by 240 geometrical elements. 168 blue corners, sides & triangles (seven in each of their 24 sectors) are added by this transformation:
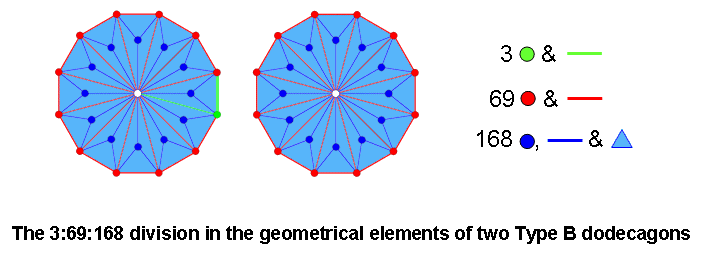
The fact that the 3:69:168 pattern exhibited by the 1-tree, 2-d Sri Yantra and the inner Tree of Life appears also in the two separate Type B dodecagons is yet more confirmation of the status of the latter as the polygonal counterpart of the Tree of Life. The number of corners & sides in the sectors surrounding the centre of a Type A n-gon = 3n. There are 10n corners, sides & triangles surrounding the centre of a Type B n-gon, that is, 7n more geometrical elements. For the dodecagon (n=12), 84 extra elements are added. The 84:84 division of the 168 extra elements needed to convert the two Type A dodecagons into Type B dodecagons is a characteristic feature of holistic systems. It physically manifests in the UPA/subquark state of the E8×E8 heterotic superstring as the 840 circular turns in the inner and outer halves of each whorl. The boundaries of the two dodecagons comprise 24 corners and 24 sides, that is, 48 points & lines. This 24:24 division of the number 48 is also characteristic of holistic systems (see the diagram at the beginning of The holistic system). 48 is the number value of Kokab, the Mundane Chakra of Hod. The fact that each of the 24 sectors of the two Type B dodecagons adds 10 geometrical elements is a clear illustration (discussed in Article 53) of how the 240 structural components of sacred geometries factorize into 10 sets of 24. They manifest in the subquark superstring as its ten whorls, along each of which 24 gauge charges of the gauge symmetry group E8 are spread. How five sacred geometries embody the holistic parameter 240 is analyzed here.
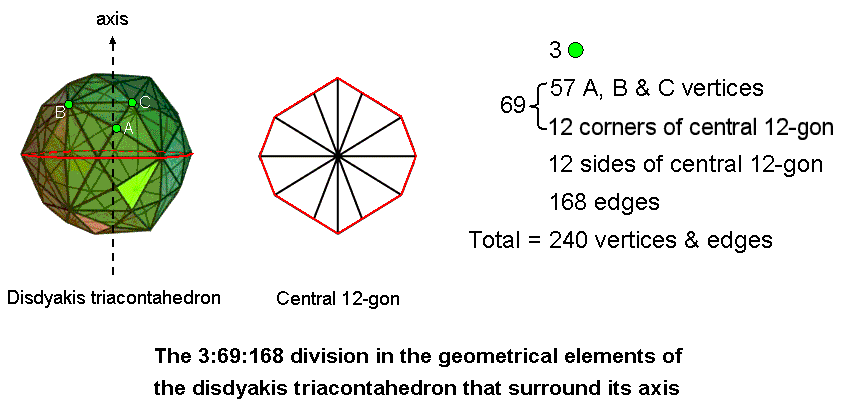
The disdyakis triacontahedron is the Yin aspect of the Polyhedral Tree of Life, its Yang aspect being the so-called "144 Polyhedron" (see here). It has 62 vertices, 60 of which surround an axis passing through two opposite vertices. The vertices are of three types: A, B (vertices of an icosahedron) & C (vertices of a dodecahedron). 57 vertices in addition to these three surround the axis. The polyhedron has 180 edges. When the axis passes through two A vertices, 12 of these edges are sides (coloured red) of the central polygon whose corners are four A vertices, four B vertices and four C vertices. 168 edges extend above and below this polygon, 84 in each half of the polyhedron. The 240 vertices & edges that surround the axis consist of a set of three generic vertices (one of each type coloured green), (57+12=69) vertices or sides of the central 12-gon and 168 edges. This pattern of numbers exists only for an axis passing through two diametrically opposite A vertices because only for this type of axis do the vertices in the central plane perpendicular to it form a 12-gon. As for the 3:69:168 pattern in the two Type B dodecagons, in which the number 3 refers to three types of geometrical elements, so this number denotes the three types of vertices making up the disdyakis triacontahedron. As with the two dodecagons, it is not essential to specify here the set of three generic vertices, although — given that the A vertices at the extremities of the polyhedron located on the axis are the starting point and endpoint of its generation — it is natural to choose its uppermost A vertex and a B and a C vertex of one of the faces of the pyramid with a Golden Rhombic base immediately below it (see diagram). This is because the selection is consistent with the meaning of the number 3 in the 3:69:168 pattern as the source or starting point of the four sacred geometries discussed earlier. Which of the four faces of the topmost pyramid is chosen to represent the number 3 is unimportant. What is crucial here is that the disdyakis triacontahedron provides a natural representation of it as the three types of vertices, thereby manifesting the 3:69:168 holistic pattern.
The fact that the disdyakis triacontahedron embodies the holistic parameter 240 as the 240 points & lines that surround any axis and displays the same 3:69:168 pattern as the sacred geometries discussed above is yet more confirmation that it is the polyhedral expression of the universal mathematical paradigm that is found in them.
| << Previous 1... 32 33 [34] 35 36 ...40 Next >> |