| << Previous 1... 33 34 [35] 36 37 ...40 Next >> |
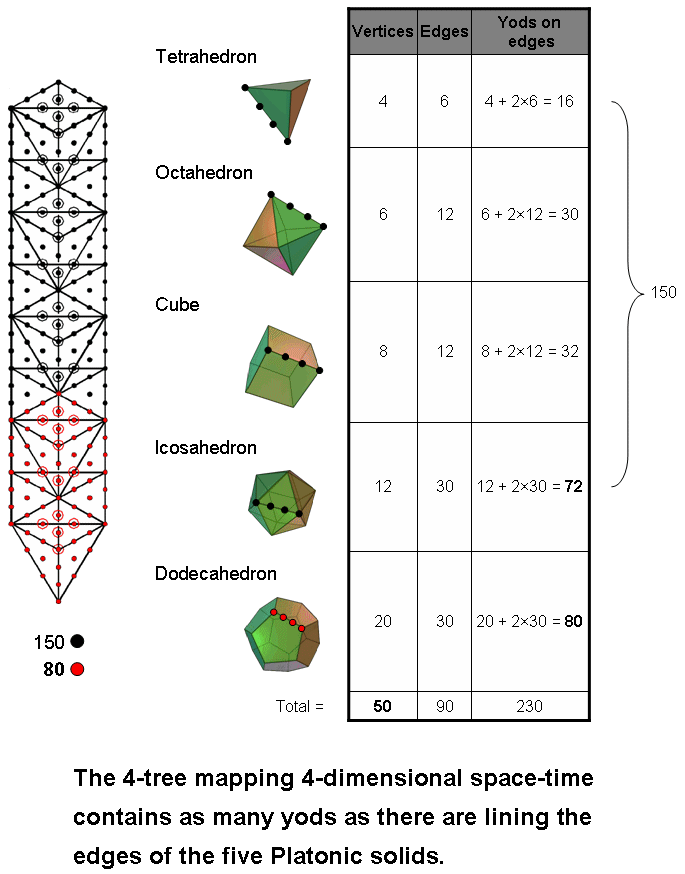
#35 A correspondence between the 4-tree and the five Platonic solids

The number of yods in the n-tree is Y(n) = 50n + 30. The 1-tree (the lowest Tree in any set of overlapping Trees) has Y(1) = 80 yods. They are coloured red in the diagram opposite. The 4-tree has Y(4) = 230 yods. They comprise the 80 red yods in the 1-tree and 150 black yods in the three Trees above it. 80 is the number value of Yesod, the penultimate Sephirah of the Tree of Life.
When the 50 faces of the five Platonic solids are divided into their sectors and the latter turned into tetractyses, there are four yods lining each of their 90 edges. Two of these yods are hexagonal yods and two are vertices. The number of yods lining their edges = 50 + 90×2 = 230. The table indicates that 80 red yods line the 30 edges of the dodecahedron, so that the first four solids have 150 black yods lining their 60 edges. The diagram depicts four yods on a representative edge of each Platonic solid.
The following correspondences exist between the 4-tree and the five Platonic solids:
The five Platonic solids are the five regular polyhedra that are, mathematically speaking, allowed to exist in 3-dimensional space, that is, in 4-dimensional space-time. This is mapped by the 4-tree, each Tree denoting one of the four dimensions. It is the reason for the existence of the correspondence. This property is an example of the Tetrad Principle in action, for it is the yod population of the lowest four Trees that determines how many yods are needed to shape the holistic set of the five regular polyhedra. It is formulated in Article 1. The number of yods in n overlapping Trees of Life = 50n + 20. Hence, four overlapping Trees contain 220 yods. The counterpart of this in the yods lining the edges of the five Platonic solids is the 220 yods that surround axes passing through their centres and pairs of opposite vertices.
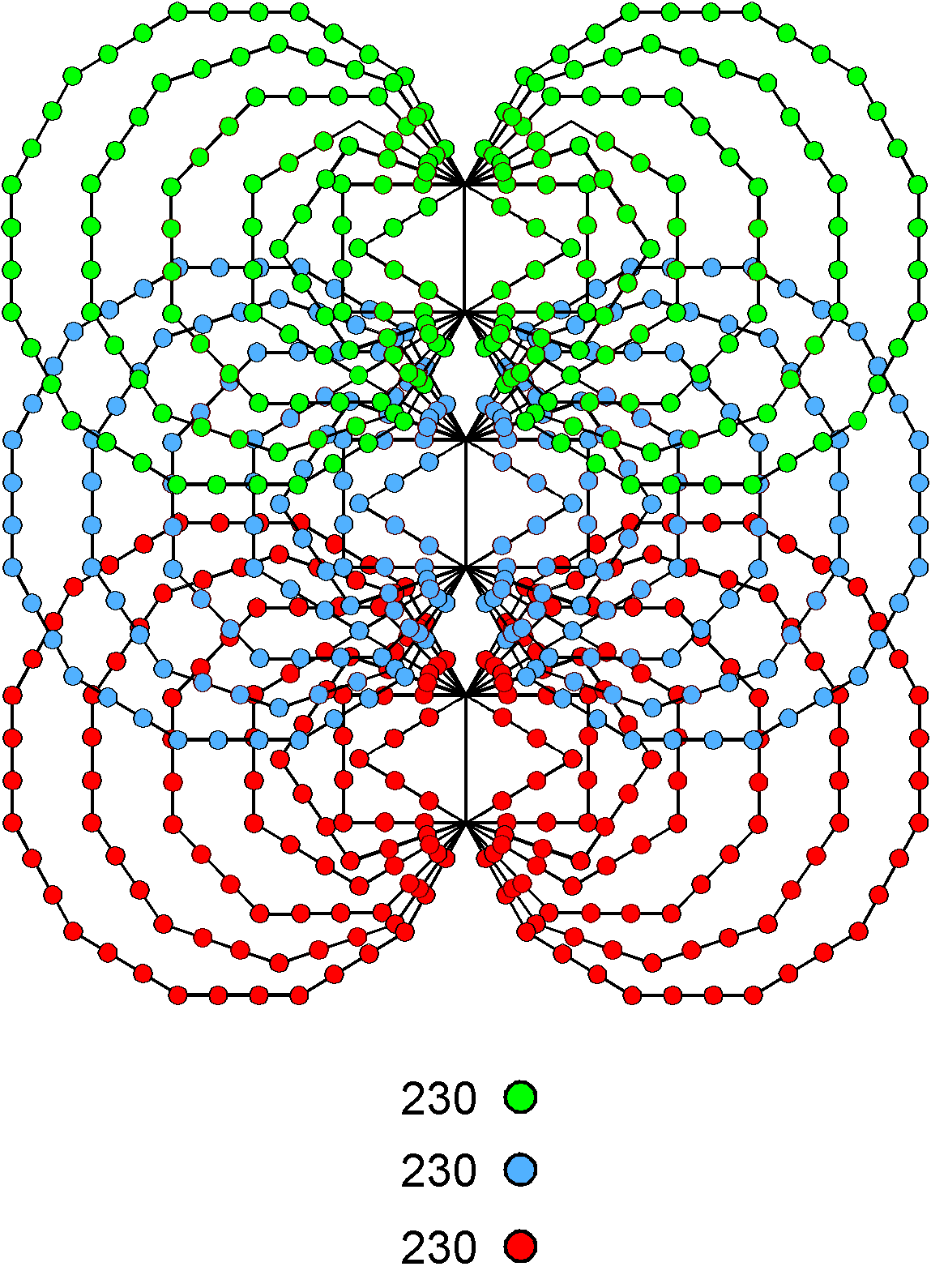
When the 94 sectors of the (7+7) enfolded polygons of the inner Tree of Life are tetractyses, 236 yods line the sides of the polygons (see #8). 232 boundary yods are outside their shared root edge, which has four yods. Of these, the topmost corners of the two hexagons coincide with the lowest corners of the hexagons enfolded in the next higher Tree of Life. This means that 230 yods shaping the polygonal inner Tree of Life are intrinsic to each set of 14 polygons (see the diagram shown above). The number that quantifies the shape of the five Platonic solids also determines the form of the inner Tree of Life in terms of the unshared sides of the 14 polygons. The sides of the pair of square & dodecagons are lined by 80 yods, leaving 150 yods that line the other polygons. This demonstrates how holistic systems possess the same parameters, which divide into analogous patterns of other numbers.
| << Previous 1... 33 34 [35] 36 37 ...40 Next >> |