| << Previous 1... 36 37 38 39 [40] Next >> |
#40 The n-gon as the polygonal counterpart of the outer & inner forms of n Trees of Life

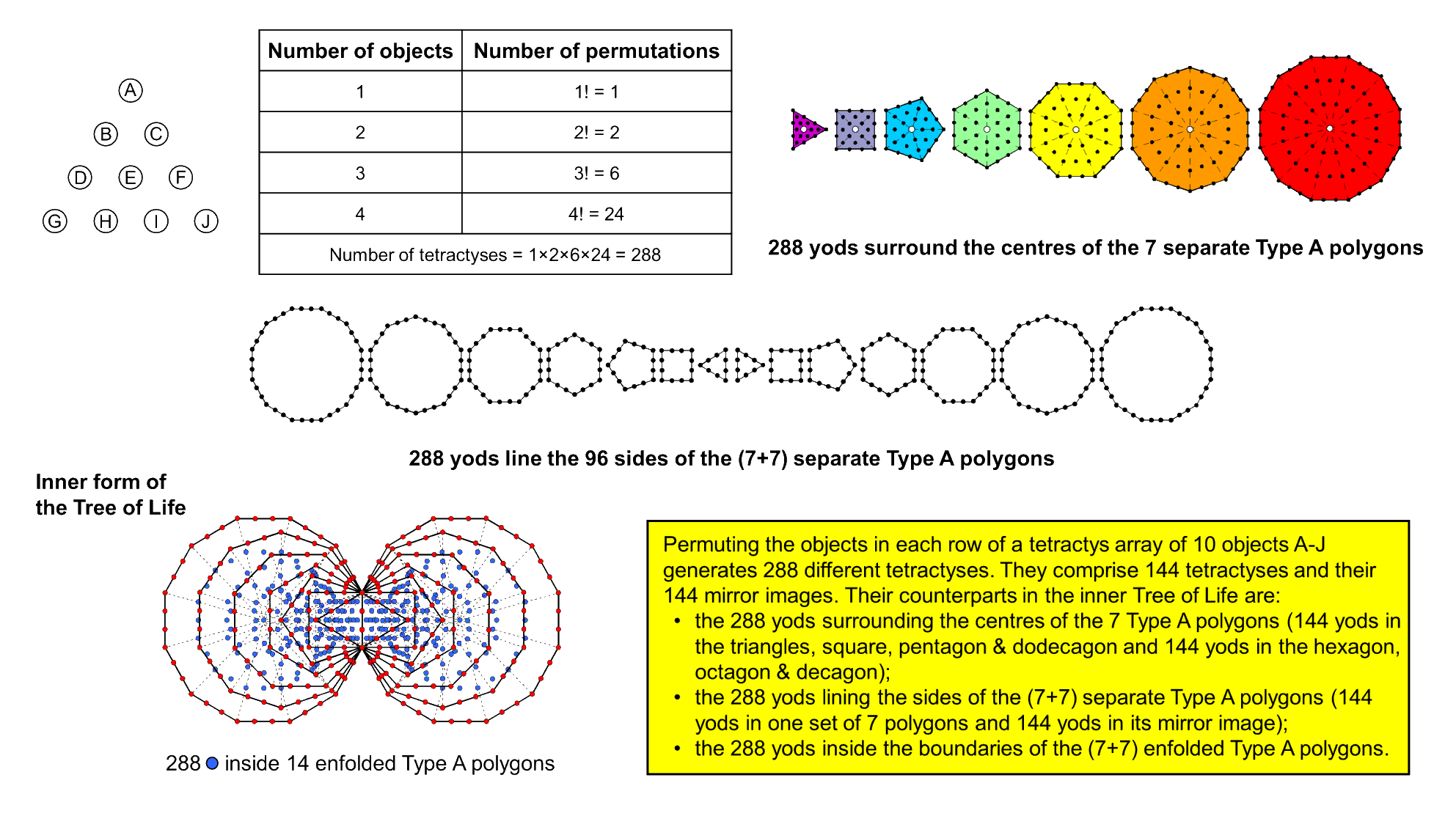
Consider 10 different objects labelled A, B, C, D, E, F, G, H, I & J. Let us arrange them so as to form a tetractys, i.e., four rows of 1, 2, 3 & 4 objects. N objects can be arranged in N! (=1×2×3×....N) ways. The one object A in the first row has only one (=1!) arrangement, the two objects B & C in the second row has two (=2!) orderings, the three objects D, E & F in the third row have six (=3!) permutations and the four objects (G, H, I & J) in the fourth row have 24 (=4!) permutations. The number of tetractyses that we can generate by permuting the objects in all rows = 1!×2!×3!×4! = 1×2×6×24 = 288. This can be written as a tetractys array of the first four powers of 1, 2, 3 & 4:
|
10 |
||||
| 21 | 21 | |||
|
288 = 11 + 22 + 33 + 44 = |
32 |
32 |
32 |
|
| 43 | 43 | 43 | 43 |
That this is possible is no coincidence because the number 288 is one of the parameters of the inner Tree of Life (as we shall show next). Being a parameter of holistic systems, it conforms to the Tetrad Principle discussed in Article 1. As
| 3 | 5 | 7 | 9 | |
|
288 = 172 − 1 = |
11 | 13 | 15 | 17 |
| 19 | 21 | 23 | 25 | |
| 27 | 29 | 31 | 33 |
this number is the sum of the first 16 odd integers after 1, where 16 = 42 (notice the appearance of the masonic number 33 here as the largest of the first 16 odd integers after 1). The Tetrad determines it geometrically because 288 is the number of yods surrounding the centre of a square (symbol of the number 4) whose sectors are 2nd-order tetractyses:
| 288 = |  |
The number of yods surrounding the centre of the Type A n-gon with tetractyses as its sectors is 6n. The seven types of regular Type A polygons making up the inner Tree of Life have 48 corners, so that their centres are surrounded by (6×48=288) yods when they are separate, not enfolded. When permuted within each row, the 10 different objects can generate as many tetractyses as there are yods surrounding the centres of the seven Type A polygons. It is as though each yod that shapes a polygon symbolises one of the 288 possible tetractyses that can be generated by re-arranging the objects in each row of a tetractys. As discussed in Article 64, the seven types of polygons form two sets of polygons, each having 24 corners, so that 48 = 2×24 and 288 = 48×6 = 2×6×24. But this is precisely the factorisation discussed above that arises from permuting the objects in each row of a tetractys. The factor of 2 expresses the two "halves" of the seven polygons, each with 24 corners, and the factor of 6 expresses the six yods per tetractys sector. The four rows of the tetractys symbolise the trunk of the outer Tree of Life:
point
line with two endpoints
triangle with three corners
tetrahedron with four vertices
They are the first four simplexes: 0-simplex, 1-simplex, 2-simplex & 3-simplex. Re-arranging objects in a tetractys is analogous to permuting pairs of 0-simplexes belonging to each simplex. Associated with the n-simplex with (n+1) vertices are (n+1)! ordered n-simplexes. The permutation numbers 1, 2, 6 & 24 are the numbers of ordered simplexes associated with the first four simplexes forming the trunk of the Tree of Life. The six yods intrinsic to each sector consist of three yods lining a side of the polygon and three internal yods. Their counterpart is the six permutations of the three objects in the third row, which comprise three permutations and their mirror images. As 2 = 1×2, 6 = 3×2 and 24 = 12×2, 288 = 2×6×24 = 1×3×12×23 = 36×8. The number value 36 of ELOHA, the Godname of Geburah, is the number of tetractyses that get doubled in turn in the second, third & fourth rows because half of the permutations of objects in these rows are the mirror images of the other half.
The 288 tetractyses consist of 144 tetractyses and 144 others whose rows are the mirror images of the former. The inner Tree of Life counterpart of this division into 144 chiral pairs of tetractyses is the 144 yods that line the sides of the seven polygons forming each half of it, one set of polygons being the mirror image of the other set.
The seven enfolded Type A polygons have 264 yods. Lining their sides are 120 red yods, leaving 144 blue yods inside them. The inner Tree of Life has 288 yods inside its 14 polygons, 144 yods being in each half.
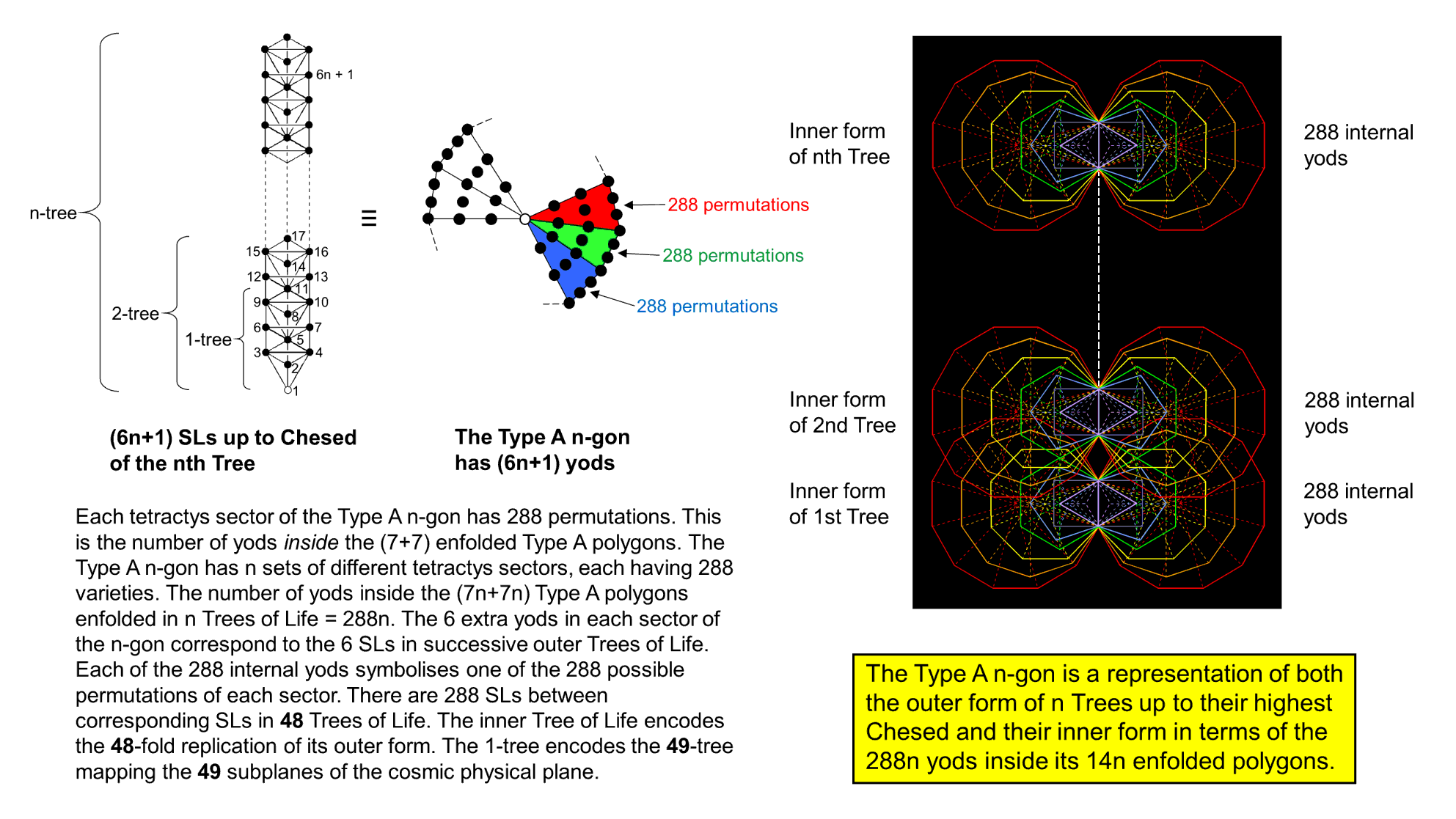
The n-gon has (6n+1) yods, where "1" denotes its centre. This yods symbolises Malkuth of the lowest Tree. The yods symbolise the (6n+1) SLs up to Chesed of the nth Tree. Each tetractys sector of a Type A n-gon has 288 permutations of its 10 yods, of which six yods are intrinsic to it. They denote the six SLs added by successive, overlapping Trees of Life. The 288 permutations correspond to the 288 permutations of the trunk of each Tree as the sequence of the first four simplexes. The yods in the Type A n-gon correspond to the 0-simplexes ("vertices") making up the n trunks in n overlapping Trees up to the first Sephirah of Construction of the nth Tree. 288 yods are inside the (7+7) Type A polygons enfolded in each Tree as its inner form. They symbolise the 288 ways of labelling the trunk of its corresponding outer Tree. Just as the yods of the Type A n-gon symbolise the outer form of n overlapping Trees up to Chesed of the nth Tree so, too, its n sets of 288 permutations of its yods symbolise the n sets of 288 yods that are inside the 14n polygons of the inner form of n Trees.
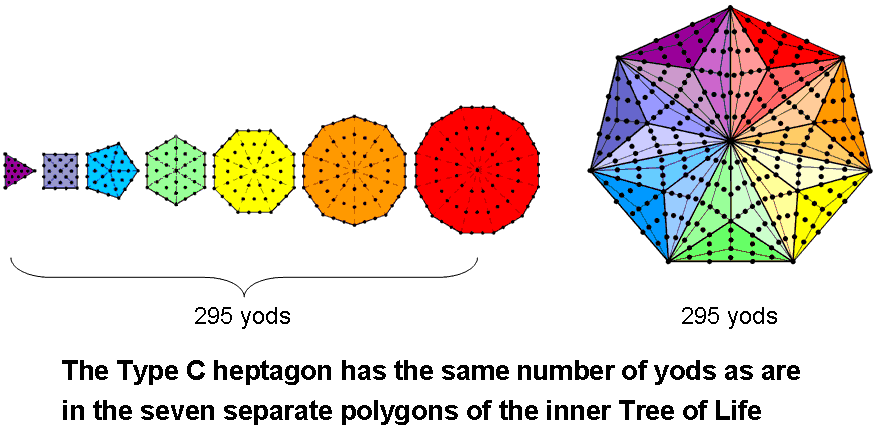
Including their seven centres, the seven types of polygons contain (7+288=295) yods. This is the number of SLs up to Chesed of the 49th Tree. These centres symbolise the seven SLs up to Chesed of the 1-tree. There are also 295 yods in the Type C heptagon, its seven corners corresponding to these centres:
The 288 yods surrounding the centres of the seven Type A polygons symbolise the 288 SLs beyond the lowest Chesed up to Chesed of the 49th Tree. This is the way in which the inner form of the Tree of Life encodes the 48-fold replication of its outer form. As explained in the section Maps of Reality/Cosmic Tree of Life, there are seven cosmic planes of consciousness with 91 subplanes. The lowest cosmic plane is the cosmic physical plane, which has 49 subplanes mapped by 49 Tree of Life. The 1-tree maps the lowest of these subplanes. Its inner form encodes all 49 subplanes of the cosmic physical plane. The five polygons in the second set of polygons other than the triangle and square encode the 42 subplanes of the six cosmic superphysical planes. They have 246 yods surrounding their centres, where 246 is the number value of Gabriel, the Archangel of Yesod, whose Godname is EL CHAI, which has the number value 49. This is how the Godname and Archangel of Yesod determine the division between the physical and superphysical cosmic planes. The number 80 of Yesod, meaning "foundation," is the number of corners of the 94 sectors of the (7+7) enfolded Type A polygons. The (7+5=12) enfolded Type A polygons that encode the seven cosmic planes have 87 sectors, where 87 is the number value of Levanah, the Mundane Chakra of Yesod.
(Work in progress)
| << Previous 1... 36 37 38 39 [40] Next >> |