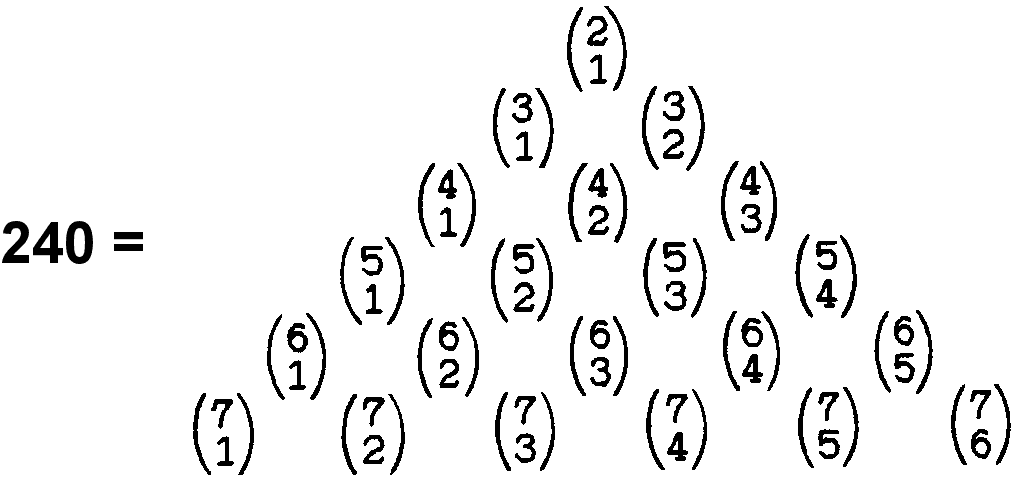Home
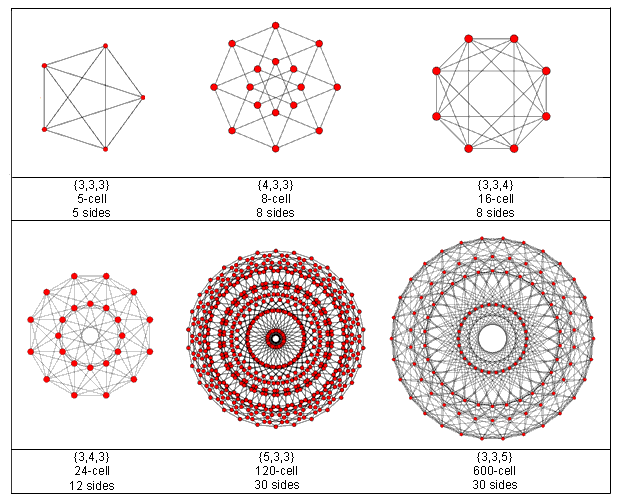
2. The 10×24 division in sacred geometries & its realisation in the 421 polytope representing the 240 roots of E8
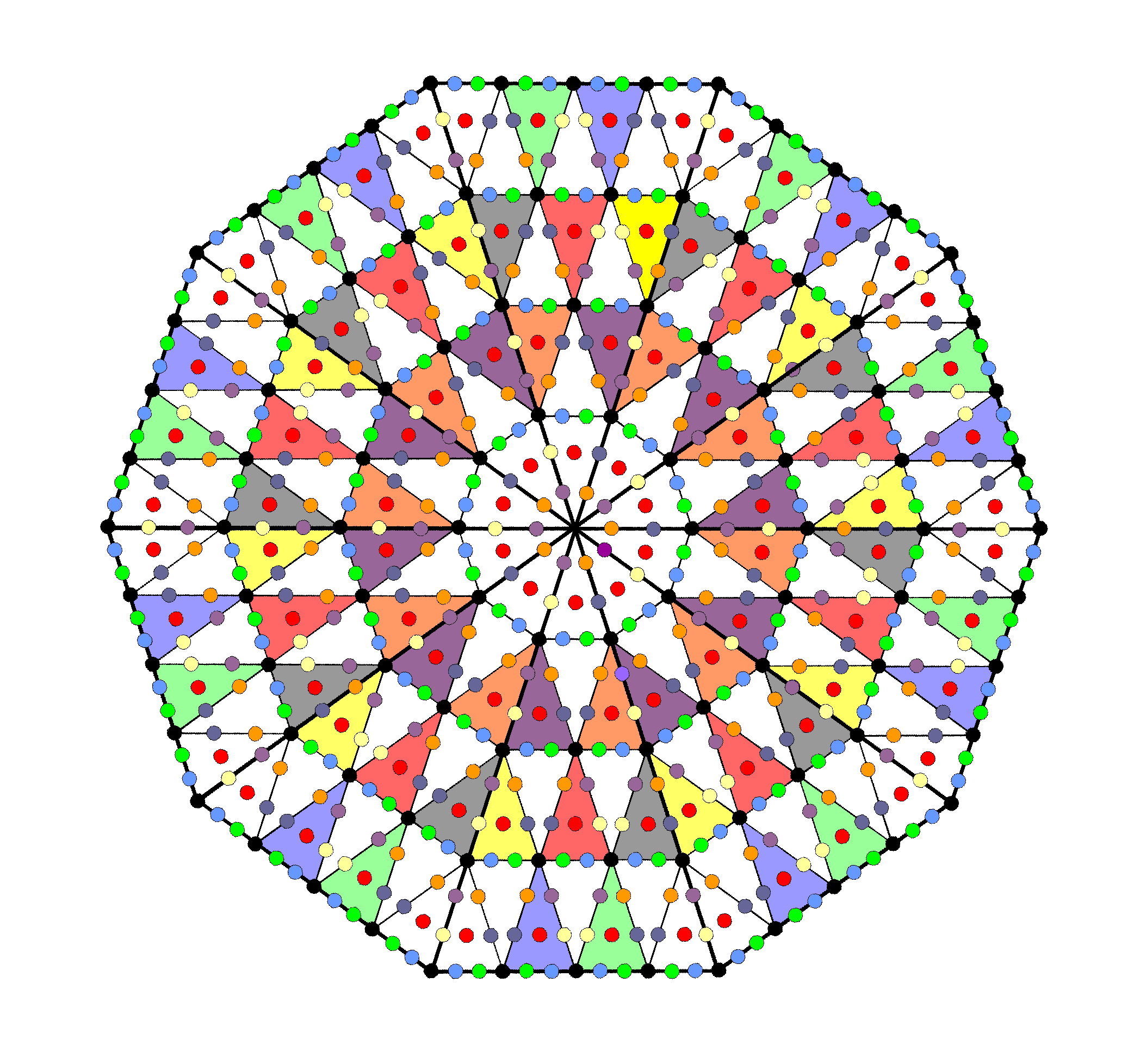
Article 53 explains how the structural elements (yods or points, lines &
triangles) of 2-dimensional and 3-dimensional sacred geometries divide in a non-trivial way into 10 sets of 24
elements. The table below summarises this 10-fold pattern.
|
The 4 light grey and 3 dark grey Type A regular
polygons of the inner Tree of Life have (120+120=240) hexagonal yods.
|
The 7 polygons with 3, 4, 5, 6, 8, 10 & 12 corners
can form 2 subsets, each with 24 corners, in 2
different ways:
(3+4+5+12) + (6+8+10)
(3+5+6+10) + (4+8+12).
However, given the analogy between the 7 polygons
and the 7 Sephiroth of Construction which, in order of emanation, form two triads and a singlet,
only the first way is consistent with this 3:3:1 pattern
because the second way has one of the polygons (square) in the first triplet of polygons (coloured light grey) being grouped with the
octagon in the second triplet S′ of polygons (dark grey), which violates this pattern. The triangle, square
& pentagon have 12 sectors with (12×5=60) hexagonal
yods, as does the dodecagon. The set of these 4 polygons will be called "S." The hexagon, octagon
& decagon in S′ have 24 sectors with (24×5=120) hexagonal
yods. The 7 polygons contain 240 hexagonal yods made up of 120 hexagonal yods in
S and 120 hexagonal yods in S′. They are distributed 5 per sector, coloured red, orange, yellow, green &
blue. Each colour is repeated 24 times in S (write the set
as 24) and 24
times in S′ (write it as 24′). Hence, the 240 hexagonal yods naturally
group into 5 sets
of 24 and
5 sets
of 24′, i.e., 10 sets of 24 hexagonal yods:
240 = 120 + 120′,
where
120 = 5×24 and 120′ = 5×24′.
|
|
120 yods as 10 sets of 12 line the sides of each
separate set of seven enfolded Type A polygons.
|
Taken separately, the two halves of the inner form of
the Tree of Life consist of 7 regular polygons enfolded in one another so that they have
36 corners. These form 3 sets of 12:
- dodecagon: 12 white corners;
- triangle, pentagon & decagon: 12 light grey
corners;
- square, hexagon & octagon: 12 dark grey
corners.
The 84 hexagonal yods on the sides of
each set of 7 enfolded polygons form 7 sets of 12:
- The 2 sides of the triangle outside the root edge have 4
violet hexagonal yods. The 4 external sides of the pentagon have 8 violet hexagonal yods.
Hence, the 2 polygons have 12 violet hexagonal yods;
- The 5 external sides of the
hexagon have 5 indigo hexagonal yods and the 7 external sides of the octagon have 7 indigo
hexagonal yods. Hence, these 2 polygons have 12 indigo hexagonal yods;
- The 5 external sides of the
hexagon and the 7 external sides of the octagon have 12 blue hexagonal
yods;
- The 3 external sides of the
square and the 9 external sides of the decagon have 12 green hexagonal
yods;
- The 3 external sides of the
square and the 9 external sides of the decagon have 12 yellow hexagonal
yods;
- The 12 sides of the dodecagon
have 12 orange hexagonal yods;
- The 12 sides of the dodecagon
have 12 red hexagonal yods.
The 120 yods on the boundary of each set of enfolded polygons form
10 sets of 12 yods. Both sets of enfolded polygons form 10 sets of 24 yods.
|
10 classes of 24 geometrical elements surround the centres of the triangle, square,
pentagon & dodecagon, as well as the centres of the hexagon, octagon & decagon.
|
Each sector of a Type B n-gon is a Type A triangle. It
has 10 geometrical elements per sector surrounding the centre of the n-gon:
- black, polygonal corner;
- grey polygonal side;
- white, radial side;
- red corner shared by 3 triangles;
- orange side of triangle;
- yellow side of triangle;
- green side of triangle;
- blue triangle;
- indigo triangle;
- violet triangle.
Surrounding the centres of the Type B triangle,
square & pentagon are 120 geometrical elements that form 10 classes of 12. Surrounding the
centre of the Type B dodecagon are 120 geometrical elements in 10 classes of 12 elements. The
centres of the 4 polygons in S are surrounded by 240 geometrical elements that form 10 classes of
24, as are the centres of the 3 polygons in S′. The 10 classes of geometrical elements comprise 5
points & triangles and 5 lines. Hence, the 240 geometrical elements in S or S′ consist of 5
sets of 24 points & triangles and 5 sets of lines, i.e., 10 sets of 24 geometrical
elements.
|
|
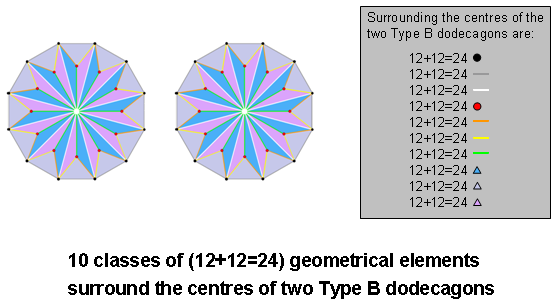
|
Surrounding the centre of the Type B dodecagon are
120 geometrical elements. They consist of 5 sets of 12 points & triangles and 5 sets of 12
lines, i.e., 5 sets of 24 geometrical elements. The 240 geometrical elements that surround the
centres of 2 separate Type B dodecagons consist of 10 sets of 24 geometrical elements, i.e., 5 sets
of 24 points & triangles and 5 sets of 24 lines.
|
|
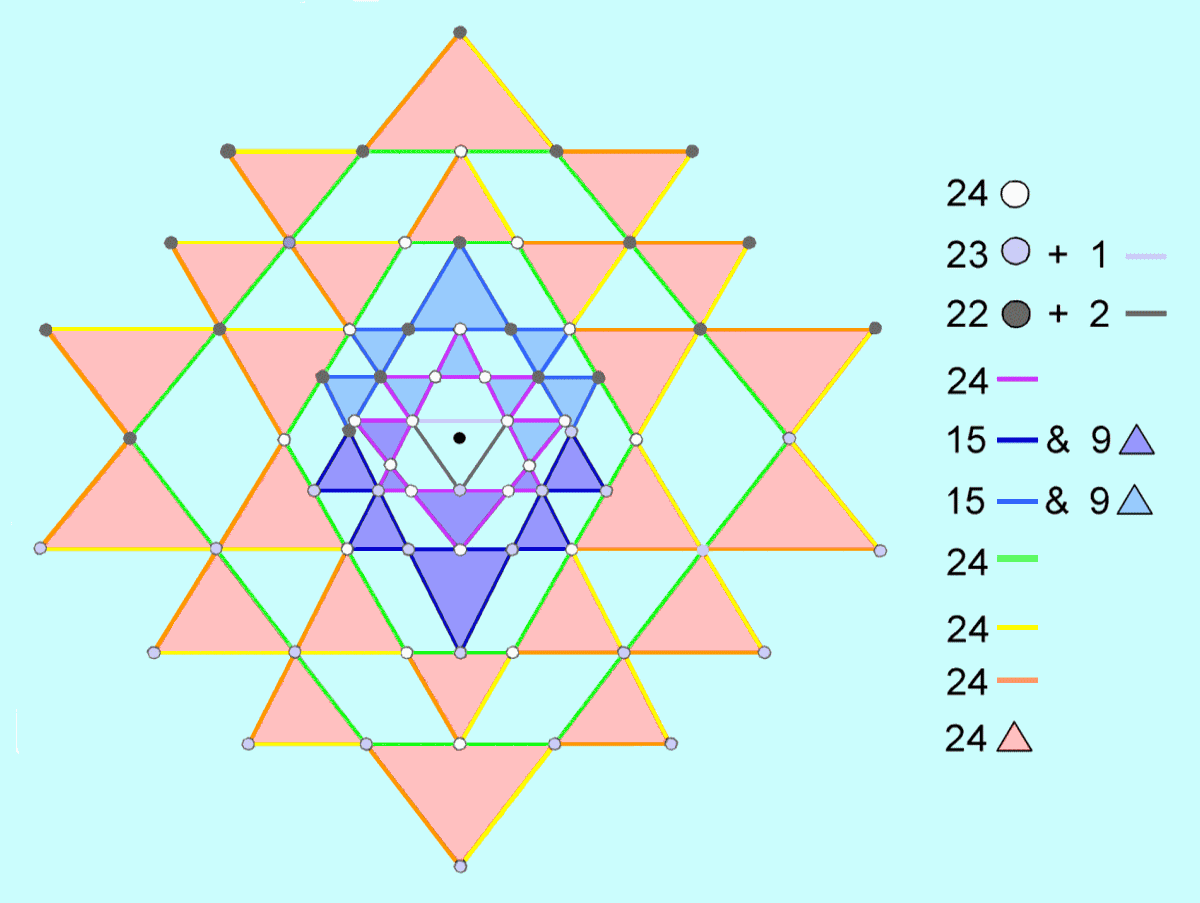
Surrounding the centre of the 2-d Sri Yantra are
10 sets of 24 geometrical elements.
|
In the 2-dimensional Sri Yantra, the most
well-known yantra in Hindu Tantra,
9 triangles (5 downward-pointing triangles, four
upward-pointing triangles) are interlaced in such a way as to generate 43 smaller triangles. Arranged around a central triangle are 42
triangles. They form 4 groups: 8, 10, 10 & 14 triangles. At the centre of the central
triangle is a point, or bindu, from which all levels of existence emanate. Because this point
lies in the plane of the central triangle and is a distinct point, the latter is not a true triangle
like the 42 other triangles in the true mathematical sense of being an area filled with
points and bounded by 3 straight lines. It is, simply, a triangular boundary composed of 3
points and 3 straight lines. The table below lists the number of corners (points), sides of
triangles (lines) & triangles in the 2-d Sri Yantra.
| |
Number of
corners
|
Number of
sides
|
Number of triangles
|
Total
|
|
Central 'triangle'
|
1
|
3
|
0
|
4
|
|
1st group of triangles
|
4 + 8 = 12
|
8×3 = 24 |
8 |
44 |
|
2nd group of triangles
|
6 + 10 = 16
|
10×3 = 30
|
10
|
56
|
|
3rd group of triangles
|
2 + 10 = 12
|
10×3 = 30
|
10 |
52
|
|
4th group of triangles
|
28
|
14×3 = 42
|
14
|
84
|
|
Total
|
69
|
129
|
42 |
240 |
For purposes of counting corners, the two upper
corners of the central 'triangle', which coincide with the points of contact of 2 pairs of
triangles, are included with the first group of triangles. Including the lowest corner of the
central 'triangle,' 69 points surround the centre of the 2-d Sri Yantra, as well
as 129 lines & 42 triangles. The 240 geometrical elements surrounding the
centre comprise 3
lines belonging to the central triangle and 69 points, i.e., 72 points & lines,
and 168 lines & triangles. The former divide into 3 sets of 24 and the latter
divide into 7 sets of 24:
- 1st & 3rd groups have 24 white corners;
-
Central 'triangle', 2nd & 4th groups
comprise 22 light grey corners in one half of
Sri Yantra, lower light grey corner &
upper light grey side of central
'triangle';
- Central 'triangle', 2nd & 4th groups comprise 22 dark grey
corners in other half & 2 dark grey sides of central 'triangle';
- 3rd & 4th groups comprise 24 red
triangles;
- 3rd & 4th groups comprise 24
orange sides;
- 3rd & 4th groups comprise 24 yellow
sides;
- 3rd & 4th groups comprise 24 green
sides;
- 1st & 2nd groups comprise in one half of Sri
Yantra 15 blue sides & 9 blue triangles, i.e., 24 blue sides & triangles;
- 1st & 2nd groups comprise in other half 15 indigo sides & 9
indigo triangles, i.e., 24 indigo sides & triangles;
- 1st group comprises 24 violet sides.
The 240 points, lines & triangles comprise 10
sets of 24. The lack of mirror symmetry about the horizontal axis passing through the bindu of the
distribution of 42 triangles around the central one means
that not every set of 24 geometrical elements belonging to them can divide about this axis into two sets of 12. However, the diagram
is symmetric about the vertical axis passing through the bindu and the 9 tips of
the downward-pointing and upward-pointing triangles in the central column. Division by this central, vertical axis into two sets
of 120 geometrical elements — one set the mirror image of
the other — is meaningful provided that the 13 points, lines & triangles in
the half of the Sri Yantra above the bindu that are
aligned with this axis be formally associated with one half (left or right) of the diagram and
their 13 counterparts in the half below the bindu be
associated with the other half (right or left) of the diagram. Notice that YAHWEH with number value
26 prescribes the number of geometrical elements spanning this vertical
axis.
|
|

The faces of the first three Platonic solids, the
icosahedron & the dodecahedron have 10 sets of 24 hexagonal yods.
|
The hexagonal yod populations in the faces of the 5
Platonic solids.
| Platonic
solid |
Edges |
Faces
|
Hexagonal yods
at centres
|
Hexagonal yods
on edges |
Hexagonal yods
on interior sides |
Total |
|
Tetrahedron
|
6
|
4
|
4×3 = 12 |
6×2 = 12
|
4×6 = 24 |
48 |
|
Octahedron
|
12
|
8 |
8×3 = 24 |
12×2 = 24 |
8×6
= 48
= 2×24 |
96 |
|
Cube
|
12
|
6
|
6×4 = 24
|
12×2 = 24
|
6×8 = 48 =
2×24 |
96 |
|
Subtotal
|
30
|
18
|
60 |
60
|
120 |
240 |
|
Icosahedron
|
30
|
20
|
20×3 = 60
|
30×2 = 60
|
20×6 = 120 |
240 |
|
Subtotal
|
60
|
38
|
120 |
120 |
240 |
480 |
| Dodecahedron |
30 |
12 |
12×5 = 60 |
30×2 = 60 |
12×10 = 120 |
240 |
| Total |
90 |
50 |
180 |
180 |
360 |
720 |
When their 50 faces are constructed from
tetractyses, the 5 Platonic solids have (720=6!) hexagonal yods. They are of 3 types: 1. hexagonal
yods at centres of tetractyses; 2. hexagonal yods on edges of polyhedra, and 3. hexagonal yods on
sides of tetractyses inside the polygonal faces. The first 3 Platonic solids have 240 hexagonal
yods comprising 120 red hexagonal yods either at centres of tetractyses or on edges and 120
turquoise hexagonal yods on interior sides, as indicated in the pink row in the table. The
former comprises (12+12=24) hexagonal yods at the centres of the faces of the tetrahedron or on its
edges and 4 sets of 24 hexagonal yods either at centres or on edges, i.e., 5 sets of 24 hexagonal
yods. The tetrahedron has 24 hexagonal yods on interior sides, whilst the octahedron
has 48 such hexagonal yods (24 in each half), as does the cube. So the first 3
Platonic solids have 5 sets of 24 hexagonal yods on the interior sides of tetractyses in their
faces. Altogether, they have 10 sets of 24 hexagonal yods that are made up of 2 groups of 5
sets of 24 yods (see the table shown above):
240 = 120 + 120 = [(12+12) + 24 + 24 + 24 + 24] +
[24 + 2×24 + 2×24].
This 120:120 division in the 240 hexagonal yods in
the faces of the first 3 Platonic solids re-occurs in both the icosahedron and the dodecahedron
because they both have 120 hexagonal yods of the first two types and 120 hexagonal yods of the
third type. Alternatively, each half of either polyhedron has (30+30+60=120) hexagonal yods (see
the blue & red rows in the table).
|
|

10 sets of 24 vertices & edges surround an axis
of the disdyakis triacontahedron.
|
The so-called "Catalan solids" are the duals of the
more well-known Archimedean solids. The disdyakis triacontahedron is the Catalan solid with the
most faces. It has 62 vertices. They are of three types: 30 A vertices are peaks
of pyramids with Golden Rhombi as their bases. 12 B corners of these pyramids are vertices of
an icosahedron with 20 triangular faces and their remaining 20 C corners are vertices of a
dodecahedron with 12 pentagonal faces. If one imagines a straight line passing through two
diametrically opposite B vertices of the disdyakis triacontahedron, then 30 A vertices, 10 B
vertices & 20 C vertices surround this axis. 3 A vertices surround the C vertex at the centre
of each icosahedral face with B vertices at its corners. This means that the 30 A vertices can be
grouped into 10 sets of 3 belonging to the 10 pairs of opposite faces. The 60 vertices surrounding
the B-B axis form 10 sets of 3 A vertices, 10 sets of one B vertex and a pair of diametrically
opposite C vertices, i.e.,
30 A + 10 B + 20 C =
10×(3 A + B + 2 C).
The polyhedron has 180 edges (60 AB edges, 60 BC
edges & 60 AC edges). The 20 equilateral triangles
with B vertices at its corners are the faces of the
underlying icosahedron, so that 3 AC edges are associated
with each such triangle. Each
icosahedral face has its diametrically opposite one. This
means that there are 10 pairs of these triangles, i.e., 10 sets of 6 AC edges. A B vertex is the centre of a pentagonal face of the underlying dodecahedron. 5 AB edges meet at these centres, of
which there are 6 pairs of diametrically opposite ones. The 60 AB edges
therefore group into 10 sets of 6. Similarly, 5 BC
edges meet at these centres, so that the 60 BC edges group into 10 sets of 6. The 180 edges
group into 10 sets of (6 AB + 6 BC + 6 CA), i.e.,
60 AB + 60 BC + 60 CA = 10×(6 AB + 6 BC + 6
CA).
The (60+180=240) vertices & edges surrounding the B-B axis
group into 10 sets of 24 vertices & edges:
30 A + 10 B + 20 C + 60 AB + 60 BC + 60 CA = 10×(3 A
+ B + 2 C + 6 AB + 6 BC + 6 CA).
Of course, this property is true whatever the axis
is. But only in the case of a B-B axis are there 10 sets with identical geometrical compositions.
Surrounding the axis in each half of the disdyakis triacontahedron are 120 vertices & edges.
They are not grouped further into 10 identical sets of 12, because the odd numbers of
A and B vertices in each set of 24 means that they cannot be divided equally into sets of 12.
Instead, each half of the polyhedron is made up of 5 identical sets of 24 (=4×3×2×1)
geometrical elements. The equation 120 = 5! =
5×4×3×2×1 = 5×4×6 is
geometrically realised in the disdyakis triacontahedron because each of these 5
sets consists of 6 vertices and 3 sets of 6 edges, i.e., 4 sets of 6 vertices or
edges.
|
|
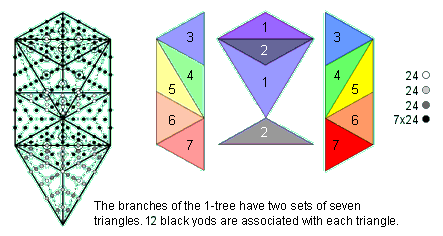
The 1-tree contains 10 sets of 24 yods that are not corners of its
19 Type A triangles.
|
The 1-tree contains 19 triangles with 11 corners
and 50 sides. When they are Type A triangles, each with 10 internal yods, 3 corners & 2 hexagonal yods on
every side, the number
of yods in the 1-tree = 11 + 25×2 + 19×10 = 251. It contains 240 yods other than corners representing Sephiroth. The
"trunk" of the 1-tree is the geometrical sequence:
- point (Kether);
- straight line (Chokmah-Binah Path);
- triangle (corners at Chesed, Geburah &
Tiphareth);
- tetrahedron (vertices at Netzach, Hod, Yesod &
Malkuth).
symbolised by the four rows of dots in the
Pythagorean tetractys. Excluding corners representing
Sephiroth, its yod population is tabulated
below:
The yod population of the trunk of the Tree of
Life.
| |
Corners |
Hexagonal yods at centres |
Hexagonal yods on sides of
triangles |
Total |
|
Point
|
0
|
0
|
0
|
0
|
|
Line
|
0
|
0
|
2
|
2
|
|
Triangle
|
1
|
3
|
12
|
4 + 12
|
|
Tetrahedron
|
4
|
12
|
12 + 24
= 36
|
4 + (12+12=24) + 24
|
|
Total
|
5
|
15
|
50
|
(2+4+4=10) + 12 + 24 + 24=
70
|
The "root" of the 1-tree is its Path connecting
Daath and Tiphareth, its projection onto the plane of the
(7+7) enfolded polygons making up the inner form of the 1-tree being their root edge.
Metaphysically, it is the interface between the outer form (trunk & branches) and inner aspects
of the Tree of Life encoding the former. As the endpoints of this Path are Sephiroth, the number of
non-Sephirothic yods in the root & trunk of the 1-tree = 2 + 70
= 72,
where
72 = (10+2=12) + 12 + 24 + 24 = (12+12=24) + 24 + 24.
The 72 yods comprise 3 sets of 24
yods. This leaves 168 yods in the
branches made up of 14 corners and 154 hexagonal yods in 14 Type A triangles with 2 hexagonal yods on each of
their 14 sides (there are 15 sides but one of these
is the root). There are 9 hexagonal yods inside each Type A triangle, so that
the 168 yods comprise 14 corners, 14 sets of 9 hexagonal yods and 14 pairs of
hexagonal yods. i.e., 14 sets of 12 yods, or 7 sets of 24 black yods. These sets are the 7
pairs of triangles making up the branches of the 1-tree, shown opposite as a dark & light
prismatic colour. 5 pairs of mirror-image triangles
numbered 3-7 are on opposite sides of the central Pillar of Equilibrium, which is straddled
by 4 triangles as 2 pairs. One pair can be associated with one half of the 1-tree and the
other pair can be associated with the other half (hence, they are depicted as light and dark
shades of indigo and violet). The 240 extra yods needed to construct the 1-tree from Type A
triangles comprise 10 sets of 24 yods — 3 sets in
its root & trunk and 7 sets in its branches. For
more details, see Article 53.
|
Given these remarkable correspondences between sacred geometries of various religions (as well
as in polyhedra both well and little studied), it cannot be doubted that the exceptional Lie group
E8 is central to the description of nature, for its number of roots is embodied in them all and it
is improbable in the extreme to dismiss this as coincidence! The analysis presented below will reinforce this
conclusion beyond all reasonable doubt.
The question raised by the embodiment in these sacred geometries of the number 240 and its
factorisation into 10 sets of 24 is this: do the 240 roots of E8 form 10 groups of 24 as well? If
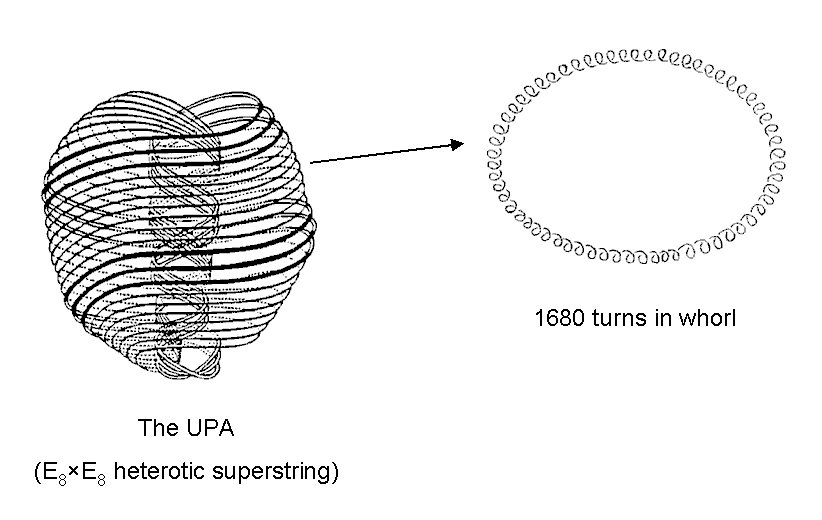
so, this would create a striking parallel with the UPA, whose 10 whorls, each making 10 half-revolutions around its
axis, were meticulously described by C.W. Leadbeater in the book Occult Chemistry that he co-authored
with Annie Besant and for which this website presents evidence that it is the subquark state of the
E8×E8 heterotic superstring. Indeed, it might amount to more than this. It might
actually be hard proof that the UPA is such a superstring, thereby disproving — through past research
by the author (see #12 in Occult Chemistry)
showing that the UPA is the constituent of quarks — the assumption made by most particle physicists that quarks
are superstrings.
The 421
polytope
Firstly, we need to consider a few geometrical concepts. A
skew polygon is a polygon whose vertices do not lie in a plane. Skew
polygons must have at least four vertices. A regular skew polygon has
equal edge lengths. A facet of a polyhedron is any polygon whose
corners are vertices of the polyhedron; it need not be a face. More generally, a facet of an n-polytope is an
(n–1)-polytope formed by some of its vertices. n-dimensional facets are also called n-faces. For example, a 0-dimensional face is a vertex of a polyhedron, a 1-face is a
1-dimensional edge and a 2-face is a 2-dimensional face of a polyhedron. In higher-dimensional geometry, the facets
of a n-polytope are the (n-1)-faces of dimension one less than the polytope itself. A Petrie polygon for a regular polytope of n dimensions is a skew polygon such that
every (n−1) consecutive sides (but no n) belong to one of the facets. For every
regular polytope, there exists an orthogonal projection onto a
plane such that one Petrie polygon becomes a regular polygon with the remainder of the projection interior to it.
The plane in question is the Coxeter plane of the symmetry group of the
polygon. Figure 1 shows the Petrie polygons for the five Platonic solids.

(Blue lines show "front" edges, black lines show "back"
edges.)
Figure 1. Petrie
polygons for the Platonic solids (red edges). Depicted here is their orthogonal projection as regular planar
polygons.
(uploaded by Tom Ruen to Wikipedia at http://commons.wikimedia.org/wiki/File:Petrie_polygons.png?uselang=en-gb
).
Figure 2 shows the
Petrie polygons of the six polychorons and the 421 polytope to be discussed shortly.
Figure 2. The Petrie polygons of the six polychorons
and the 421 polytope.
It is amusing that the pentagram, which the ancient followers of Pythagoras displayed on their
arms as a public sign of their membership in his brotherhood, should appear in the Petrie polygon of the 5-cell,
which is the simplest, 4-dimensional, regular polyhedron. They would certainly have approved, given their
emphasis of the central role of the number 4 in the mathematics that describes nature, as enshrined in the
author’s Tetrad Principle formulated in Article 1 and as demonstrated in
nearly every one of his previous articles! The Petrie polygon of this polyhedron is a simple pentagon because
the 5‑cell is dual to itself.
In 1900, Thorold Gosset (1869-1962), an English
lawyer and amateur mathematician, discovered an 8‑dimensional, semi-regular polytope that has proved to be
relevant to the theory of superstrings (or at least to the mathematics of one of the two symmetry groups
describing superstring forces). The n-face composition of the so-called "421 polytope" is shown below in Table 1:
Table 1. Numbers of n-faces in the
421 polytope.
|
Vertices
(0-faces)
|
Edges
(1-faces)
|
Faces
(2-faces)
{3}
|
Cells
(3-faces)
{3,3}
|
4-faces
{3,3,3}
|
5-faces
{3,3,3,3}
|
6-faces
{3,3,3,3,3}
|
7-faces
{3,3,3,3,3,3} + 411
|
Total
|
|
240
|
6720
|
60480
|
241920
|
483840
|
483840
|
207360
|
17280 +2160 = 19440
|
1503840
|
It has 6720 edges, where 6720 = 672×10.
Compare this with the fact that the first four Platonic solids:
tetrahedron, octahedron, cube &
icosahedron
have 672 yods when their faces and interiors
are constructed from tetractyses (see here). It is an amazing example of how the same parameters quantifying
global properties of holistic systems appear in different sacred geometries. Another example is the following:
suppose that we turn each triangular face into a
tetractys. The number of yods lining its edges = 240 + 6720×2 = 13680. As was pointed out in the earlier
discussion of the properties of the 120-cell (see comment 3), the (7+7) enfolded Type B polygons of the inner
Tree of Life have 1368 intrinsic yods, so that the (70+70) Type B polygons enfolded in 10 overlapping Trees of
Life have 13680 yods that are intrinsic to them (Fig. 3). We see that the
number measuring
.png)
Figure 3. The
inner form of 10 Trees of Life has as many yods as that which line the edges of the 421 polytope when
its 60480 faces are tetractyses.
the shape of the
421 polytope as the number of yods aligning its edges is exactly the same as the yod population of the
inner form of 10 overlapping Trees! Moreover, the (7+7) enfolded polygons have 26 yods that are either
centres or yods shared with the outer Tree. Of these, two yods are corners of hexagons that coincide with corners
of hexagons enfolded in the next higher Tree, so that 24 of these yods belong to each set of (7+7) polygons. It
means that 240 yods in the 140 polygons enfolded in 10
overlapping Trees of Life are either centres or shared. They correspond to the 240 vertices of the
421 polytope. (13680–240=13440) yods intrinsic to the (70+70) polygons surround their centres. They correspond to the 13440
hexagonal yods lining the 6720 edges of the 421. Such correspondences
make the conclusion seem inescapable that the 421 polytope central
to superstring theory has archetypal character because it is the polytope analogue of the inner form of 10
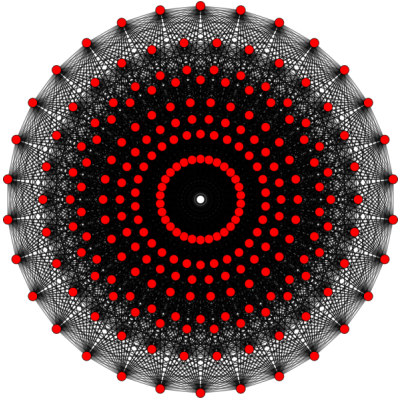
overlapping Trees of Life, each Tree representing a Sephirah. Figure 4 shows its projection onto
the E8 Coxeter plane.
.
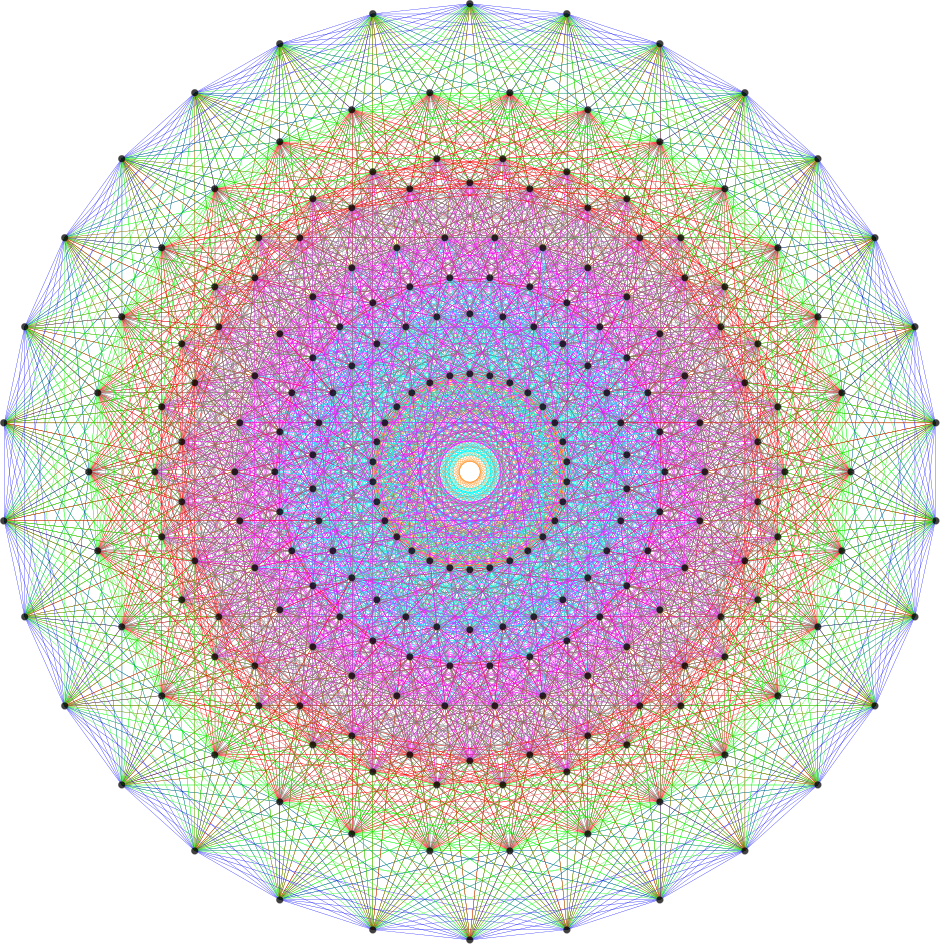
Figure 4. E8 Coxeter plane
projection of the 421 polytope.
This 4-dimensional projection of the
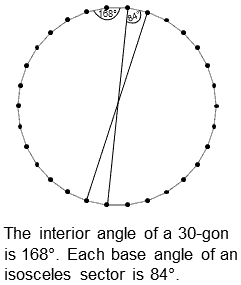
421 polytope is the compound of two 600-cells. The outer four red rings are four 30-gons with (4×30=120)
vertices of a 600-cell. The inner four blue rings denote the 120 vertices of a smaller 600-cell inside the larger
one. A 30-gon is the Petrie polygon for the 600-cell. Its interior angle is 168°. Each isosceles
triangular sector of the triacontagon has a base angle of 84°.
This 84:84 division is characteristic of the holistic parameter 168, being
found in numerous contexts throughout this website. That this number appears naturally in
the projected geometry of the 421 polytope, which mathematicians know represents the 240 roots of
E8, is strong evidence that the UPA is a state of the E8×E8 heterotic
superstring. Indeed, the same division manifests in the (120+720=840) vertices & edges in
each of the two 600-cells whose compound is the E8 Coxeter plane projection of the 421
polytope! Just as the internal angle of the triacontagon is (84+84=168°), so the number of
vertices & edges in the two 600-cells is (840+840=1680). See the section Triacontagon for how 30-gons embody the superstring
structural parameters 840 and 1680 paranormally ascertained by C.W. Leadbeater.
As found earlier, the
1200 faces of the 600-cell contains 9240 points, lines & triangles when constructed from Type A triangles. They
comprise the original 840 vertices & edges and 8400 new points, lines & triangles generated from
the seven points, lines & triangles inside each face. The 2400 faces of two such polytopes comprise (840+840=1680) vertices & edges
and (8400+8400=16800) new points, lines & triangles (4800 points or lines and 3600 triangles, or 4800 points or
triangles and 3600 sides). What this means is that 8400 geometrical elements are needed to construct the faces of
each 600-cell from simple triangles in a way that is consistent with the construction of other polytopes from
triangles — a requirement which demands that all polygonal 2-faces be divided into their sectors. They comprise
1×1200 points, 3×1200 lines and 3×1200 triangles, that is, 7×1200 geometrical elements. Many previous articles have
shown that this inner form embodies the numbers 840 and 1680, and now we encounter these very numbers in the
numbers of vertices & edges making up the two concentric 600-cells whose 240 vertices are root vectors of
E8. As these numbers are the numbers of circular turns in,
respectively, an outer or inner half of a helical whorl and a whole whorl, the inevitable conclusion to be drawn is
that the UPA is, indeed, an E8×E8 heterotic superstring the symmetry of whose forces is described by
E8. In other words, the 421 polytope embodies not only the 240 roots of E8 but also the number of circular turns in the 10 helical whorls along which the 240
E8 gauge charges are spread. Each of the 16800 circular turns would
correspond to one of the 16800 geometrical elements in the faces of the two 600-cells generated by their
construction from basic triangles. One of the 600-cells with 120 vertices and 840 vertices & edges would
correspond to the outer half of the UPA as its 10 whorls make 25 revolutions, the
2½ revolutions in each helical whorl comprising 840 turns,
and the other 600-cell with 120 vertices would correspond to its inner half as its 10 whorls make another 25
revolutions around its axis. The appearance of the numbers 840 and 1680 in the two 600-cells making up the
421 polytope is
strong evidence that the UPA is an E8×E8 heterotic superstring. The appearance of the numbers 8400 and 16800 in their
construction from Type A triangles is, so to speak, the “icing on the cake,” discrediting the possibility of
coincidence beyond all reasonable doubt. They refer to both the geometrical composition and the boundary yods
of the two 600-cells, for — as we found earlier — 8400 yods lining tetractyses in addition to those on edges
are needed to construct the faces of each 600-cell, so that (8400+8400=16800) new boundary yods are needed to
create the faces of both 600-cells making up the 421 polytope.
 |
 |
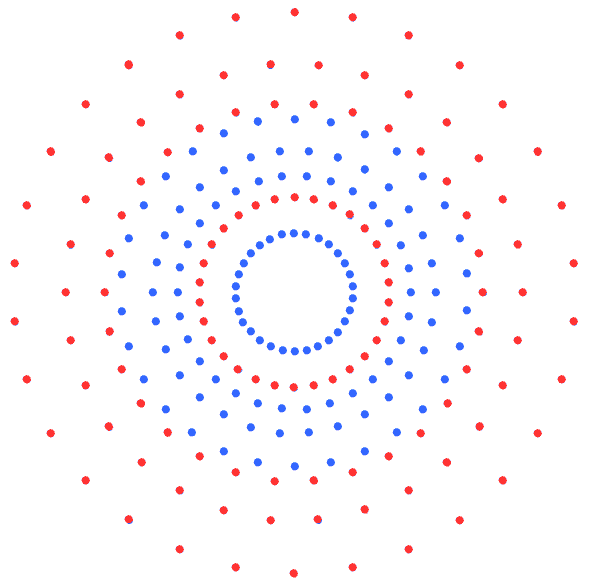
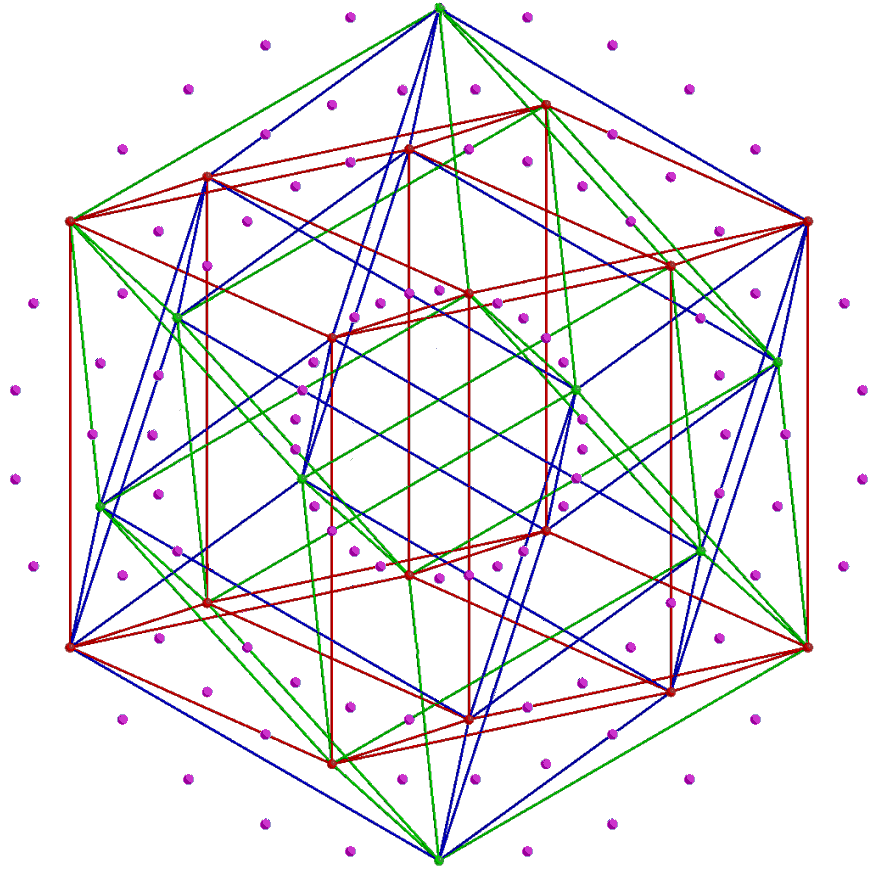 |
Figure 5. Zome model of the
600-cell as a compound of five 24-cells.
(Credit: http://homepages.wmich.edu/~drichter/five24cells.htm). |
3-dimensional projection of the 600-cell.
(Credit: "600-cell" by Jason Hise, uploaded to
Wikipedia.org.).
|
A 24-cell in the 600-cell. Shown are
the ×32 red, blue & green
edges of 3 hypercubes making up the 24-cell.
|
It is known to mathematicians that
the 120 vertices of a 600-cell can be portioned into those of five disjoint 24-cells, each with 24 vertices (Fig. 5). This compares with the fact that the dodecahedron with 20 vertices is a set of five
distinct tetrahedra. The two 600-cells comprise 10 disjoint 24-cells. This 10-fold character was shown in
Article 53 to be a
natural property of sacred geometries, indicating that it is the geometrical basis of either the 10 whorls of
the UPA or its 10 half-revolutions. A similar property now emerges in the geometry of the 421 polytope as the convex hull of two 600-cells. As we saw earlier, it has its striking counterpart in the inner form of 10 overlapping Trees of
Life as the 10 sets of 24 yods that are either centres of the
(70+70) enfolded polygons or shared with these Trees. This 10-fold pattern in the E8 lattice of 240 roots suggests that the whorl “carries” 24 E8 gauge charges corresponding to 24 roots that are represented by the 24
vertices of a 24-cell. The UPA would have 10 whorls because the two 600-cells consist of 10 disjoint
24-cells. Alternatively, a 24-cell could represent a half-revolution of all 10 whorls, the two 600-cells
determining the outer and inner halves of the UPA, each of which comprises 2½ revolutions of 10 whorls around the axis of the UPA, the five half-revolutions being
represented by the five 24-cells.
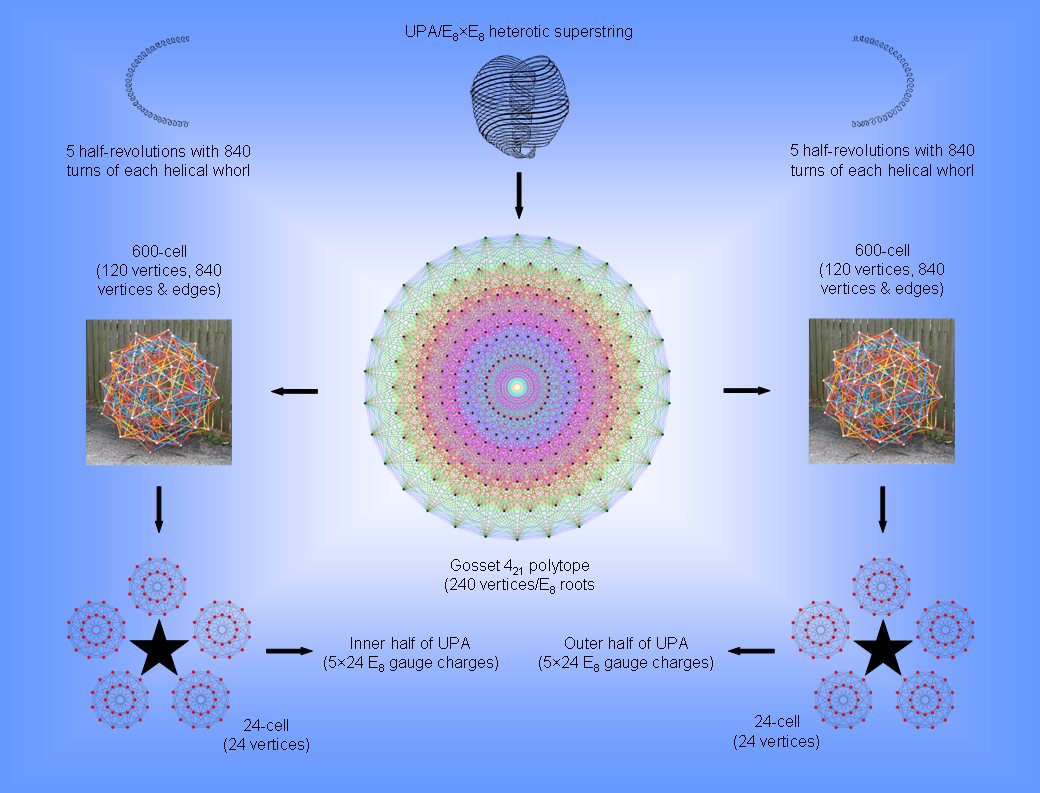
Figure 6. The connection between the UPA/superstring, the
421 polytope and 4-polytopes.
The compound of two 600-cells that is the
4-dimensional projection of the 421 polytope is the 4-dimensional manifestation of this archetypal
pattern exhibited by sacred geometries. Constructed from Type A triangles, it contains 4080 points,
where
4080 = (24 + 25 +
26 + 27) + (28 + 29 + 210 +
211),
240 = 24 + 25 + 26 + 27
is the number of vertices of the two 600-cells and
3840 = 28 + 29 + 210 + 211
is the number of other corners of their triangles. The two 600-cells have 13200 sides of 11520
triangles, i.e., 11760 sides other than their 1440 edges, where 11760 = 1680×7. This is the number of turns
in the seven helical minor whorls of the UPA. Each cell has 5760 triangles with 6600 sides, where 5760 =
(1+2+3+4)12×22×32×42 and 6600 = 55×120. The number 55 is the
sum of the first 10 integers and 120 is the sum of the first 10 odd integers after 1, showing how the Decad
determines the number of straight lines constructing the 600-cell. The Decad also determines its number of edges
because 720 yods surround the centre of a decagon with 2nd-order tetractyses as its sectors (see Fig. 9).
The 10×24 pattern characteristic of sacred geometries manifests in the subatomic world in the E8×E8 heterotic superstring
as the 120 E8 gauge charges that are
spread along the inner and the outer halves of the 10 whorls of the UPA, 12 charges per half-whorl (Fig.
6). The composition of each 600-cell representing the E8 charges carried by
the inner or outer half of the UPA in terms of five 24-cells determines the five half-revolutions of
each half. As 16800 = 240×70, it means that each E8 gauge charge manifests
as 70 turns of a helical whorl. This is both the number of yods in the Tree of Life created from tetractyses and
the number of corners of the (7+7) enfolded polygons of its inner form. As might be expected, each charge is a
whole in itself and so must be represented by a Tree of Life whose 16 tetractyses are composed of 70 yods. The
boundary of the 24-cell is composed of 24 octahedral cells with six meeting at each vertex, and three at each
edge. Together they have 96 triangular faces, 96 edges, and 24 vertices. The vertex-first parallel projection of
the 24-cell into 3‑dimensional space has a rhombic dodecahedral envelope. Twelve of the 24 octahedral cells
project in pairs onto six square dipyramids that meet at the centre of the rhombic dodecahedron. The remaining
12 octahedral cells project onto the 12 rhombic faces of the rhombic dodecahedron.
The superstring structural parameter 1680 and
its connection to the 240 roots/gauge charges of E8 manifest in another context. The sphere in 3-dimensional space
R3 has a 2-dimensional surface S2. In (n+1)-dimensional space Rn+1,
the n-sphere Sn with radius r is the set of points
{x1,x2,…xn+1} equidistant from a point
{c1,c2,…cn+1} such that
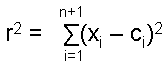
A question that has occupied mathematicians for
many years is: how many n-spheres can be packed in Rn+1 so as to touch a
central n-sphere? This is called the “kissing number problem,” the number K(n) being called the “kissing
number.” In 1-dimensional space, the 0-sphere is a point and the answer is 2 because a point at the middle of a
finite straight line is equidistant from the two points ends of this line. In 2-dimensional space, the 1-sphere
is a circle and six similar circles can be arranged at the corners of a hexagon so as to touch a circle of the
same radius at its centre. In 3-dimensional space, K(3) = 12, although it took until 1953 to prove this
rigorously. In 4-dimensional space, K(4) = 24 (first proved in 2003 by Oleg Musin). The densest lattice packing
of spheres in this space is for 24 3-spheres centred on the vertices of a 24-cell. It explains why the 600-cell
with 120 vertices can be regarded as five disjoint 24-cells. The problem is still unsolved for general n>4,
although various upper and lower limits for K(n) have been derived for certain value of n. However, the kissing
number problem is exactly solvable for spheres in eight and 24 dimensions. It was first proved in 1979 that K(8)
= 240. Amazingly, the number of 7-spheres that can touch a central sphere in 8-dimensional space is the same as
the number of vectors of the 8-dimensional root lattice space of E8! Not
only that, their centres coincide with the 240 lattice points! A point in 8-dimensional space has the
spherical coordinates (r, φ1, φ2, φ3, φ4, φ5, φ6, φ7). The positions of
points on 240 7-spheres require (240×7=1680) angular coordinates to specify them. This is the number of
1st-order spirillae in a whorl of the UPA that Leadbeater painstakingly counted 135 times [4]. It is yet
another way in which this superstring structural parameter appears in the group mathematics of
E8×E8 heterotic
superstrings.
Of course, the author does not claim that this
property (or, indeed, the properties of the 421 polytope as the convex hull of two 600-cells
discussed earlier) is the explanation of the string winding number
1680. This because the number refers to a property of spheres packed in a special, 8‑dimensional lattice, whereas
in the context of the UPA, it refers to the number of times a closed curve (whorl) winds around a 2-torus in
3-dimensional space. The crucial point is that it is highly unlikely that it could be just by chance that this number with a paranormal provenance appears naturally twice in a
narrow context connected to the group mathematics of superstrings, namely, the 421 polytope representing the root lattice of E8 as the convex hull of two 600-cells with 1680 vertices & edges and the 240
root vectors of E8 specified by 1680 angular coordinates. So any
criticism that all these mathematical facts on their own do not explain the 1680 turns in a helical whorl of
the UPA misses the point, for it is not being claimed here that these facts on their own do explain
them, merely that they are a visible component of the complete explanation to be provided by the as yet
undiscovered M-theory. The argument against coincidence has even more force vis-à-vis the UPA’s
structural parameters 840, 8400 & 16800, which we have seen manifest uniquely in this polytope. The
conclusion is inescapable that the UPA is a state of the E8×E8 heterotic superstring and
that both its space-time structure and the symmetry of its forces are laid out in the 4-dimensional sacred
geometries discussed in this section. The difference between all previous discussions of the embodiment of these
numbers and this one is that mathematicians have known for at least a century how the polychorons and the
421 polytope are related to the five exceptional Lie groups, the largest of which was established
thirty years ago by physicists Michael B. Green and John H. Schwarz as being relevant to one of the
five types of superstrings. What has now emerged is the existence of an undeniable connection between
these numbers of paranormal provenance and well-established facts in a branch of mathematics that is too
detailed to be dismissed as fortuitous.
The
Tetrad determines the superstring structural parameter 16800
According to Table 2, 14400 geometrical elements surround the centre of a 600-cell constructed from Type A
triangles. Two 600-cells contain 28800 geometrical elements surrounding their centres, where 28800 =
1!×2!×3!×4!(13+23+33+43). According to Table 3, their centres are
surrounded by 42000 yods, where 42000 = 1680×25. Noting that 168 = 132 − 1 = 3 + 5 + 7
+... + 25, i.e., it is the sum of the first 12 odd integers after 1, the superstring structural parameter 1680
is the sum of the 12 integers 30, 50, 70, ... 250 that can be assigned to the 12 yods on the boundary of a Type A
square, which has 25 yods, whilst 4200 is the sum of the same integer 1680 assigned to all its
yods:
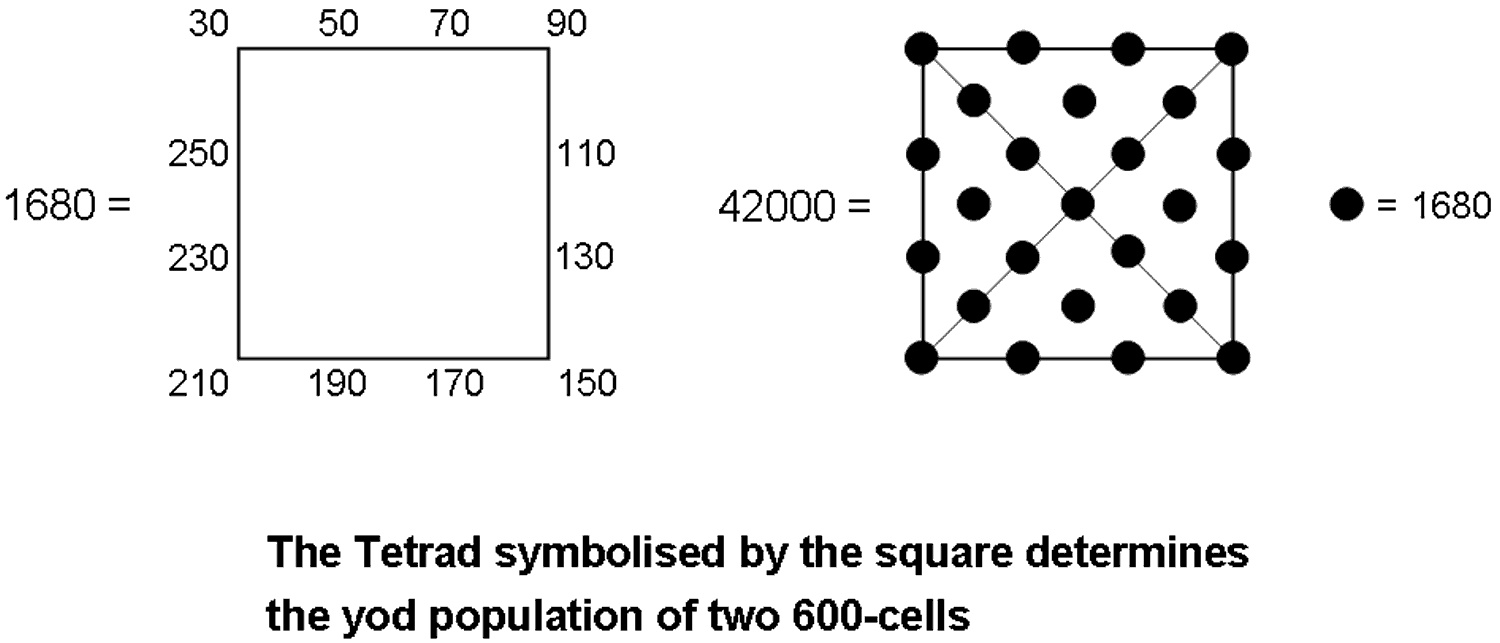
If the sceptic thinks that it is just
coincidence that the number of vertices & edges in two 600-cells should be the structural parameter of the
basic unit of matter that C.W. Leadbeater claimed to remote-view, despite their being connected to the
421 polytope representation of the roots of the symmetry group
E8 in E8×E8 heterotic superstring theory, then — to remain consistent —
he has to accept that it is also just a matter of chance that the square should simultaneously generate this
number and the yod population of the two 600-cells. How many such miraculous coincidences is he willing to accept
before he grudgingly admits that a profound, mathematical design embodied in the UPA is being revealed here? Any
argument based upon chance that he uses to justify his scepticism is untenable, given the degree of correlation
established in this article between the features of the UPA, the geometry of the two 600-cells as the 4-dimensional
projection of the 421 polytope and the five-fold distribution of their vertices
in 24-cells.
The Pythagorean integers 1, 2, 3 & 4
determine the 2400 faces of the two 600-cells because
| |
11
|
|
12
|
|
13
|
|
14
|
|
43
|
|
44
|
| |
21 21
|
|
22 22
|
|
23 23
|
|
24 24
|
|
33 33
|
|
34 34
|
|
2400 =
|
31 31 31
|
+
|
32 32 32
|
+
|
33 33 33
|
+
|
34 34 34
|
+
|
23 23 23
|
+
|
24 24 24
|
| |
41 41 41
41
|
|
42 42 42
42
|
|
43 43 43
43
|
|
44 44 44
44
|
|
13 13 13
13
|
|
14 14 14
14
|
They determine the number 1680 because
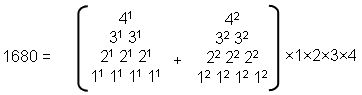
They determine the number 16800 because
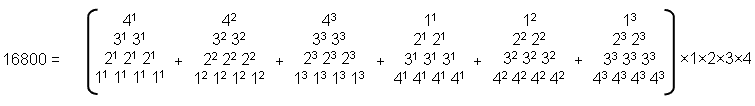
The
holistic 72:168 division in the two 600-cells making up the 240 vertices of the 421
polytope
As additional evidence of the holistic nature of the compound of two 600-cells, it will
be next proved that the yod composition of their faces displays the 72:168
division characteristic of holistic systems (see The holistic pattern).
Table 3 indicates that the 1200 faces of the
600-cell contains 13560 yods. Its 720 edges comprise (120 + 2×720 = 1560) yods. (13560−1560=12000) new
yods are needed to turn the faces into Type A triangles. Of these, 3600 hexagonal yods are at the centres of
the (3×1200=3600) tetractyses, leaving 8400 new yods on their sides. Therefore, 12000 = 3600 + 8400.
(2×12000=24000) new yods are needed to construct the 2400 faces of the two 600-cells. They contain (2×3600=7200)
hexagonal yods at the centres of the 7200 tetractyses and (2×8400=16800) new yods on their sides. Hence:
24000 = 7200 + 16800.
Ignoring the Pythagorean double factor of
100 originating from the fact that the two 600-cells have 2400 (=24×100) faces, we see that the pair of two
600-cells exhibits the 72:168 division that is found in all other sacred
geometries. Moreover, the 36:84 division differentiating (apart from a factor of 100) between
central hexagonal yods and boundary yods is exactly the same as the division of the 120 yods on the boundaries of
each separate set of seven enfolded polygons into 36 corners and 84 hexagonal yods (Fig.
7).
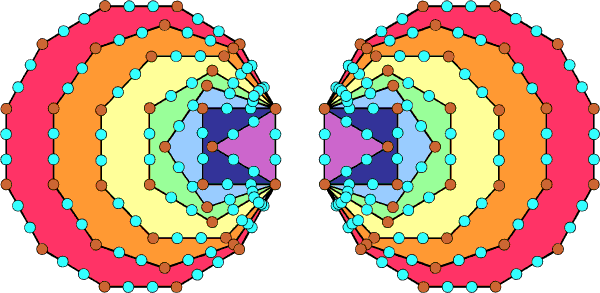 |
Figure 7. The 120 yods lining the sides of each set of 7
enfolded polygons consist of 36 brown yods at their corners
and 84 turquoise hexagonal yods. |
Article 62 discusses how other sacred geometries manifest this pattern in the
holistic parameter 240. The fact that it is revealed in the very pair of two 600-cells that
generates the 421 polytope when they are constructed from tetractyses is truly remarkable
evidence of the archetypal nature of this polytope as sacred geometry. In terms of the 240 roots of
E8, this division is between the 72 roots of its exceptional subgroup
E6 and its 168 remaining roots. Here is the sacred geometrical counterpart
of this property.
The holistic 192:192 division in the two
600-cells
We found in (2) above that the centre of a 600-cell is surrounded by 1920 corners of sectors in its 1200 faces and
720 interior triangles that are not vertices. Therefore, (192+192=384)×10 points other than vertices surround the
common centre of two 600-cells. As
| |
|
12 |
|
|
| |
|
22 |
32 |
|
| 385 = |
42 |
52 |
62 |
|
| |
72 |
82 |
92 |
102 , |
384 is the sum of the squares of 2-10, so that 1920 = 5×(22 +
32 + ... + 102). This means that the sum of the 90 squares of 2-10 arranged in a 10-fold
array surrounding the central square of 1 (Fig. 8) is 3840 — the number of corners other than vertices of the 7200
sectors of the 2400 faces of two 600-cells. This demonstrates the remarkable way in which the Decad determines the
number of points other than vertices that surround the common centre of the two 600-cells.
|

|
Figure 8. Each pentagram array of the squares 22-102 sums to 1920. This is the number of
corners of triangles in each 600-cell that are not its vertices or,
alternatively, the number of its external and internal
triangles when both types are simple triangles. |
Alternatively, if the 120 vertices of the 600-cell are joined to its centre, creating the sides
of triangles, and the internal triangles and the faces treated as simple triangles, then there are (1200+720=1920)
triangles and 1920 lines & triangles in its faces. It has (120+720=840) internal sides & triangles, as well
as (720+120=840) external & internal lines and (120+720=840) points & lines in its faces. So there are
three possible sets of 840 geometrical elements:
Assuming that their sets of 840 elements are compounded in the same way, the two 600-cells
sharing the same centre are composed of four possible sets of 1680 geometrical elements:
-
(840+840) points & lines in their 2400 faces;
-
(840+840) external & internal lines;
-
(840+840) internal lines & triangles;
-
(840+840) points & triangles.
Given that the compound of two 600-cells is composed of 1680 geometrical elements in four
different ways, there can be no doubt whatsoever that it embodies the paranormally obtained superstring structural
parameter 1680! It does not need its construction from Type A triangles to demonstrate that — its own,
unreconstructed geometry suffices. But the latter is required to show that the compound embodies the
numbers 8400 and 16800 as well. Notice that even a single 600-cell can embody the number 1680, for
its faces are composed of 840 points & lines, whilst its interior has 840 lines & triangles. Alternatively,
it has 840 lines and 840 points & internal triangles. The question now arises: which of all these possibilities
is the correct geometrical analogue of the 1680 turns in a helical whorl of the UPA? To answer this question, it
must be pointed out that, whilst necessary, it is not sufficient that a parameter of holistic systems be embodied
in a geometry for the latter to count as sacred. True parameters of holistic systems are not isolated; they are
also interconnected, forming mathematical patterns that are always the same from one holistic system to another.
Study of these systems has shown that one such pattern is the sum:
192 = 24 + 168
(or a pattern with 10 times these numbers). A holistic parameter may be present in a sacred
geometry in more than one way. Its "correct" way will be that which is consistent with the holistic patterns that
the geometry displays. In the case of the 600-cell constructed from simple triangles, there are (720+1200=1920)
lines & triangles in its faces and (720+1200=1920) triangles in its faces and interior. In neither case,
however, does this number include the number 240. This appears only as the sum of the 120 vertices and the 120
internal lines, but in each case the number 120 is also part of the number 840 instead of being separate from it,
which it needs to be in order to create the sum: 1920 = 240 + 1680. This holistic pattern only manifests in the
pair of 600-cells, which contains 240 points (vertices) and 1680 lines (edges & internal lines),
i.e., 1920 points & lines. As we have found that sacred geometries embody the numbers 384 and 192 (or 10 times
these numbers) as:
384 = 192 + 192,
(see The holistic pattern and #19, #49, #58 & #59 in Wonders of correspondences), it indicates that the
truly complete, holistic system exhibiting the division: 3840 = 1920 + 1920 is one in which the compound is
replicated, i.e., there should be two 421 polytopes, each with 240 vertices
determining the 240 roots of E8. But this is, precisely, the
E8×E8 heterotic superstring theory, which this website demonstrates is encoded in the
inner Tree of Life, the five Platonic solids and the disdyakis triacontahedron! Hence, this particular
superstring theory is the simple consequence of holistic systems having two suitably defined "halves", each
embodying the number 192 (or 1920). The correct way of seeing how the superstring structural parameter 1680 is
embodied in either the 600-cell or two 600-cells composed of simple triangles is the one that is consistent with
both the sums: 1920 = 240 + 1680 and 1680 = 840 + 840. The only one that is consistent with them
is a compound of two 600-cells with 240 points, 1680 lines and 1920 points & lines, i.e., each
600-cell with 840 sides of external and internal simple triangles represents half a helical whorl
with 840 turns. This is consistent with the conclusion reached in Article 62 that, in terms of its vertices, the two 600-cells composed of Type A
triangles represent the outer and inner halves of a UPA/E8×E8 heterotic superstring,
the 120 vertices in each denoting 120 E8 roots/gauge charges that are spread along either half,
whilst each of the five half-revolutions of the 10 whorls in each half is represented by one of the five
disjoint 24-cells that make up a 600-cell. The division: 840 = 120 +720 observed for the sides of exterior and
interior triangles in each 600-cell is the exact counterpart of what is found in the inner &
outer Trees of Life, where 120 yods making up half of the 1-tree constructed from Type A triangles can be
associated with the 720 yods that surround the centres of each set of seven separate Type B polygons (see Fig. 7
in #1 of this section). That the superstring divides into an inner and
an outer half due to this 120:120 division of vertices/E8 gauge charges is confirmed by the fact
that, when the faces and interior triangles of each 600-cell are Type A triangles instead of simple triangles,
(7×1200=8400) geometrical elements are added in the 1200 faces of each 600-cell. In other words, these elements
are the counterpart of the 8400 helical turns in the outer or inner halves of the UPA.
The Decad determines 120, 1200, 720 &
840
The ancient Pythagoreans regarded 2 as the first true integer because they taught that the number 1 (the Monad) was
not a number but the source of all numbers, including integers. They would have treated the number
11, the tenth integer after 1, as the tenth true integer and 3 as the first true odd integer. As
112 − 1 = 121 − 1 = 120 = 3 + 5 + 7 +... + 21, the Decad determines the 120
vertices of the 600-cell arithmetically as the sum of the first 10 odd integers. It also determines this number in
a geometrical way because the centre of a Type B dodecagon is surrounded by 120 points, lines & triangles and
the dodecagon is the 10th type of regular polygon. The Decad determines its 1200 faces because 1200 = 10×120 =
10(3+5+7+... +21) = 30 + 50 + 70 +...+210. The tenth prime number is 29. As
292 − 1 = 840 = 3 + 5 + 7 +... + 57, the number 840 is the sum of the first 28 odd integers after
1. Therefore,
840 − 120 = 720 = 23 + 25 + 27 +... + 57,
i.e., 720 is the sum of 18 odd integers. The Decad determines arithmetically both the number of
vertices in the 600-cell and its 840 vertices & edges. It determines the 720 edges as well because there are
720 yods surrounding the centre of a decagon whose sectors are 2nd-order tetractyses (Fig. 9).
|
|
Figure 9. 720 yods surround the centre of a decagon whose
sectors are 2nd-order tetractyses. |
|

UPA
|
|

whorl
|
The UPA is a set of 10 closed curves, or "whorls."
Each whorl is a closed helix with 1680 circular turns.
Each whorl winds 5 times around the axis of spin.
The 10 whorls make 50 revolutions around this axis.
Each whorl has 168 turns in a half-revolution.
Each whorl has 336 turns in one revolution.
The 10 whorls have 3360 turns in one revolution.
The 10 whorls have 1680 turns in a half-revolution.
The inner half of each whorl winds 2½ times around axis.
The 10 whorls have 8400 turns in inner/outer half of UPA.
Each whorl has 840 turns in inner/outer half of UPA
|
|

3-d projection of the rotating
600-cell.
|

3-d projection of the rotating
600-cell.
|
|
120 vertices→120 roots of
E8.
(120+720=840) sides of (1200+720=1920) triangles.
1680 hexagonal yods line the sides of the 1920 tetractyses.
|
120 vertices→120 roots of
E8.
(120+720=840) sides of (1200+720=1920) triangles.
1680 hexagonal yods line the sides of the 1920 tetractyses.
|
.png) |
.png) |
The holistic 168:168 division in the two
600-cells
When the 600-cell is composed of simple tetractyses, (720×2=1440) hexagonal yods line
sides of the 1200 tetractyses in its faces and (120×2=240) hexagonal yods line the 120 internal sides of the 720
tetractyses in its interior. Therefore, (1440+240=1680) hexagonal yods line the (720+120=840) sides of its
(1200+720=1920) tetractyses. The superstring structural parameter 1680 recorded by C.W.
Leadbeater when he remote-viewed the UPA is the number of hexagonal yods in a single 600-cell that correspond (in
terms of the formal correspondence between yods and Sephiroth) to the six Sephiroth of Construction above
Malkuth. Here is yet more confirmation of the superstring nature of the UPA. The pair of 600-cells has
(1680+1680=3360) hexagonal yods on the 1680 sides of their (1920+1920=3840) tetractyses. This is the number of
turns in one revolution of the 10 whorls. Once again, we see that each 600-cell is representing all 10 whorls, but
this time a half-revolution of them instead of five half-revolutions. See The holistic pattern for examples of sacred geometries displaying the
168:168 or 1680:1680 divisions. The remarkable ways in which polygonal
numbers and sacred geometries represent the superstring structural parameter 3360 (number of turns in one
revolution of the 10 whorls of the UPA) are shown here. Notice, finally, how the pair of 600-cells manifests the
192:192 division of the holistic parameter 384 as the 1920 tetractyses in each 600-cell.
The holistic 120:720 division in the two 600-cells
and in sacred geometries
Figure 7 in #1 displays how the number 1680 is embodied in 1. the disdyakis
triacontahedron, 2. the 1-tree & the two sets of 7 separate Type B polygons, and 3. the first four Platonic
solids. Their geometrical or yod compositions conform to the pattern:
1680 = 720 + 240 + 720.
This pattern manifests in a single 600-cell composed of simple triangles as the 720 edges,
(120+120=240) vertices & internal sides and 720 internal triangles. It appears in two 600-cells as their 240
vertices and their pair of 720 edges. Let us examine these sacred geometries in more detail in order to demonstrate
how the holistic 120:720 division exhibited by the 600-cell in both its faces and its interior and by two 600-cells
in their vertices & edges manifests in each half of these sacred geometries.
Disdyakis triacontahedron
The polyhedron has 62 vertices, 180 edges & 120 triangular faces. Surrounding an axis
passing through two diametrically opposite vertices are 360 (=36×10) geometrical elements
comprising 60 vertices, 180 edges, i.e., 240 vertices & edges, and 120 triangles. Joining its vertices to its
centre creates internal triangles which, when Type A, are composed of 180 points, (60 + 3×180 = 600) lines &
(3×180=540) triangles surrounding the axis. Hence, (60+180=240) points, (180+600=780) lines & (120+540=660)
triangles surround the axis. Each half of the disdyakis triacontahedron is composed of 120 points, 390 lines &
330 triangles. i.e., 120 points and 720 lines & triangles. Therefore, the 1680 geometrical elements surrounding
the axis consist of two sets of elements, each comprising 840 elements made up of 120 points and 720 lines &
triangles. Each half of the disdyakis triacontahedron is the 3-dimensional analogue of a 600-cell with 120 vertices
& 720 edges.
Outer & inner form of 1-tree
Constructed from 19 Type A triangles, the
1-tree contains 251 yods. Of these, 11 are corners of triangles that coincide with Sephiroth, leaving 240 yods
generated by this transformation. The seven regular polygons making up each half of its inner form contain 727 yods
when they are Type B. 720 yods surround their centres. It was shown here that the 240 yods in the 1-tree consist of 10 sets of 24
yods. Yods in triangles that are on the left or the right of the central Pillar of Equilibrium can be associated
with the yods in the seven regular polygons on that side. The yods that line this pillar as the axis of symmetry
of the 1-tree can be divided into two sets containing the same number. Of course, unlike the yods in each set of
polygons, these central yods are not mirror images of each other. However, one set can be associated with the
left-hand set of polygons and the other set associated with the right-hand set. This means that 120 yods in the
1-tree can be associated with each set of polygons. The 1680 yods can be divided into two sets of (120+720)
yods.
When the interior triangles of a 600-cell formed by joining its centre to
its vertices are simple triangles, it has (1200+720=1920) triangles with (120+720=840) sides. The compound of two
600-cells has (1920+1920=3840) triangles with (840+840=1680) sides. This shows how the pair of 600-cells embodies
the superstring structural parameter 1680, the 840 sides of the 1920 triangles in each 600-cell corresponding to
the 840 turns in an outer or inner half of the UPA/superstring. The same 120:720 division appears in the inner form
of 10 overlapping Trees of Life whose (70+70) enfolded Type B polygons are divided into their
sectors:

|
The 3n
triangles in a Type B n-gon have (2n+1) corners. The 36 triangles
in a Type B dodecagon (n=12) have 25 corners, of which 13 are corners of its 12 sectors/Type A
triangles. 12 corners are associated with each dodecagon. Noting that the triangle occupies one
of the sectors of the hexagon, a corner of the triangle coincides with the centre of the hexagon
and that a corner of a pentagon coincides with the centre of the decagon, the number of corners
in the (47×3=141) triangles making up the 47 sectors of the 7 enfolded Type B polygons = ∑(2n+1)
− 6×2 − 1 − 1 − 1 = 2×48+ 7 − 12 − 3 =
88. Three of these coincide with Sephirothic corners of triangles in the outer Tree of Life,
leaving 85 intrinsic corners, where
85 =
40+ 41+
42+
43.
Of these, 84
are associated with each set of 7 enfolded polygons. The (7+7) enfolded Type B polygons have
(84+84=168) corners of 282 triangles that are unshared with the outer Tree,
where 282 is
the number value of Aralim, the
Order of Angels assigned to Binah. The 84 corners consist of the 12 corners of the 12 sectors
associated with the dodecagon, leaving 72 corners. Associated with the 1410 triangles in each set of 70 Type B
polygons enfolded in 10 overlapping Trees of Life are 840 intrinsic corners. They consist of
the 120 corners of the sectors of the 10 dodecagons and 720 other corners. This is how the
120:720 division characteristic of sacred geometries manifests in the inner form of 10 Trees
of Life. Both sets of polygons enfolded in 10 Trees have 2820 triangles with 1680 corners
unshared with these Trees:
1680 = 120 +
720 + 120 + 720 = 240 + 1440.
Each half of
the inner form of 10 Trees has 840 corners. They correspond to the 840 turns in an outer or
inner half of a whorl of the UPA/superstring, whose 10 space-time dimensions are represented by
10 Trees. Alternatively, each Tree represents a whorl (or, rather, one of its 10
half-revolutions) and the 10 Trees map the half-revolution of all 10 whorls of the
UPA.
Correspondence with the compound of two 600-cells
|
70 Type B polygons enfolded in 10 Trees of Life
|
|
600-cell
|
| 120 corners
associated with 120 sectors of the 10 dodecagons; |
→ |
120 vertices/sides of internal
triangles; |
| 720 intrinsic corners of triangles in 70
polygons; |
→ |
720 edges; |
| 840 intrinsic corners associated with
1410 triangles in 70 polygons; |
→ |
840 vertices & edges (or 840 sides of
1920 triangles); |
| 24 corners associated with dodecagons
enfolded in 2 Trees; |
→ |
24 vertices of 24-cell; |
| 120 corners associated with 5 pairs of
dodecagons enfolded in 10 Trees; |
→ |
120 vertices of compound of 5
24-cells. |
 |
600-cell
|

600-cell
|
| Each of the 10 whorls of the UPA twists 5
times around its axis of spin,
2½ times in its outer half and
2½ times in its inner half. Each half of a
helical whorl has 840 circular turns. |
Each member of the compound of two
600-cells that is the Coxeter plane projection of the 421 polytope has 840
vertices & edges (or sides of external and internal triangles). Their
superstring manifestation is the 840 turns in the outer or inner halves of each
whorl of the UPA/E8×E8 heterotic
superstring. |
|
First four Platonic solids
How the tetrahedron, octahedron, cube &
icosahedron embody the number 1680 is calculated here. When their faces and interiors are constructed from Type A
triangles, the numbers of corners, sides & triangles that surround their axes passing through two opposite
vertices are tabulated below in Table 2:
Table 2. Geometrical elements surrounding the axes
of the Platonic solids.
| Platonic solid |
Corners |
Sides |
Triangles |
Total |
| Tetrahedron |
24 |
78 |
66 |
168 |
| Octahedron |
48 |
156 |
132 |
336 |
| Cube |
48 |
156 |
132 |
336 |
| Icosahedron |
120 |
390 |
330 |
840 |
| Subtotal = |
240 |
780 |
660 |
1680 |
| Dodecahedron |
120 |
390 |
330 |
840 |
| Total = |
360 |
1170 |
990 |
2520 |
The 1680 geometrical elements surrounding the axes of the first four Platonic solids comprise
240 corners and 1440 sides & triangles. Surrounding the axes of the first three Platonic solids are 120 corners
and 720 sides & triangles, i.e., 840 geometrical elements. Similarly, 120 corners and 720 sides &
triangles, i.e., 840 geometrical elements, surround the axis of the icosahedron. Amazingly, the first three regular
3-polytopes and the icosahedron display the same 120:720 division as the 600-cell, which is the
4-dimensional counterpart of the icosahedron, the fourth Platonic solid! The compound of two
600-cells is the four-dimensional counterpart of the first four Platonic solids, their (120+120=240) vertices
corresponding to the (120+120) corners of triangles that surround the axes of the (first three+fourth) Platonic
solids. Together with the disdyakis triacontahedron, they are the 3-dimensional and 4-dimensional blueprints for
the E8×E8 heterotic superstring, which was paranormally described by Besant &
Leadbeater over a century ago. The same pattern is displayed by the icosahedron and the dodecahedron because the
latter is the dual of the former and has the same geometrical composition. This is not repeated in their
4-dimensional counterparts because the 120-cell (the 4-dimensional counterpart of the dodecahedron) has 600
vertices, not 120 vertices. It is, however, repeated for its 120 dodecahedra and 720 pentagonal faces. Just as the
disdyakis triacontahedron is generated from the rhombic triacontahedron as a compound of the icosahedron and
dodecahedron, so the 4-dimensional projection of the 240 vertices of the 421 polytope is the
compound of two 600-cells. In this sense, it can be regarded as analogous to the disdyakis triacontahedron — a
3-polytope. What is crucial to recognize is that the highly mathematical, hyper-dimensional objects that are being
discovered to underpin E8×E8 superstring physics have their
exact parallels in the sacred geometries of mystical traditions and ancient philosophies. Why?
Because they represent the same thing: the divine paradigm.
How the Godnames mathematically prescribe the 600-cell and
the pair of two 600-cells
Kether: EHIEH = 21
The first six rows in Pascal's triangle that contain binary coefficients other than 1 comprise
21 such numbers that add up to 240. This is the number of vertices in the two
600-cells:
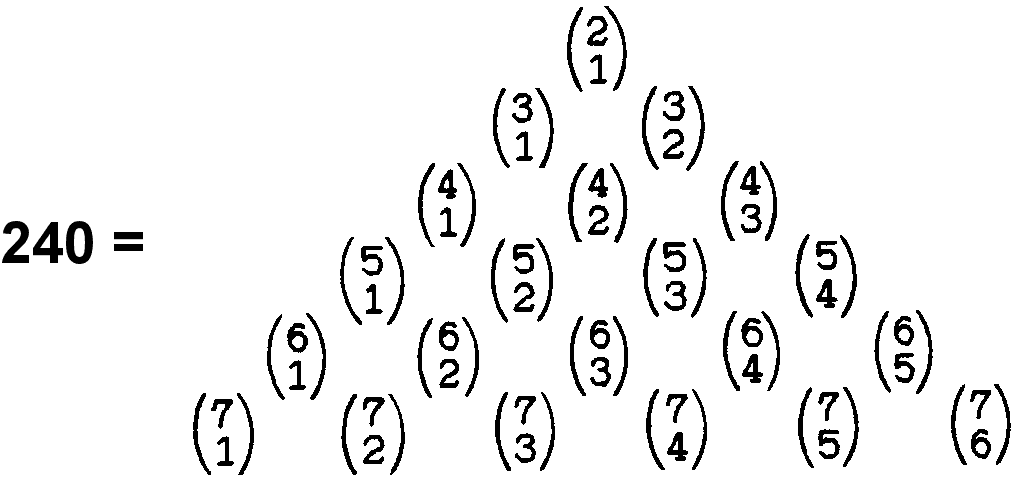
The centre of the 600-cell constructed from Type A triangles is surrounded by 21000
(=21×10×10×10) yods (see Table 3 on #1).
Chokmah: YAH = 15
The sum of the first
15 positive integers is 120, i.e., it is the 15th triangular number. This is
the number of vertices in the 600-cell. The sum of the first 15 even integers is 240, which
is the number of vertices in the two 600-cells. The two 600-cells have 1680 vertices & edges. The
sum of the 15 combinations of the four integers 21, 42, 63
& 84 (21 units apart) = 1680. The 15th prime number is 41,
where 412 − 1 = 1680.
Binah: ELOHIM = 50
2040 corners of 5760 triangles surround the centre of the 600-cell. Each half has 2880 triangles with 1020
(=102×10) corners. 102 is the 50th even integer after 2. ELOHIM prescribes the
form of the 600-cell by determining the number of the corners of its component triangles.
Chesed: EL = 31
The two 600-cells have 1680 vertices & edges.
1680 is the sum of the 31 combinations of the five integers 7, 14, 21, 28 & 35,
which are 7 units apart. Construction of the faces of the 600-cell from Type A triangles adds (7×1200=8400)
geometrical elements. The number 8400 is the arithmetic mean of
the 31 square numbers 52, 102,
152… 155.2
Geburah: ELOHA = 36
The 1200 faces of the 600-cell have 3600 (=36×10×10) sectors. It has 720 edges, where 720 =
72×10 and 72 is the 36th even integer.
Tiphareth: YAHWEH ELOHIM = 76
The pair of 600-cells composed of simple triangles has (1200+1200=2400) triangles in its faces and (720+720=1440)
internal triangles, making a total of 3840 (=384×10) triangles. 384 is the 383rd integer after 1, where 383 is the
76th prime number.
Netzach: YAHWEH SABAOTH = 129
Construction of the 2400 faces of two 600-cells from Type B triangles adds 16800 geometrical elements. As
168 = 132 − 1,
16800 = 168×102 = (132 − 1)102 = 1302
−102 = (2×65)2 − (2×5)2
= 4(652 − 52).
652 = 1 + 3 + 5 + 7 + 9... +
129
and
52 = 1 + 3 + 5 + 7 + 9.
Therefore,
16800 = 4(11 + 13 + 15 +... + 129).
The number 16800 is the sum of (4×60=240) odd integers, the smallest of which is 11, the 10th
integer after 1, and the largest of which is 129, the 65th odd integer, where
65 is the sum of the first 10 integers after 1.
Hod: ELOHIM SABAOTH = 153
1560 (=156×10) yods line the 720 edges of the 600-cell when constructed from tetractyses or Type A triangles. 156
is the 153rd integer after 3, the first odd integer.
Yesod: EL ChAI = 49
Inside the 600-cell are 2160 triangles with 2280 (=228×10) sides, where 228 is the 227th integer after 1 and 227 is
the 49th prime number. Two 600-cells have 2400 triangular faces. As
492 = 2401, 2400 = 492 − 1. This is the dimension
of SU(49).
Malkuth: ADONAI = 65
The 600-cell has (120+720=840) vertices & edges. As 120 = 5! and 720 = 6!, 840 = 6! + 5!. These two integers
make up the gematria number value of ADONAI. The 3600 triangular sectors of the 1200 faces of the 600-cell have
1320 (=132×10) corners, where 132 is the 65th even integer after 2. The 5760 triangles in its
faces and interior have 6600 (=66×10×10) sides, where 66 is the 65th integer after 1.
ADONAI MELEKH = 155
The number of yods lining the 720 edges connecting the 120 vertices of the 600-cell = 120 + 720×2 = 1560 (=156×10).
156 is the 155th integer after 1.
The sum of the Godname numbers of the first six Sephiroth of Construction is 240 — the number of
vertices of the 421 polytope denoting roots of E8, as well as the number of vertices of
the two 600-cells:
240 = 21 + 26 + 50 +
31 + 36 + 76.
The 240 vertices of the 421 polytope can be constructed in two sets:
112 (22×8C2) with coordinates obtained from (±2, ±2, 0, 0,
0, 0, 0, 0) by taking an arbitrary combination of signs and an arbitrary permutation of coordinates, and 128 roots
(27) with coordinates obtained from (±1, ±1, ±1, ±1, ±1, ±1, ±1, ±1) by taking an even number of minus
signs (or, equivalently, requiring that the sum of all the eight coordinates be even). The division 240 = 128 +
112 is reproduced in the sums of the Godname numbers of the first four Sephiroth in the set
of six:
128 = 21 + 26 + 50 +
31
and the last two Sephiroth:
112 = 36 + 76.
112 is the number value of Beni Elohim (the
"sons of God" referred to in biblical Genesis). Table 2 on #1 indicates that the same division manifests in the sides of the
triangles making up the 8-cell. Its 24 square faces have 40 corners (16 vertices & 24 corners) and 128 sides
(32 edges & 96 sides) of 96 triangular sectors, i.e., (40+128=168) corners & sides
(48 vertices & edges; 120 corners & sides). This is how the 8-cell embodies the
superstring structural parameter 168. Its 96 interior triangles have
112 sides. The (96+96=192) triangles have (128+112=240) sides.
Table 2 above shows that, when constructed from Type A triangles, there are 840 geometrical
elements surrounding the axis of the icosahedron. They comprise 120 corners and 390 sides of 330 triangles, i.e.,
720 sides & triangles. Compare this with its 4-dimensional counterpart: the 1200 faces of the 600-cell have 120
vertices & 720 edges, i.e., 840 vertices & edges. It is an example of how parameters of holistic systems
are related by the same patterns, in this case: 840 = 120 + 720. In fact, the same pattern appears in the
tetrahedron, octahedron & cube because, according to Table 2, 120 corners of 720 sides & triangles surround
their axes, so that the axes of the first four Platonic solids are surrounded by (120+120=240) corners of
(720+720=1440) sides & triangles. This is the 3-polytope analogue of the compound of two 600-cells, which have
(120+120=240) vertices and (720+720=1440) edges. The division: 840 = 120 +720 does exist in the
120-cell, the dual of the 600-cell, but as its 120 dodecahedral cells and 720 pentagonal faces. Whilst a pair of
120-cells has 240 dodecahedra and 1440 faces, i.e., 1680 faces & dodecahedra, this combination (unlike the pair
of 600-cells) has no geometrical connection to the 421 polytope. Instead, a single 120-cell
embodies the number 16800 as the number of geometrical elements other than centres of Type A faces and internal
triangles (see comment 1 on #1). As a 600-cell has 8400 geometrical elements within its Type A faces
and 8400 yods line the sectors of its faces other than those lining its edges, it requires two such polytopes to
generate the superstring structural parameter 16800. Only a pair of 600-cells can display simultaneously the
holistic parameters 240 and 16800. A single 120-cell displays the number 120 and the number 16800, whilst a pair
of them displays the numbers 240 and 33600. But the latter is not a structural parameter of a
single UPA. Instead, it is the number of turns in the whorls of two UPAs. So, even though it
displays the divisions: 240 = 120 + 120 and 840 = 120 + 720, a pair of 120-cells cannot be regarded as a
polytope model for the UPA because it does not embody the number 240 in a way that clearly refers to the 240
roots of E8 whose gauge charges are present in the E8×E8 heterotic
superstring.
The same patterns and superstring
structural parameters 840 & 1680 appear in both the first four Platonic solids and the compound of
600-cells whose 240 vertices are the 4-dimensional projection of the 240 vertices of the 421 polytope. This fact established in Article 62 is yet another argument against the possibility of these
paranormally-based numbers appearing by chance in the two centre-sharing 600-cells. It is also strong evidence
that they conform to the universal patterns exhibited by sacred geometries discussed in The holistic pattern. It implies that
the pair of 600-cells does, indeed, constitute sacred geometry. Given their mathematical connection to the
421 polytope, whose 240 vertices define the 240 root vectors of the Lie group E8
describing one of the two types of heterotic superstrings, the conclusion is inescapable that this type of
superstring exists. How can it not exist and yet its group mathematics be embodied in analogous ways in
the sacred geometries of some of the world's religions? Just a coincidence? How can it not exist and
yet purported paranormal description of the constituents of matter match exactly this geometrical embodiment in
both qualitative and quantitative ways? Just another coincidence? Whilst a sceptic might speculate that this
happened by chance or make accusations of cherry-picking if he were presented with only one example as alleged
evidence that superstrings exist, even he would have to admit that it is improbable in the extreme that his
facile explanation could apply as well to all the other sacred geometries discussed on this website that display
the same patterns and parameters. Unless he can provide a more plausible alternative (and, of course,
he cannot), his scepticism is indefensible, being based upon ideological prejudice rather than logical
argument.
Home









.png)






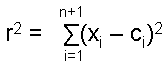

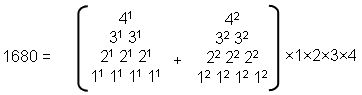
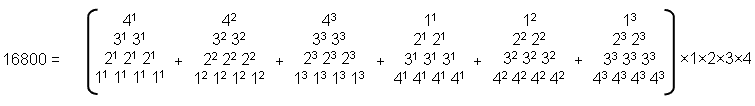






.png)