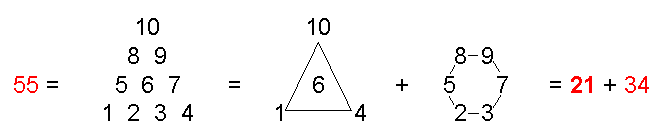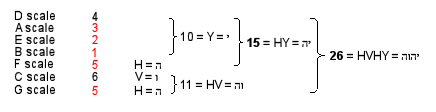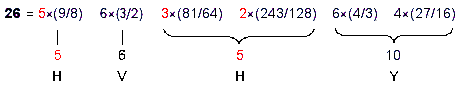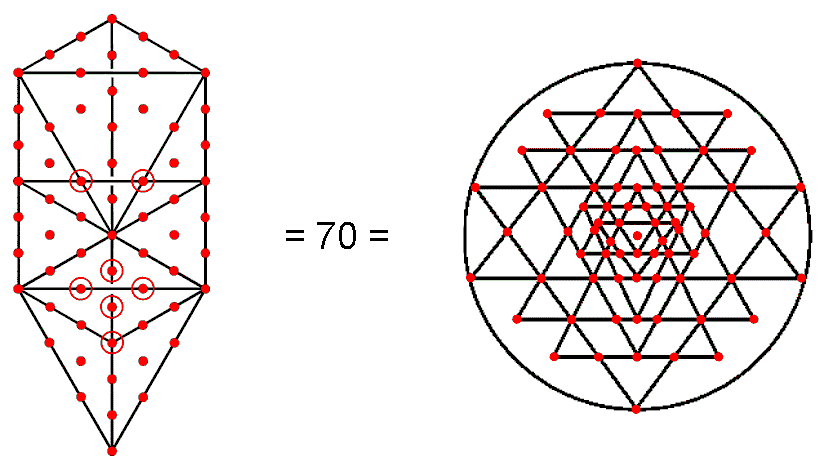Home
ARTICLE 51

by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth.
Dorset BH2 5PH. England.
Website: http://www.smphillips.mysite.com
Abstract
|
The first 55 notes above the
tonic of the Pythagorean musical scale comprise 26 overtones. This is
the gematria number value of Yahweh (YHVH), the well-known name of God.
The gematria number values of its letters are the numbers of overtones
in consecutive sets of notes whose numbers are Fibonacci numbers, 55
being the tenth of these numbers. The 21:34 division of notes determined
by YH and VH creates a 3:5 division of the eight octaves spanned by the
55 notes. Their counterparts in the 1-tree are the 21 geometrical
elements in its Lower Face and the 34 elements outside the latter. The
21:34 division appears in the inner form of the Tree of Life as the 21
corners of the triangle, octagon & decagon and the 34 corners of
sectors that are either centres of polygons or corners of the square,
pentagon, hexagon & dodecagon. This division manifests in the five
Platonic solids as the 21 vertices & centres of the tetrahedron,
octahedron & cube and as the 34 vertices & centres of the
icosahedron & dodecahedron. It also distinguishes the geometry of
the faces of the first four solids from that of the fifth solid. There
are 55 Sephirothic levels (SLs) on the central pillar of the 26-tree
mapping the 26-dimensional space-time predicted by quantum mechanics for
spinless strings. Their 21:34 division distinguishes the nine
superstring dimensions from the sixteen higher, bosonic string
dimensions. The same division distinguishes the three large-scale
dimensions from the six compactified dimensions. This means that
Fibonacci numbers, which pattern and give proportion to many living
things, also determine and divide the very dimensionality of
space-time. This division is reflected in the sacred geometries of the
Tree of Life and the five Platonic solids, providing evidence of a
universal blueprint that governs matter and life.
|
Introduction
Fibonacci numbers are members
of the infinite series of numbers:
5, 8,
13, 21,
34, 55, 89, 144, 233,
377…
in which, starting from the third number, each number is the sum of the
two previous ones. The ratio of two consecutive numbers converges towards the Golden
Ratio φ = 1.61803398… as they become larger and larger. They appear widely in
Nature.1 This article shows how they group notes in the Pythagorean
musical scale in a way that corresponds to the geometrical composition of the Tree of
Life and the five Platonic solids, as well as to the dimensionality of the space-time of
superstrings and bosonic strings.
1
|
Table 1. Gematria number values of the ten Sephiroth in the four Worlds.
|
|
SEPHIRAH
|
GODNAME
|
ARCHANGEL
|
ORDER OF ANGELS
|
MUNDANE CHAKRA
|
| 1 |
Kether
(Crown)
620 |
EHYEH
(I am)
21 |
Metatron
(Angel of the Presence)
314 |
Chaioth ha Qadesh
(Holy Living Creatures)
833
|
Rashith ha Gilgalim
First Swirlings.
(Primum Mobile)
636 |
| 2 |
Chokmah
(Wisdom)
73 |
YAHWEH, YAH
(The Lord)
26,
15
|
Raziel
(Herald of the Deity)
248 |
Auphanim
(Wheels)
187 |
Masloth
(The Sphere of the Zodiac)
140 |
| 3 |
Binah
(Understanding)
67 |
ELOHIM
(God in multiplicity)
50
|
Tzaphkiel
(Contemplation of God)
311
|
Aralim
(Thrones)
282
|
Shabathai
Rest.
(Saturn)
317 |
| |
Daath
(Knowledge)
474 |
|
|
|
|
| 4 |
Chesed
(Mercy)
72 |
EL
(God)
31 |
Tzadkiel
(Benevolence of God)
62 |
Chasmalim
(Shining Ones)
428
|
Tzadekh
Righteousness.
(Jupiter)
194 |
| 5 |
Geburah
(Severity)
216
|
ELOHA
(The Almighty)
36
|
Samael
(Severity of God)
131
|
Seraphim
(Fiery Serpents)
630
|
Madim
Vehement Strength.
(Mars)
95 |
| 6 |
Tiphareth
(Beauty)
1081
|
YAHWEH ELOHIM
(God the Creator)
76 |
Michael
(Like unto God)
101
|
Malachim
(Kings)
140
|
Shemesh
The Solar Light.
(Sun)
640 |
| 7 |
Netzach
(Victory)
148
|
YAHWEH SABAOTH
(Lord of Hosts)
129
|
Haniel
(Grace of God)
97 |
Tarshishim or Elohim
1260
|
Nogah
Glittering Splendour.
(Venus)
64 |
| 8 |
Hod
(Glory)
15
|
ELOHIM SABAOTH
(God of Hosts)
153
|
Raphael
(Divine Physician)
311
|
Beni Elohim
(Sons of God)
112
|
Kokab
The Stellar Light.
(Mercury)
48 |
| 9 |
Yesod
(Foundation)
80
|
SHADDAI EL CHAI
(Almighty Living God)
49,
363
|
Gabriel
(Strong Man of God)
246
|
Cherubim
(The Strong)
272
|
Levanah
The Lunar Flame.
(Moon)
87 |
| 10 |
Malkuth
(Kingdom)
496
|
ADONAI MELEKH
(The Lord and King)
65,
155
|
Sandalphon
(Manifest Messiah)
280 |
Ashim
(Souls of Fire)
351
|
Cholem Yesodoth
The Breaker of the Foundations.
The Elements.
(Earth)
168 |
|
The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah.
Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their
physical manifestation). This table gives their number values obtained by the ancient practice
of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving a
number value to a word that is the sum of the numbers of its letters.
|
(All numbers in this table referred to in the article are written in
boldface).
3
1. Fibonacci numbers in the Pythagorean musical
scale
Table 2 displays the first 55 notes in the Pythagorean musical scale above the tonic of the first octave (red
numbers are Fibonacci numbers):
Table 2. The first 55 notes above the tonic of the Pythagorean
scale.
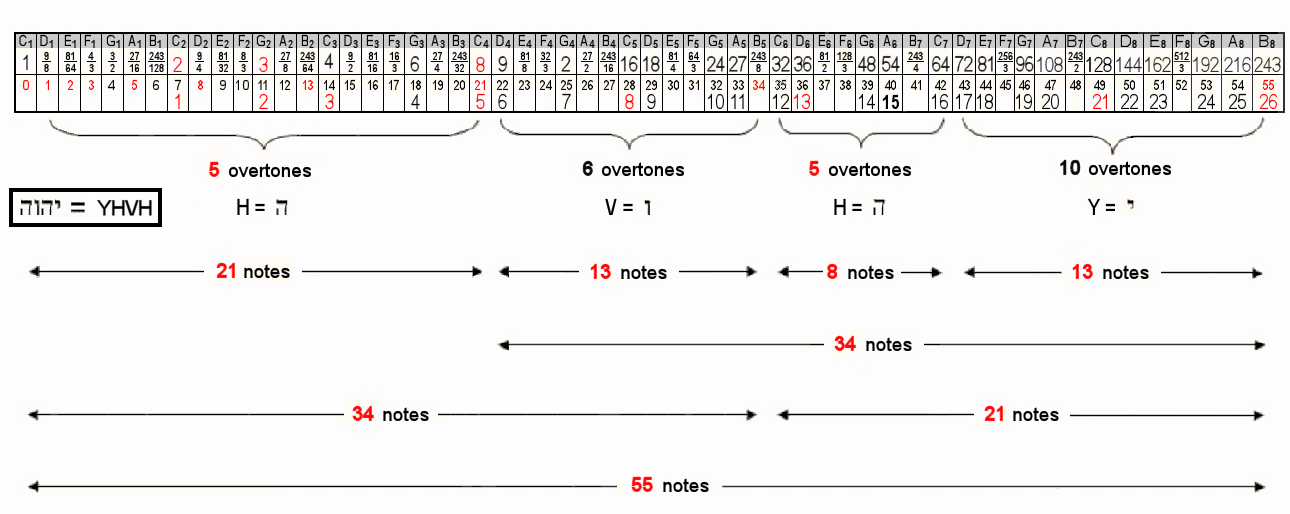
The first seven octaves of the Pythagorean scale ending in the note C8 with tone
ratio 27 = 128 comprise 50 notes, of which 21 notes are overtones and 29 are partials. ELOHIM, the Godname of Binah with
number value 50, and EHYEH, the Godname of Kether with number value 21, prescribe the first seven octaves. They comprise the tonic C1, the
last note C8 and the 48 notes between them. The latter consist of the six
octaves C2–C7 and 42 notes made of 14 overtones and 28 partials. The first
55 notes above the tonic ending with note B8 comprise
26 overtones and 29 partials. YAHWEH (Hebrew: YHVH), the Godname of Chokmah with number
value 26, prescribes this set of 55 notes. It consists of
the seven octaves C2–C8 and 48 notes made up of 19 overtones and
29 partials.
That this is not just a coincidence is indicated by the fact that the letter values of YHVH
denote the numbers of overtones in groups of notes whose numbers are Fibonacci numbers. H = 5 (he)
denotes the 5 overtones in the first 21 notes, V = 6 (vav) denotes the six overtones in the next 13 of the first 34 notes, H = 5 denotes the 5 overtones in the next 8 notes and Y = 10 (yod) denotes the
ten overtones in the last 13 notes. The letter values of YAHWEH divide up the
55 notes above the tonic into sets whose numbers are always members of the
Fibonacci series! YAH (Hebrew: YH), the partial version of the full Godname with number value
15 specifies the 15 overtones in the last 21 notes, the two letters Y and H denoting the subsets with, respectively,
13 notes and 8 notes. This division in the Godname
occurs at C6, the 5th octave with tone ratio 32. The first
5 overtones span 3 octaves, as do the next 11
overtones and the last 15 overtones. The 55 notes from
D1 with tone ratio 9/8 to B8 with tone ratio 243 span an interval of
216. This is the number value of Geburah. The interval between B8 and the next
note C9 is 256/243, which is the Pythagorean leimma. The ratio of the tone ratios of the
55th and 21st notes is 243/8,
which is that of the 34th note! The 21:34 division in the Fibonacci number 55 creates a
3:5 division of the 8 octaves spanned by the 55 notes. The numbers 3, 5 & 8 are themselves
consecutive Fibonacci numbers! Counting from the 55th note, the
21:34 division generates the
same 3:5
division. The first 32 notes have ten overtones. As 32 is
3
not a Fibonacci number, we see that only counting backwards from the 55th note generates the gematria numbers of the letters of YAHWEH in the order in which
they are written in Hebrew:
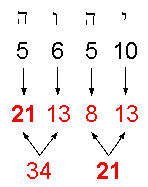
This is remarkable because it demonstrates that the pattern of overtones is prescribed by
this Godname not in the left-to-right way that it is written in English but in the right-to-left way
that it is written in its natural, Hebrew language!
2. Fibonacci numbers in the Tree of Life & 1-tree
The geometrical
compositions of the Tree of Life and 1-tree are shown below:
Points
Lines
Triangles
Total
Tree
of
Life:
10
22
16
48
1-tree: 11
25 19
55
The 48 geometrical elements comprising the Tree of Life correspond to the
48 corners of the seven separate polygons and to the 48 notes up to
B8 other than octaves. The extra seven geometrical elements (one point, 3 lines & 3 triangles) needed to convert the Tree of Life
into the 1-tree correspond in the inner Tree of Life to the centres of its seven regular polygons and in the
Pythagorean scale to the seven octaves up to the note B8.
Outer Tree of Life
As discussed in more detail in Article 50,2 the Lower Face of the Tree of Life is the red kite-shape in Figure 1 whose
corners are Tiphareth, Netzach, Hod, Yesod and Malkuth. It comprises 21 geometrical elements, where 21 is
the eighth Fibonacci number. This is the number of elements in the similarly-shaped Upper Face of the 1-tree
whose corners are Kether, Chokmah, Binah, Chesed, Geburah and Tiphareth. As the two Faces share a
corner, 20 of the elements in the Upper Face are part of the 34
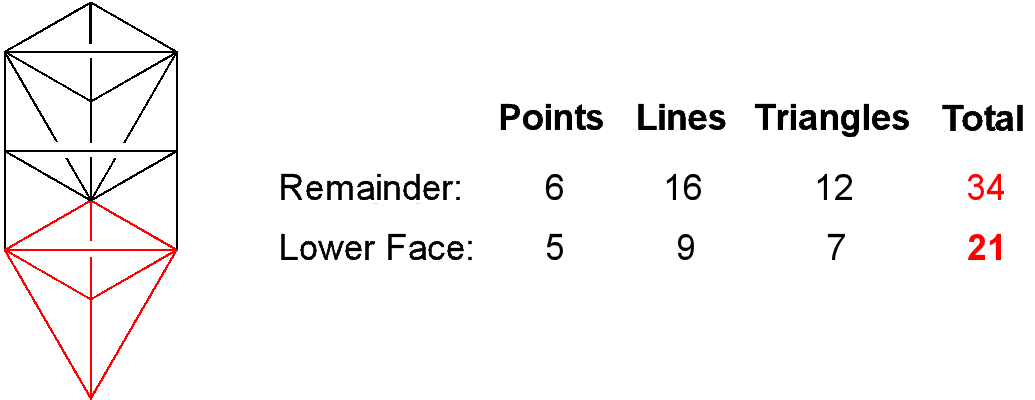
Figure 1. The 55 geometrical elements of
the 1-tree comprise the 21 elements of its Lower Face (red)
and the 34 elements in its remainder (black).
geometrical elements that make up the 1-tree other than its Lower Face, leaving
(34–20=14) elements outside both Faces. The 21:34 division of the 55 elements in the 1-tree has its counterpart in the tetractys array of the first ten
integers adding to 55 (notice that 55 is also
the tenth Fibonacci number):
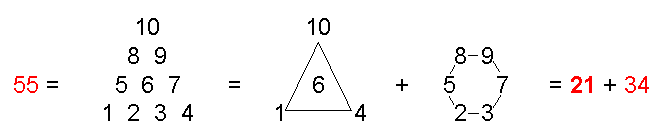
The sum of the integers at the corners and centre of the array is 21, and the sum of the integers at the corners of the hexagon is 34. 21 is the sum of the first six integers
1–6 and 34 is the sum of the last four.
Inner Tree of Life
The 48 sectors of the seven separate regular polygons have 55
corners (Fig. 2). They comprise the seven centres of the polygons and their 48
corners. Their musical counterparts in the first seven octaves are the seven octaves
C2–C8 and the 48 notes comprising 19 overtones and 29 partials. The
extra seven
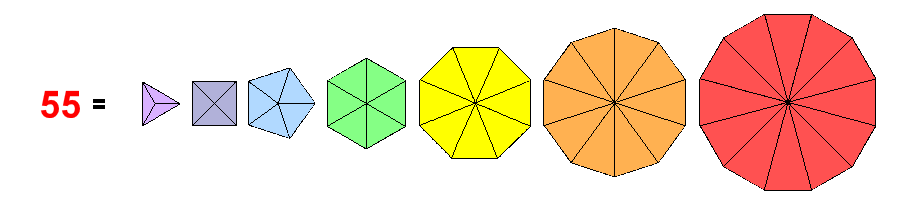
Figure 2. The tenth Fibonacci number 55 is the number of
corners of the 48 sectors of the seven regular polygons making up the inner form of the
Tree of Life.
4
elements needed to convert the Tree of Life with
48 elements into the 1-tree are their counterpart.
If we add together corners of sectors of polygons, there are only
two possible combinations of polygons with 21 corners of
their sectors:
4
+ 6 + 11 = 21, leaving 5 + 7 + 9
+ 13 = 34
and
5 + 7 + 9 = 21, leaving 4 + 6 + 11 + 13 = 34.
But neither case allows the Fibonacci number
21 to split into the Fibonacci numbers 8 and 13. Hence, combinations of corners of sectors do not
form Fibonacci numbers that are the sum of the two previous Fibonacci numbers. Either the centres of a
subset of the seven polygons are counted with the corners of other polygons (this case was analysed in
Article 503 or all seven centres are added to the corners of a subset of the seven polygons.
In view of the correspondences between the 55 corners of the sectors of these
polygons and the 55 geometrical elements of the 1-tree and between the seven
centres and the seven elements added to the Upper Face when the Tree of Life with 48
elements becomes the 1-tree, it follows that the seven centres should belong to the 34 corners of sectors, for this number is the number of elements in the Upper Face
containing the seven extra elements. The possible combinations are:
3 + 6 + 12 = 21 and (4 +
5 + 8 + 10) + 7 = 34,
4
+ 5 + 12 = 21 and
(3 + 6 + 8 + 10) + 7 = 34,
5 + 6 + 10 = 21 and
(3 + 4 + 8 + 12) + 7 = 34,
3 + 8 + 10 = 21 and (4 + 5 + 6 + 12) + 7 = 34,
and
3 + 4 + 6 + 8 = 21 and (5 + 10 + 12) + 7 = 34.
(’7’ denotes the seven centres). Only the last two combinations
shown above allow the split 21 = 8 + 13. This leaves the two possible compositions for the
remaining 34 corners of sectors:
(5 + 10 + 12) + 7 = 34,
and
(4 + 5 + 6 + 12) + 7 = 34.
Only the last one is consistent with the division 34 = 21 + 13
(13 = 7 + 6 and 21 = 4 +
5 + 12). Hence, this division is between the 21 corners of the triangle, octagon & decagon and the 34 corners of sectors that are either centres of the seven polygons or corners of the
square, pentagon, hexagon & dodecagon.
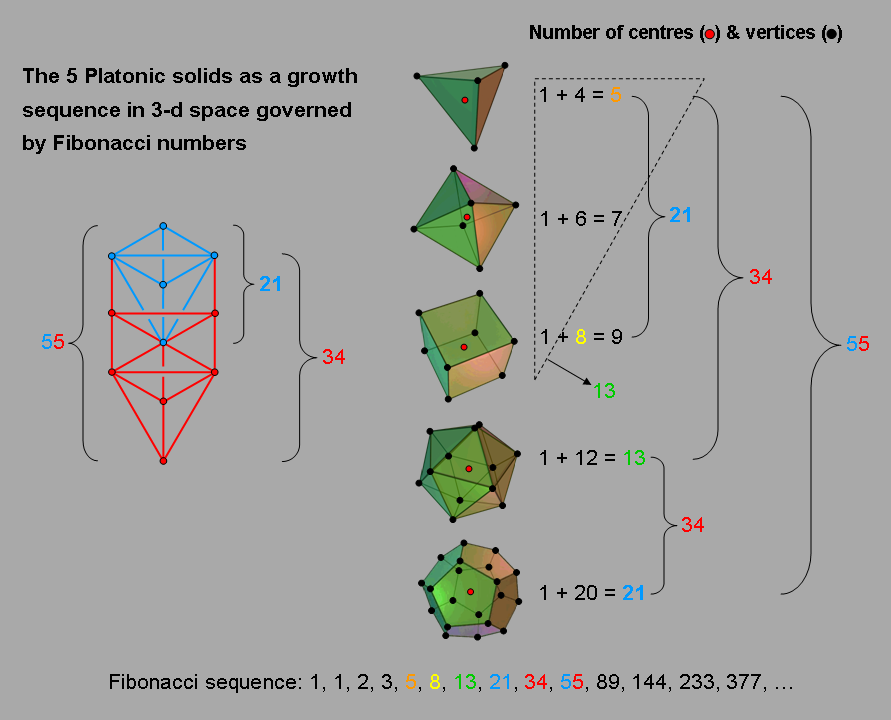
Figure 3. The corners and centres of the five Platonic solids form consecutive Fibonacci
numbers.
5
3. Fibonacci numbers in the Platonic
solids
As discussed in Article 50,4 the five Platonic solids have 55 vertices &
centres (Fig. 3). They comprise the 21 vertices &
centres of the tetrahedron, octahedron & cube and the 34 vertices &
centres of the icosahedron & dodecahedron. Notice that this 21:34 division splits the complete set of
5 regular polyhedra into two subsets: one of 2
solids and one of 3 solids, and that the numbers 2, 3 & 5 are consecutive
Fibonacci numbers. The 55 vertices & centres correspond to the
55 corners, edges & triangles making up the 1-tree. The
21 vertices & centres of the first 3 Platonic solids correspond to the traditional Upper Face of the Tree of Life rather
than to its Lower Face because, intuitively speaking, it is natural to associate the simplest solids with
the upper part of the Tree of Life, whose downward progression represents the development of more complex
forms from simpler ones. Indeed, its trunk (Fig. 4) consists of the sequence of the first four regular simplexes*: point→line
segment→triangle→tetrahedron. They are composed of 26 geometrical elements.5 YAHWEH (YHVH or יהוה)
prescribes the trunk, the value 10 of the first letter yod (Y or י) denoting the 10 vertices, the value 5 of the
first letter he (H or ה) denoting the
5 edges & triangles in the line segment and triangle, the value 6 of vav
(V or ו) denoting the 6 edges of the tetrahedron and the value 5 of the second he (H or ה) denoting the 5 triangles & tetrahedra
in the tetrahedron.
Figure 4. Geometrical composition of the trunk of the Tree of Life.
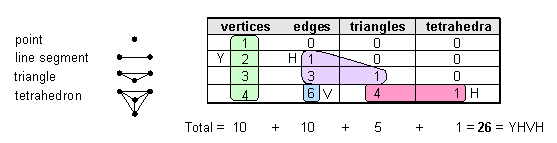
The 1-tree contains two tetrahedra (see Fig. 1) and
55 vertices, lines & triangles. These 57 geometrical elements correspond
to the 57 points that are either corners of sectors of the seven separate regular polygons of the inner
Tree of Life or the endpoints of the root edge that becomes their shared edge when they become enfolded
in one another. Their musical counterparts are the 57 notes in the first eight octaves. The 1-tree
consists of the 26 elements of its trunk prescribed by YAHWEH, the Godname of Chokmah,
and the 31 elements of its ‘branches’ prescribed by EL, which is the Godname of Chesed,
the Sephirah below Chokmah on the Pillar of Mercy of the Tree of Life. One of these elements is the
eleventh vertex located at Daath and another is the tetrahedron in the Upper Face. The two elements
correspond to the tonic and to the eighth octave — the 57th note. This leaves 29 geometrical elements
(15 edges, 14 triangles) in its branches that correspond to the 29 partials in the first
55 notes of the Pythagorean scale above the tonic. The 26
elements in the trunk correspond to the 26 notes that are overtones. This means that the
55 vertices, lines & triangles making up the 1-tree do not correspond to
these 55 notes, for they do not include the tetrahedron that corresponds to
one of the 26 overtones. The two endpoints of the root edge correspond to the vertex
located at Daath and to the tetrahedron in the Upper Face. The 55 corners of
sectors correspond to the remaining 55 vertices, lines, triangles &
tetrahedra in the 1-tree. The 48 corners of sectors correspond to the
48 vertices, edges & triangles of the Tree of Life, whilst the seven centres
correspond to the 3 edges, 3 triangles &
one tetrahedron added when the Tree of Life becomes the 1-tree.
Figure 3 indicates that the numbers of points, lines & triangles in
the sets of 21 and 34
are:
21 = 5t +
16b,
and
34 = 20t + 14b,
where the suffixes ‘t’ and ‘b’ refer to the trunk and to the branches of
the 1-tree. The tetrahedron has 5 vertices & centres and the octahedron
& cube has 16 vertices & centres. The icosahedron has 13 vertices &
centres and the dodecahedron has 21 vertices & centres.
Hence, the regular polyhedral counterparts of the 5 triangles and 20 vertices
& edges of the trunk of the Tree of Life is the 5 vertices & centre of
the tetrahedron and the 20 vertices of the dodecahedron. Their musical counterparts are the 25 overtones
above the first octave in the first 55 notes. The polyhedral counterparts of
the branches of the 1-tree composed of 16 vertices & edges and 14 triangles are the 16 points that are
either vertices of the icosahedron or centres of the octahedron, cube, icosahedron & dodecahedron and
the 14 vertices of the octahedron and cube.
* A regular n-simplex is the n-dimensional analogue of an
equilateral triangle. The 0-simplex is the point, the 1-simplex is the line segment (or straight line),
the 2-simplex is the triangle and the 3-simplex is the tetrahedron.
6
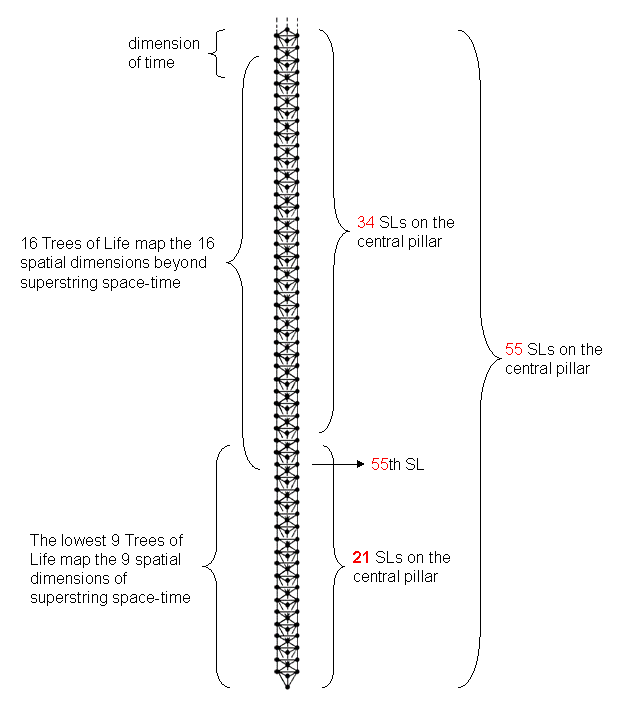
Figure 5. The lowest 26
Trees of Life map 26-dimensional space-time.
21 SLs lie on the central pillar of the
lowest 9 Trees mapping the 9 spatial dimensions of
superstrings. 34 SLs lie on the central pillar
of the next higher 16 Trees mapping the 16 higher spatial dimensions. The
26th Tree maps the dimension of time.
4. YAHWEH prescribes the seven musical scales
It is not by accident
that the first 55 notes above the tonic of the Pythagorean scale should include
26 overtones. We have seen in previous articles6,7 that YAHWEH prescribes the seven types of musical scales because they constitute
another holistic system. Table 3 lists the tone ratios of their notes:
7
Table 3. The tone ratios of the notes in the seven musical
scales.
(White cells denote Pythagorean notes between the tonic and octave in grey cells).
| Musical scale |
Tone ratio
|
| B scale |
1 |
256/243 |
32/27 |
4/3 |
1024/729 |
128/81 |
16/9 |
2 |
| A scale |
1 |
9/8 |
32/27 |
4/3 |
3/2 |
128/81 |
16/9 |
2 |
| G scale |
1 |
9/8 |
81/64 |
4/3 |
3/2 |
27/16 |
16/9 |
2 |
| F scale |
1 |
9/8 |
81/64 |
729/512 |
3/2 |
27/16 |
243/128 |
2 |
| E scale |
1 |
256/243 |
32/27 |
4/3 |
3/2 |
128/81 |
16/9 |
2 |
| D scale |
1 |
9/8 |
32/27 |
4/3 |
3/2 |
27/16 |
16/9 |
2 |
| C scale |
1 |
9/8 |
81/64 |
4/3 |
3/2 |
27/18 |
243/128 |
2 |
There are 26 Pythagorean notes between the tonic
and octave:
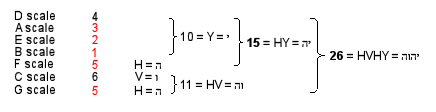
YAHWEH (YHVH) prescribes the seven scales, its four letter values
being the numbers of Pythagorean notes in four sets of scales. Alternatively, the letter values are the
numbers of four sets of notes:
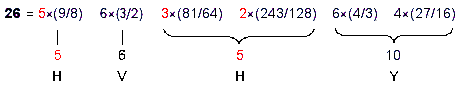
This property of a single octave of the Pythagorean scale is the
counterpart of the 26 overtones in the first 55 notes after
the tonic of eight octaves of this scale — another holistic set.
As they are both parameters of a holistic system, the numbers
26 and 55 are always found associated with each other in
sacred geometrical representations of such systems. This, too, is the case, arithmetically speaking, because
the sum of the first ten integers arranged in a tetractys is 55, whilst
26 is the number of the combinations of the integers in each row:
Number of combinations
1
1
2 3
3
55 =
4 5
6
7
7 8 9 10
15
Total = 26
Another example of this association is the fact that there are 55 SLs on the central Pillar of Equilibrium of the lowest 26 Trees of Life
in CTOL (Fig. 5). The Malkuths of these Trees of Life can be regarded as corresponding to the
26 overtones and the remaining 29 SLs on this pillar can be thought of as corresponding to
the 29 partials. The correspondence demonstrates that the notes of the Pythagorean scale conform to an
underlying Tree of Life pattern. 21 SLs span the central
pillar of the lowest nine Trees of Life. As a map of the 26-dimensional space-time
predicted by quantum mechanics for spinless strings, each Tree of Life in this context denotes a dimension.
The 9-tree represents the nine spatial dimensions predicted by superstring theory. Hence, the
21:34 division of 55 found earlier for the first 3 of the 8 octaves spanned by 55 notes has its counterpart in string
theory as the distinction between the nine superstring and 16 bosonic dimensions of space. Fibonacci numbers
define the demarcation between the two types of dimensions! The Fibonacci number 5 determines the 1-tree with 5 SLs on its central pillar and
the number 13 determines the 5-tree with
13 SLs on its central pillar. The counterpart of the 21:34 division of SLs on the central pillar of the
26-tree is the transition from the Upper Face of the 1-tree with 34 geometrical elements to its Lower Face with 21 elements. Its counterpart in the 5 Platonic solids
is the transition from the first four solids with 34 vertices & centres to
the final solid — the dodecahedron — with 21 vertices &
centre (see Fig. 3). In Article 50 (Part 1), it was pointed out that the faces of the five
8
Platonic solids have 550 (=55×10) corners,
edges and sectors. The faces of the first four Platonic solids have 210 (=21×10) polyhedral corners, edges & sectors, leaving 340(=34×10) corners, edges & sectors.8 Once again, the 21:34 division differentiates the dodecahedron from the first four regular polyhedra. The
ancient Greeks believed that the latter were the shapes of the particles of the Elements of Earth, Water,
Air and Fire making up the physical universe. Through the shared Fibonacci number 21, they are associated with superstring space-time with nine spatial dimensions,
whilst the fifth Platonic solid representing the fifth Element Aether is associated through the Fibonacci
number 34 with the purely bosonic string dimensions of space-time.
The tenth Fibonacci number 55 determines the
nine superstring dimensions in another way. The 55th SL from the bottom of CTOL is
Chesed of the ninth Tree of Life mapping the ninth of the spatial dimensions of superstrings. This SL is the
496th SL from its top. The tetractys representation of the 550 SLs of CTOL:
55
55 55
550
= 55 55 55
55 55 55 55
implies that the central number 55, which
occupies the position of the point symbolizing Malkuth in the tetractys counterpart of the Tree of Life,
characterizes the physical universe in a fundamental way. Remarkably, the gematria number value of Malkuth
is 496 (see Table 1). Even more remarkably, this is the number of spin-1 gauge bosons that
mediate the unified interactions between superstrings with nine spatial dimensions mapped by the nine lowest
Trees in CTOL. We saw earlier that the 21:34 division of SLs on the central pillar of CTOL demarcates the nine superstring dimensions
from the 16 bosonic string dimensions. The 21:34 division of all SLs up to the first Sephirah of Construction of the ninth Tree of Life
distinguishes the 3 large-scale dimensions of space from the 6 compactified
dimensions of superstrings because, counting from the bottom of CTOL, there are 21 SLs up to Binah of the third Tree of Life mapping the third spatial dimension
and 34 SLs in the next 6 Trees of Life above it up to Chesed of the ninth Tree
of Life. Below are listed analogous examples of the fundamental bifurcation of holistic systems created by
these Fibonacci numbers:
21
34
1st 3
octaves 1st
5 octaves
last
15
overtones 1st
11 overtones
Lower
Face of
1-tree 1-tree
outside its Lower Face
1st 3 Platonic solids or
dodecahedron icosahedron
& dodecahedron or 1st four Platonic solids
9 superstring
dimensions 16
bosonic string dimensions
3
large-scale
dimensions 6
compactified dimensions
A musical chord is a set of 3 or more notes that sound
simultaneously. There are some combinations of 3 notes that, when played
together, produce a sensation of harmony, rest and stability. They are the so-called ‘consonant chords’ and
there are only two types of them: major and minor chords. The rest of the chords are dissonant. An example
of a consonant chord well-known to musicians is the C major chord composed of the notes C, E & G. They
are the first, third & fifth notes of the eight-note Pythagorean scale. The numbers 1, 3, 5 & 8 are all Fibonacci numbers. The following consideration indicates that this is not
coincidence but indicative of how the human ear is tuned to a harmony determined by the Fibonacci numbers,
just as the connection of the latter to the Golden Ratio has been recognised by artists and architects as
creating forms with proportions that please the eye: the first 21 notes after the tonic span 3 octaves, the next
34 notes span 5 octaves and 55 notes are between the tonic and 8th octave. The same
Fibonacci numbers re-appear! Just as the octave is a musical whole of 8 notes,
so these 55 notes solely belonging to 8 octaves
constitute another analogous whole in which each note is replaced by an octave. Just as there are 27
intervals less than an octave between the 8 notes of a musical scale, so
there are 27 harmonics (notes with integer tone ratios) below the 8th octave.
The 21:34 division separates the
first 3 octaves from the last 5. Its counterpart
in the single octave is E, the major second, and its

Figure 6. The Sri Yantra.
inversion (the interval between it and the first octave). The
34:21 division separates the
first 5 octaves from the last 3 octaves. Its
counterpart is G, the perfect fifth. In terms of the letter values of YHVH, the division is set by that
between VH and YH. The perfect fifth represents the fundamental division of the octave interval. It is
set by this ancient division of Tetragrammaton, the sacred Name of God, because YAH (Hebrew: YH) was the
form used particularly by the prophet Jacob and his people.9
5. The 21:34 division in the
2-dimensional Sri Yantra
Revered by Hindus as the most powerful and sacred of the Yantras,
or meditative images, the Sri Yantra (Fig. 6) consists of nine interlocking triangles. Five triangles point downwards and four
triangles point upwards. This generates 42 triangles arranged in four sets of 8, 10, 10 & 14. They
surround a downward-
8
pointing triangle at the centre of which is a point, or bindu. Article 3510 analysed the 2-dimensional Sri Yantra, showing its equivalence to the Tree of
Life because the former consists of 70 points and the 43 triangles of the latter comprise 70 points when its
16 triangles are tetractyses (Fig. 7).
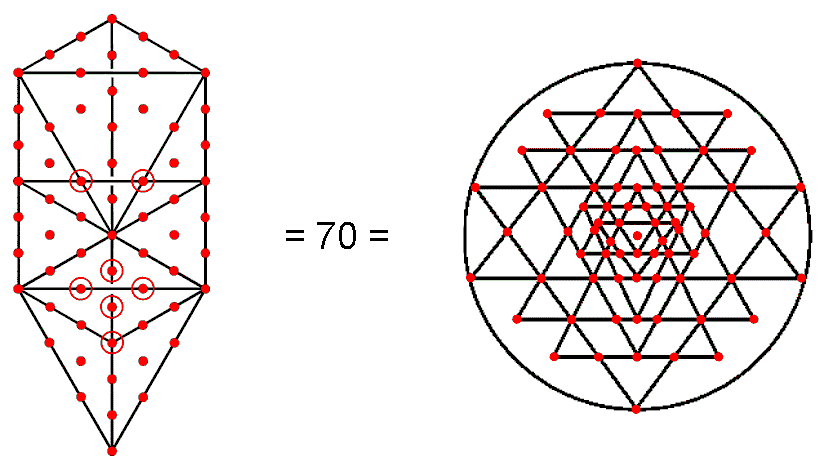
Figure 7. The equivalence of the Tree of Life and the Sri Yantra.
Two of them — the central point called the “bindu”
and the lowest corner of the central, downward-pointing triangle — are unshared with the 42 surrounding
triangles.
Hence, 68 corners of the latter surround the central triangle,
34 corners per set of 21 triangles in each half of the Sri Yantra. There are (34+21=55) corners
& centres of these 21 triangles (Fig. 8).
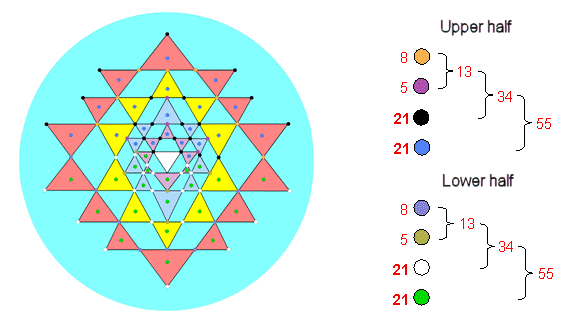
Figure 8. The Fibonacci number pattern in each half of the 2-dimensional
Sri Yantra.
The primary 21:34 division found in other sacred geometries
differentiates between the corners and centres of the triangles in each half of this ancient symbol of
divine creation. It also differentiates between the fourth set of 14 triangles, which have
21 corners & centres, and the first three sets of 28
triangles, which have 34 corners & centres. Below are listed the
Fibonacci numbers in the 21 triangles in each half of the
Sri Yantra:

10
The 34 corners & centres of the first
three sets comprise 13 corners & centres of the second set and
(11+10=21) corners & centres of the first and third sets.
The 13 corners & centres of the second set comprise 5 centres and (3+5=8) corners, 3 of which touch
sides of triangles. The 21 corners & centres of the first and third sets comprise groups of
8 ((1+2)+5 =3+5) and 13 (5+4+4=5+8). Of the 34 corners,
13 corners either touch sides of triangles (1+2+3) or are the seven outer
corners of the fourth set of triangles, leaving 21 other
corners (7+5+5+4).
Comparing the 55 corners & centres
of each half of the Sri Yantra with the 55
corners, edges & triangles of the 1-tree, the 21 centres
of triangles in each half correspond to the 21 geometrical
elements in the Lower Face and the 34 other corners & centres in each half
correspond to 34 geometrical elements in the
remainder of the 1-tree.


Figure 9. This sunflower has 55 spirals
of florets arranged in 34 clockwise spirals and 21 anticlockwise spirals.
Finally, an example of how the 21:34 division manifests in flowers is the
21 anticlockwise spirals and 34
clockwise spirals of florets in some sunflowers (Fig. 9), although they manifest other pairs of successive Fibonacci numbers as well. Such
numbers optimise the packing of florets so that they occupy equal space, maximising the amount of sunlight
to which they can be exposed. On many plants, the number of petals is a Fibonacci number. The aster,
black-eyed susan and chicory have 21 petals; plantain and
pyrethrum both have 34 petals.11 The Lucas numbers, which are related to Fibonacci numbers,12 also appear sometimes in flowers. We now see
that the distinction between 21 and 34 is one that manifests not only in the world of plants but also in the notes of the
Pythagorean musical scale and in the dimensions of the space-time of the infinitesimally small superstrings,
demarcating the Lower Face of the Tree of Life blueprint from its Upper Face, i.e., the personal and
transpersonal levels of consciousness, as well as the centres of the triangles in each half of the Sri
Yantra and their corners. Such universality is aptly embodied in the hermetic principle “As above, so
below.”
References
1An excellent discussion of
Fibonacci numbers and the Golden Section is “The Golden Section,” by Scott Olsen, Wooden Books Ltd, 2006.
2 Phillips, Stephen M. Article 50 (Part 1): “The Golden Ratio, Fibonacci and Lucas numbers
in sacred geometries,” (WEB, PDF), pp. 7, 8.
3 Ibid, pp. 17, 18.
4 Ibid, pp. 31, 32.
5 Phillips, Stephen M. Article 33: “The human axial skeleton is the trunk of the Tree of
Life,” (WEB, PDF), p. 8.
6 Phillips, Stephen M. Article 14: “Why the ancient Greek musical modes are sacred,”
(WEB, PDF), p. 9.
7 Phillips, Stephen M. Article 31: “The musical nature of the polyhedral Tree of Life,”
(WEB, PDF), pp. 6, 7.
8 Ref. 2, pp. 33, 34.
9 Schaya, Leo: “The Universal Meaning of the Kabbalah,” Unwin Paperbacks, 1989, p.
153.
10 Phillips, Stephen M. Article 35: “The Tree of Life Nature of the Sri Yantra and some of
its scientific meanings,” (WEB, PDF).
11 http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html#petals.
12 Ref. 1, p. 16 and ref. 2, p. 9.
Home