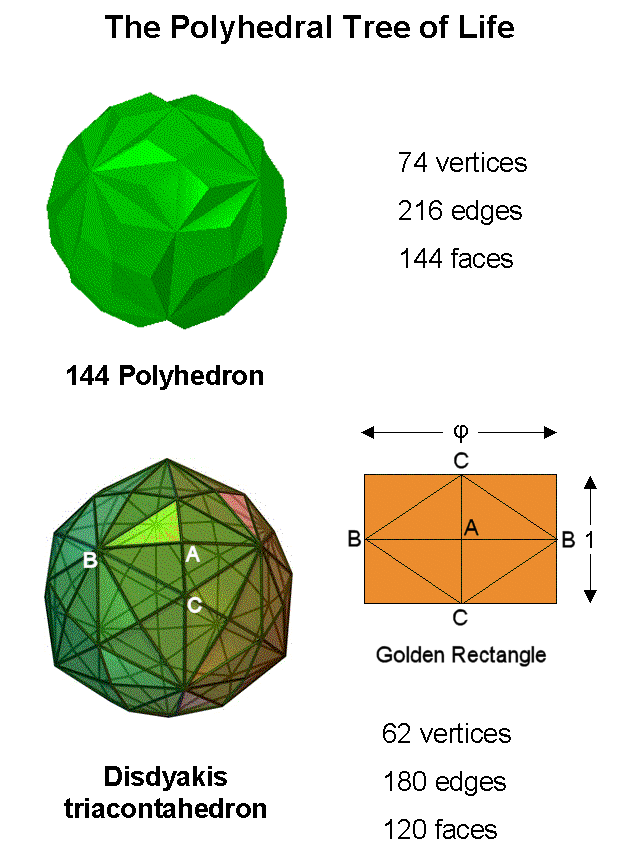
The two polyhedra of the Polyhedral Tree of Life.
| << Previous 1... 5 6 [7] 8 9 Next >> |
#6 The Polyhedral Tree of Life
|
|
|
|
The two polyhedra of the Polyhedral Tree of Life. |
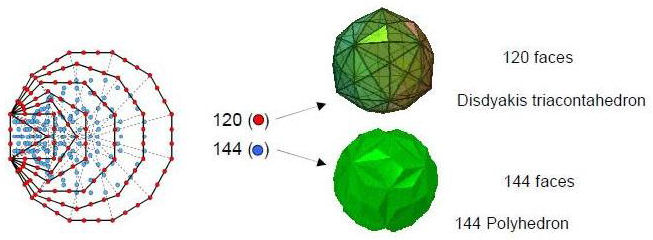
The 120 yods on the sides of the 7 enfolded polygons of the inner Tree of Life symbolise the 120 faces of the disdyakis triacontahedron and the 144 yods inside these polygons symbolise the 144 faces of a polyhedron with 74 vertices ("144 Polyhedron"). |
The boundary of the seven enfolded polygons is the shape, or outer form, of the inner Tree of Life. It is measured by the 120 yods (36 corners, 84 hexagonal yods) that line their sides. Inside the boundary of the seven envolded polygons are 144 yods, creating a total of 264 yods. 120 is the sum of the ten odd integers after 1:
120 = 3 + 5 + 7 +9 + 11 + 13 + 15 + 17 + 19 + 21,
and 144 is 122, where 12 is the number of corners of the dodecagon, the tenth regular polygon. As 264 = 66×4, where 66 is the sum of the first 11 integers, 264 is the sum of the 11 even integers that start with 4 and are four units apart:
264 = (4+8+12+16+20+24+28+32) + (36+40+44) = 144 + (36+84) = 144 + 120.
This is the arithmetic counterpart of the 144 interior yods, the 36 corners and the 84 hexagonal yods on sides of the seven enfolded polygons making up the inner Tree of Life.
Is this exterior/interior distinction that is displayed in the polygonal, inner form of the Tree of Life realized in a polyhedral counterpart of the 120:144 division? If so, how? These questions were answered here. Whilst there is a Catalan solid with 120 faces (the maximum shown in a Catalan solid), there is not an Archimedean solid with 144 faces. However, the Catalan solid called the "disdyakis dodecahedron" has 48 triangular faces. Sticking tetrahedra on its faces creates a required polyhedron with 144 faces. Adding square pyramids with four faces to an Archimedean or a Catalan solid cannot create such a polyhedron because there is none that has 36 faces. Only one member of the 26 Archimedean & Catalan solids can therefore generate a polyhedron with 144 faces. The disdyakis dodecahedron has 26 vertices, 72 edges & 48 faces. Adding tetrahedra to the latter creates a polyhedron with (26+48=74) vertices, (72 + 3×48 = 216) edges and (48×3=144) triangular faces. This will be called the "144 Polyhedron." The 120:144 division therefore manifests in the pair of polyehdra consisting of the disdyakis triacontahedron with 62 vertices, 180 edges and 120 triangular faces and the 144 Polyhedron with 144 triangular faces. The former is created by sticking rhombic-based pyramids onto the 30 faces of another Catalan solid called the "rhombic triacontahedron." The faces of the latter are Golden Rhombi, that is, rhombi that can be enclosed by Golden Rectangles, whose adjacent sides have lengths in the proportion of the Golden Ratio Φ = (1+√5)/2 = 1.618.... The peaks of the rhombic pyramids will be called "A vertices." The vertices at the ends of the longer diagonal of the Golden Rectangle will be called "B vertices" and the ends of the shorter diagonals will be called "C vertices." The 62 vertices of the disdyakis triacontahedron comprise 30 A vertices, 12 B vertices & 20 C vertices. The B vertices are the vertices of an icosahedron and the C vertices are those of a dodecahedron. The rhombic triacontahedron is their compound,
Consider the 144 Polyhedron to be inside the disdyakis triacontahedron, their centres coinciding.* Suppose that their (74+62=136) vertices are joined by straight lines to this common point, creating (144+120+180+216=660) triangles with 137 corners. We see that the Polyhedral Tree of Tree (the polyhedral version of its inner form) embodies the number 137 associated with the fine-structure constant as the least number of points in space needed to shape all the triangles that compose the exterior and interior of its two polyhedra. It is the sum of 1 (the centre shared by the two polyhedra) and 136, which is the 16th triangular number:
| 1 | 2 | 3 | 4 | |
| 136 = | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | |
| 13 | 14 | 15 | 16 |
When separate, the two polyhedra are made up of 660 triangles with 138 corners, where
138 = 2 + 62 + 74 = 64 + 74.
The counterpart of this in the Tetrahedral Lambda discussed in #4 is the sum of the 10 numbers that are arranged along the three raised edges of the tetrahedron:
138 = (1+2+4+8+3+9+27+4+16) + 64 = 74 + 64.
The 74 vertices of the 144 Polyhedron correspond to the sum of the nine integers below the largest one (64), which is the sum of the number of vertices of the disdyakis triacontahedron and the two separate centres.
Half of the 144 Polyhedron has 37 vertices and half of the disdyakis triacontahedron has 31 vertices, a total of 68 vertices in each half of the pair of polyhedra. Hence, 138 = 1 + 68 + 1 + 68 = 2 + 2×68. This pattern manifests in the last of the seven regular polygons making up the inner Tree of Life, namely, the dodecagon, which is the polygonal form of the outer Tree of Life:
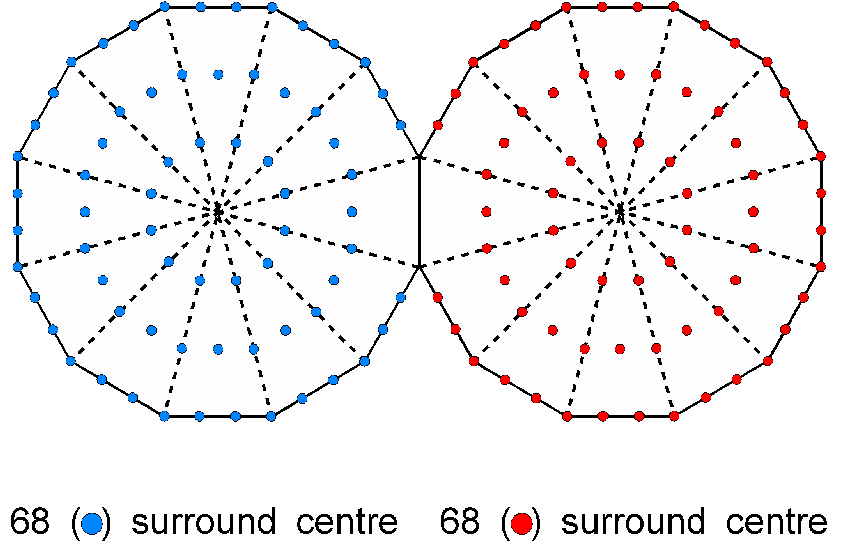
Outside the root edge, there are 68 yods in each dodecagon that surround its centre. The two dodecagons represent the two halves of the pair of polyhedra, their two centres corresponding to the centres of the latter.
* The next page will reveal why the Polyhedral Tree of Life must have the disdyakis triacontahedron enclosing the 144 Polyhedron.