The 50 regular polygonal faces of the five Platonic solids have 180 sectors.
| << Previous 1... 4 5 [6] 7 8 ...9 Next >> |
#5 The five (and the first four) Platonic solids embody the number 137

The 50 regular polygonal faces of the five Platonic
solids have 180 sectors.
The five Platonic solids are the only regular polyhedra that can exist. They are an example of "sacred geometry" not because the ancient Greeks believed that particles of the five Elements Earth, Water, Air, Fire & Aether have their shapes (they were half-right — many chemical molecules, not atoms, have their forms) but because their shapes — individually and collectively — embody the universal pattern found in other holistic systems (see The holistic pattern). Because of their archetypal status, their properties are quantified by the same numbers that are shown in many sections of this website to parameterise other sacred geometries or holistic systems embodying this pattern. Among these are the number 137 and the number 1370, as we shall now show by constructing the faces and interiors of each Platonic solid from triangles, which we then turn into tetractyses.
First consider the centroids of the 50 triangular, square and pentagonal faces of the Platonic solids, which have 90 edges. Joining them to the vertices shaping each face creates 180 sectors. Then consider the centre of mass of each solid (its geometric centre) and join it to all its vertices. This creates 50 sides of 90 internal triangles. Because regular polygonal faces have divided into their sectors, we must divide internal triangles into their three sectors in order to be consistent with the procedural rules for building the Platonic solids out of simple triangles that we then turn into tetractyses. The total number of corners surrounding the centres of the Platonic solids = 50 + 50 + 90 = 190. The total number of sides = 90 + 180 + 50 + 90×3 = 590. The total number of triangles = 180 + 90×3 = 450. The total number of geometrical elements surrounding the centres = 1230. Therefore, on average, a Platonic solid has (1230/5 = 246) geometrical elements surrounding its centre, each half having 123 geometrical elements surrounding its centre (19 points, 59 lines & 45 triangles). The number 246 is the number value of Gabriel, the Archangel of Yesod.
Now let us turn each simple triangle into a tetractys. The table below lists the yod population of each solid:
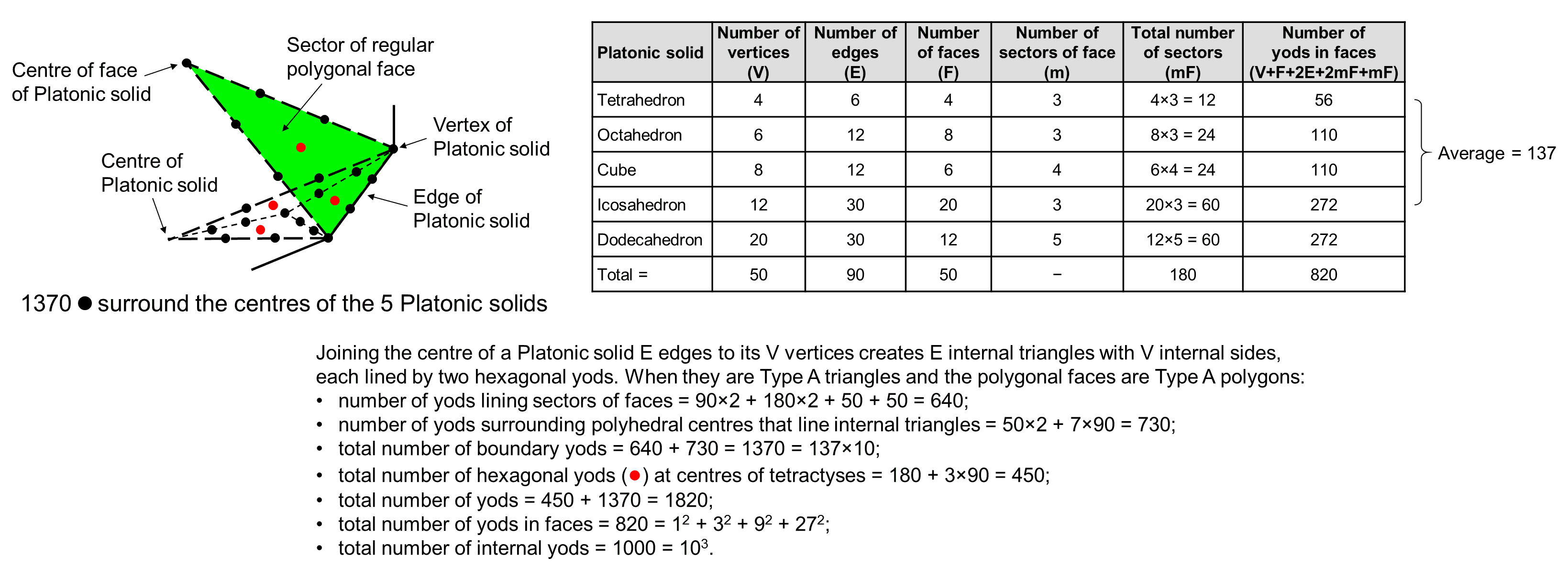
The average number of yods in the faces of the first four Platonic solids is 137. This shows how Feynman's "magic number" 137 shapes the Platonic solids that the ancient Greeks thought were the shapes of the four physical Elements Earth, Water, Air & Fire. The average number of vertices per Platonic solid is 10, so that the average of yods needed to construct the faces of a Platonic solid from tetractyses is 127. This is the 31st prime number, where 31 is the number value of EL (אל), the Godname assigned to Chesed. The total number of yods in the 50 faces of the Platonic solids is 820, where
820 = 12 + 32 + 92 + 272 = 30 + 32 + 34 + 36 = 90 + 91 + 92 + 93,
i.e., it is the sum of the squares of the four integers 1, 3, 9 & 27 on one side of Plato's Lambda (see #4).
The sum (90) of the ten integers in the Lambda Tetractys correspond to the 90 edges of the five Platonic solids. The tetrahedron and the dodecahedron (or icosahedron) have 36 edges and the octahedron, cube & icosahedron (or dodecahedron) have 54 edges. This is the regular polyhedral manifestation of the fundamental 36:54 division of holistic systems (see here), as expressed in the first face of the Tetrahedral Lambda. The sum of the three interpolated integers 6, 12 & 18 is 36 and the sum of the seven integers forming the Lambda is 54. The central integer 6 denotes the six edges of the tetrahedron and the sum (30) of the two other interpolated integers is the number of edges in the icosahedron (or dodecahedron). The number 90 with the 36:54 division is a parameter of holistic systems.
1820 yods surround the centres of the five Platonic solids. Of these, 450 yods are hexagonal yods at centres of tetractyses. Therefore, (1820−450=1370) yods surround the centres of the five Platonic solids and line all the sides of their 450 tetractyses. The number that shapes the five Platonic solids is identical to the yod population of the inner Tree of Life composed of Type B polygons (see #2). This is no coincidence, for both this mathematically complete set of regular polyhedra and the inner Tree of Life are archetypal in nature, being parameterised by certain powerful numbers such as 137, which only seems "magical" because physicists cannot as yet explain its magnitude. On average, 137 yods in each half of a Platonic solid line its tetractyses. They comprise 64 yods in its faces and 73 inside it, where 64 is the number value of Nogah, the Mundane Chakra of Netzach, and 73 is the number value of Chokmah. Including the centre to either half of a Platonic solid, the number 138 appears as the sum of 137 and 1, which is the starting point for the construction of the Platonic solids, including the imaginary one possessing their average properties. This is analogous to the sum (138) of the 10 integers on the three raised edges of the Lambda Tetrahedron, being the sum of the integer 1 at its apex and the sum (137) of the nine powers of 2, 3 & 4 arranged along these edges (see #4).