| << Previous 1... 5 6 7 8 [9] Next >> |
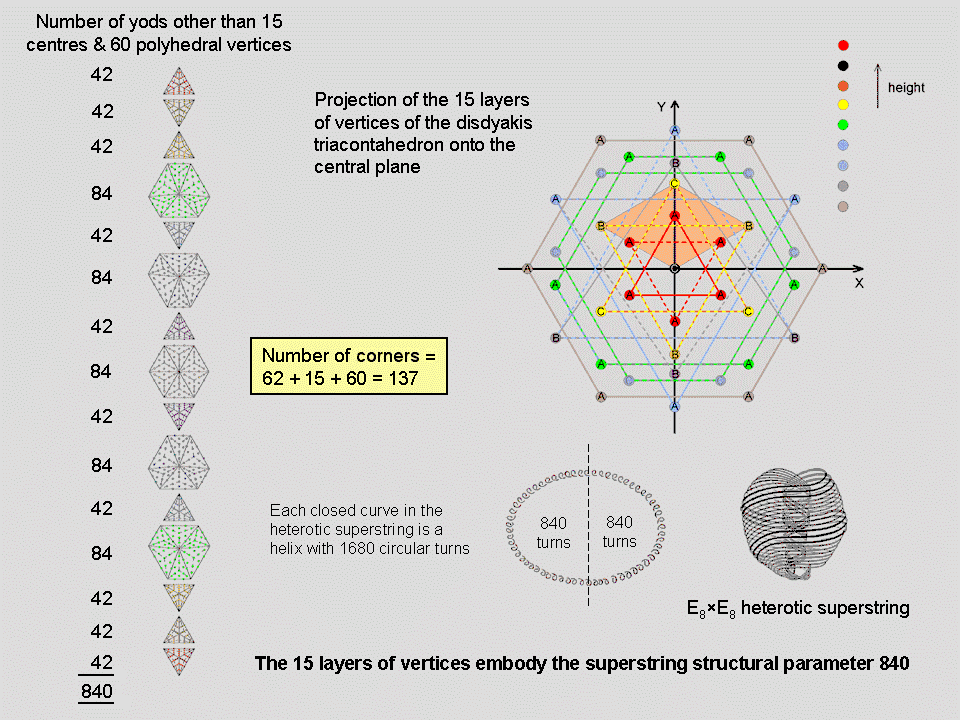
#8 The disdyakis triacontahedron embodies the number 137 and the superstring structural parameters 840 & 1680

The number of yods in an n-gon with each of its n sectors a Type A triangle is 15n + 1, where "1" denotes its centre. 14 n yods other than its corners surround the centre of an n-gon. When the axis of the disdyakis triacontahedron passes through two diametrically opposite C vertices (it has 20 C vertices forming a dodecahedron), the 60 vertices that surround this axis form the corners of 15 polygons, seven on either side of a central hexagon. The graph displays their vertices projected onto the central XY plane. If one imagines their 60 sectors turned into Type A triangles, the number of yods other than polyhedral vertices that surround their 15 centres = ∑14n = 14∑n = 14×60 = 840. This is the number of turns in the outer or inner half of each helical whorl of the UPA, which is the subquark state of the E8×E8 heterotic superstring. As well as embodying the superstring structural parameter 840 as the number of points, lines & triangles that make up each half of this polyhedron, the disdyakis triacontahedron embodies the same number as the 840 new yods that are needed to construct the sectors of its 15 polygons from Type A triangles. It demonstrates the truly remarkable properties of this Catalan solid, as well as confirming its status as the polyhedral form of the universal blueprint for both the structure and group dynamics of the E8×E8 heterotic superstring.
Embodiment of the number 137 determining the
fine-structure constant
Between the two opposite C vertices of the disdyakis
triacontahedron are 15 polygons with 60 corners. When their sectors are
Type A triangles, their (60×3=180) triangles have (60+15+60=135) corners.
Therefore, there are (2+135=137) points that are corners of triangles making up either polygons,
faces or both. The number 137 is the 33rd prime number, where 33 = 1! + 2! + 3! +4!, showing how
the integers 1, 2, 3 & 4 symbolised by the four rows of the tetractys express this number.
It is at the heart of quantum electrodynamics because it determines the fine-structure constant α = 1/137.03599911… measuring the strength of
the coupling of an electron to the electromagnetic field. The 137 points comprise the 17 points
on the axis passing through the two C vertices (15 centres of polygons
& two C vertices) and the 120 (= 22 + 42 +
62 + 82) points that are either polyhedral vertices or corners shared
by the triangles making up each sector. The same 17:120 division of the holistic parameter 137
appears in the first four Platonic solids as, on average, the 17 corners of triangles and the
120 hexagonal yods that make up their faces (see here).
This is a remarkable example of the correspondence between sacred geometries. In more detail,
the correspondences are:
|
First four Platonic solids (average) |
Disdyakis triacontahedron |
| 17 corners of triangular sectors in faces; | 17 points on C-C axis; |
| 30 hexagonal yods at centres of tetractyses or on edges in each half; | 30 vertices in each half; |
| 30 hexagonal yods on internal sides of tetractyses in each half; | 30 corners of triangles in polygons in each half. |
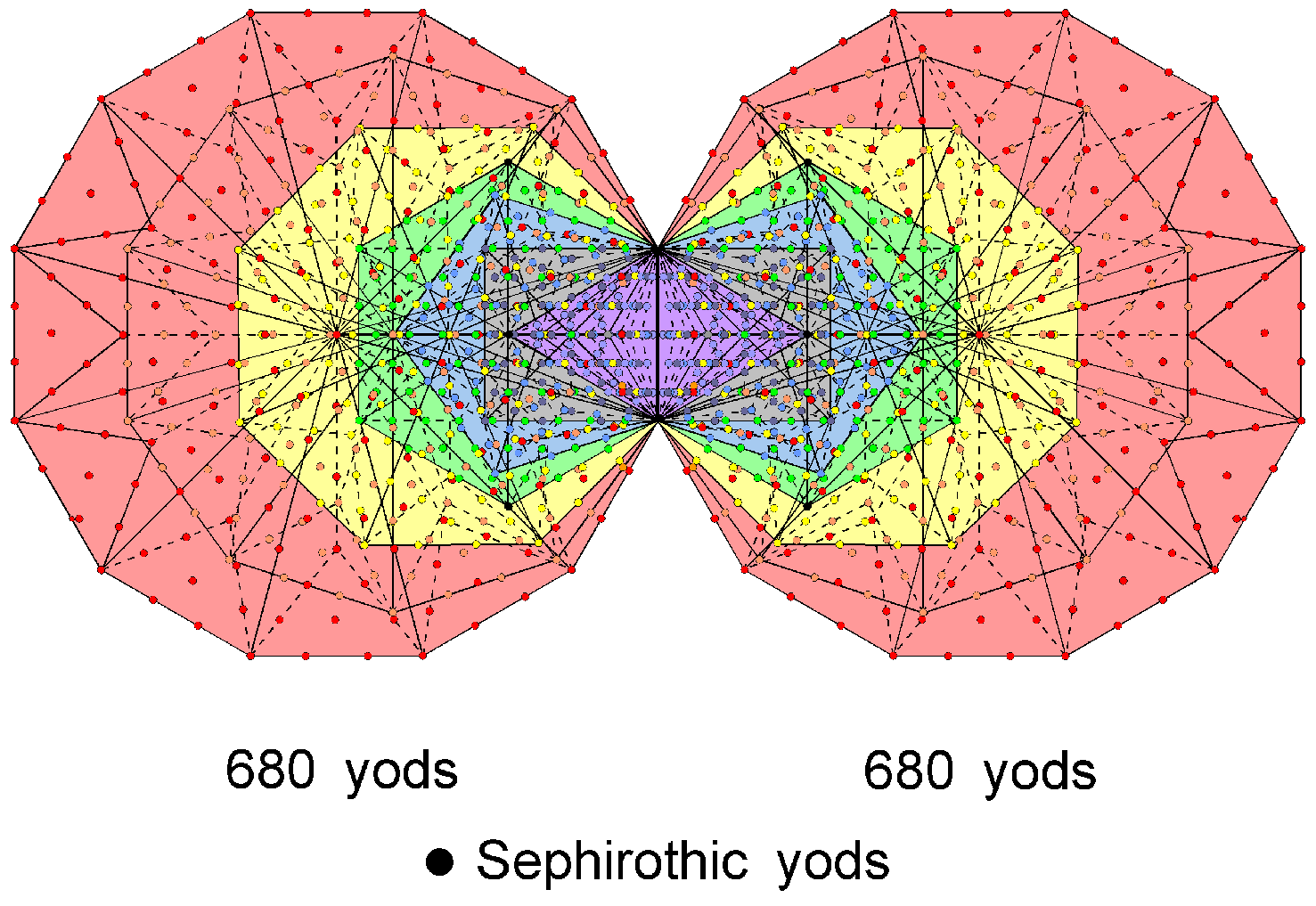
There are 68 corners or vertices in each half of the disdyakis triacontahedron that surround its centre. The counterpart of this in the inner Tree of Life are the 680 (=68×10) yods outside the root edge in each set of seven enfolded Type B polygons that do not coincide with the Sephirothic points (shown below as black yods) on each side pillar of the outer Tree of Life:
It also manifests in the pair of joined Type A dodecagons as the 68 yods in each polygon outside their shared edge that surround their centres:
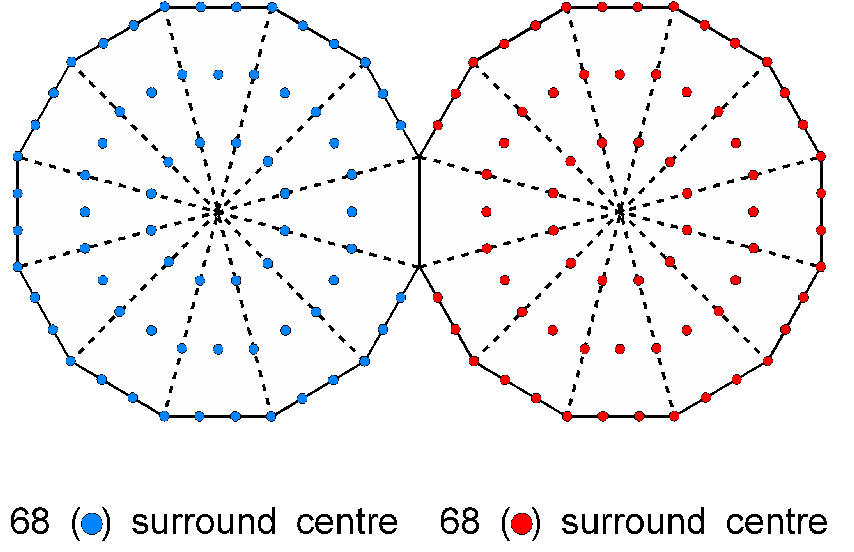
This demonstrates how the Decad determines through the tenth regular polygon properties of sacred geometries that are analogous to its own properties.
| << Previous 1... 5 6 7 8 [9] Next >> |