#17 Correspondence between the polygons in the disdyakis triacontahedron and other sacred geometries

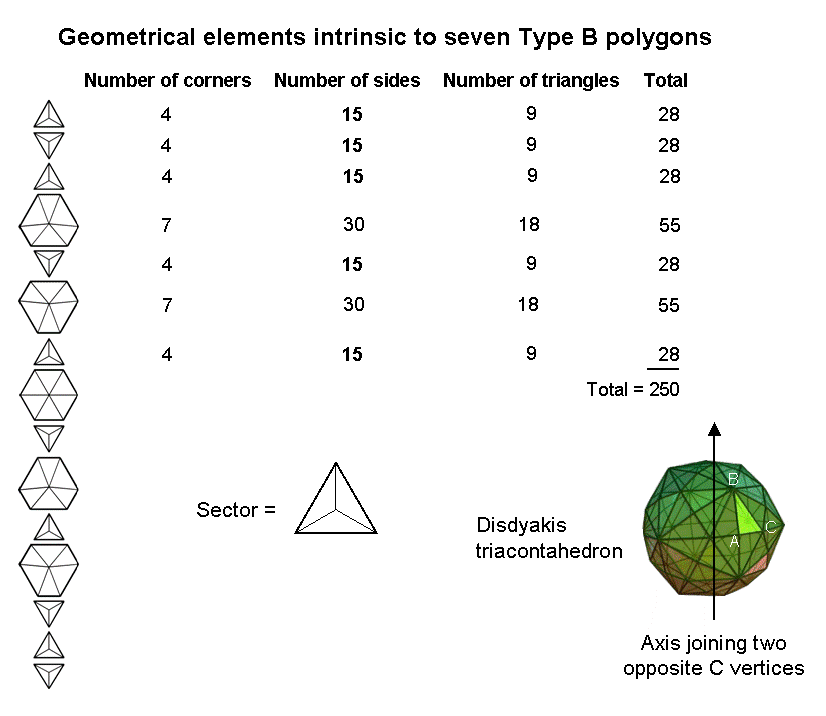
The disdyakis triacontahedron is the polyhedral version of the inner form of the Tree of Life. It has 120 triangular faces with vertices labelled A, B & C. Its 20 C vertices are the vertices of a dodecahedron. Consider an axis that passes through two diametrically opposite C vertices. As pointed out in Article 36, the 60 vertices that surround this axis are the corners of 15 polygons stacked one above another in parallel planes. The polygon in the middle is a hexagon with six A vertices. Above and below it is a set of seven polygons, one set being the inversion of the other. As all the vertices in a given polygon are of the same type (either A, B or C. See Table 1 on p. 3 of Article 36), the sides of the polygons are not edges of the polyhedron. Let us regard each polygon as a Type B polygon, that is, its triangular sectors are divided into three new sectors. This creates a new corner, three new sides and three new triangles. The table displays the corners, sides & triangles in a set of seven Type B polygons that are intrinsic to them in the sense that none of them is part of the disdyakis triacontahedron. We see that they contain 250 geometrical elements. As discussed in #16, this is:

• the sum of the 16 integers in the Tetrahedral Lambda other than those at its vertices;
• the number of corners of the first six types of polygons enfolded in 10 Trees of Life that are intrinsic to them;
• the number of yods intrinsic to the 1-tree when its triangles are Type A triangles;
• the number of yods in a pair of joined Type C triangles.

Moreover, the two 6-sided polygons have 50 corners & triangles, leaving 200 geometrical elements (the table indicates that this is the only combination of 50 elements). This 50:200 division corresponds to that discussed above for the 1-tree, the Tetrahedral Lambda, the first six polygons enfolded in 10 Trees of Life and a pair of joined Type C triangles.

When Type B, both sets of seven polygons contain 500 (=50×10) geometrical elements that are unshared with the polyhedron, showing how they are prescribed by ELOHIM, the Godname of Binah with number value 50.

The 15 polygons encode the Cosmic Tree of Life (see pp. 13-14 of Article 44 and pp. 22-27 of Article 49). They also encode the root structure of the symmetry group E₈×E₈ used in heterotic superstring theory (see pp. 14-15 of Article 44 and #14 here).

<< Previous    1...   15  16  [17]  18  19  ...81    Next >>

Home