#16 Correspondence between the Tetrahedral Lambda, the first 6 polygons enfolded in 10 overlapping Trees of Life and the 1-tree 

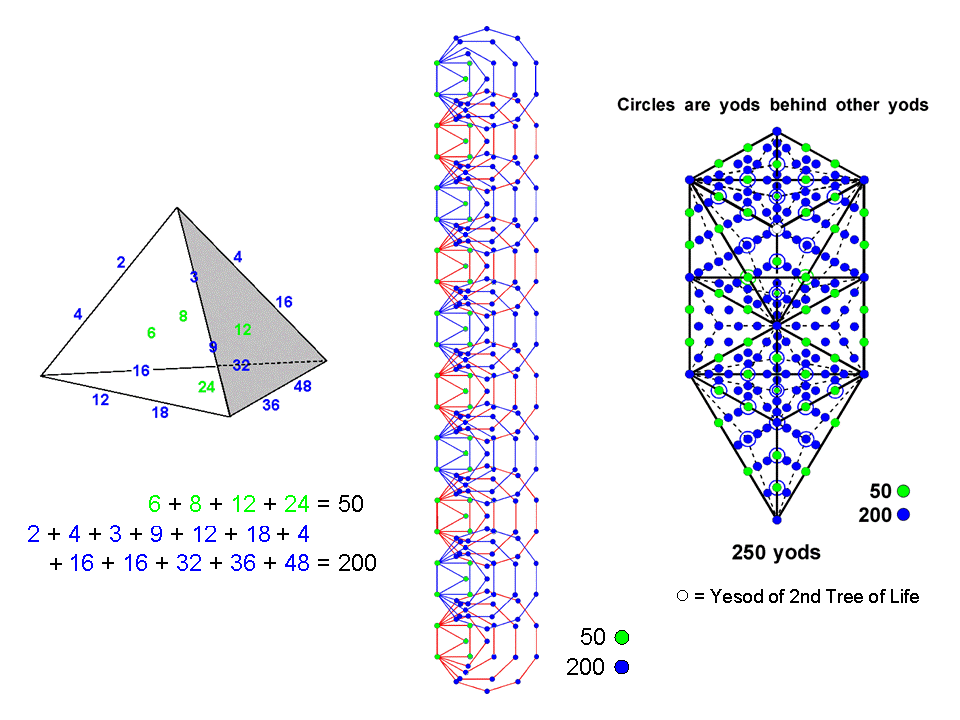
The sum of the 20 integers belonging to the Tetrahedral Lambda is 350. The sum of the integers at its vertices is 100. The sum of the integers at the centres of its four faces is 50, which is the number value of ELOHIM, the Godname of Binah. The sum of the 12 integers on its six edges other than those at its four vertices is 200.

Compare this with the inner form of 10 overlapping Trees of Life. The first six polygons enfolded in one Tree of Life have 26 corners, where 26 is the number value of YAHWEH, the Godname of Chokmah. The highest corner of the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher Tree. Therefore, 25 corners are intrinsic to each set of six enfolded polygons. The 60 polygons of the first six types enfolded in 10 overlapping Trees have 250 corners (shown in the diagram as blue & green yods) that are intrinsic to them, the highest corner of the hexagon enfolded in the tenth Tree being a point shared with the lowest corner of the hexagon enfolded in the eleventh Tree (it is shown as a bare corner without a blue yod). The 10 triangles and 10 squares have 50 corners and the 40 other polygons of the first six types have (250–50=200) corners. The former correspond to the sum (50) of the integers at the centres of the faces of the Tetrahedral Lambda and the latter correspond to the sum of the 12 integers on its edges other than those at its vertices. The 10 hexagons and the 10 pentagons also have 50 corners, and so the selection of the triangles and squares as corresponding to the sum 50 needs justification. This is provided by the 1-tree, which is discussed next.

The 1-tree has 251 yods when its 19 triangles are Type A triangles. Daath of the 1-tree becomes Yesod of the second Tree and so the white yod that denotes it in the diagram is the only yod that is not an SL of the 1-tree but an SL of the next higher Tree. It has to correspond to the topmost corner of the hexagon enfolded in the tenth Tree, which is shared with the hexagon enfolded in the next higher Tree; in each case the yod is not intrinsic to the lowest 10 Trees or the 1-tree. The 250 yods that are intrinsic to the 1-tree comprise 50 green hexagonal yods on its 25 Paths and 200 blue yods. The (10+1) top and bottom corners of the hexagons have to correspond to the (10+1) SLs of the 1-tree because Daath corresponds to the topmost corner of the hexagon in the tenth Tree. As SLs are denoted by blue yods, this means that the corners of the hexagons have to denoted by blue yods. The sum of the integers at the centres of the faces of the Tetrahedral Lambda is:

6 + 8 + 12 + 24 = (6 + 24) + (8 + 12) = 30 + 20 = 50.

This 30:20 split in the sum 50 is naturally reproduced in the geometry of the polygons by the 30 corners of the triangles and the 20 remaining corners of the squares. If the sum corresponded to the 50 corners of the pentagons, this would require the 20 endpoints of their root edges to correspond to the sum of the integers on the second and third faces, which seems, intuitively speaking, to be wrong, as these endpoints represent the start and end of the generation of each set of polygons, whilst these faces are intermediate stages in the generation of the Tetrahedral Lambda. The same conclusion would apply to the hexagons. Hence, the 'correct' correspondence is with the triangles and squares.

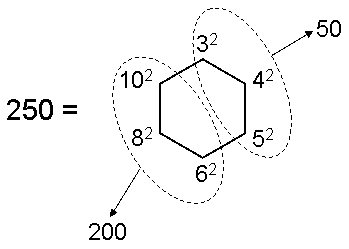
The squares of the numbers of corners of the first six polygons making up the inner form of the Tree of Life add up to 250:

This is amazing in itself, given that the 60 polygons of these types enfolded in 10 overlapping Trees of Life have 250 intrinsic corners. What is more remarkable still is that the sum of the first three squares 3², 4² & 5² is 50 and that the sum of the last three squares 6², 8² & 10² is 200. In other words, the distinction between the four integers at the centre of the Tetrahedral Lambda and the 12 integers on its edges between its vertices corresponds to the division of the first six polygons into the first three polygons and the last three polygons. Such simple correlation and harmony of number and geometry cannot be the result of coincidence. Instead, it is a clear manifestation of a universal, coherent design shared by sacred geometries such as the inner form of the Tree of Life and the 1-tree.

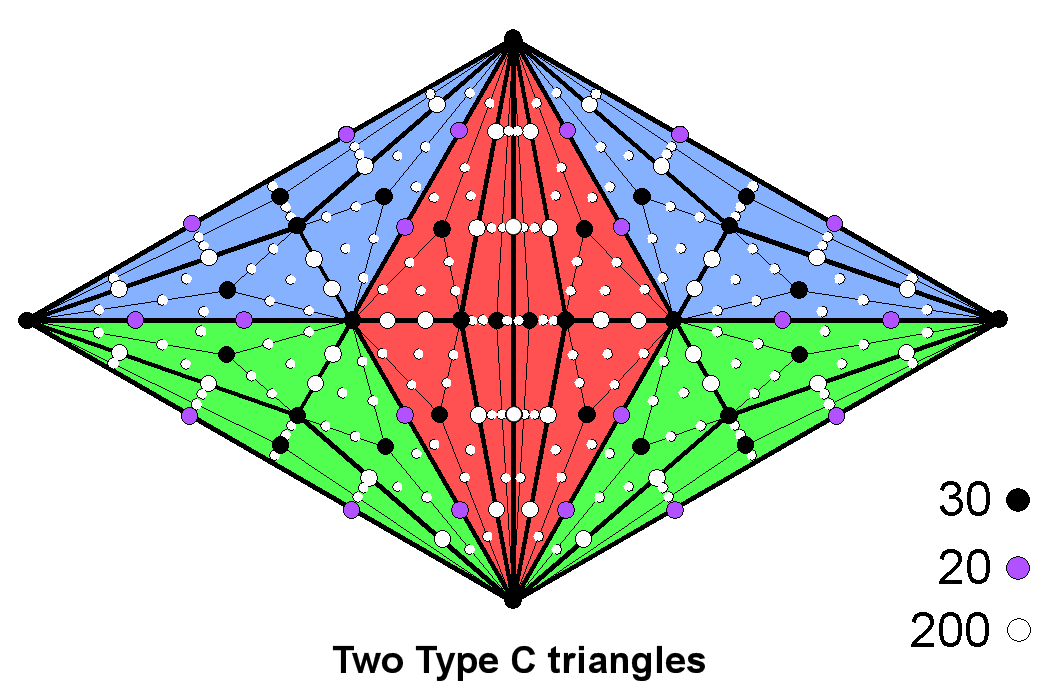
A Type C triangle has 127 yods. The two triangles in the inner form of the Tree of Life have 250 yods when they are both Type C. They comprise 30 black yods that are corners of the 54 tetractyses, 20 purple hexagonal yods outside their shared root edge on the sides of the sectors of each triangle and 200 white hexagonal yods. The two Type C triangles display the same 30:20:200 pattern as that displayed by the 16 integers in the Tetrahedral Lambda other than those at its vertices, by the 250 corners of the first six polygons enfolded in 10 Trees of Life and by the 250 yods in the 1-tree!

 
The reason for this correspondence is that the Type C triangle is the fourth stage of the Pythagorean differentiation of a triangle:

tetractys → Type A triangle → Type B triangle → Type C triangle

and therefore, according to the Tetrad Principle formulated in Article 1, it will embody numbers that are parameters of holistic systems, such as the three mentioned above (note: not only the same global parameters but also the pattern of their breakdown into other parameters). Confirmation of this is how the two Type C triangles embody the 248 roots of E₈, the gauge symmetry group describing the unified force between E₈×E₈ heterotic superstrings of ordinary matter. This is discussed in the section Superstrings as sacred geometry/Tree of Life. 248 is a parameter of holistic systems, being the number value of Raziel, the Archangel of Chokmah.

<< Previous    1...   14  15  [16]  17  18  ...81    Next >>

Home