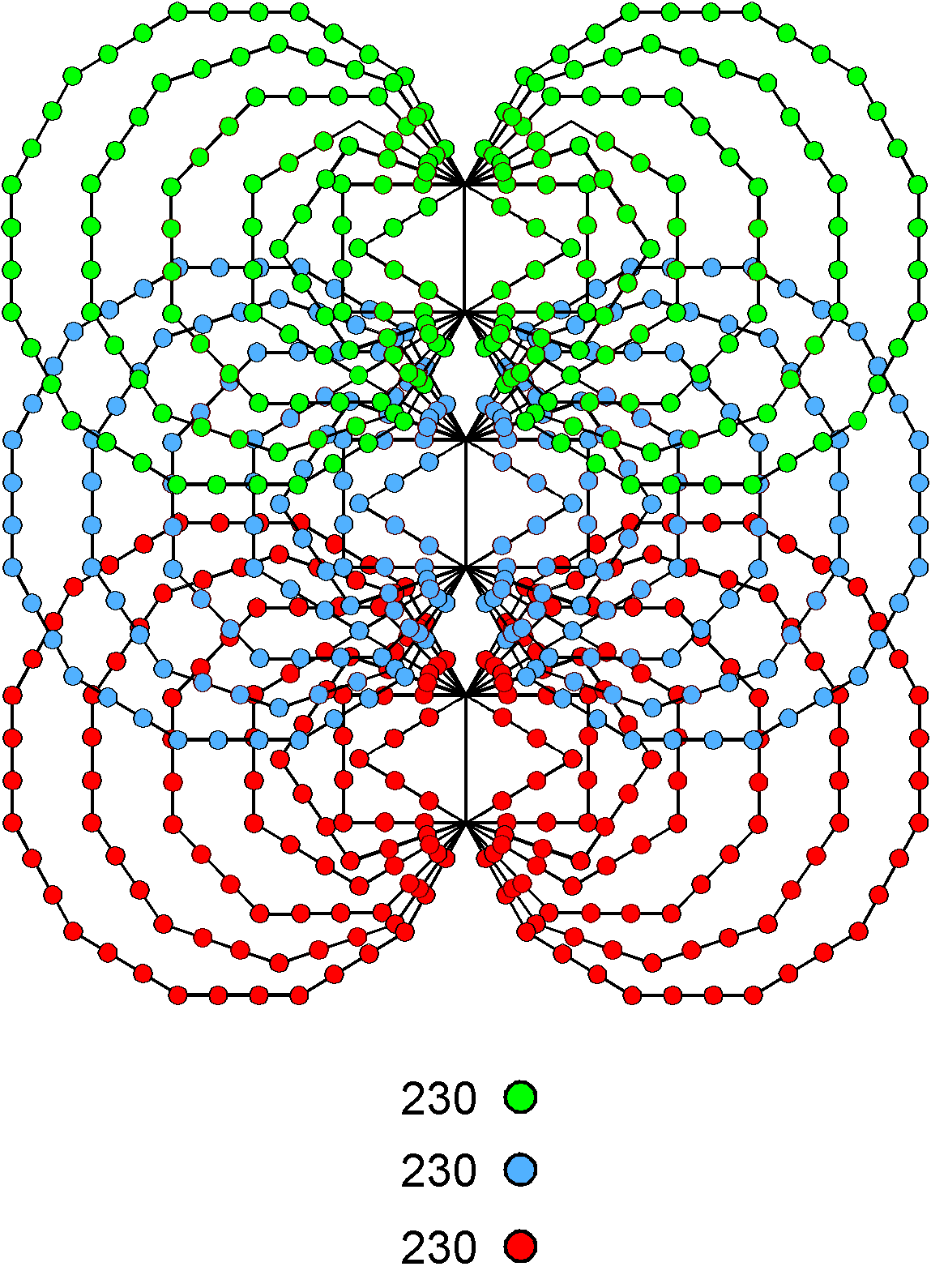
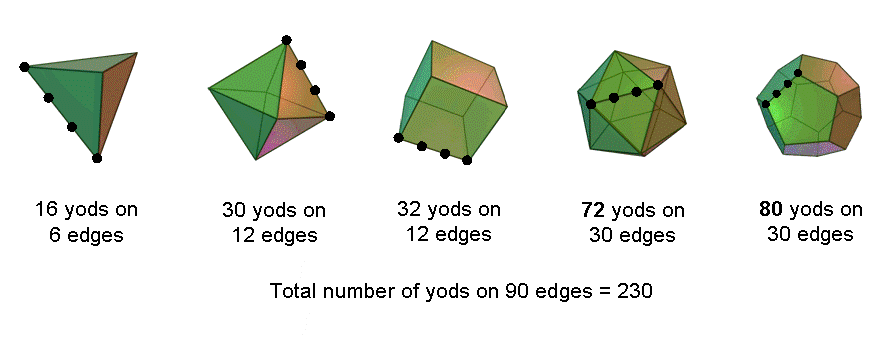
230 yods per set of (7+7) polygons lie on their sides. This is the number of yods lining the 90 edges of the five Platonic solids.
| << Previous 1... 12 13 [14] 15 16 ...81 Next >> |
#14 Correspondence between the five Platonic solids, the inner Tree of Life and the disdyakis triacontahedron
We saw in #6 that 232 yods lie on the sides of the 14 enfolded polygons of the inner Tree of Life outside their root edge. They shape its form. In each overlapping Tree of Life, there are a similar set of polygons. The topmost corners of the two hexagons in each set coincide with the lowest corners of the two hexagons enfolded in the next higher Tree of Life. This means that 230 yods on sides of the 14 polygons enfolded in each Tree of Life are intrinsic to that set of polygons. Three sets of enfolded polygons are shown below, one set with 230 red boundary yods that are intrinsic to it, the next higher set with 230 blue boundary yods and the third set with 230 green yods on sides of polygons.
 |
|
|
230 yods per set of (7+7) polygons lie on their sides. This is the number of yods lining the 90 edges of the five Platonic solids. |
|
When they are constructed from tetractyses, each of the 90 edges of the five Platonic
solids is lined by four yods (two vertices and two hexagonal yods). (90×2=180) hexagonal yods and
50 vertices, i.e., 230 yods, line their edges. Just as the number 230 measures the
2-dimensional shapes of each set of 14 enfolded polygons, so it determines the 3-dimensional
shapes of the five regular polyhedra! Remarkable though it be, the reason for the appearance in both
geometries of the same number with similar functions is simple: the five Platonic solids are the regular,
polyhedral counterpart of the inner form of the Tree of Life; they constitute sacred geometry. This
is a remarkable illustration of the correspondences that exist between different manifestations of holistic
systems.

When the vertical axis of the disdyakis triacontahedron with 62 vertices passes through two
diametrically opposite A vertices, the 60 vertices between the latter are the corners of seven polygons arranged in
parallel sheets (see here). The fourth (central) polygon has 12 corners and 12 sides that
are polyhedral edges. Hence, as the polyhedron has 180 edges, (180–12=168) edges are above and
below this polygon, that is, 84 edges are above it. (62–12=50) vertices are
above and below it, that is, 25 vertices are above it. Hence, half of the polyhedron down to its midplane has
(25+12=37) vertices and (84+12=96) edges. When its faces are constructed from tetractyses, there are two
hexagonal yods and two vertices on each edge. Hence, (96×2 + 37 = 229) yods line the edges in half the
polyhedron. This is the remarkable way in which ELOHIM, the Godname of Binah with number value
50, prescribes the form of the disdyakis triacontahedron as part of the Polyhedral Tree of Life,
because 229 is the 50th prime number. There are 230 yods either at its centre or on the edges
of half the polyhedron. They correspond to the 230 yods lining the edges of the five Platonic solids and to the
230 yods that are intrinsic to the inner form of each overlapping Tree of Life. In all three cases, the number
230 determines the shape of the object(s) possessing sacred geometry.