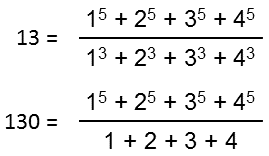 The outer Tree of Life (עץ חיים)
The outer Tree of Life (עץ חיים)
The 7 enfolded polygons in half of the inner Tree of Life. The black line is the root edge and the black dashed line is the only part of their geometry that is shared with the outer Tree of Life.
1. The outer & inner Trees of Life
The outer Tree of Life
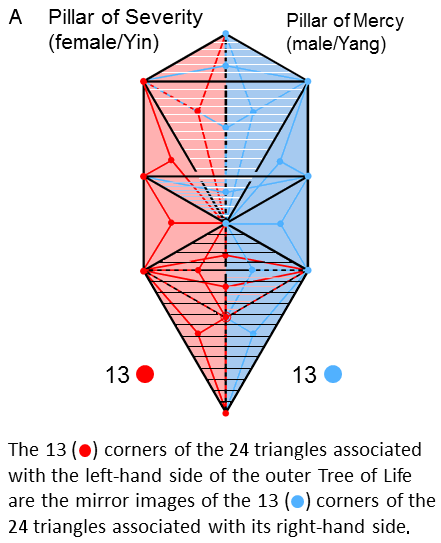
The outer Tree of Life is composed of
16 triangles with 10 corners & 22 sides (black lines). Because of its mirror symmetry, every
point, line & triangle in either half has its counterpart in the opposite half reflected across
the central axis defined by the Pillar of Equilibrium. The right-hand side of the outer Tree of
Life is composed of 3 blue corners, 7 black sides & 6 blue triangles; likewise, the left-hand
side comprises 3 red corners, 7 black sides & 6 red triangles. Four corners (2 red, 2 blue)
& 3 horizontal black sides of 6 triangles span both sides. Three of these
triangles with 2 blue corners aligned with the central axis can be associated with the right-hand
side; 3 triangles with 2 red corners aligned with the central axis can be associated with the
left-hand side. The 16 triangles can be divided into two sets of 8 triangles, each consisting of 5
triangles which do not span the central Pillar of Equilibrium and 3 which do. The latter comprise 2
triangles (one upward-pointing, the other downward-pointing) that form the kite-shaped Upper or
Lower Faces (these are shaded with, respectively, white and black lines); this leaves two
triangles: Chesed-Geburah-Tiphareth & Netzach-Hod-Yesod. The former belongs to the right-hand
set of triangles (this is indicated by the horizontal blue lines in its left-hand side). The latter
belongs to the left-hand set of triangles, as shown by the light red lines in its right-hand side.
Suppose that a geometrical object is composed of a corners & b sides of c triangles. Its
geometrical composition can be written as (a,b,c). The geometrical composition of each "half" of
the outer Tree of Life is (5,11,8). When all triangles are Type A, 8 corners & (8×3=24) blue or
red sides of (8×3=24) triangles are added to each half, which now has the composition: (13,35,24),
i.e., 72 geometrical elements. The outer Tree of Life has 144 geometrical
elements with the composition: (26,70,48).
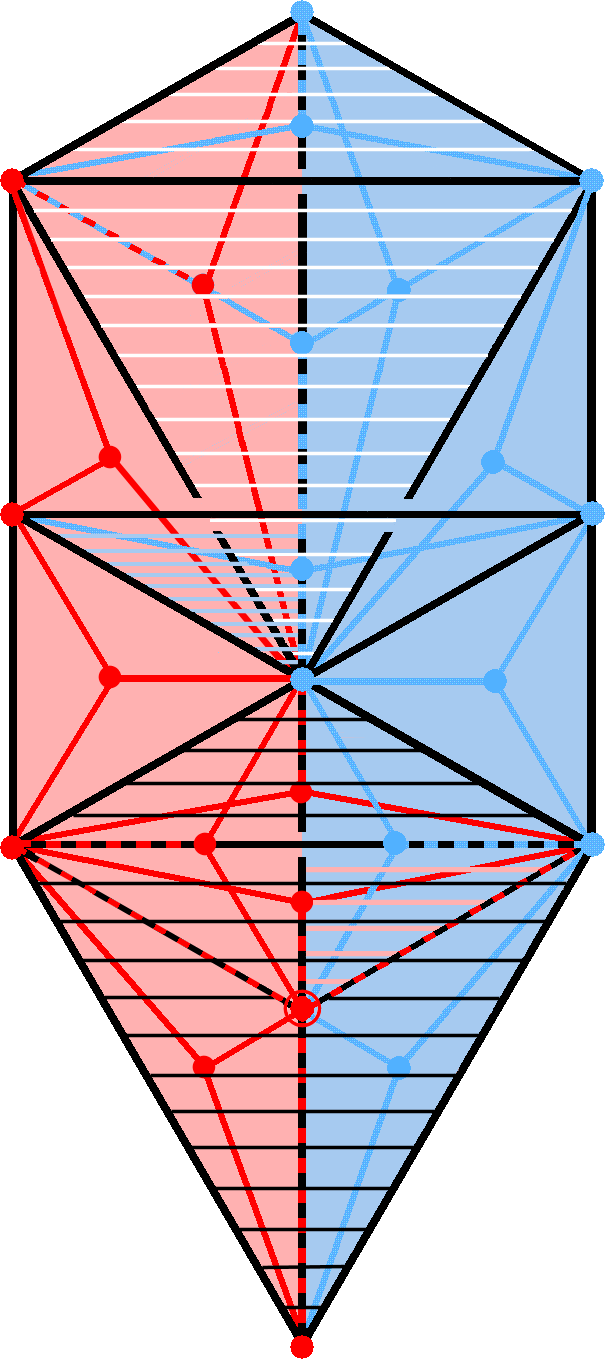
The inner Tree of Life
Each half of the inner Tree of Life consists of 7
enfolded polygons:
triangle-square-pentagon-hexagon-octagon-decagon-dodecagon.
Divided into their 47 sectors, they have the composition: (41,88,47), i.e., 176 geometrical elements. The top and lowest corners of the hexagon and its centre (black dots) and the two vertical, dashed black lines are shared with the outer Tree of Life as its Pillar of Mercy. The composition of the unshared part is (38,86,47). The composition of its unshared part outside its root edge (black line) is (36,85,47), i.e., 168 geometrical elements. This is how the superstring structural parameters 168/1680 determined with micro-psi by C.W. Leadbeater over a century ago is embodied in the geometry of the inner Tree of Life.
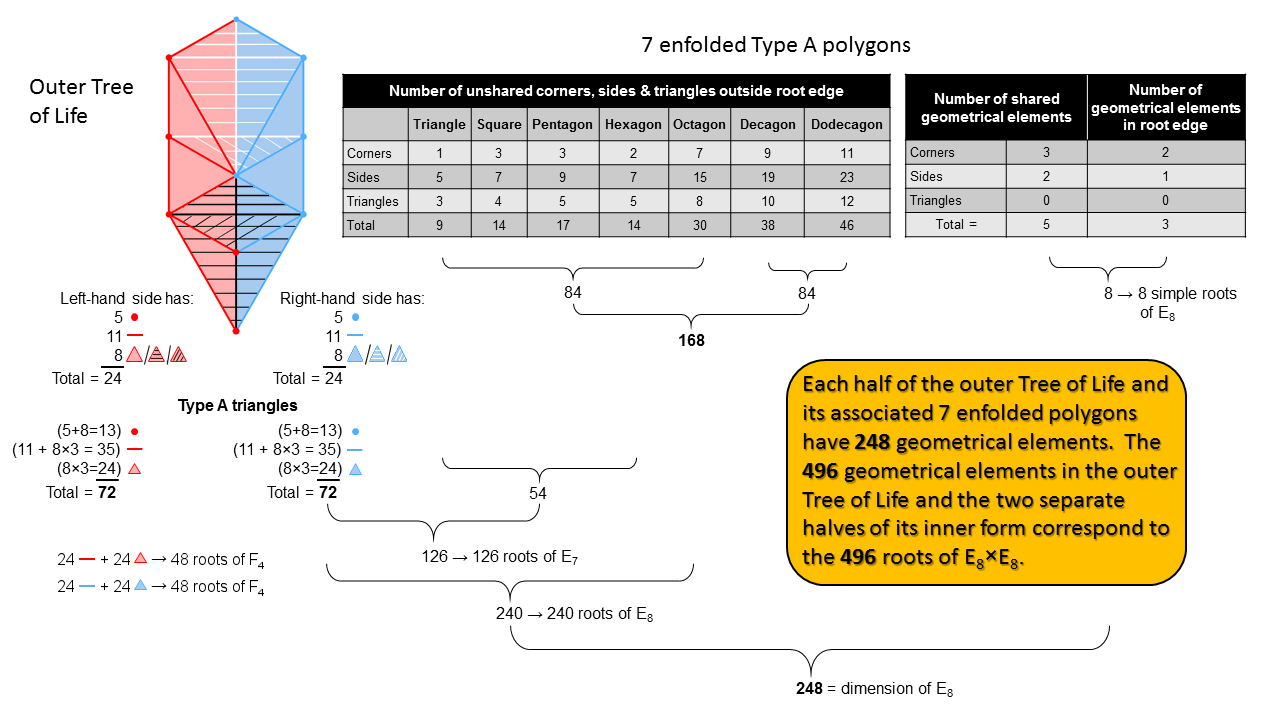
2. 496 geometrical elements make up the outer & inner Trees of Life
The number of corners, sides & triangles in a Type A n-gon = 4n + 1. (4n−2) geometrical elements are outside the side it shares with other enfolded polygons. The right-hand corner of the enfolded triangle coincides with Chesed of the outer Tree of Life and the top and bottom corners of the enfolded hexagon coincide with, respectively, Chokmah and Binah, whilst the two interior, vertical sides of its sectors coincide with the Chokmah-Chesed Path and the Chesed-Netzach Path. The table lists the geometrical elements in each of the 7 polygons outside the shared root edge that are unshared with triangles in the outer Tree of Life. The first 5 polygons have 84 geometrical elements, as do the last 2 polygons. This 84:84 division in the 168 unshared geometrical elements is characteristic of holistic systems (for example, see Article 64). The two internal sides of the hexagon shared with the outer Tree comprise 3 corners & 2 sides, whilst the root edge comprises 2 corners & one side. The composition of shared/root edge elements is (5,3,0). We found above that the composition of the 72 elements in each half of the outer Tree of Life is (13,35,24). The composition of the outer Tree of Life and 2 separate halves of the inner Tree of Life is
(176+72) + (72+176) = 248 + 248 = 496
= (41,88,47) + ((13,35,24) + (13,35,24) + (41,88,47)
= (54,123,71) + (54,123,71) = (108,246,142).
248 is the dimension of the rank-8 exceptional Lie group E8 and 496 is the dimension of E8×E8. This is one of the two symmetry group found in 1984 to be free of quantum anomalies, a discovery that ushered the so-called "first superstring revolution" in theoretical physics. Every one of the 496 geometrical elements in the outer and inner Trees of Life corresponds to a root of E8×E8. The 248 geometrical elements in either half of the outer Tree and its associated set of 7 enfolded polygons correspond to the 248 roots of E8. The 8 shared elements correspond to its 8 simple roots and the (72+168=240) elements correspond to its 240 roots. They have the composition (49,120,71), i.e., they comprise 120 corners & triangles and 120 sides.
The first 4 enfolded polygons have 54 unshared geometrical elements outside their root edge with the composition (9,28,17). Hence, there are (72+54=126) elements belonging either to each half of the outer Tree of Life and the first 4 enfolded polygons belonging to its associated set of 7 polygons. They correspond to the 126 roots of E7, the largest exceptional subgroup of E8 (for more details, see the discussion in (5) about E7).
The 72 geometrical elements in each half of the outer Tree of Life correspond to the 72 roots of E6, another exceptional subgroup of E8, because the 126 elements corresponding to the 126 roots of E7 contain the 72 elements, which is consistent with E6 being a subgroup of E7.
When the original (8+8=16) triangles are divided into their (24+24=48) sectors, (24+24=48) sides are added. The 48 sides & triangles in each half of the outer Tree of Life are the counterpart of the 48 roots of F4, the rank-4 exceptional subgroup of E6 (see the discussion below about F4).

E8 Coxeter
projection of the 240 vertices of the 421 polytope.
3. Correspondence between the geometrical
composition
of the Tree of Life and the roots of
E8×E8
Whilst studying and classifying the regular and semi-regular polytopes (higher-dimensional versions of the 3-d polyhedra), the English amateur mathematician Thorold Gosset (1869-1962) discovered in 1900 the 421 polytope, a semi-regular 8-polytope. The position vectors of its 240 vertices in 8-d space are the root vectors of the 240 roots of E8. Its Petrie polygon is the triacontagon, a regular polygon with 30 corners. The E8 Coxeter plane projection of the 421 polytope consists of 8 concentric triacontagons.
Each half of the outer Tree of Life comprises 8 triangles with 5 corners and 11 sides. When they are Type A, they consist of (8×3=24) sectors with (5+8=13) corners and (11 + 8×3 = 35) sides — a total of 72 geometrical elements.
The 7 enfolded Type A polygons comprise 41 corners and 88 sides of 47 sectors. Five of these 176 geometrical elements (3 corners & two sides of sectors of the hexagon) are shared with two triangles whose bases are either the left-hand or the right-hand Pillars of the outer Tree of Life. Therefore, (176−8=168) geometrical elements outside their root edge belong exclusively to each set of 7 enfolded polygons. They are intrinsic to them.
Two separate sets of 7 enfolded polygons
Each half of the outer Tree of Life and its associated separate set of 7 enfolded polygons have
(72+168=240) geometrical elements outside their root edge. They
correspond to the 240 roots of E8. The 8 additional geometrical elements either shared
with the outer Tree or in the root edge of each set of polygons correspond to the 8 simple roots of
E8. In total, the outer & two separate halves of the inner Trees of Life have
(8+240+8+240=496) geometrical elements that correspond to the
496 roots of E8×E8.
Two combined sets of 7 enfolded polygons
Instead of 496 geometrical elements, the outer & inner Trees now have
(240+240=480) geometrical elements outside the root edge, of which 144 belong to the former and
(168+168=336) are intrinsic to the latter. These 480 elements correspond to the
480 roots of E8×E8.
E8
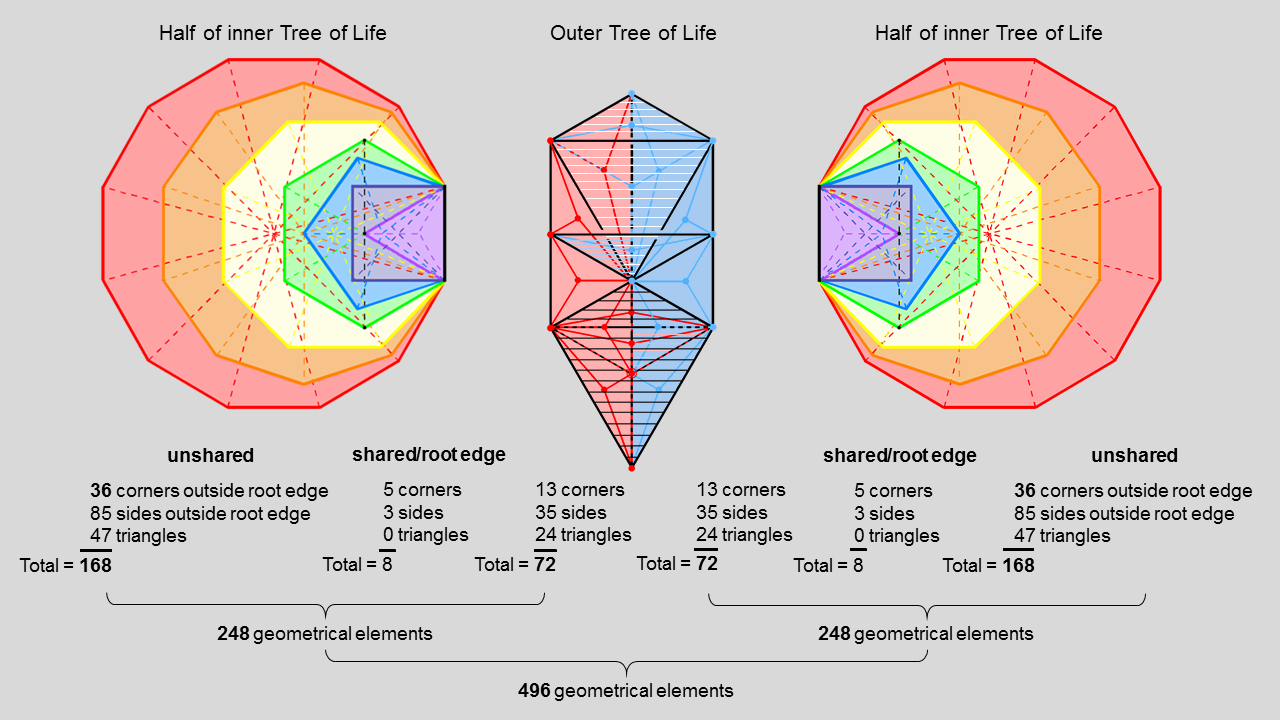
4. Correspondence between the 168 unshared
geometrical
elements and the 168 roots of E8 that are not roots of E6
The outer Tree of Life with 16 Type A triangles consists of 48 triangles with 26 corners & 70 sides. Seventy-two of these 144 geometrical elements can be associated with each "half" of the outer Tree of Life.
Each set of 7 enfolded Type A polygons contains 176 geometrical elements. Three corners of triangles and two sides (coloured green in the diagram opposite) in each side pillar of the outer Tree of Life coincide, respectively, with the topmost, centre & bottom of a hexagon and the two internal vertical sides of its sectors. This means that 67 of the 72 geometrical elements in each half of the outer Tree are intrinsic to it, where 67 is the number value of Binah. (176−5−3=168) geometrical elements outside the root edge are intrinsic to each set of 7 enfolded polygons.
The number of geometrical elements in the separate outer and inner Trees of Life = 176 + 144 + 176 = 496. Each half has (72+168+8=248) geometrical elements. This is the dimension of E8. The 496 geometrical elements correspond to the 496 roots of E8×E8′. The 8 geometrical elements that are either shared or belong to the root edge correspond to its 8 simple roots. The 72 elements in each half of the outer Tree of Life correspond to the 72 roots of E6, the rank-6 exceptional subgroup of E8. The 168 elements that are intrinsic to each set of 7 enfolded polygons correspond to the 168 roots of E8 or E8′ that are not roots of E6 (in the latter case, it is written E6′ in the diagram). Here is unambiguous evidence that the geometrical composition of the outer & inner Trees of Life is analogous to the root composition of E8×E8 rather than to SO(32) — the only other gauge symmetry group which, because it has the crucial dimension 496, is free of quantum anomalies.
The composition of the 240 geometrical elements outside the root edge in each half of the combined outer & inner Trees of Life is (49,120,71). EL CHAI, the Godname of Yesod with number value 49, prescribes the number of corners of the 71 triangles in each half of the combination. ELOHA, the Godname of Geburah with number value 36, prescribes the 36 corners of the 47 triangles in each set of 7 enfolded polygons that are outside their root edge and unshared with the outer Tree of Life.
E7
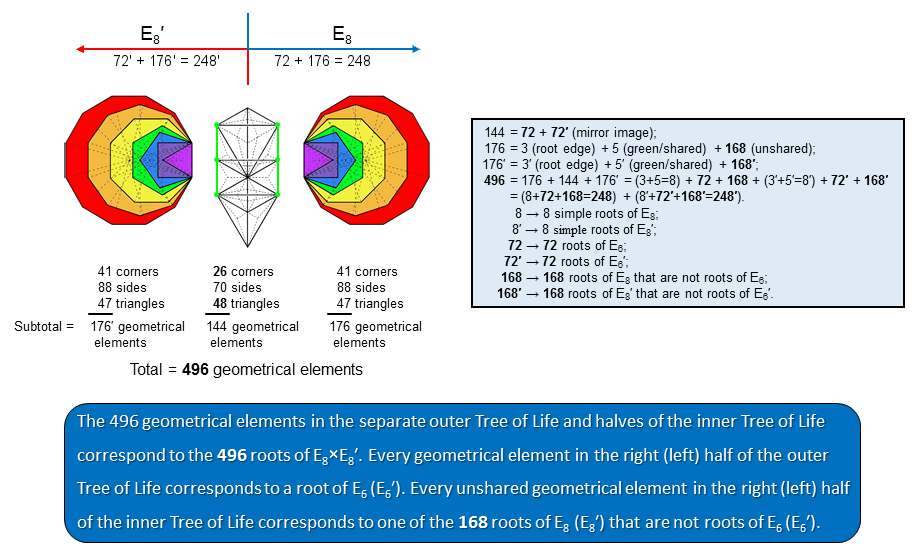
5. Tree of Life counterpart of the 126 roots of E7
In 7-dimensional geometry, 231 is a uniform polytope, constructed from the E7 group. Its Petrie polygon is the octodecagon. Its 126 vertices represent the 126 root vectors of the simple, exceptional Lie group E7. These 126 roots have as follows their counterparts in the outer & inner Trees of Life:
the first 4 polygons are the triangle, square, pentagon & hexagon. Article 48 analyses the holistic nature of this subset of the 7 regular polygons making up the inner form of the Tree of Life. The diagram in (2) shows that they have 54 unshared geometrical elements outside their shared root edge. Hence, each half of the outer Tree of Life and its associated set of the first 4 enfolded polygons have (72+54=126) geometrical elements. They correspond to the 126 roots of E7, the largest exceptional subgroup of E8.
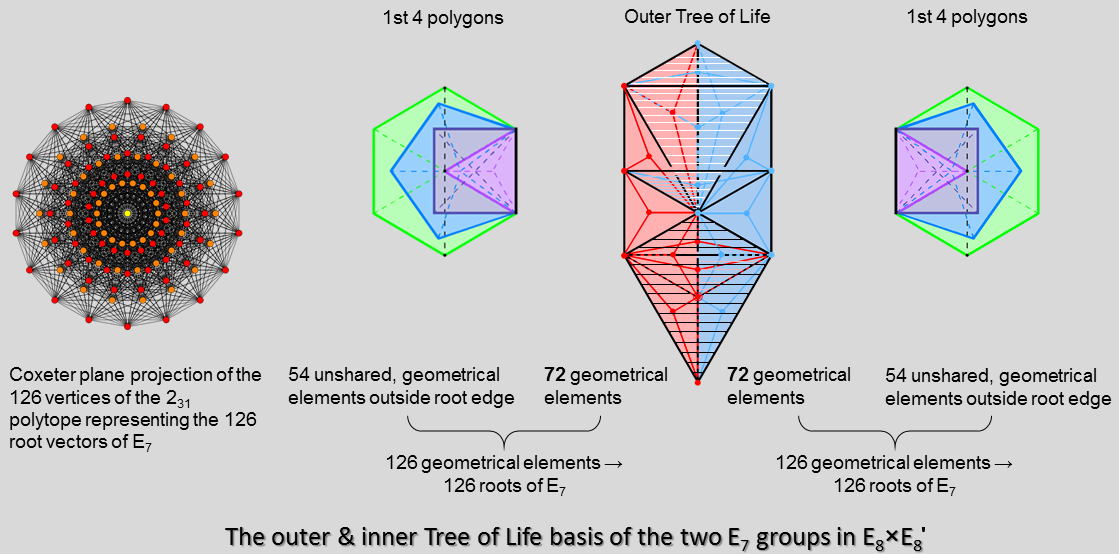
6. Outer Tree of Life basis of the 72 roots of E6
The I22 polytope is a 6-d uniform polytope with 72 vertices. Its Petrie polygon is the dodecagon. Its vertices represent the 72 roots of the rank-6 exceptional group E6, which is an exceptional subgroup of E7 & E8.
Each half of the outer Tree of Life has 8 triangles with 5 corners & 11 sides. When they are Type A, their (8×3=24) sectors have (5+8=13) corners & (11 + 8×3 = 35) sides. Each half has 72 geometrical elements. They comprise (13+11=24) corners and original sides, 24 new sides & 24 triangles.
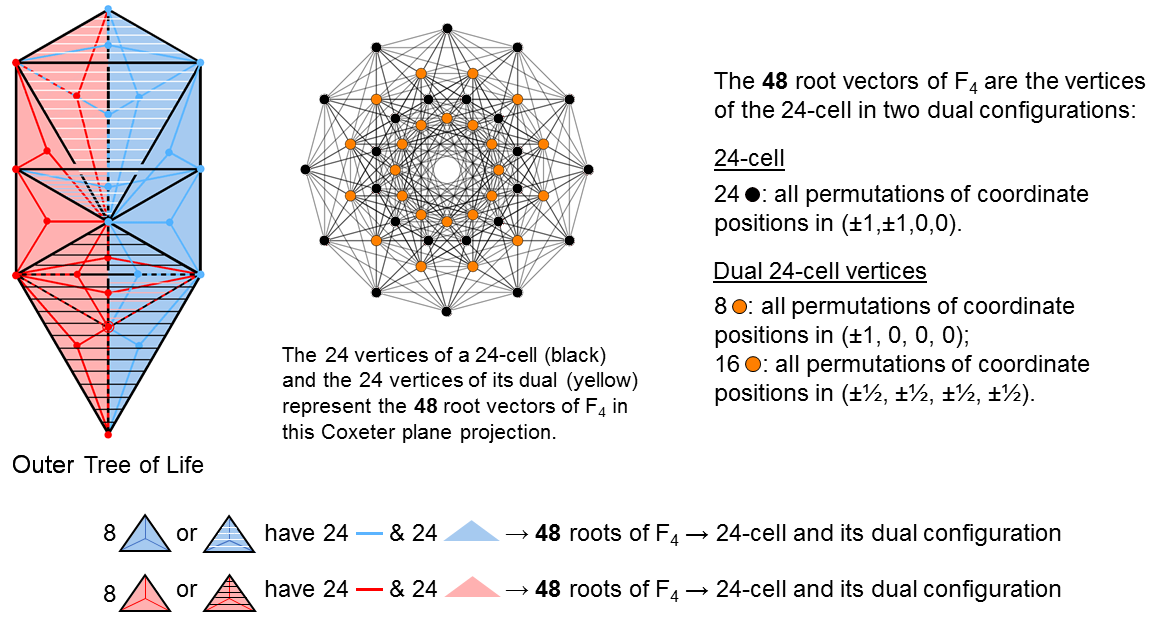
The outer Tree of Life basis of the two F4 groups in E8×E8′
7. Outer Tree of Life basis of the 48 roots of F4
E6 has a rank-4 exceptional subgroup called F4. It has 48 roots. The Coxeter plane projection of the 24 vertices of a 24-cell and the 24 vertices of its dual configuration are its 48 root vectors.
As found in (6),
the 72 geometrical elements in the 8 Type A triangles in each half of the outer
Tree of Life comprise 3 sets of 24 elements. As the 48 roots of
F4 coincide
with 2 sets of 24 vertices of 24-cells (see diagram), we expect their geometrical counterpart in
each half of the outer Tree of Life to comprise 2 sets of 24 geometrical elements. But which pairs
of 24 corners & original sides, 24 new sides and 24 triangles? An equivalent form of this
question is: which set of 24 geometrical elements (let us call it 24 and underline all numbers
representing sets of geometrical elements) corresponds to the 24 roots in
E6 that are not roots of F4? There are 3
possibilities:
1. 24 = (0,0,24).
As 72 =
(13,35,24), 48 =
72 − 24 = (13,35,0), where 35 = 11 + 24
(see (6)). Therefore, 48 = (13,11,0) + (0,24,0).
So, as required, it does consist of 2 sets of 24 geometrical elements.
As 168 = (36,85,47), the 192 roots of
E8 other than the 48 roots of
F4 have counterpart geometrical elements with the composition
(36,85,71). As a holistic parameter (e.g., the 192 Yang & Yin lines in
the 64 trigrams in each diagonal half of the 8×8 array of hexagrams), we
expect the number 192 to divide naturally into two sets of 96 (e.g., the 96 Yang lines and
the 96 Yin lines in each diagonal half). The deduced composition of the 192 geometrical
elements is inconsistent with this requirement. Therefore, 24 ≠ (0,0,24);
2. 24 =
(0,24,0).
As 72
= (13,35,24), 48 = (13,11,24) =
(13,11,0) + (0,0,24), i.e., it consists of 2 sets of 24 elements.
Then 192 = 24
+ 168 =
(36,109,47). This also fails to divide into 2 sets of 96 geometrical elements.
Therefore, 24 ≠ (0,24,0).
3. 24 =
(13,11,0).
As 72
= (13,35,24), 48 = (0,24,24), i.e.,
it divides into 2 sets of 24 elements. Then 192 = 24
+ 168 =
(49,96,47), i.e., it consists of (49+47=96) corners &
triangles and 96 sides. So, as required, it divides naturally into 2 sets of 96
geometrical elements. The composition 24 = (13,11,0) is the only one
of these three possibilities that satisfies both requirements. It means that
the 48 geometrical elements in each half of the outer Tree of Life
corresponding to the 48 roots of
F4 consist of the 24 new sides & 24 new triangles generated by the
transformation of the 8 triangles in each half into Type A triangles.
Just as the 480 8-dimensional root vectors of E8×E8′ have (8×480=3840=384×10) coordinates, so the 48 root vectors of F4 have (8×48=384) coordinates. E8×E8′ has (192+192=384) roots other than those in the F4 groups belonging to E8 and E8’. The appearance of the holistic parameters 192 & 384 (see here) in F4 and the fact that 48 is another holistic parameter indicate the central importance of this symmetry group for heterotic E8×E8′ superstrings as a step in the breakdown of their E8×E8′ & E8 symmetries.
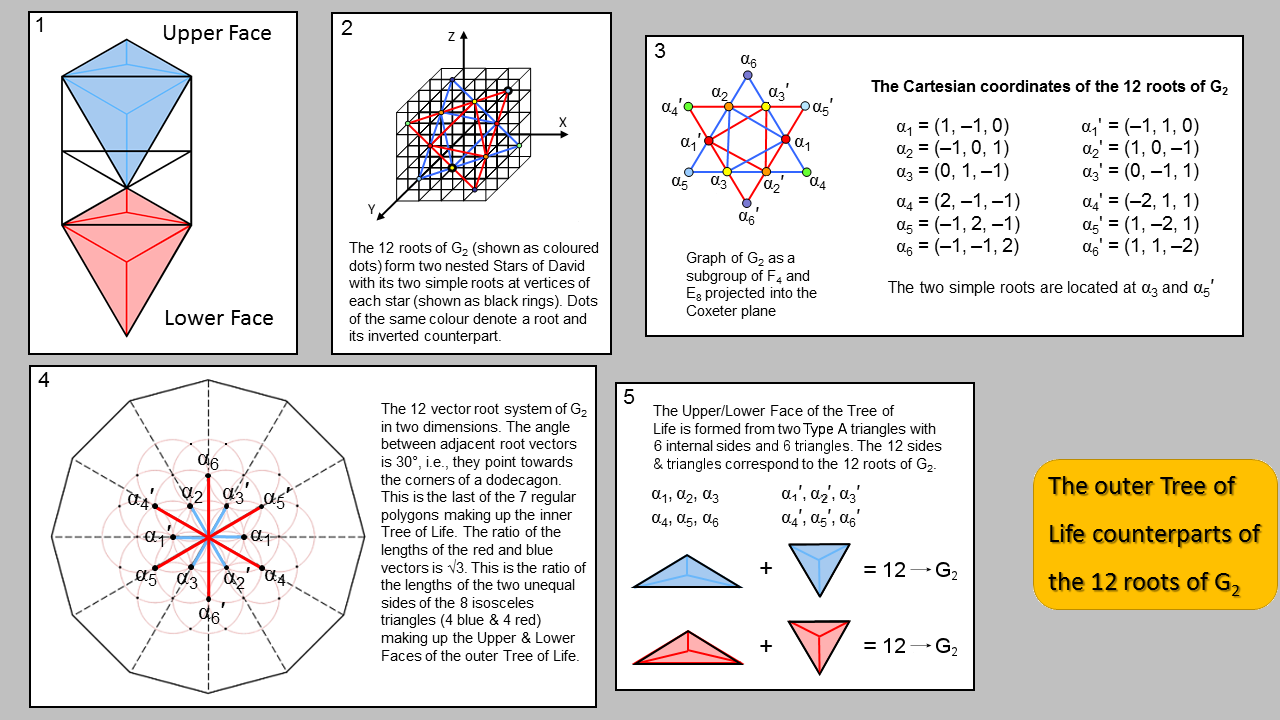
8. Outer Tree of Life basis of the 12 roots of G2
1. Three of the 8 Type A triangles associated with each half of the outer Tree of Life span the central Pillar of Equilibrium. Of those associated with its right-hand side, only the two blue Type A triangles (Kether-Chokmah-Binah & Binah-Chokmah-Tiphareth are shared with the next higher, overlapping Tree of Life because they form the Upper Face, which is the Lower Face of the next higher Tree. Similarly, of those associated with its left-hand side, only the two red Type A triangles (Tiphareth-Netzach-Hod & Hod-Netzach-Malkuth) are shared with the next lower Tree of Life because they form the Lower Face, which is the Upper Face of the next lower Tree. Inside the two shared blue Type A triangles are (2×3=6) sides and (2×3=6) triangles, i.e., 12 sides & triangles. Similarly for the two red Type A triangles. We found in (7) that, for either half of the outer Tree of Life, 48 = (0,24,24). Therefore, 48 = (0,6+18,6+18) = (0,6,6) + (0,18,18). The 12 sides & triangles in the former set correspond to the 12 roots of the smallest exceptional group G2, which is a subgroup of F4. The division:
48 = 12 sides & triangles + 36 sides & triangles
is another manifestation of the 12:36 division of the
48 corners of the 7 separate polygons forming each half of the inner Tree of
Life into the 12 corners of the dodecagon and the 36 corners of the first 6
polygons.
2. The 12 roots of G2, when projected into the Coxeter plane, are at the corners of
two nested Stars of David. Its two simple roots are located at two of these corners.
3. Roots of G2 at opposite corners of triangles are inversions of each other.
4. The root vectors of the 12 roots in 2 dimensions point towards the corners of a dodecagon
because they are all separated by the angle of 30°.
5. The (3+3=6) internal sides & sectors of one of the two blue triangles forming the Upper Face
correspond to 6 roots of G2 (namely, α1-α6). The 6 internal
sides & sectors of the other blue triangle correspond to their inversions (α1′-α6′). Similarly, the
6 internal sides & 6 sectors of the two red triangles in the Lower Face correspond to the
6 roots & their inversions for the G2 group belonging to the second group
E8′.
|
|
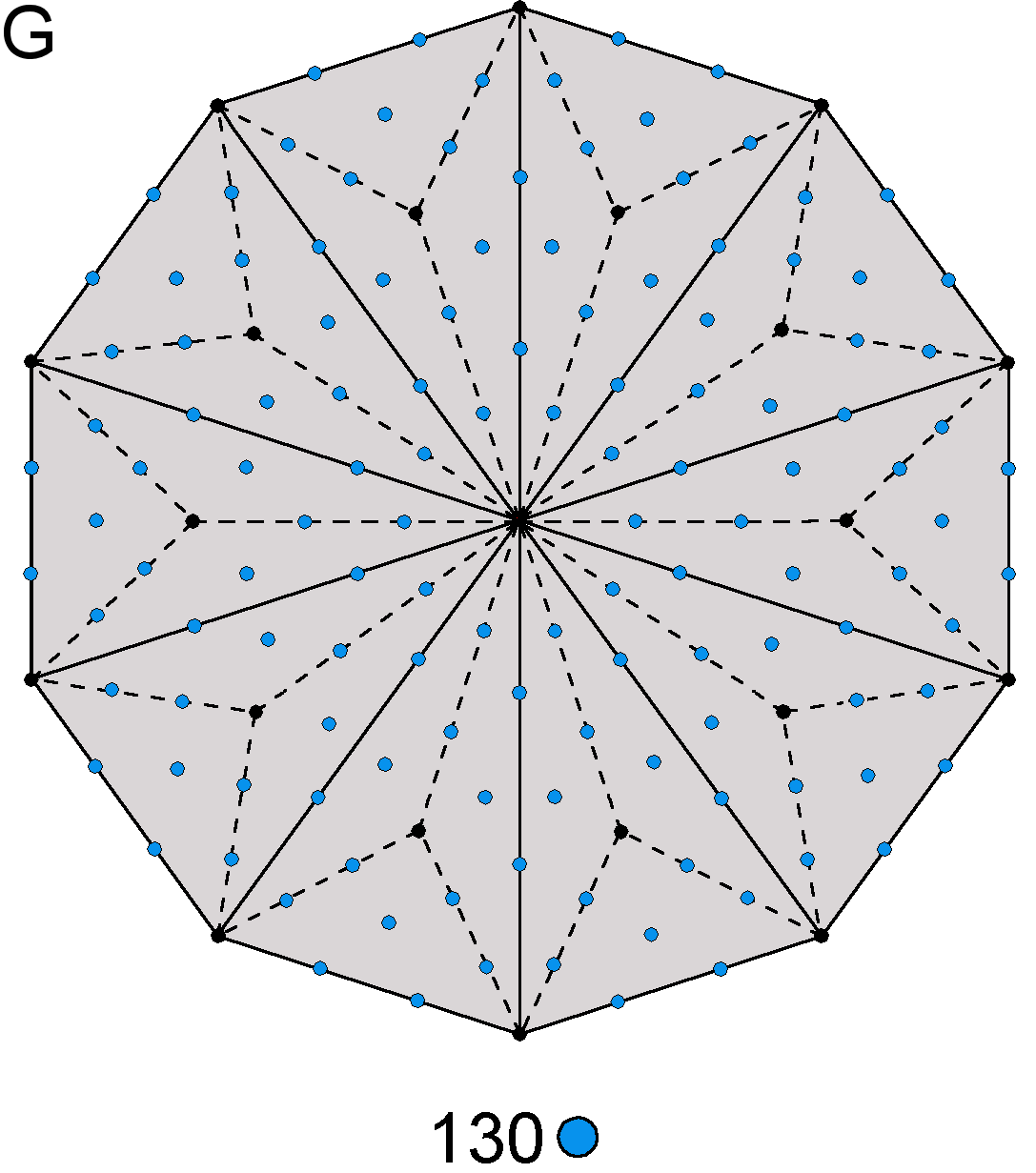
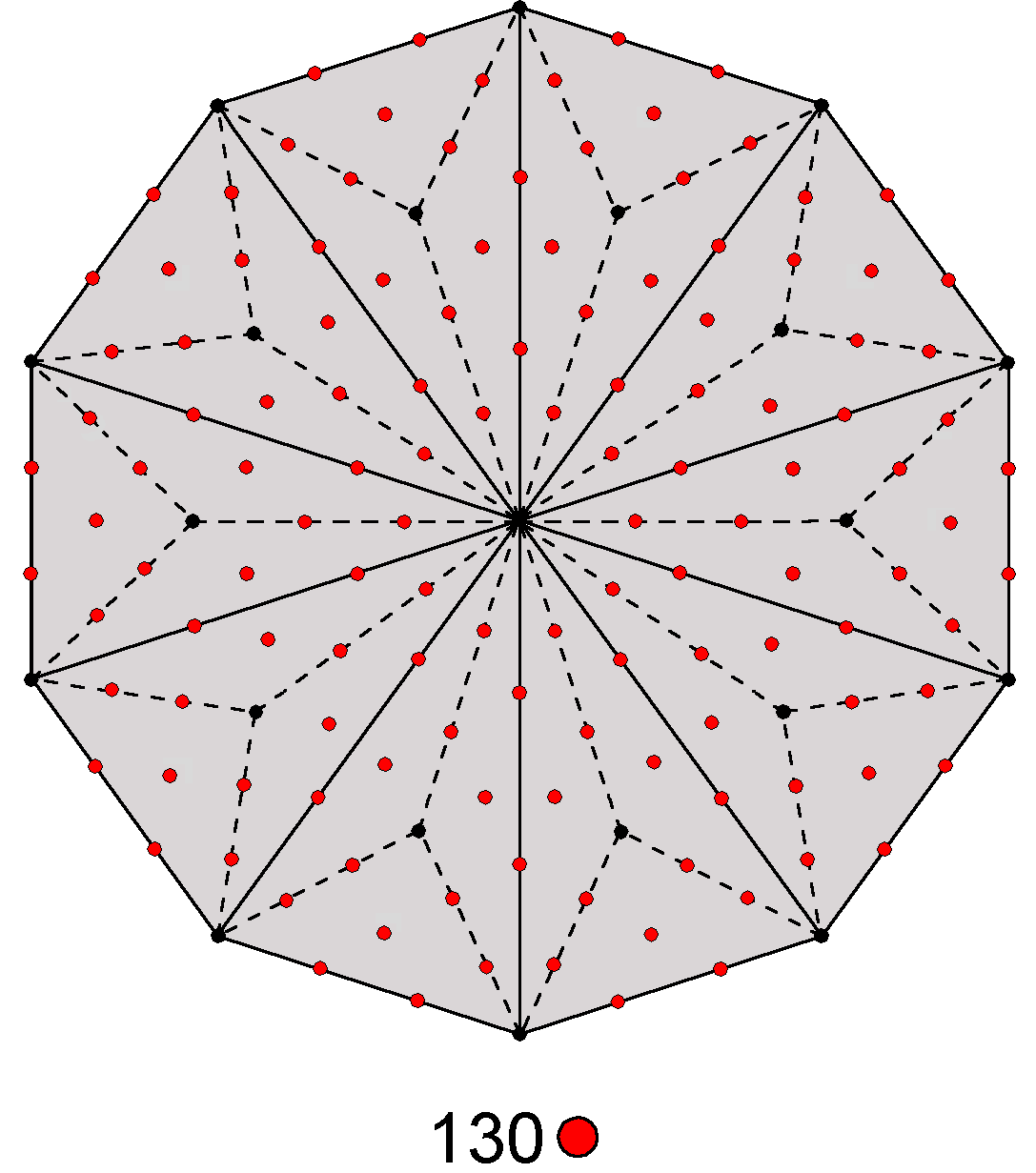
260 yods other than corners line tetractyses in the pair of Type B dodecagons.
|
|
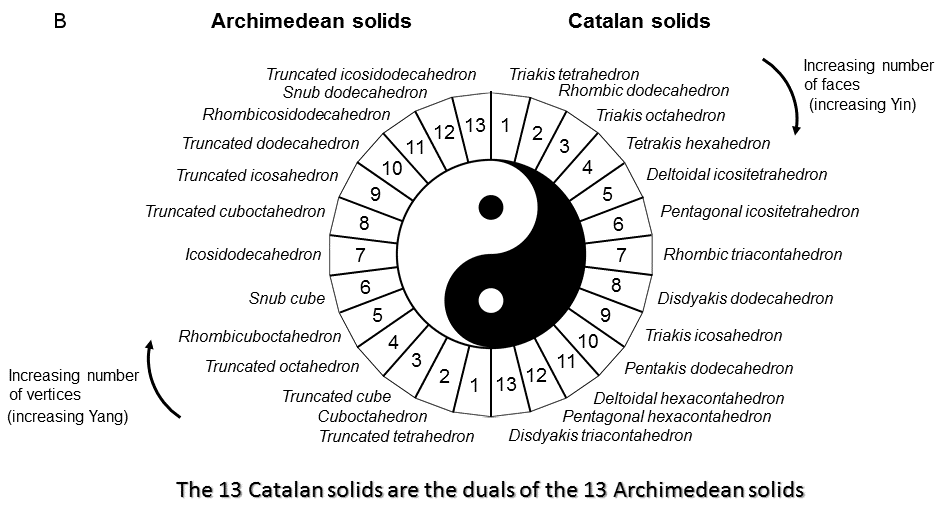
9. 13:13 division in the outer & inner Trees of Life, the Archimedean & Catalan solids and the types of intervals in the 7 diatonic musical scales A. When just simple triangles, the 16 triangles in the outer Tree of Life have 10 corners. When Type A, they have 48 sectors that meet at 16 internal corners. Their (10+16=26) corners are prescribed by YAHWEH, the Godname of Chokmah with number value 26. Its letter values quantify the numbers of different types of corners: YHVH = 26 Y = 10 → 10 corners locating the 10 Sephiroth;
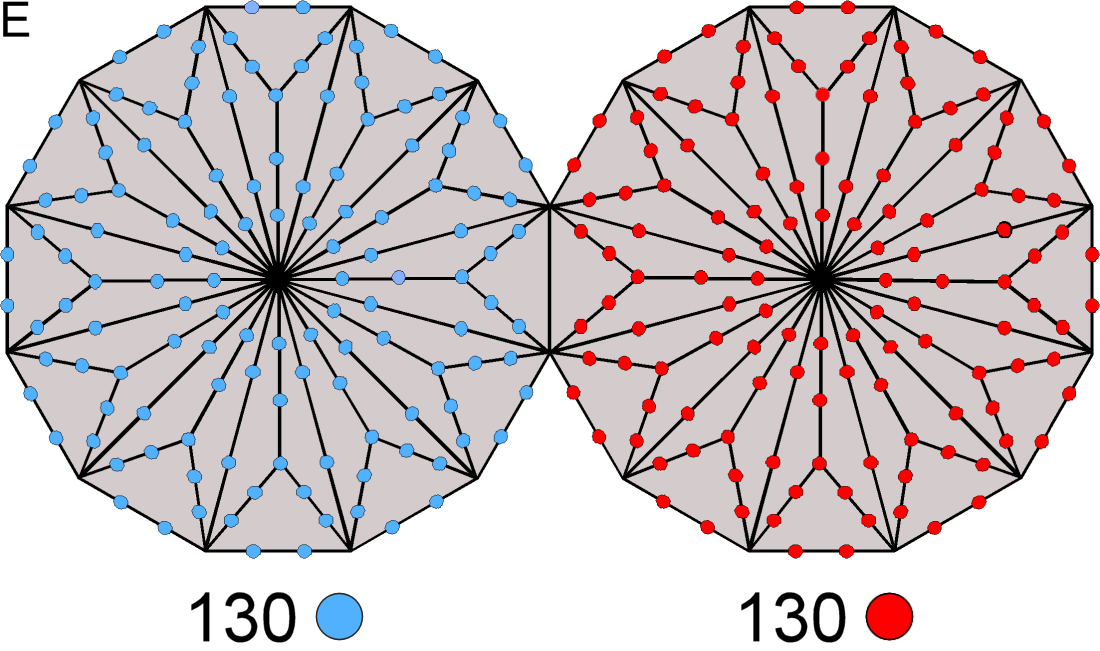
G. The number of yods in a Type B n-gon = 15n + 1. They comprise (2n+1) corners of 3n tetractyses and 13n hexagonal yods. A Type B decagon has 30 tetractyses with 21 corners and 130 hexagonal yods. Symbolising the perfection of number in the Decad, or number 10, according to the ancient Pythagoreans, the decagon contains 130 hexagonal yods that symbolise the 7 Sephiroth of Construction. As discussed in (F), each of the two halves of the 7 enfolded Type A polygons in the inner Tree of Life has 130 yods, i.e., the yods in 13 tetractyses. This 13:13 division reappears in both the Type B dodecagon (the tenth type of regular polygon) and the ten-sided Type B decagon. The Pythagorean Decad determines the division of Divine Unity into two polar-opposite halves of the inner Tree of Life with the total yod population of 26 tetractyses, where 26 is the number value of YAHWEH, the Godname that signifies and embodies the unlimited, creative potential of God. |
|||||
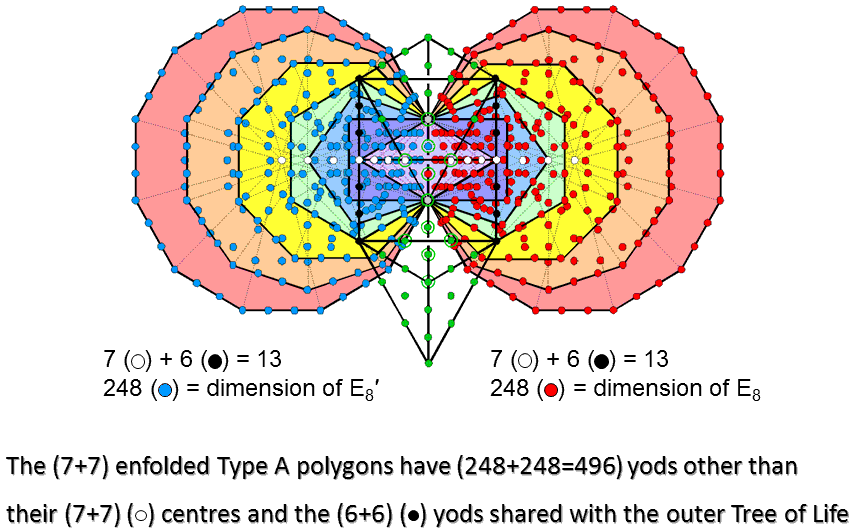
The 7 enfolded Type A polygons have 264 yods. Seven of them are their centres (coloured white). Above or below the centre of the hexagon are 3 black yods that lie on the right-hand pillar and are part of the outer Tree of Life when its 16 triangles are tetractyses. Therefore, (7+6=13) yods are either centres or shared with the outer Tree of Life. Similarly for the mirror-image set of 7 enfolded polygons on the other side of the root edge. (13+13=26) yods are either centres of the (7+7) enfolded polygons or shared with the outer Tree. The number 26 of YAHWEH determines the 498 yods surrounding the centres of the 14 polygons that are intrinsic to them. Two of them are the endpoints of the root edge, leaving 496 yods that are intrinsic to the polygons and surround their centres. 248 yods are associated with each half of the inner Tree of Life. This number is the dimension of E8. In confirmation of what has been shown in previous discussions, the symmetry group E8×E8 conforms to the inner form of the Tree of Life, its direct product character reflecting the fact that this inner form is composed of two halves, one of which is the mirror image of the other. The 13:13 division defines this equal distribution of the 496 intrinsic yods that surround centres of polygons.
The dimension 496 of E8×E8 is embodied in the combined outer & inner Trees of Life as their 496 hexagonal yods (see third diagram here).
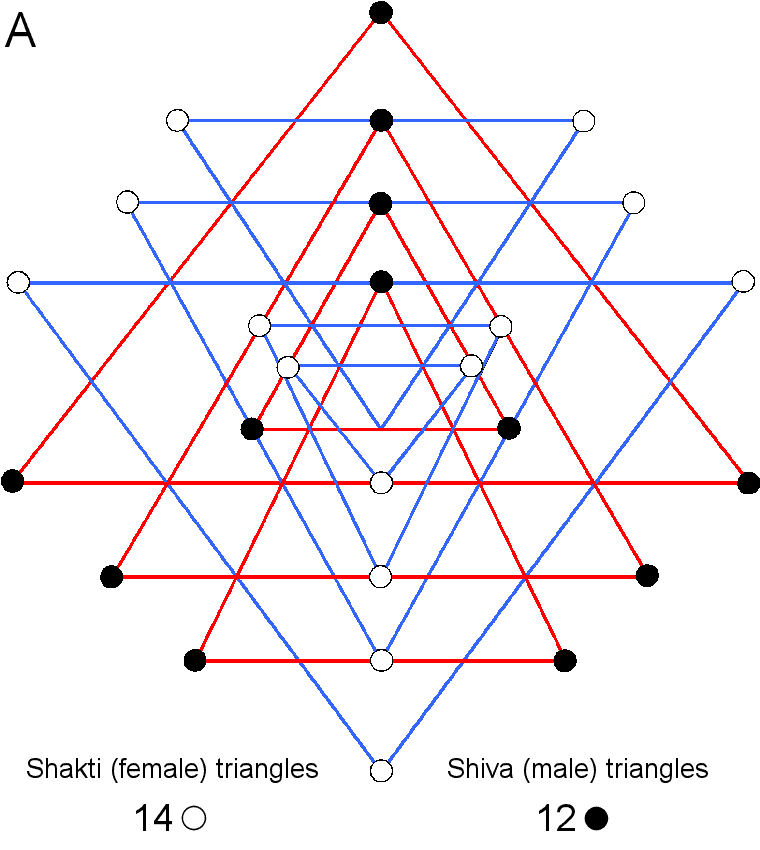
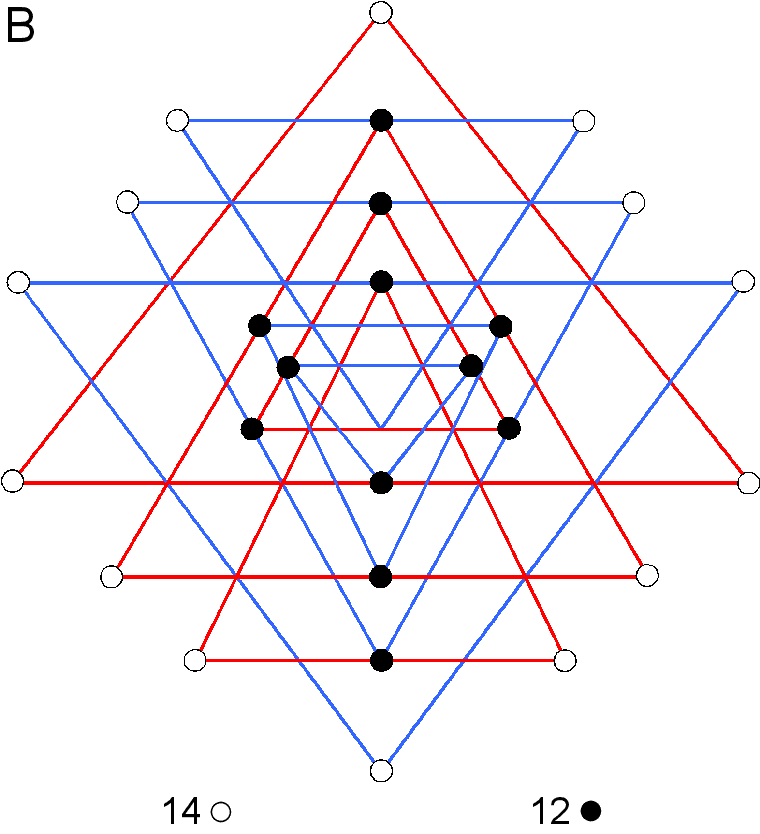
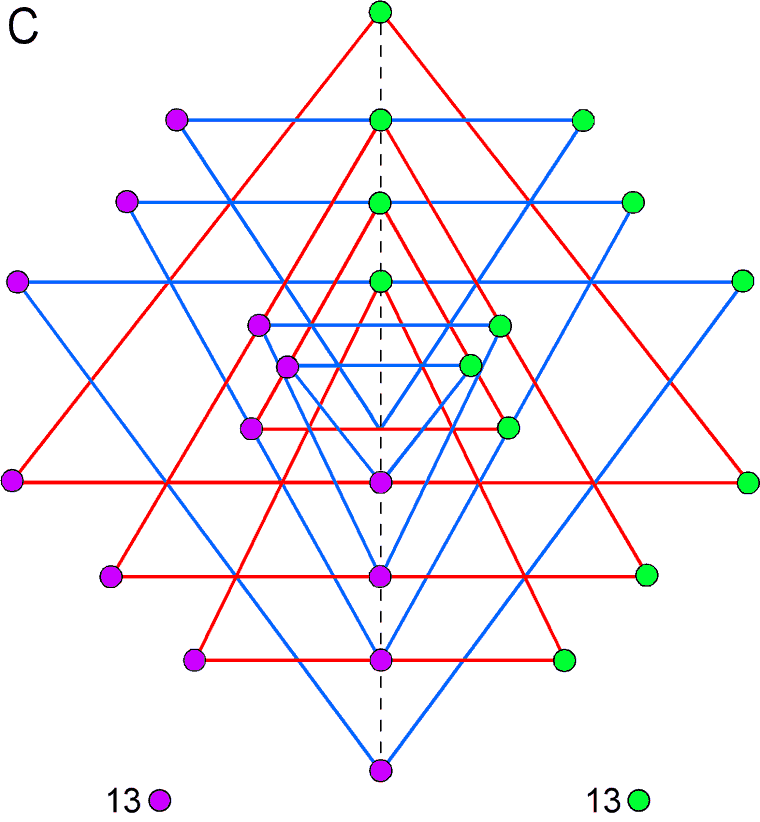
A. The 9 primary triangles that generate the Sri Yantra have 26 corners surrounding the downward-pointing triangle at its centre (their 27th corner is the lowest corner of this triangle). The 5 downward-pointing triangles expressing the Shakti (feminine) principle have 14 white corners surrounding the central triangle. The 4 upward-pointing triangles representing the Shiva (masculine) principle have 12 black corners. The 14 corners correspond to the 14 centres of the (7+7) enfolded polygons and the 12 corners correspond to the 12 shared yods on the two side pillars of the outer Tree of Life other than those at Chesed and Geburah, which coincide with the centres of the two hexagons.
B. The 3-d Sri Yantra comprises 4 layers of triangles. The lowest layer has 14 triangles whose 14 white tips correspond to the 14 centres of the (7+7) enfolded polygons. The 3 other layers have 28 triangles, of which 12 have the black corners of the 9 parent triangles. The (7+6) white/black corners in each half of the Sri Yantra correspond to the 7 centres & 6 shared yods in each half of the inner Tree of Life.
C. The Sri Yantra can be divided into two vertical halves, each containing 13 corners of the 9 parent triangles whose intersection generates the 43 triangles. Every violet yod has its mirror-image, reflected across the vertical mirror plane symbolised by the vertical, dashed line. The 8 tips of the 4 upward-pointing triangles and the 4 downward-pointing triangles lie on this line. The upper 4 green corners on this line can be associated with the right-hand set of corners and the lower 4 violet corners on the line can be associated with the left-hand set.
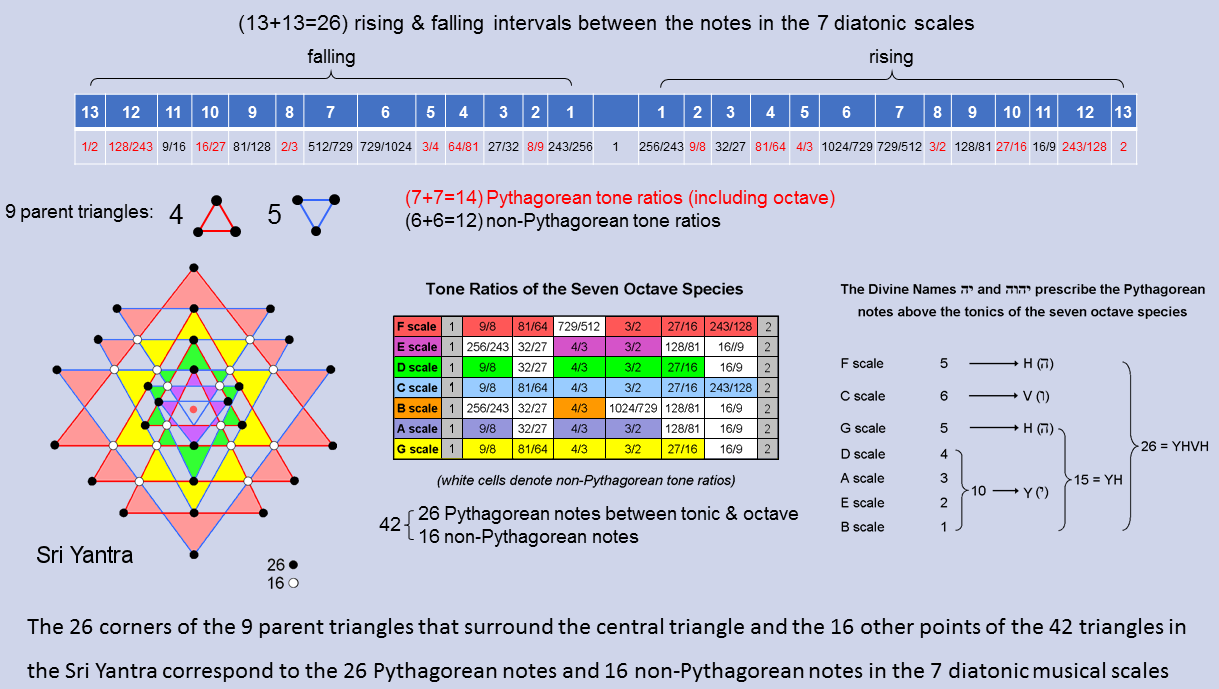
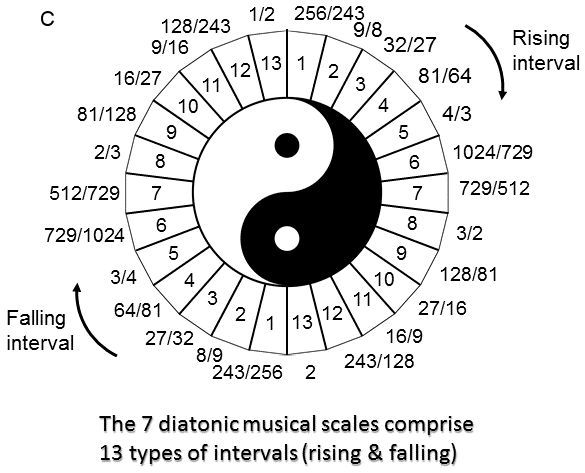
Including the octave, the 7 diatonic musical scales have 13 types of rising intervals.* They have 13 falling counterparts. Therefore, there are 26 types of rising & falling intervals between their notes. Formally counting the octave as a Pythagorean note because it belongs to the Pythagorean scale, there are (7+7=14) types of rising & falling, Pythagorean intervals (written in red in the diagram opposite) and (6+6=12) types of rising & falling, non-Pythagorean intervals (written in black).** As we have pointed out in the previous discussion, this 14:12 division in the number 26 appears in the Sri Yantra as the 14 corners of the 5 downward-pointing (Shakti) triangles that surround the centre triangle and the 12 corners of the 4 upward-pointing (Shiva) triangles. The 42 triangles surrounding the central triangle have 26 points provided by the 9 parent triangles, leaving 16 other points. This 26:12 division appears in the 7 diatonic scales as the 26 Pythagorean notes and 16 non-Pythagorean notes that make up the (7×6=42) notes between their tonics and octaves. The Divine Name YAHWEH prescribes both features because the Sri Yantra and the 7 diatonic scales are analogous, holistic systems, the points of the 42 triangles in the former denoting their 42 notes. The gematria number values of the 4 letters of this Divine Name are the numbers of Pythagorean notes in various scales. Two alternative schemes to that shown are possible:
1. D & E scales → 6 (=V) and A, B, & C scales → 10 (=Y);
2. A, B & E scales → 6 (=V) and C & D scales → 10 (=Y).
The depicted scheme seems the most natural because it has more letters with number values that denote numbers of Pythagorean notes in a single scale.
* The rising interval between two notes with tone ratios m & n (m>n) is m/n. Their falling interval is n/m. The tonic has tone ratio 1, so that a falling interval 1/n can be associated with every note with tone ratio n.
** A "falling Pythagorean interval" is not necessarily an actual note of the next lower octave of the Pythagorean scale. In fact, only the perfect fourth with tone ratio 4/3 and the perfect fifth with tone ratio 3/2 have this property. Proof: the tone ratios of a note (n) and its inversion (m) are related by nm = 2. Therefore, 1/n = ½×m. A note with tone ratio 1/n is, respectively, Pythagorean or non-Pythagorean only if m is Pythagorean or non-Pythagorean. The only Pythagorean notes having tone ratios whose reciprocals are tone ratios of notes in the next lower octave of the Pythagorean scale are found by inspection to be the perfect fourth and perfect fifth: 3/4 = ½×3/2 and 2/3 = ½×4/3. Therefore, a "falling Pythagorean interval" does not mean a falling interval that is a note of the next lower octave of the Pythagorean scale, It simply means the reciprocal of the tone ratio of a note belonging to this scale.