The two separate halves of the inner Tree of Life encode the 240 roots of E₈

The 240 roots of the rank-8, exceptional Lie group E₈ are represented by 240 vectors in 8-dimensional, Euclidean space. These vectors all have the same length (by convention, it is taken to be √2). These vectors are the position vectors of the 240 vertices of the semi-regular polytope called the "Gosset polytope," or 4₂₁ polytope (this is discussed here). The 240 roots comprise 112 roots whose vector coordinates are all integers and 128 roots whose coordinates are all half-integers, in both cases the sum of the coordinates for each root vector being even. The diagram above displays their explicit forms as 8-tuples. The 28 permutations of (−1, −1, 0, 0, 0, 0, 0, 0) are the mirror images of the 28 permutations of (1, 1, 0, 0, 0, 0, 0, 0). The 56 permutations of (1, −1, 0, 0, 0, 0, 0, 0) contain their mirror images, so that it contains 28 permutations and their 28 mirror images, in which +1 → −1 & −1 → +1. The 28 permutations of (−½, −½, −½, −½, −½, −½, ½, ½) are the mirror images of the 28 permutations of (−½, −½, ½, ½, ½, ½, ½, ½). There are 168 permutations that consist of three sets of 28 permutations (i.e., 84 permutations) and three sets of their mirror images (another 84 mirror images), so that they comprise six sets of 28 root vectors. The remaining 72 roots consist of 70 permutations of (−½, −½, −½, −½, ½, ½, ½, ½), that is, 35 permutations and their mirror images, and two roots, namely, (½, ½, ½, ½, ½, ½, ½, ½) and its mirror image (−½, −½, −½, −½, −½, −½, −½, −½). The 72 roots comprise (35+1=36) roots and their 36 mirror images.

When their 47 sectors are tetractyses, the seven enfolded polygons making up each half of the inner Tree of Life have 120 yods lining their boundaries. They comprise 36 corners and 84 hexagonal yods. The topmost corner of the hexagon coincides with the lowest corner of the hexagon enfolded in the next higher Tree of Life. It is the only corner of any of the seven polygons that is not intrinsic to them. It is coloured black in the diagram above, its counterpart in the mirror image set of polygons being coloured white. The 36 corners of each half of the inner Tree of Life consist of 35 intrinsic corners (coloured grey) and one corner shared with the inner form of the next higher Tree. Both separate halves contain 72 corners that comprise 70 intrinsic corners and two shared corners.

If the two hexagonal yods in the shared root edge are associated with the dodecagon, this polygon can be paired only with the triangle to create 14 sides with 28 hexagonal yods. This in turn means that the decagon can be combined only with the hexagon to create 14 sides, which means that the octagon can be combined only with the square and pentagon to create 14 sides with 28 hexagonal yods. If, instead. the two hexagonal yods are associated with another polygon (indicated below by two enclosing brackets), there are six possible combination schemes that can generate three sets of 28 hexagonal yods:

Such ambiguity in correspondence between hexagonal yods and roots of E₈ is unattractive because, unless there is a plausible reason why it should exist (and there is none here), a unique, one-to-one correspondence should exist between hexagonal yods and these roots. Associating the root edge with the dodecagon is the most likely possibility because it leads to a unique, triple combination of polygons with 28 hexagonal yods in their 14 sides.

Comparing the six sets of 28 permutations of the 8-tuples with the sets of yods lining sides of the polygons in the two halves of the inner Tree of Life, the 72 corners correspond to the 72 8-tuples of the last three types listed in the diagram and the 168 hexagonal yods correspond to the 168 8-tuples of the first five types. The two chiral halves of the inner Tree of Life with 120 boundary yods correspond to the 120 8-tuples and their 120 mirror images. The two shared corners of the hexagons correspond to the root at (½, ½, ½, ½, ½, ½, ½, ½,) and its mirror image at (−½, −½, −½, −½, −½, −½, −½, −½).

The maximal, single subgroup of E₈ is O₁₆, which has 120 roots. It has the subgroup O₈ with 28 roots.

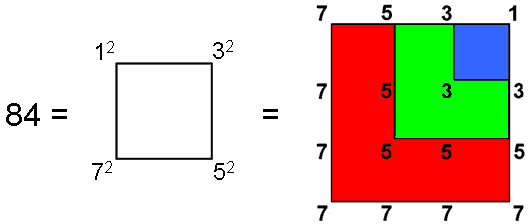
Eighty-four hexagonal yods line the 42 sides of the seven enfolded polygons making up each half of the inner Tree of Life, where

84 = 1² + 3² + 5² + 7².

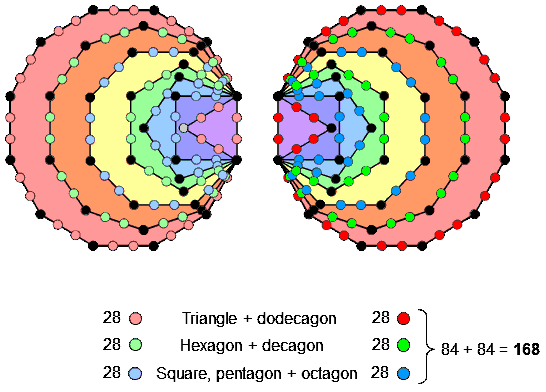
This illustrates the Tetrad Principle (see Article 1) at work, expressing characteristic parameters of holistic systems. The 2×84 and 3×56 factorizations displayed by the 168 hexagonal yods that line the 84 sides of the two sets of seven enfolded polygons have their counterparts in other sacred geometries, as well as in the geometry of the inner Tree of Life itself. For example, Article 64 shows that the triangle, square, pentagon & dodecagon have 84 intrinsic geometrical elements, as do the hexagon, octagon & decagon. The 56 hexagonal yods that line sides in each of the following three sets of polygons:

1. Triangle & dodecagon 
2. Hexagon & decagon 
3. Square, pentagon & octagon 

correspond in:

• the 64 hexagrams used in the I Ching system of divination to the 56 trigrams making up the 168 lines & broken lines in the 28 off-diagonal hexagrams on either side of the diagonal of the 8×8 array of hexagrams. The three rows of a trigram, each repeated 28 times, correspond to these three sets of polygons with 28 hexagonal yods in each set. The pairing of trigrams into a hexagram corresponds to the two separate halves of the inner Tree of Life, each with 84 hexagonal yods lining sides of the seven enfolded polygons. Each hexagonal yod on their boundaries corresponds to a line or broken line;
• the disdyakis triacontahedron, whose 120 faces have 180 edges, to the 28 AB edges, the 28 BC edges and the 28 AC edges that are above and below its equator formed by 12 edges. In other words, the three types of edges that this polyhedron has correspond to the three sets of polygons. Each hexagonal yod, repeated 28 times in each set of polygons, denotes one of three types of edges, each of which is repeated 28 times above and below the equator of the polyhedron;
• the 168 repetitions of rising and falling, Pythagorean intervals between the notes of the seven diatonic scales as the 56 repeated, rising and falling D intervals, the 56 repeated, rising and falling E & G intervals and the 56 repeated, rising & falling F & A intervals. In other words, there are just three sets of Pythagorean intervals between the notes in these scales that get repeated 28 times. Each hexagonal yod corresponds to a repetition of a Pythagorean note interval — those in one set of polygons denoting a rising interval and those in the set belonging to the mirror image half of the inner Tree of Life denoting a falling interval.

(for details of these and other correspondences, see here). They illustrate that the factorisation: 168 = 2×3×28 is characteristic of the geometrical and yod compositions of holistic systems. For example, as evidence that the dodecagon is the single, polygonal representation of the inner Tree of Life, 168 extra yods are needed to construct the Type B dodecagon from 36 tetractyses:

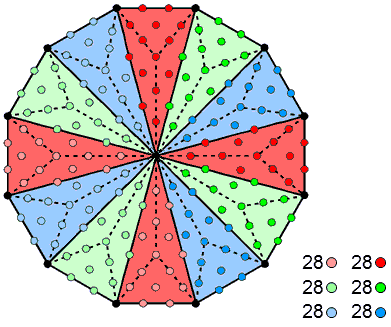
The 2×3×28 yods in the inner Tree of Life and the Type B dodecagon.

28 yods make up any sector and its mirror image on the opposite side. This is indicated in the diagram above as the 28 yods other than corners of the dodecagon that are coloured either dark red, dark green or dark blue and their 28 lighter coloured counterparts in the sectors opposite them. Each pair of sectors containing 28 yods of the same colour corresponds in the two halves of the inner Tree of Life to each of the six combinations of polygons with 28 hexagonal yods on their sides.

This 2×3×28 factorisation also appears in the two separate triangles making up the inner Tree of Life when they are Type C. The number of corners, sides & triangles that surround the centre of a Type C n-gon = 28n. Hence, a Type C triangle is composed of 85 points, lines & triangles, where

85 = 4⁰ + 4¹ + 4² + 4³.

84 geometrical elements surround surround its centre, where

84 = 1² + 3² + 5² + 7².

The centres of the two separate Type C triangles in the inner form of the Tree of Life are surrounded by (84+84=168) geometrical elements:

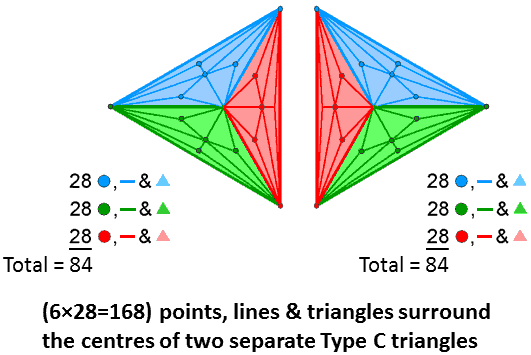
As there are 28 such geometrical per red, green & blue sector of a Type C triangle, the 168 elements comprise three pairs of sectors (one from each triangle) of each colour made up of (28+28=56) elements. Therefore, the pair of Type C triangles embodies the 2×3×28 factorisation of the holistic parameter 168 displayed by the complete inner Tree of Life, the Type B dodecagon and other sacred geometries. This is the number of roots of the exceptional Lie group E₈ that are not roots of its exceptional subgroup E₆. Notice that, as the 28 geometrical elements per sector consist of 14 corners & triangles and 14 sides, the two Type C triangles comprise (2×3×14=84) corners & triangles and (2×3×14=84) sides. Hence, the factor of 2 in the 2×3×28 factorisation of 168 may, alternatively, be understood as arising from the fact that the geometrical elements per sector of a polygon (whatever its number of corners) always divide into two subsets, one of which has the same number of points & triangles as the other has lines. This is true whether the polygon is Type A, B, C, etc.* For example, for a Type A polygon, there are two sides, one corner and one triangle (i.e., two corners & triangles), per sector; for a Type B polygon, there are five sides, two corners and three triangles (i.e., five corners & triangles) per sector.

* Proof: The number of corners per sector increases with type of polygon (Type A, Type B, Type C, Type D, etc) as 1, 2, 2 + 3¹, 2 + 3², etc, the number of sides increases as 2, 2 + 3¹, 2 + 3¹ + 3², 2 + 3¹ + 3², etc, and the number of triangles increases as 1, 3¹, 3², 3³, etc. The nth type of polygon (n = 1, 2, 3, etc) has C_n corners, S_n sides & T_n triangles, where:

C_n = 1 + 3⁰ + 3¹ +... + 3ⁿ⁻² = (1+3ⁿ⁻¹)/2,

S_n = 1 + 3⁰ + 3¹ + +... + 3ⁿ⁻¹ = (1+3ⁿ)/2,

and

T_n = 3ⁿ⁻¹.

Therefore,

 C_n + T_n = (1+3ⁿ⁻¹)/2 + 3ⁿ⁻¹ = (1+3ⁿ)/2 = S_n.

<< Previous    1...   39  40  [41]  42  43  ...50    Next >>

Home