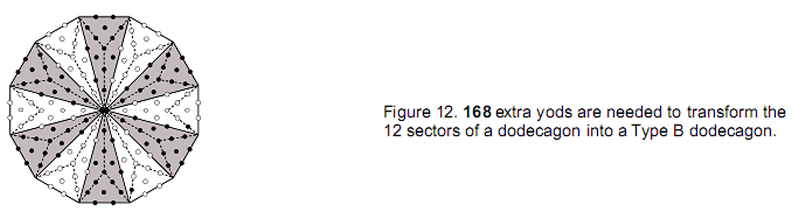ARTICLE 48

by
Stephen M. Phillips
Flat 4, Oakwood House, 117-119 West Hill Road. Bournemouth. Dorset BH2 5PH. England.
Website: http://www.smphillips.mysite.com
Abstract
|
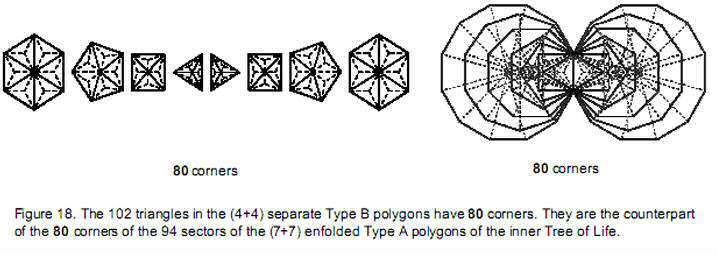
As a development of earlier work showing that certain subsets of the (7+7) polygons of the inner form of the Tree of Life have analogous properties to the latter, this article proves that the first (4+4) polygons also constitute such a subset. It analyses their geometrical composition and their yod populations generated from tetractyses of 10 points (“yods”) by regarding them as either Type A or Type B polygons. Through their gematria number values, the Godnames of the 10 Sephiroth of the Tree of Life prescribe the first (4+4) polygons. The Decad determines the 120 geometrical elements outside the shared, root edge of the (4+4) enfolded Type A polygons because 120 is the sum of the first 10 odd integers after 1. Previous articles have established that the number 90 is a parameter of holistic systems, e.g., the five Platonic solids have 90 edges and the sum of the integers in the Platonic Lambda Tetractys is 90. It appears in the first four separate Type B polygons as the 90 sides of their 54 triangles and as their 90 corners & triangles. The first four enfolded Type A polygons also have 90 yods outside their root edge. The 108 sectors of the (4+4) separate Type B polygons have 260 corners & sides. Their counterparts in the inner Tree of Life are the 260 yods in the seven enfolded Type A polygons outside their root edge. The first four separate Type B polygons embody the 248 roots of the superstring gauge symmetry group E8 as the 248 yods other than corners that are outside their root edges. Enfolded, these polygons have 247 yods. Their counterparts in the inner Tree of Life are the 247 yods lining sides of tetractys sectors of the seven separate Type A polygons. 192 yods outside the root edge line the sides of the tetractyses making up each set of the first four enfolded Type B polygons. This 192:192 division is characteristic of representations of holistic systems, being found, for example, in the 192 lines and 192 broken lines that make up the 64 hexagrams in the I Ching table. The (248+248) yods outside the root edge of two joined, Type C hexagons symbolise the (248+248) roots of the heterotic superstring gauge symmetry group E8×E8'. With 2nd-order tetractyses as sectors, two joined hexagons have 840 yods outside the root edge. This is the number of circular turns in the inner or outer halves of each helical whorl of the basic unit of matter described by the Theosophists Annie Besant and C.W. Leadbeater. The 10 pairs of Type A hexagons enfolded in 10 overlapping Trees of Life have (840+840) yods that symbolise the (840+840) turns in a whorl. The 80 corners of the 108 triangles in the first (4+4) separate Type B polygons correspond to the 80 corners of the 94 sectors of the (7+7) enfolded Type A polygons of the inner Tree of Life. They also correspond to the 80 yods in the lowest Tree of Life. These and other correspondences demonstrate that the first (4+4) polygons constitute a holistic structure that is isomorphic to the greater whole of the inner Tree of Life. |
1
Table 1. Gematria number values of the 10 Sephiroth in the four Worlds.
|
SEPHIRAH |
GODNAME |
ARCHANGEL |
ORDER OF ANGELS |
MUNDANE CHAKRA |
|
| 1 | Kether (Crown) 620 |
EHYEH (I am) 21 |
Metatron (Angel of the Presence) 314 |
Chaioth ha Qadesh (Holy Living Creatures) 833 |
Rashith ha Gilgalim First Swirlings. (Primum Mobile) 636 |
| 2 | Chokmah (Wisdom) 73 |
YAHWEH, YAH (The Lord) 26, 15 |
Raziel (Herald of the Deity) 248 |
Auphanim (Wheels) 187 |
Masloth (The Sphere of the Zodiac) 140 |
| 3 | Binah (Understanding) 67 |
ELOHIM (God in multiplicity) 50 |
Tzaphkiel (Contemplation of God) 311 |
Aralim (Thrones) 282 |
Shabathai Rest. (Saturn) 317 |
| Daath (Knowledge) 474 |
|||||
| 4 | Chesed (Mercy) 72 |
EL (God) 31 |
Tzadkiel (Benevolence of God) 62 |
Chasmalim (Shining Ones) 428 |
Tzadekh Righteousness. (Jupiter) 194 |
| 5 | Geburah (Severity) 216 |
ELOHA (The Almighty) 36 |
Samael (Severity of God) 131 |
Seraphim (Fiery Serpents) 630 |
Madim Vehement Strength. (Mars) 95 |
| 6 | Tiphareth (Beauty) 1081 |
YAHWEH ELOHIM (God the Creator) 76 |
Michael (Like unto God) 101 |
Malachim (Kings) 140 |
Shemesh The Solar Light. (Sun) 640 |
| 7 | Netzach (Victory) 148 |
YAHWEH SABAOTH (Lord of Hosts) 129 |
Haniel (Grace of God) 97 |
Tarshishim or Elohim 1260 |
Nogah Glittering Splendour. (Venus) 64 |
| 8 | Hod (Glory) 15 |
ELOHIM SABAOTH (God of Hosts) 153 |
Raphael (Divine Physician) 311 |
Beni Elohim (Sons of God) 112 |
Kokab The Stellar Light. (Mercury) 48 |
| 9 | Yesod (Foundation) 80 |
SHADDAI EL CHAI (Almighty Living God) 49, 363 |
Gabriel (Strong Man of God) 246 |
Cherubim (The Strong) 272 |
Levanah The Lunar Flame. (Moon) 87 |
| 10 | Malkuth (Kingdom) 496 |
ADONAI MELEKH (The Lord and King) 65, 155 |
Sandalphon (Manifest Messiah) 280 |
Ashim (Souls of Fire) 351 |
Cholem Yesodoth The Breaker of the Foundations. The Elements. (Earth) 168 |
|
The Sephiroth exist in the four Worlds of Atziluth, Beriah, Yetzirah and Assiyah. Corresponding to them are the Godnames, Archangels, Order of Angels and Mundane Chakras (their physical manifestation, traditionally symbolised by celestial bodies). This table gives their number values obtained by the ancient practice of gematria, wherein a number is assigned to each letter of the alphabet, thereby giving to a word a number value that is the sum of the numbers of its letters. |
(All numbers in this table referred to in the article are written in boldface).
2
1. Geometrical properties of the first four polygons
Many previous articles have established the role of the
Tetrad Principle in determining the properties of holistic systems embodying the 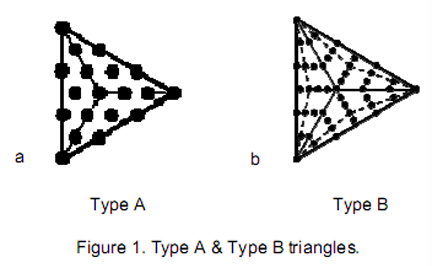 universal design or pattern found in the sacred geometries of some major
religions, as well as in objects well-known to mathematicians. They have revealed numerous
examples of how the Tetrad (4) and the integers 1, 2, 3 & 4 symbolized by the four rows of dots in
Pythagoras’ tetractys define or express the attributes of these systems. In view of this, the
first four regular polygons of the inner Tree of Life and the hexagon — the fourth polygon —
might therefore be expected to display defining parameters of these systems, such as the numbers
384, 248 & 168. This expectation will be confirmed by examining their
geometrical and yod composition. The appearance of so many of the 50 gematria number values
(shown in boldface) of the ancient Hebrew names of the 10 Sephiroth of the Tree of Life and
their manifestation in the four Kabbalistic Worlds of Atziluth, Beriah, Yetzirah & Assiyah
(Table 1) cannot, plausible, be explained away in terms of coincidence because
their occurrence is too frequent to be due to chance. Instead, these numbers are signatures of
the underlying sacred geometrical nature of these polygons. Previous articles have shown that
various subsets of the (7+7) regular polygons making up the inner Tree of Life are counterparts
of the whole set in the sense that their properties are analogous, being measured by the same
set of parameters. The first (4+4) regular polygons are another example of this amazing
fractal-like property of the inner Tree of Life, wherein smaller and smaller subsets of the 14
polygons display analogous properties quantified by the same set of numbers, namely,
the number values of the 10 Sephiroth, their Godnames, Archangels, Orders of Angels &
Mundane Chakras.
universal design or pattern found in the sacred geometries of some major
religions, as well as in objects well-known to mathematicians. They have revealed numerous
examples of how the Tetrad (4) and the integers 1, 2, 3 & 4 symbolized by the four rows of dots in
Pythagoras’ tetractys define or express the attributes of these systems. In view of this, the
first four regular polygons of the inner Tree of Life and the hexagon — the fourth polygon —
might therefore be expected to display defining parameters of these systems, such as the numbers
384, 248 & 168. This expectation will be confirmed by examining their
geometrical and yod composition. The appearance of so many of the 50 gematria number values
(shown in boldface) of the ancient Hebrew names of the 10 Sephiroth of the Tree of Life and
their manifestation in the four Kabbalistic Worlds of Atziluth, Beriah, Yetzirah & Assiyah
(Table 1) cannot, plausible, be explained away in terms of coincidence because
their occurrence is too frequent to be due to chance. Instead, these numbers are signatures of
the underlying sacred geometrical nature of these polygons. Previous articles have shown that
various subsets of the (7+7) regular polygons making up the inner Tree of Life are counterparts
of the whole set in the sense that their properties are analogous, being measured by the same
set of parameters. The first (4+4) regular polygons are another example of this amazing
fractal-like property of the inner Tree of Life, wherein smaller and smaller subsets of the 14
polygons display analogous properties quantified by the same set of numbers, namely,
the number values of the 10 Sephiroth, their Godnames, Archangels, Orders of Angels &
Mundane Chakras.
A polygon with n sides is known in mathematics as an ‘n-gon.’ It is transformed into a Type A polygon by dividing it up into its n sectors, which may then be further turned into tetractyses. Figure 1a shows the Type A triangle, or 3-gon with its three sectors turned into tetractyses. When each sector of the n-gon is divided into three sectors and each new sector turned into a tetractys, it becomes a Type B n-gon (Fig. 1b shows the Type B triangle). This transformation may be extended indefinitely, creating Type C n-gons, Type D n-gons, etc. This article will consider only Type A, Type B & Type C n-gons.
Instead of dividing sectors into ever smaller triangles/tetractyses, they may be regarded as members of an infinite sequence of nth-order tetractyses as ever greater differentiations of Unity (the Monad):
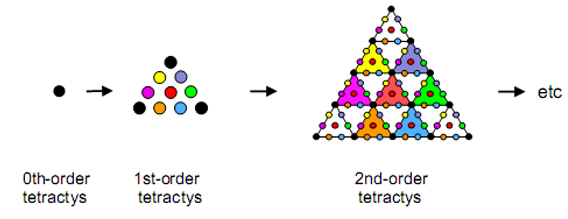
We shall consider only the 1st- and 2nd-order tetractyses. In this section, we shall examine the geometrical properties of the triangle, square, pentagon & hexagon, considering, firstly, the case when they are Type A polygons and then when they are Type B. The next section will analyse their construction from tetractyses in each case.
The following formulae are useful for examining geometrical properties of n-gons:
|
Type A n-gon |
Type B n-gon
|
|
|
Number of corners = |
n+1
2n n 3n+1 2n+1 3n 4n+1 |
2n+1
5n 3n 7n+1 5n+1 8n 10n+1 |
3
First four Type A polygons
The separate polygons will be considered first.
First four separate
polygons
Table 2 shows the geometrical composition of each Type A polygon:
Table 2. The geometrical composition of the first four separate Type A polygons.
| triangle | square | pentagon | hexagon | Total | |
|
Number of corners of sectors = |
3+1 | 4+1 | 5+1 | 6+1 | 18+4 |
|
Number of sides = |
6 | 8 | 10 | 12 | 36 |
|
Number of triangles = |
3 | 4 | 5 | 6 | 18 |
|
Number of corners & sides = |
9+1 | 12+1 | 15+1 | 18+1 | 54+4 |
|
Number of corners & triangles = |
6+1 | 8+1 | 10+1 | 12+1 | 36+4 |
|
Number of sides & triangles = |
9 | 12 | 15 | 18 | 54 |
| Number of corners, sides & triangles = | 12+1 | 16+1 | 20+1 | 24+1 | 72+4 |
First (4+4) separate polygons
- Number of corners of polygons = 2×18 = 36.
- Number of sides of polygons = 2×18 = 36.
- Number of corners & sides of polygons = 2×36 = 72.
- Number of triangles = 2×18 = 36.
- Number of corners of triangles = 2×22 = 44.
- Number of sides of triangles = 2×36 = 72.
- Number of corners & sides of triangles = 2×58 = 116.
- Numbers of corners & triangles = 2×40 = 80.
- Number of sides & triangles = 2×54 = 108.
- Number of corners, sides & triangles = 2×76 = 152. There are (152 – 4×3 = 140) geometrical elements outside the sides that become the root edge when the polygons are enfolded.
Comments
-
72 corners, sides & triangles surround the centres of the four polygons. They have 76 geometrical elements. The two sets of polygons separated by the root edge have 2×76 + 3 = 155 geometrical elements. ADONAI MELEKH, the Godname of Malkuth with number value 155 and YAHWEH ELOHIM, the Godname of Tiphareth with number value 76, prescribe the geometrical composition of the polygons. 140 elements are outside the root edges of the (4+4) polygons, where 140 is the number value of Malachim, the Order of Angels assigned to Tiphareth. ELOHA, the Godname of Geburah with number value 36, prescribes the number of sides of triangles in each set of four polygons, as well as the number of triangles in both sets. It also prescribes the total number of geometrical elements surrounding the centres of each set because 72 is the 36th even integer.
-
(2×72=144) geometrical elements surround the centres of the
(4+4) polygons, where
144 =
10 20 30 40
11 21 31 41
12 22 32 42
13 23 33 43
- The (4+4) polygons have 80 corners & triangles, where 80 is the number value of Yesod.
First four enfolded polygons
-
Number of corners of polygons = 3 + (4–2=2) + (5–2=3) + (6–2=4) = 12; (12–2=10) corners are outside their root edges (“external”).
- Number of sides of polygons = 3 + (4–1=3) + (5–1=4) + (6–1=5) = 15; (15–1=14) sides are external.
- Number of corners & sides of polygons = 12 + 15 = 27; (27–3=24) corners & sides are external.
- Number of triangles = 18 – 1 = 17 (the triangle fills one sector of the hexagon).
4
- Number of corners of triangles = (3+1=4) + (2+1=3) + (3+1=4) + 4 = 15; (15–2=13) are external.
- Number of sides of triangles = (3+3=6) + (3+4=7) + (4+5=9) + (5+4=9) = 31; (31–1=30) are external.
- Number of corners & sides of triangles = 15 + 31 = 46; (46–3=43) are external.
- Number of triangles & their sides = 17 + 31 = 48.
- Number of corners, sides & triangles = 46 + 17 = 63; (63–3=60) are external.
First (4+4) enfolded polygons
- Number of corners of polygons = 2×10 + 2 = 22; (22–2=20) are external.
- Number of sides of polygons = 2×14 + 1 = 29; (29–1=28) are external.
- Number of corners & sides of polygons = 22 + 29 = 51; (51–3=48) are external.
- Number of corners of triangles = 2×13 + 2 = 28; (28–2=26) are external.
- Number of sides of triangles = 2×30 + 1 = 61; (61–1=60) are external.
- Number of triangles = 2×17 = 34.
- Number of corners & sides of triangles = 28 + 61 = 89; (89–3=86) are external.
- Number of corners & triangles = 28 + 34 = 62; (62–2=60) are external.
- Number of triangles & their sides = 34 + 61 = 95.
- Number of corners, sides & triangles = 89 + 34 = 123; (123–3=120) are external.
Comments
-
The first four enfolded polygons have 15 sides and 15 corners of 17 sectors with 31 sides, showing how YAH, the Godname of Chokmah with number value 15, and EL, the Godname of Chesed with number value 31, prescribes the shape of the four polygons. They have 63 geometrical elements. The top corner of the hexagon coincides with the bottom corner of the hexagon enfolded in the next higher, overlapping Tree of Life. This means that 62 elements are intrinsic to each set of the first four enfolded polygons. The number 62 is the 31st even integer and the number value of Tzadkiel, the Archangel of Chesed. The first (4+4) enfolded polygons also have 62 corners & sectors. YAHWEH with number value 26 prescribes the 26 corners of sectors outside the root edge.
-
120 geometrical elements are outside the root edge of the first (4+4) enfolded polygons, where
120 = 22 + 42 + 62 + 82.
Two of the 123 geometrical elements (top corners of the two hexagons) in the first (4+4) enfolded polygons are shared with the corresponding polygons enfolded in the next higher Tree of Life. The number of intrinsic geometrical elements = 123 – 2 = 121 = 112. i.e., it is the square of the tenth integer after 1, 120 is the sum of the first 10 odd integers after 1, showing how the Decad determines the geometrical composition of the first (4+4) polygons. 30 sides of sectors and 30 corners & sectors lie on either side of the root edge, where
-
The 34 sectors of the first (4+4) enfolded polygons have 89 corners & sides. As the top corners of both hexagons coincide with the bottom corners of the hexagons enfolded in the next higher Tree of Life, there are 87 corners & sides that are intrinsic to the first (4+4) enfolded polygons. 87 is the number value of Levanah, the Mundane Chakra of Yesod.
-
The first (4+4) enfolded polygons have 95 sectors & sides, where 95 is the number value of Madim, the Mundane Chakra of Geburah.
-
Outside the root edge are 48 corners & sides of the first (4+4) enfolded polygons. 48 is the number value of Kokab, the Mundane Chakra of Hod, and the number of triangles & sides in the four enfolded polygons. The first (4+4) enfolded polygons have 51 corners & sides. 51 is the 50th integer after 1. They have 49 intrinsic corners & sides. 49 is the number value of EL ChAI, the Godname of Yesod.
First four Type B polygons
We will next consider the first four Type B polygons, starting with the separate polygons.
First four separate polygons
Table 3 displays the properties of each separate Type B polygon:
Table 3. Geometrical composition of the first four, separate Type B polygons.
| triangle | square | pentagon | hexagon | Total | |
| Number of corners of sectors = |
6+1
|
8+1
|
10+1
|
12+1
|
36+4
|
|
Number of sides of sectors = |
15 |
20 | 25 | 30 | 90 |
|
Number of sectors = |
9 |
12 | 15 | 18 | 54 |
| Number of corners & sides of sectors = |
21+1 |
28+1 | 35+1 | 42+1 | 126+4 |
| Number of corners & sectors = |
15+1 |
20+1 | 25+1 | 30+1 | 90+4 |
| Number of sides & sectors = |
24 |
32 | 40 | 48 | 144 |
| Number of corners, sides & sectors = |
30+1 |
40+1
|
50+1 | 60+1 | 180+4 |
-
The first four polygons have 40 corners, where 40 = 4 + 8 + 12 + 16. Both sets of polygons have 80 corners, where 80 is the number value of Yesod. 36 corners surround the centres of each set of polygons. 72 corners surround the centres of both sets.
-
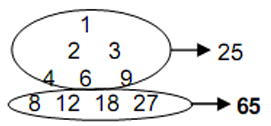
The first four polygons have 90 sides. 25 sides belong to the pentagon and 65 belong to the other three polygons. This 25:65 division has its counterpart in the Lambda Tetractys because the sum of its uppermost six integers is 25 and the sum of the four integers in its base is 65:
The 90 corners & triangles surround their centres comprise 36 corners and 54 triangles. Many previous articles have illustrated how this 36:54 division is characteristic of holistic systems, the sum of the integers at the corners of the Lambda Tetractys being 36 and the sum of the seven remaining integers being 54. This conformity to the archetypal Lambda Tetractys is a clear indication of the holistic nature of the first four polygons. The counterparts of this division in the five Platonic solids are the 36 sides of the tetrahedron and dodecahedron and the 54 sides of the octahedron, cube & icosahedron.
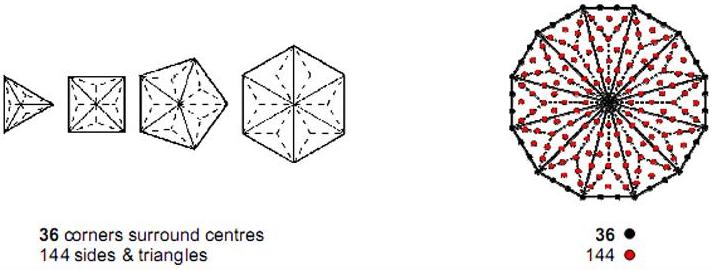
Figure 2. The 180 yods surrounding the centre of the Type B dodecagon symbolise
the 180 geometrical elements that surround the centres of the first four polygons.
- The first four polygons have 144 sides & triangles, where
|
144 = |
10 20 30
40 |
The first (4+4) polygons have 288 sides & triangles, where
288 = 11 + 22 + 33 + 44.
36 corners surround the centres of each set of four polygons, where 36 = (1+3+5+7) + (2+4+6+8), i.e., this number is the sum of the first four odd integers and the first four even integers. 360 geometrical elements surround the centres of both sets. This is the sum of the Decad (10) assigned to each of the 36 yods that surround the centre of the Type A hexagon (fourth polygon). These properties demonstrate how the Tetrad and the integers 1, 2, 3 & 4 symbolised by the tetractys express properties of this set of polygons.
-
180 corners, sides & triangles surround the centres of the first four polygons. They comprise 36 corners and 144 sides & triangles. The counterpart of this in the Type B dodecagon is the 180 yods that surround its centre. They comprise 36 yods that line its boundary and 144 yods in its interior (Fig. 2). Alternatively, there are 36 corners & sides shaping the polygons and 144 interior, geometrical elements. They are symbolised by the corresponding 36 yods on the boundary of the dodecagon and by the 144 yods inside it.
6
-
The 54 sectors of the first four polygons have 130 corners & sides, where 130 is the 65th even integer and the 129th integer after 1. The (4+4) polygons have 260 (=26×10) corners & sides. The seven enfolded polygons with their 47 sectors turned into tetractyses have 260 yods outside their root edge (Fig. 3a), whilst 260 yods other than the corners and centres of two joined, Type B dodecagons line the sides of their 72 tetractyses outside their shared edge (Fig. 3b).
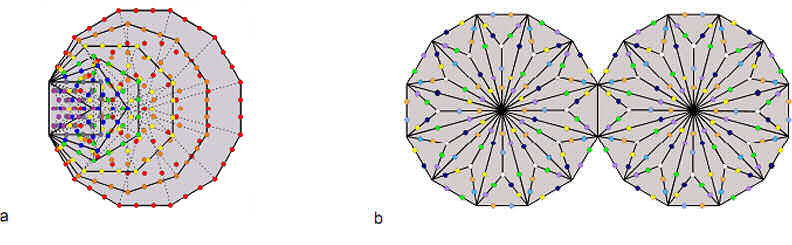
Figure 3. The Godname YAHWEH with number value 26 prescribes the 260 yods outside the root edge of the seven enfolded Type A polygons of
the inner Tree of Life and the 260 yods other than corners & centres of the Type B dodecagons that are outside the root edge on sides of tetractyses.
It is evidence that the first (4+4) polygons constitute a holistic system having properties analogous to those of the inner Tree of Life.
First four enfolded polygons
One of the sectors of the hexagon is replaced by the three sectors of the triangle when they become enfolded in one another. Table 4 displays the properties of the first four enfolded polygons:
Table 4. Geometrical composition of the first four enfolded Type B polygons.
| 4 enfolded polygons | (4+4) enfolded polygons | |
|
Number of corners of sectors = |
40 – 3×2 – 2 = 32 |
2×30 + 2 = 62 |
|
Number of sides of sectors = |
90 – 3 – 5 = 82 |
2×81 + 1 = 163 |
|
Number of sectors = |
54 – 3 = 51 |
2×51 = 102 |
|
Number of corners & sides of sectors = |
32 + 82 = 114 |
62 + 163 = 225 |
|
Number of corners & sectors = |
32 + 51 = 83 |
62 + 102 = 164 |
|
Number of sides & sectors = |
82 + 51 = 133 |
163 + 102 = 265 |
| Number of corners, sides & triangles = |
32 + 82 + 51 = 165 |
62 + 163 + 102 = 327 |
-
The four polygons have 32 corners, where 32 is the 31st integer after 1. The (4+4) polygons have 62 corners, where 62 is the number value of Tzadkiel, the Archangel of Chesed, which is the fourth Sephirah from the top of the Tree of Life. 31 corners are associated with each set, where 31 is the number value of EL, the Godname of Chesed. One is an endpoint of the root edge and there are 30 corners outside it. This reflects the number values E = 1 and L = 30.
-
The four polygons have 51 sectors, where 51 is the 50th integer after 1. The 114 corners & sides of their sectors comprise 12 corners and 15 sides of polygons, leaving 87 corners and sides generated by their transformation, where 87 is the number value of Levanah, the Mundane Chakra of Yesod.
-
The (4+4) polygons have 265 sides & triangles, that is, 264 sides & triangles are outside the root edge. This is the number of yods in the seven enfolded, Type A polygons (see Fig. 3).
-
There are 165 corners, sides & triangles in the four polygons, where
165 = 12 + 32 + 52 + 72 + 92.
Such a beautiful property is no accident but, instead, the manifestation of perfect mathematical design. They include the 12 polygonal corners, leaving 153 geometrical elements, where 153 is the number value of ELOHIM SABAOTH, the Godname of Hod. The (4+4) polygons have 327 geometrical elements. They include the three corners and two sides on each side pillar of the outer Tree of Life. This means that (327–5–5=317) geometrical elements are unshared with it. 317 is the number value of Shabathai, the Mundane Chakra of Binah.
2. Yod composition of the first four polygons
The following formulae are useful for studying the yod composition of n-gons:
7
|
Type A |
Type B |
|
| Number of yods at corners of tetractyses = |
n + 1 |
2n + 1 |
| Number of hexagonal yods = |
5n |
13n |
| Number of yods = |
6n + 1 |
15n + 1 |
First four Type A polygons
The first four separate polygons are considered first.
First four separate polygons
Table 5 shows the numbers of yods in the first four Type A polygons:
Table 5. Yod composition of the first four separate Type A polygons.
|
triangle |
square | pentagon | hexagon | Total | |
|
Number of corners of tetractyses = |
3+1 |
4+1 |
5+1 |
6+1 |
18+4 |
|
Number of hexagonal yods = |
15 |
20 |
25 |
30 |
90 |
|
Number of yods = |
18+1 |
24+1 |
30+1 |
36+1 |
108+4 |
| Number of yods outside root edge = |
14+1 |
20+1 |
26+1 |
32+1 |
92+4 |
-
Number of yods at corners of 18 tetractyses = 22.
-
Number of hexagonal yods = 15 + 20 + 25 + 30 = 90.
-
Number of yods = 19 + 25 + 31 + 37 = 112; 108 yods surround their centres.
-
Number of yods on boundaries of polygons = 18 + 2×18 = 54; (2×18=36) are hexagonal.
-
Number of yods on boundaries of tetractyses = 54 + 2×18 + 4 = 94; (94–22=72) are hexagonal.
First (4+4) separate polygons
-
Number of yods at corners of tetractyses = 2×22 = 44.
-
Number of hexagonal yods = 2×90 = 180.
-
Number of yods = 2×112 = 224. (2×108=216) yods surround their centres.
-
Number of yods on boundaries of polygons = 2×54 = 108; (2×36=72) are hexagonal.
- Number of yods on boundaries of tetractyses = 2×94 = 188; (2×72=144) are hexagonal.
First four enfolded polygons
-
Number of yods at corners of 17 tetractyses = 22 – 3×2 – 1 = 15 (13 outside root edge).
- Number of hexagonal yods = 90 – 3×2 – 2 – 2 – 1 = 79 (77 outside
root edge).
- Number of yods = 15 + 79 = 94 (90 outside root edge).
First (4+4) enfolded polygons
-
Number of yods at corners of 34 tetractyses = 2 + 2×13 = 28.
-
Number of hexagonal yods = 2 + 2×77 = 156; (156–2=154) are external.
-
Number of yods = 28 + 156 = 184; (184–4=180) are external.
-
Number of yods on 29 sides of polygons with 22 corners = 2×29 + 22 = 80; (80–4=76) are external.
-
Number of yods on sides of 34 tetractyses = 184 – 34 = 150 = 15×10; (150–4=146) are external, 73 on each side. Number of yods on sides of tetractyses other than 20 corners of polygons outside root edge = 150 – 20 = 130.
First four Type B polygons
The separate polygons are considered first.
First four separate polygons
Table 6 shows the numbers of yods in the four separate polygons:
Table 6. Yod composition of the first four separate Type B polygons.
|
triangle |
square | pentagon | hexagon | Total | |
|
Number of corners of tetractyses = |
6+1 |
8+1 |
10+1 |
12+1 |
36+4 |
|
Number of hexagonal yods = |
39 |
52 |
65 |
78 |
234 |
|
Number of yods = |
45+1 |
60+1 |
75+1 |
90+1 |
270+4 |
| Number of yods outside root edge = |
41+1 |
56+1 |
71+1 |
86+1 |
254+4 |
Comments
-
The first four polygons have 274 yods (18 corners and 256 other yods, where 256 = 44). This is a remarkable example of how the Tetrad expresses properties of holistic systems like these four polygons.
- There are 258 yods outside their sides that become the root edge when they are enfolded in one
8
another. The hexagon (fourth polygon) has 87 such yods, where 87 is the number value of Levanah, the Mundane Chakra of Yesod. Number of yods in the polygons outside their ‘root edges’ other than their 10 corners = 258 – 10 = 248. This is the number value of Raziel, the Archangel of Binah. It is the dimension of the superstring gauge symmetry group E8, the rank-8 exceptional Lie group. The polygons contribute to this number as follows:
|
triangle
|
square
|
pentagon
|
hexagon
|
|
| 248 = | 41 | 55 | 69 | 83 |
| = 22 non-polygonal corners + 226 hexagonal yods. |
||||
There are 54 hexagonal yods at centres of tetractyses, so that there are (54+22=76) yods that are either centres of tetractyses or their non-polygonal corners outside their root edges. This is how the Godname YAHWEH ELOHIM with number value 76 prescribes the embodiment of the 248 roots of E8 in the four separate Type B polygons. As the hexagon has 78 hexagonal yods, it has 76 hexagonal yods outside its root edge.
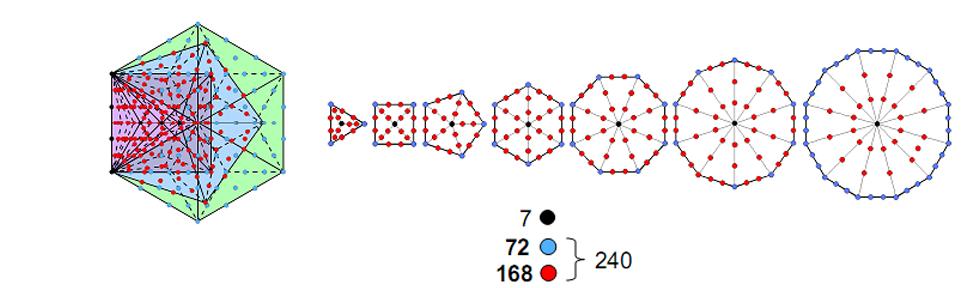
Figure 4. The first four enfolded Type B polygons have 240 yods outside the root edge surrounding their four centres. This is the number of yods on sides of tetractyses that surround the centres of the seven polygons of the inner Tree of Life. The 72 yods in the hexagon correspond to the 72 yods that either lie on the sides of the dodecagon or are corners of the first six polygons. The 168 yods outside the root edge surrounding the centres of the first three enfolded polygons correspond to the 168 yods surrounding the centres of the seven polygons that are either inside the dodecagon or are not corners of the first six polygons.
First four enfolded polygons
There are 19 yods (15 outside root edge) in the sector of the hexagon which coincides with the triangle. Four corners of tetractyses in the hexagon disappear when the polygons become enfolded. Table 7 shows the numbers of yods in the four enfolded polygons.
Table 7. Yod composition of the first four enfolded Type B polygons.
|
triangle |
square |
pentagon | hexagon | Total | |
|
Number of corners of tetractyses = |
7 |
9–2=7 |
11–2=9 |
13–4=9 |
32 |
|
Number of hexagonal yods = |
39 |
52–2=50 |
65–2=63 |
78–2–13=63 |
215 |
|
Number of yods = |
46 |
57 |
72 |
72 |
247 |
| Number of yods outside root edge = |
46–4–1=41 |
57–1=56 |
72–1=71 |
72 |
240 |
Comments
-
The first four enfolded polygons have 247 yods. This is the number of yods on the sides of the 48 sectors of the 7 separate polygons of the inner Tree of Life when the sectors are tetractyses (Fig. 4). 240 yods outside the root edge surround the centres of the polygons. 168 such yods are in the first

9
three and 72 yods are in the fourth. As illustrated in many previous articles, this 72:168 division is characteristic of holistic systems. It signifies the distinction between the 72 roots of E6, an exceptional subgroup of E8, and the remaining 168 roots of E8. It manifests in the E8×E8 heterotic superstring itself (Fig. 5) as the distinction between its three major whorls and its seven minor whorls, each of which carries 24 gauge charges of E8, according to the author’s work. There are also 240 yods in the first 4 enfolded polygons outside the root edge that do not coincide with the 3 Sephiroth on either side pillar of the Tree of Life.
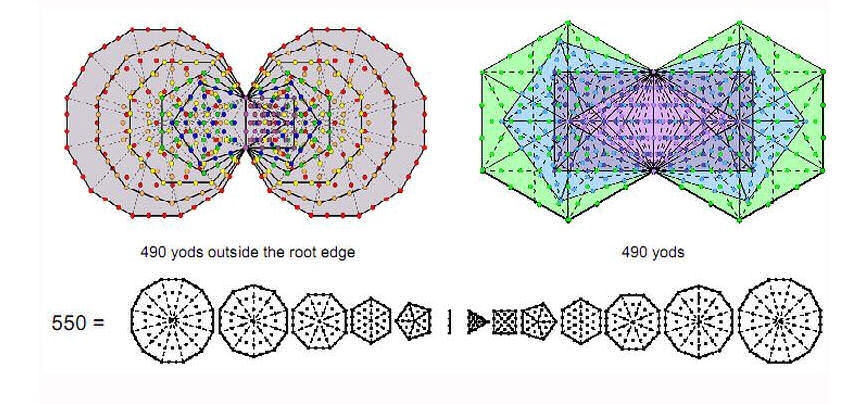
Figure 6. The first (4+4) enfolded Type B polygons have the same number (490) of yods as there are outside the
root edge of the (7+5) enfolded Type A polygons which, together with the root edge, separately have 550 yods.
-
There are (247–4=243) yods outside the root edge. Number of yods in the (4+4) enfolded polygons = 4 + 2×243 = 490 = 49×10, showing how EL CHAI, the Godname of Yesod with number value 49, prescribes the (4+4) enfolded polygons. This is also the number of yods outside the root edge of the (7+5) enfolded polygons which, separately and together with the four yods of the root edge, have 550 yods that symbolize the 550 SLs of CTOL (Fig. 6) [1]. The 490 yods in the (4+4) enfolded polygons comprise 62 corners (31 corners associated with each set), 326 hexagonal yods on 163 sides of 102 tetractyses & 102 hexagonal yods at their centres, i.e., (326+102=428) hexagonal yods. (490−102=388) yods line their sides, 194 yods per set. 31 is the number value of EL, Godname of Chesed, 62 is the number value of its Archangel Tzadkiel, 428 is the number value of Chasmalim, its Order of Angels and 194 is the number value of Tzadekh, the Mundane Chakra of Chesed. Here is a remarkable example of how the number values of the same Sephirah in the four Kabbalistic Worlds of Atziluth, Beriah, Yetzirah and Assiyah measure properties of an object possessing sacred geometry.
The (7+7) enfolded Type B polygons of the inner Tree of Life have 1370 yods [2]. The last (3+3) enfolded polygons have (1370−490=880) yods outside the root edge. 880 = 88×10, where 88 is the 87th integer after 1 and 87 is the number value of Levanah, the Mundane Chakra of Yesod. They have 50 corners (48 outside the root edge), where 50 is the number of ELOHIM and 48 is the number of Kokab, the Mundane Chakra of Hod. The last 3 enfolded polygons have 26 corners, where 26 is the number value of YAHWEH.
10
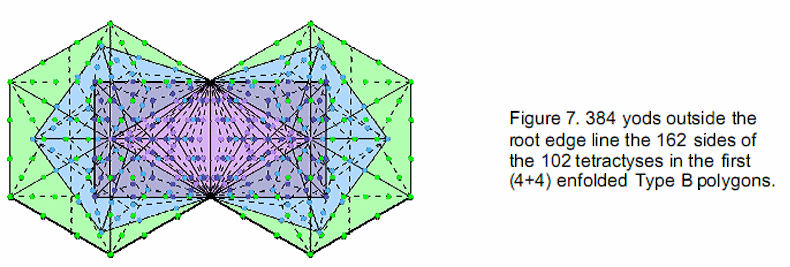
-
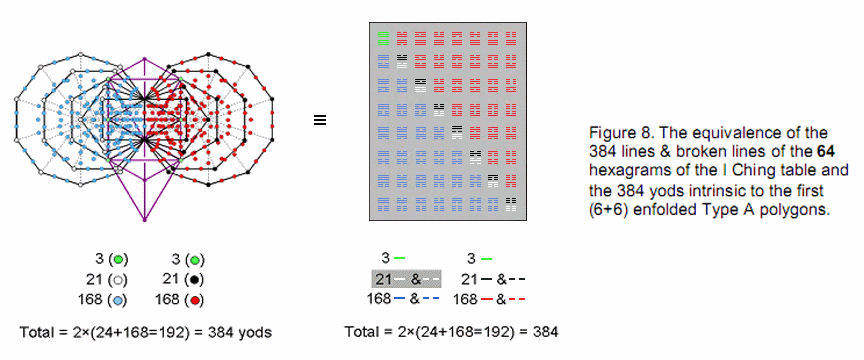
As the (4+4) enfolded Type B polygons have 102 tetractyses, each with a hexagonal yod at its centre, there are (490–102=388) yods lining their 163 sides. (388–4=384) yods outside the root edge line 162 sides, 192 in each set (Fig. 7). This 192:192 division is another characteristic of holistic systems, being found, for example, in the 192 lines and 192 broken lines making up the 64 hexagrams used in the ancient Chinese system of divination known as I Ching and in the 192 yods associated with each set of the first six enfolded polygons and unshared with polygons enfolded in the next higher Tree of Life (Fig. 8). 24 yods line the nine sides of the triangle, square & pentagon. They correspond to the 24 lines & broken lines in the upper or lower trigrams in the eight hexagrams forming the diagonal of the 8×8 square array of hexagrams and to the 24 corners associated with each set of the first six enfolded polygons unshared with the polygons enfolded in the next higher Tree of Life. The remaining 168 yods correspond to the 168 lines & broken lines in the 28 off-diagonal hexagrams in either diagonal half of the array and to the 168 yods in the first six enfolded polygons that are not corners of polygons.
The number 384 is the sum of the first nine squares after 1:
384 = 22 + 32 + 42 + 52 + 62 + 72 + 82 + 92 + 102.
It illustrates the fundamental connection between the Pythagorean Decad and this measure of holistic systems represented by sacred geometries.
3. How the Godnames prescribe the first four polygons
Set out below is a summary of the way in which the Godnames of the 10 Sephiroth prescribe the first four polygons and the (4+4) polygons:
| Sephirah |
Godname
|
Properties |
| Kether | EHYEH = 21 |
22 corners of first (4+4) enfolded polygons, where 22 = 21st integer after 1. |
| Chokmah | YAH = 15 | 15 sides of first 4 enfolded polygons; 15 corners of 17 sectors of first 4 enfolded Type A polygons. |
| YAHWEH = 26 | 26 corners outside root edge of 34 sectors of first (4+4) enfolded Type A polygons. | |
| Binah | ELOHIM = 50 |
51 corners & sides of 34 sectors of
first (4+4) enfolded Type A polygons, where 51 = 50th integer after
1. |
| Chesed | EL = 31 |
31 sides of 17 sectors of first 4 enfolded
Type A polygons. |
| Geburah | ELOHA = 36 |
36 corners/sides
of first 4 separate Type A polygons. |
11
|
360 (=36×10) geometrical
elements |
||
| Tiphareth | YAHWEH ELOHIM = 76 |
76 geometrical
elements in first 4 separate Type A polygons. |
| Netzach | YAHWEH SABAOTH = 129 |
130 corners & sides of 54 sectors
of first 4 separate Type B polygons, where 130 = 129th integer after
1. |
| Hod | EL ChAI = 49 |
153 geometrical
elements in first 4 enfolded Type B polygons other than their corners. |
| Yesod | EL ChAI = 49 | 49 intrinsic corners & sides of first (4+4) enfolded Type A polygons. |
| Malkuth | ADONAI = 65 |
130 corners & sides of 54 sectors
of first 4 separate Type B polygons, where 130 = 65th even integer. |
| ADONAI MELEKH = 155 |
155 geometrical
elements in root edge and in first (4+4) separate Type A polygons. |
4. The hexagon embodies the dimension 248 of E8
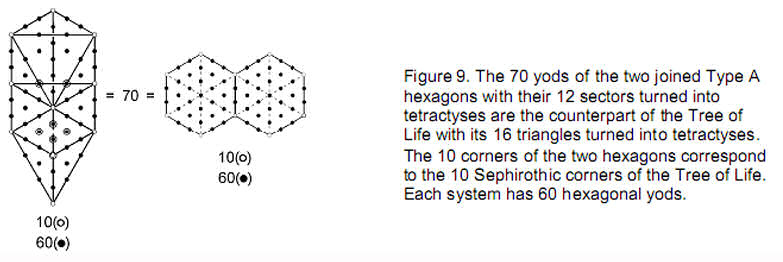
The pair of joined Type A hexagons has 70 yods when their 12 sectors are transformed into tetractyses. This is the number of yods in the Tree of Life when its 16 triangles are tetractyses (Fig. 9). The 10 corners of the two hexagons correspond to the 10 Sephirothic corners of the triangles making up the Tree of Life. Their 60 hexagonal yods are the counterpart of the 60 hexagonal yods in the latter. This correspondence suggests that the two joined hexagons are the single polygonal counterpart of the Tree of Life.
It should therefore not be surprising that they embody parameters of holistic systems, as we now show. The next level of transformation of the Type B polygon is the Type C polygon in which each triangle of the former is
12
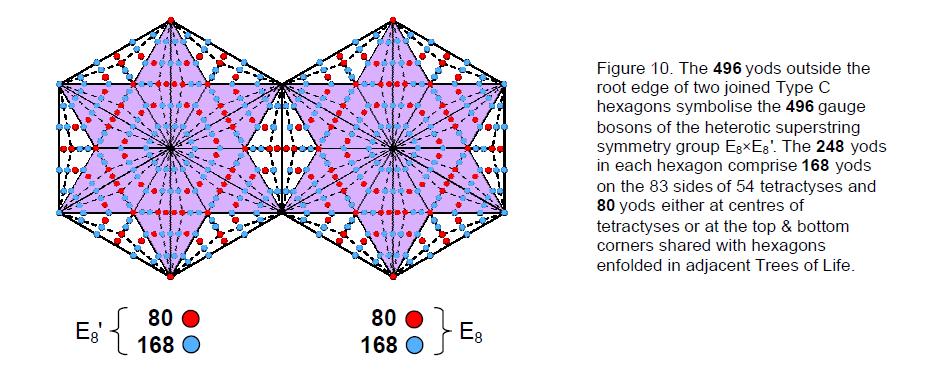
replaced by a Type A triangle. The Type C n-gon has (42n+1) yods. A Type C hexagon (n=6) has 252 yods surrounding its centre. (252–4=248) yods in each hexagon outside their root edge surround their centres (Fig. 10). 500 (=50×10) yods surround the two centres, 496 yods being outside the root edge, where 496 is the number value of Malkuth. This is how ELOHIM, the Godname of Binah with number value 50, prescribes the polygonal representation of the dimension 496 of E8×E8, one of the two gauge symmetry groups governing the unified interaction of heterotic superstrings.
E6 subgroup
Inside each sector of a Type C n-gon are 13 yods that are either corners of tetractyses or hexagonal yods at their centres. A Type C hexagon has (6×13=78) such yods. 78 is the dimension of E6, the rank-6 exceptional subgroup of E8. The six yods at the centres of each sector denote the six simple root of E6 and the 72 other yods denote its 72 roots. The top and bottom corners of the hexagon (those which are shared with the hexagons enfolded in the adjacent Trees of Life) denote the remaining simple roots of E8. The number 248 divides into 80 yods
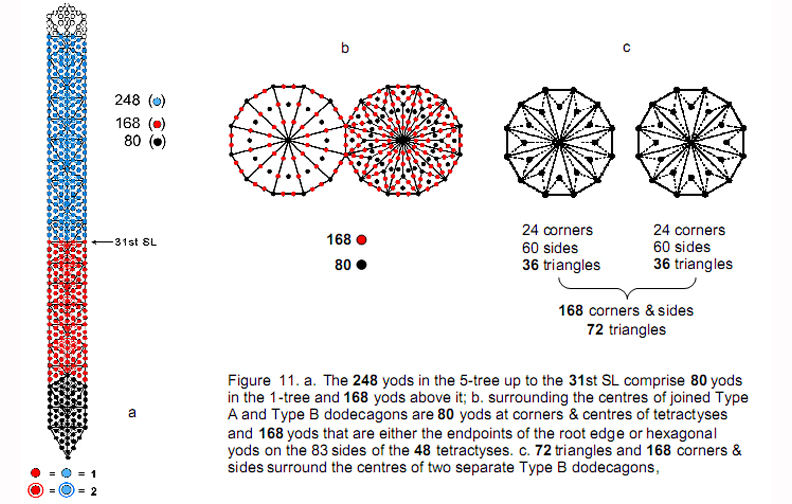
that denote the eight simple roots of E8 and the 72 roots of E6 and 168 yods denoting the 168 roots of E8 that are not roots of E6. This 80:168 division of the number 248, which is essentially the 72:168 division of the holistic parameter 240 discussed earlier, manifests in the context of the outer Tree of Life as follows: there are 80 yods in the 1-tree and 168 yods above it up to Chesed of the 5-tree, which is the 31st SL prescribed by the Godname EL of Chesed (Fig. 11a). It also appears in the dodecagons because joined Type A and Type B dodecagons have 80 yods at corners and centres of their 48 tetractyses and 168 yods that are either the endpoints of the root edge or hexagonal yods on the 83 sides of tetractyses (Fig 11b). The 72:168 division appears in a pair of separate Type B dodecagons as their 72 triangles and as the 168
corners & sides that surround their centres (Fig. 11c). It exists because, as the tenth type of polygon determined by the Decad, the dodecagon is a holistic object
13
that displays the characteristics of holistic systems. For example, 24 corners of triangles surround the centre of each separate Type B dodecagon, comparing with the 24 corners of the first six enfolded polygons on either side of the root edge with its two endpoints, the properties of these two sets of polygons being shown in Article 4 [3] to be prescribed by the Godnames of the 10 Sephiroth and to display properties characteristic of such systems. Another example is the fact that 168 more yods are needed to transform the 12 sectors of the dodecagon with 13
5. The hexagon embodies superstring structural parameters
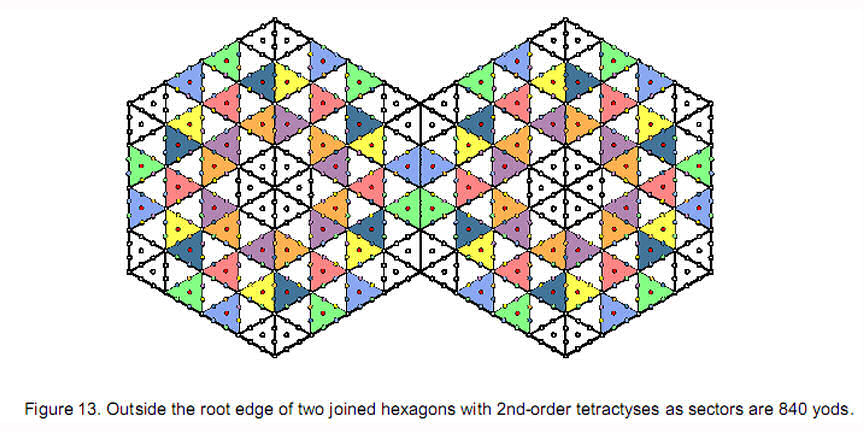
The number of yods in an n-gon with 2nd-order tetractyses as sectors is 72n + 1 [4]. A hexagon has 433 yods. Thirteen yods lie on an side, leaving 420 yods outside it. Two joined hexagons have 840 yods outside their root edge (Fig. 13). The two hexagons embody not only the
85 = 40 + 41 + 42 + 43.
This demonstrates how the Tetrad expresses the extra number of yods needed to construct a Type B
14
15
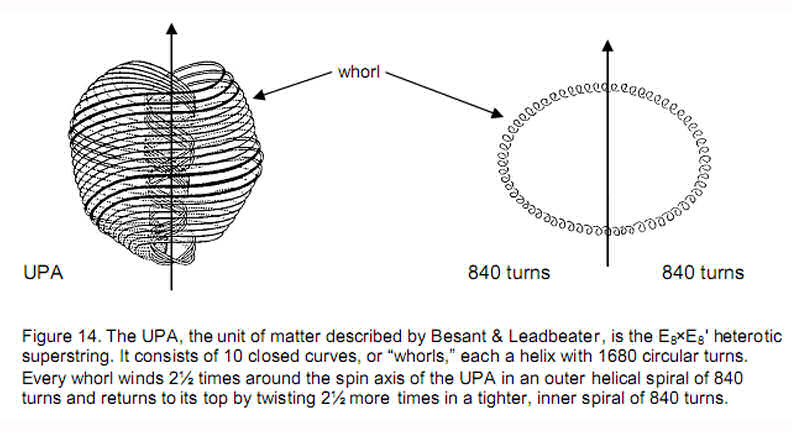
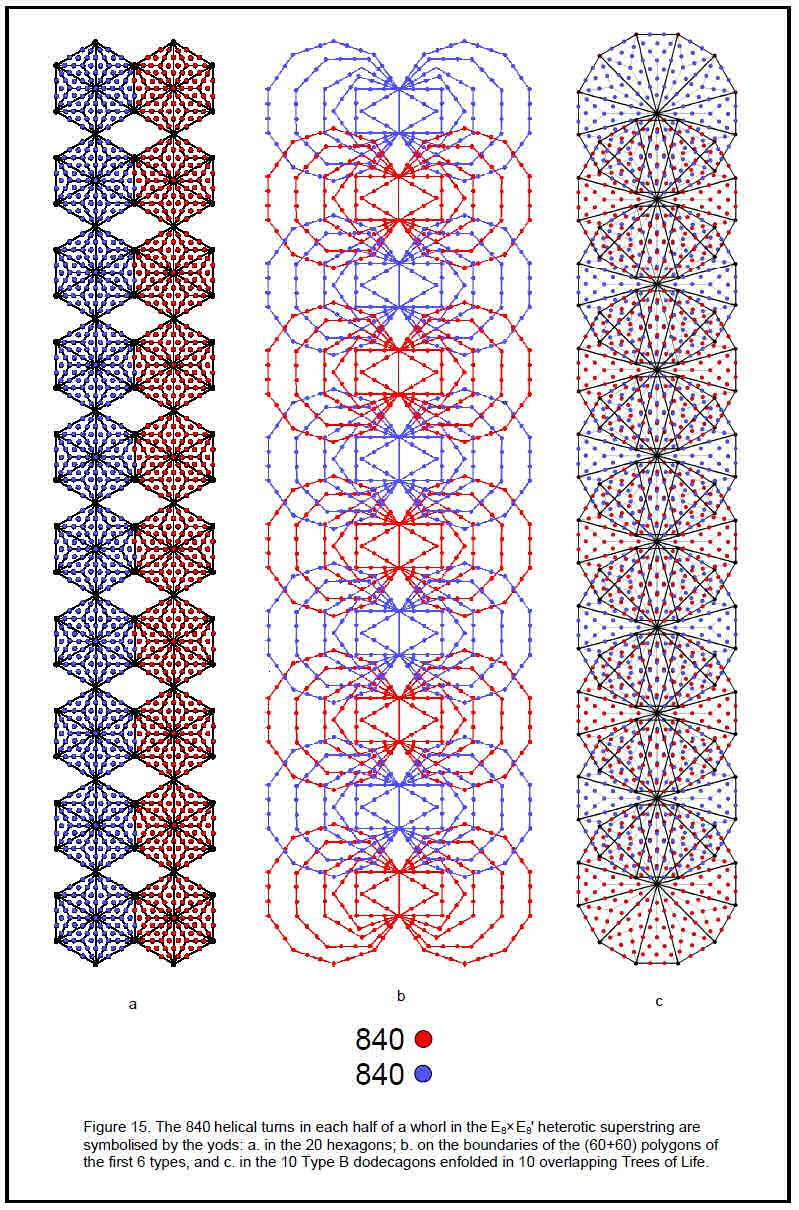
hexagon from 18 tetractyses. The two joined Type B hexagons therefore have 85 + 85 – 2 = 168 yods other than corners. 84 such yods are associated with each hexagon. Enfolded in 10 overlapping Trees of Life are 20 hexagons with (840+840=1680) yods other than corners (Fig. 15a). The same information is embodied in the first (6+6) polygons enfolded in 10 overlapping Trees of Life (Fig. 15b) because 1680 yods line their sides outside their root edges. It is also embodied in the 10 Type B dodecagons enfolded in 10 Trees of Life as the 1680 yods other than corners that surround their centres (Fig. 15c). Here are equivalent, holistic objects embodying the same information, namely, the number of circular polarized oscillations in each vibrating whorl. This structural parameter of the heterotic superstring is prescribed by ADONAI, the
Godname of Malkuth, because the lowest 10 overlapping Trees of Life have 65 SLs. This Sephirah is appropriate, as Malkuth signifies the outer, physical form of any holistic object.
The 840 yods other than corners associated with each set of hexagons enfolded in 10 overlapping Trees of Life have their counterpart in the polyhedral Tree of Life [6]. Its outer form is the disdyakis triacontahedron (Fig. 16), which has 62 vertices, 180 edges & 120 triangular faces. Surrounding any axis passing through two diametrically opposite vertices are 840 vertices, edges & triangles in each half of the polyhedron when the 180 interior triangles formed by its edges and centre are Type A triangles:
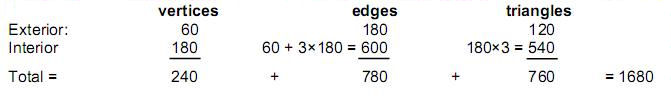
Moreover, when its exterior and interior triangles are turned into tetractyses, there are 840 yods surrounding the axis of the disdyakis triacontahedron:

As the hexagon is the fourth regular polygon, this is confirmation of the Tetrad Principle, which states that the fourth member of a class of mathematical object embodies numbers that are characteristic of holistic systems. It is the fourth member of a set of polygons that constitute a holistic system displaying properties
16
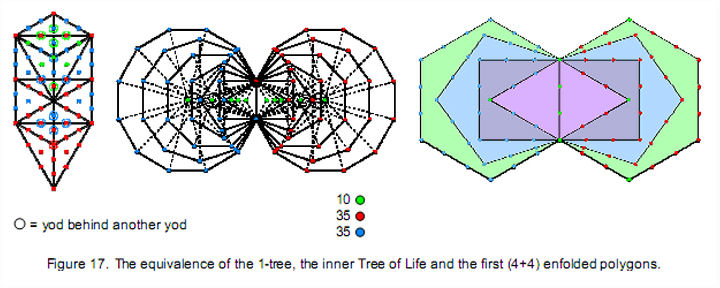
that are analogous to the Tree of Life. The most obvious example of this is that, as was found in the analysis of the yod composition of the first (4+4) enfolded Type A polygons, 80 yods line the sides of these polygons. This is the number value of Yesod and the number of yods in the 1-tree (Fig. 17) when its 19 triangles are turned into tetractyses, as well as the number of corners of the 94 sectors of the (7+7) enfolded polygons of the inner Tree of Life. The 35 red yods making up its ‘trunk’:
Point (Kether)
Line (Path connecting Chokmah & Binah)
Triangle ((triangle with Chesed, Geburah & Tiphareth at its corners)
Tetrahedron (tetrahedron with Netzach, Hod, Yesod & Malkuth at its vertices)
have their counterpart in the 35 red corners associated with one set of seven enfolded polygons and in the 35 red yods lining the outer sides of one set of the first four enfolded polygons, apart from the corner of the triangle and the top and bottom corners of the hexagon, which coincide with Sephiroth on the Pillar of Mercy of the Tree of Life, i.e., the 35 red yods are intrinsic to the four polygons themselves). The 35 blue yods making up the ‘branches’ of the 1-tree (the region outside its trunk) correspond to the 35 blue corners associated with the other set of seven enfolded polygons and to the 35 blue yods lining the outer sides of the other set of the first four enfolded polygons, apart from the corner of the triangle and the top and bottom corners of the hexagon, which coincide with Sephiroth on the Pillar of Judgement. The 10 green yods added by conversion of the Tree of Life with 70 yods into the 1-tree with 80 yods correspond to the 10 green centres of the (7+7) enfolded polygons that do not coincide with Sephiroth and to the 10 green yods in the first (4+4) enfolded polygons that either coincide with
Sephiroth or are in the root edge. Such natural, one-to-one correspondence with both the outer and inner forms of the Tree of Life is clear evidence that the first (4+4) enfolded polygons constitute what in previous articles has been called a “Tree of Life pattern” that embodies properties of holistic systems, such as the 248 gauge bosons that transmit the E8×E8'-invariant interaction between heterotic superstrings and the structural parameters 840 and 1680 of the E8×E8' heterotic superstring.
This conclusion about the holistic character of the first (4+4) polygons is given further support by the fact that the 108 triangles making up the first (4+4) separate Type B polygons have 80 corners (see comment 1 on page 6). They correspond to the 80 corners of the 94 sectors of the (7+7) enfolded Type A polygons (Fig. 18). The eight centres of the two sets of the first four polygons correspond to the eight corners of the latter that coincide with the positions of Daath, Tiphareth and the Sephiroth on the side pillars of the Tree of Life. The first (4+4) separate Type A polygons have 80 corners & sectors (see comment 8 on page 4). Truly, the Tetrad reveals here its power in defining members of classes of mathematical objects that have a holistic character because they are equivalent to, or embody properties of, the universal blueprint of the Tree of Life and other sacred geometries.
References
-
Phillips, Stephen M. Article 36: ”The Sri Yantra-like pattern of the 15 layers of vertices in the disdyakis triacontahedron and its scientific meaning,” (WEB, PDF), p. 10. Here is the proof that the (7+7) enfolded Type B polygons have 1370 yods:
|
triangle
|
square | pentagon | hexagon | octagon | decagon | dodecagon | |
| Number of yods = | 46 | 61 | 76 | 91 | 121 | 151 | 181 |
17
Of the 727 yods in the 7 separate polygons, the centre of the decagon coincides with a corner of the pentagon when they become enfolded. Fifteen yods in a sector of the hexagon disappear when it is replaced by the triangle in the enfolded set of polygons. (6×4=24) yods in the root edges of 6 polygons disappear when they become enfolded. Number of yods in the 7 enfolded polygons = 727 – 1 – 15 – 24 = 687. Number of yods in the (7+7) enfolded polygons = 687 + 687 – 4 = 1370.
-
Phillips, Stephen M. Article 4: “The Godnames prescribe the inner Tree of Life,” (WEB, PDF), p. 4.
-
Proof: a 2nd-order tetractys contains 85 yods. 13 yods lie along each side. Number of yods in an n-gon with its n sectors turned into 2nd-order tetractyses = (85–13=72)n + 1.
-
Besant, A, and Leadbeater, C.W. “Occult Chemistry,” 3rd ed., Theosophical Publishing House, Adyar, Madras, India, 1951.
- Phillips, Stephen M. Article 23: “The polyhedral Tree of Life,” (WEB, PDF).
18