| << Previous 1 [2] 3 4 5 ...10 Next >> |

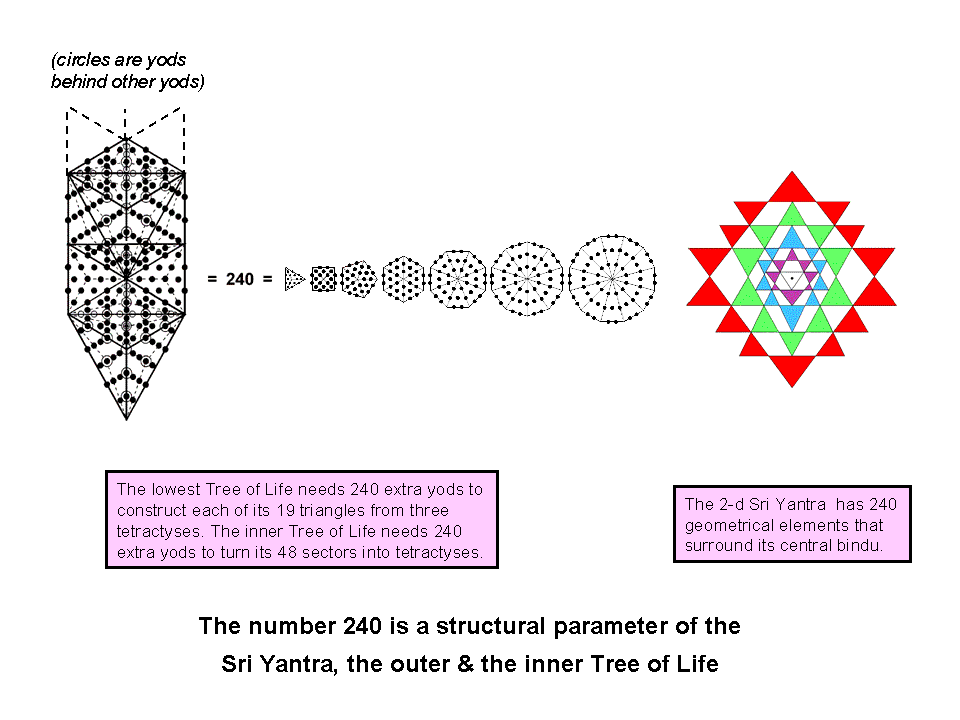
The number 240 was shown earlier to be embodied in the outer Tree of Life as the 240 extra yods required to build the 1-tree when the sectors of its 19 triangles are turned into tetractyses. It was shown to be embodied in the inner form of the Tree of Life as the 240 hexagonal yods in the seven separate regular polygons whose sectors are tetractyses. The 2-dimensional Sri Yantra also displays this parameter of holistic systems as the 240 points, lines & triangles that surround its centre (for proof, see page 8 of Article 35 (WEB, PDF). They are all counterparts of the 240 roots of E8, indicating that superstrings exist because their group symmetry is encoded in sacred geometries as an aspect of the Divine archetypes.
YAHWEH SABAOTH, the Godname of Netzach with number value 129, prescribes this geometrical counterpart of the 240 roots of E8 because the 43 triangles in the Sri Yantra have 129 sides.
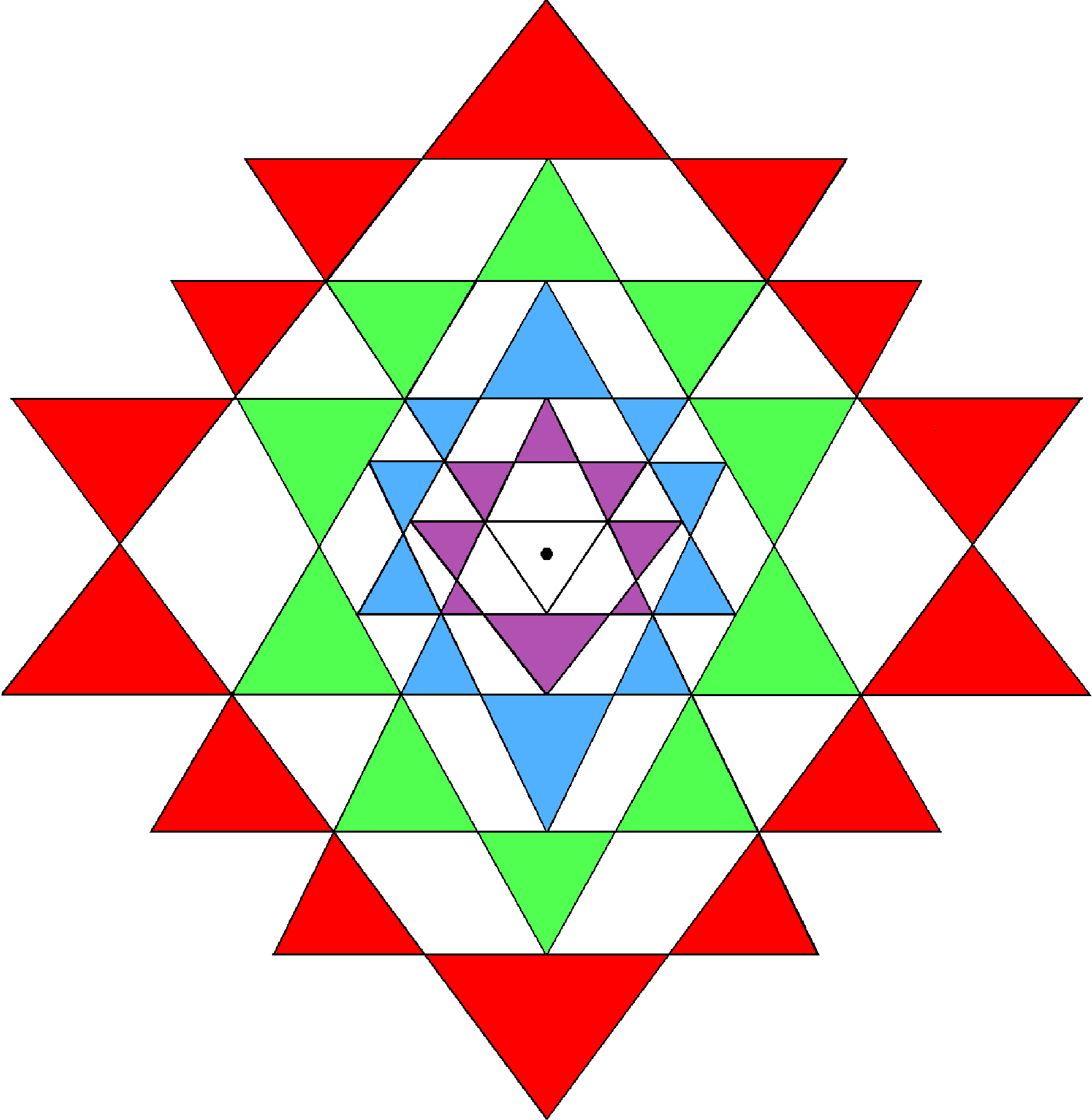
In the Tree of Life and Platonic solids subsections of Superstrings as sacred geometry, it was shown how these two sacred geometries embody the division of the 240 roots of E8 into the 72 roots of E6 and the remaining 168 roots. Let us see how this division manifests in the 240 geometrical elements surrounding the centre of the 2-dimensional Sri Yantra. Its geometrical composition is tabulated below (the bindu is excluded):
|
Points |
Number of sides |
Number of triangles |
Total |
|
| Central 'triangle' |
1 |
3 |
0 |
4 |
| 1st group of triangles |
4 + 8 = 12 |
8×3 = 24 |
8 |
44 |
| 2nd group of triangles |
6 + 10 = 16 |
10×3 = 30 |
10 |
56 |
| 3rd group of triangles |
2 + 10 = 12 |
10×3 = 30 |
10 |
52 |
| 4th group of triangles |
28 |
14×3 = 42 |
14 |
84 |
| Total |
69 |
129 |
42 |
240 |
Mathematically speaking, the central, downward-pointing triangle does not count as a true triangle because the bindu at the centre of the 2-dimensional Sri Yantra is a point that lies in its plane, so that this triangle consists only of three lines and three points, two of which coincide with corners of triangles belonging to the first group. The bindu is not to be thought of as merely one of the infinity of points making up the central triangle. It does not belong to this triangle, being the seed source of the creative energies of the triple Godhead, or trimurti, symbolised by the three corners of the triangle. The 42 triangles surrounding this centre have 126 sides, i.e., they comprise 168 lines & triangles. Including the lowest corner of the central triangle, there are 69 points surrounding the centre of the 2-dimensional Sri Yantra. Three straight lines form the central 'triangle.' Hence, the 240 points, lines & triangles that surround its centre comprise (69+3=72) points & lines and 168 lines & triangles. This is the counterpart of the similar 72:168 division manifested by the two separate sets of seven enfolded polygons making up the inner Tree of Life (72 corners and 168 hexagonal yods making up the 240 yods on their boundaries) and by the 240 hexagonal yods in the faces of the first three Platonic solids (see here). We shall see in the next section that it also appears in the disdyakis triacontahedron — the outer form of the Polyhedral Tree of Life. Notice that the 168 lines & triangles comprise the 42 triangles and the 42 lines in the fourth group of triangles, i.e., 84 lines & triangles, as well as 84 lines in the first three groups of triangles. This 84:84 division is characteristic of sacred geometries (see The holistic pattern). Its meaning vis-à-vis the UPA/superstring will be discussed next.
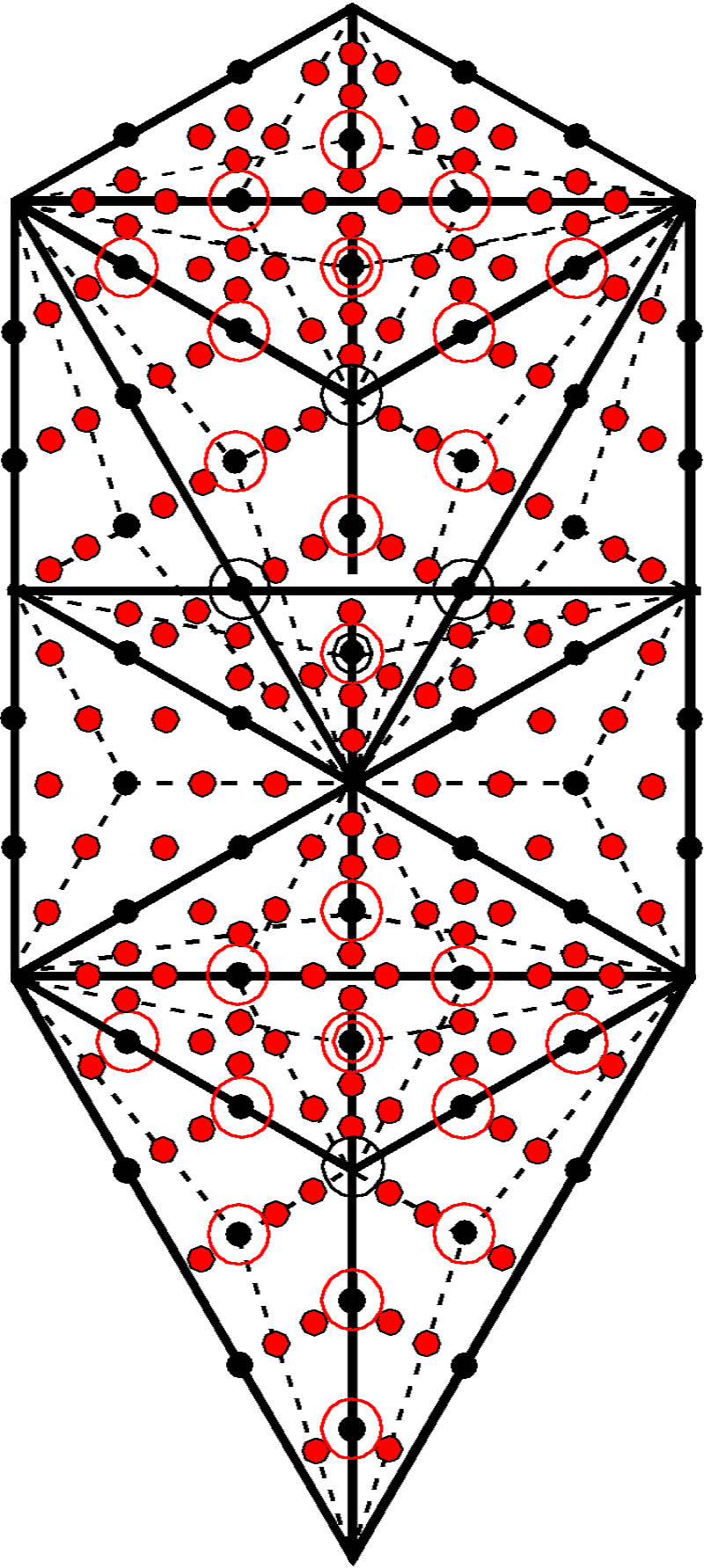
The 1-tree with tetractyses as its 19 triangles contains 80 yods, that is, (80−11=69) black yods other than the 11 corners of these triangles at which the 10 Sephiroth and Daath are located:
 |
 |
|
The 19 Type A triangles in the 1-tree consist of 69 black yods other than their corners and 171 red yods added by turning all the original triangles into Type A. |
69 points and 171 lines & triangles surround the bindu at the centre of the 2-d Sri Yantra. |
When they are turned into Type A triangles, they contain 251 yods, that is, 240 yods other these Sephirothic corners. They comprise the original 69 yods (coloured black in the diagram above) and 171 red yods added by turning the original triangles into Type A triangles. This 69:171 division appears in the 2-dimensional Sri Yantra (see table) as the 69 points (corners of triangles) and the (129+42=171) lines & triangles that surround the bindu at its centre.
When the Pythagorean integers 1, 2, 3 & 4 are assigned to the 73 yods in a Type A dodecagon, the sum of the 72 integers surrounding the central integer 1 is 240:
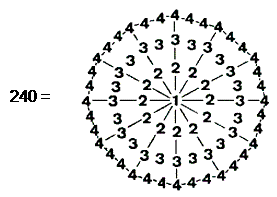
The integer 1, which the ancient Pythagoreans regarded not as a number but as the source of all numbers, calling it the Monad, denotes the bindu at the centre of the Sri Yantra. This point symbolises the Absolute, the source of all things. The 72 Pythagorean integers surrounding it add up to the number of corners, sides & triangles in the 2-dimensional Sri Yantra that surrounding the bindu. The dodecagon is the tenth type of regular polygon, showing how the Decad determines the number of geometrical elements that surround the centre of the Sri Yantra. When the bindu is included, the Decad determines the number 241 in an arithmetic way because it is the 120th odd integer after 1, where 120 is the sum of the first ten odd integers after 1:
120 = 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 +19 + 21.
241 is the 121st odd integer, where 121 = 112 and 11 is the tenth integer after 1. This is another way in which the Decad can be seen to determine the geometrical composition of the 2-dimensional Sri Yantra. Both the numbers 240 and 241 can be regarded as parameters of sacred geometries, for the combined outer & inner Trees of Life have 241 sides and triangular sectors of their Type A polygons when their shared root edge is included (see here), i.e., 240 sides & triangles are outside the root edge, just as the 2-dimensional Sri Yantra has 241 corners, sides & triangles when its central bindu is included, i.e., 240 corners, sides & triangles surround the bindu as its seed-like source.
| << Previous 1 [2] 3 4 5 ...10 Next >> |