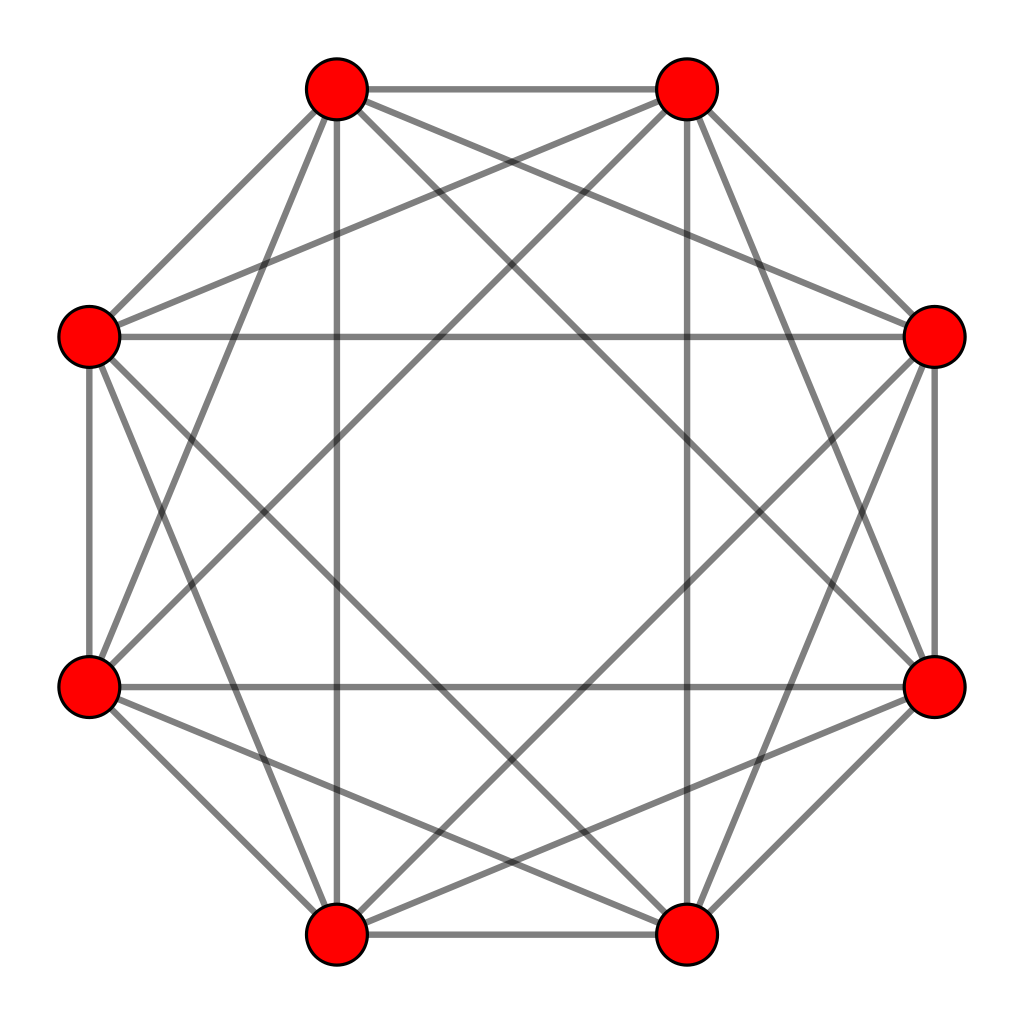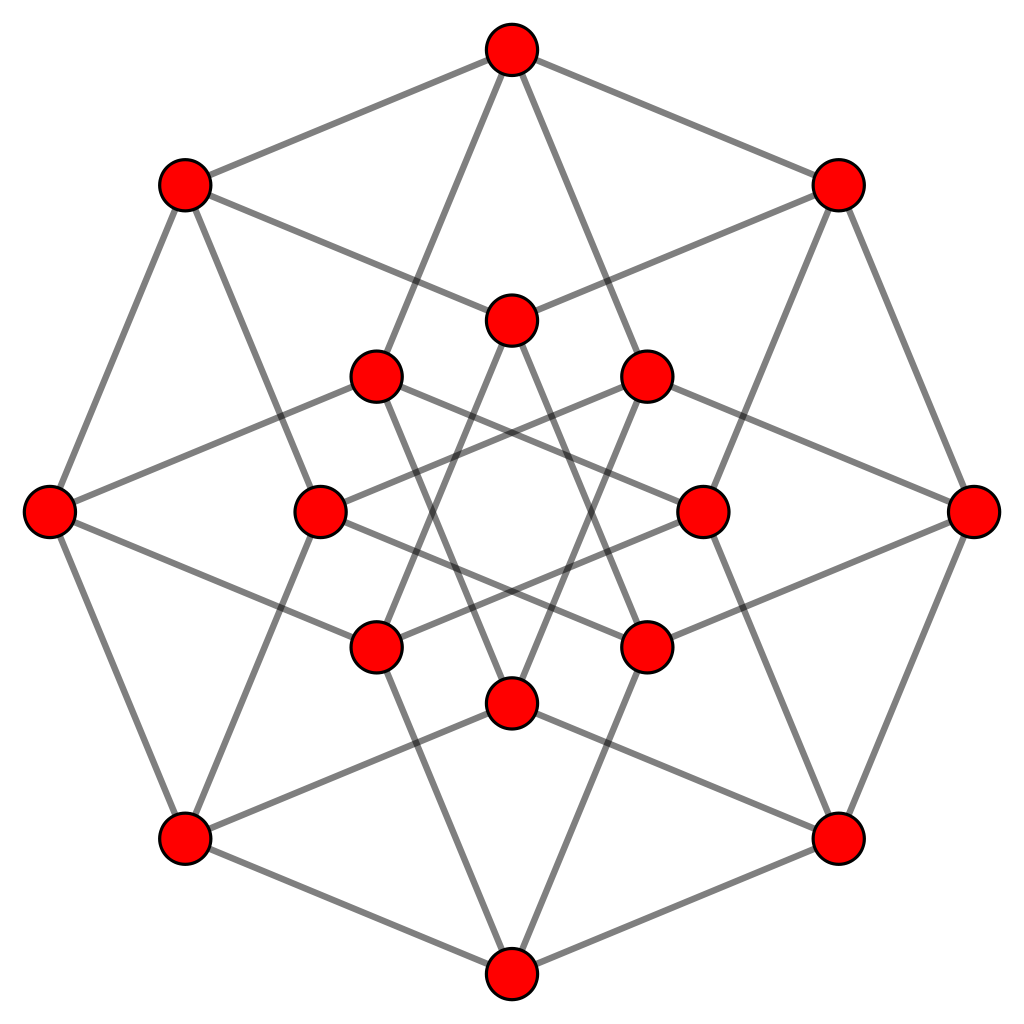
The 3 regular polygons absent from the sequence of 7 regular polygons that make up the inner form of the Tree of Life are the heptagon, nonagon & undecagon. When separate, they have 27 sectors with 30 corners & 54 sides. Enfolded, they have 27 sectors with 26 corners (24 outside the root edge), 25 external sides (24 outside the root edge) & 27 internal sides. As tetractyses, the sectors contain (5×27=135) hexagonal yods when separate and (135−2−2=131) hexagonal yods when enfolded (129 outside the root edge).
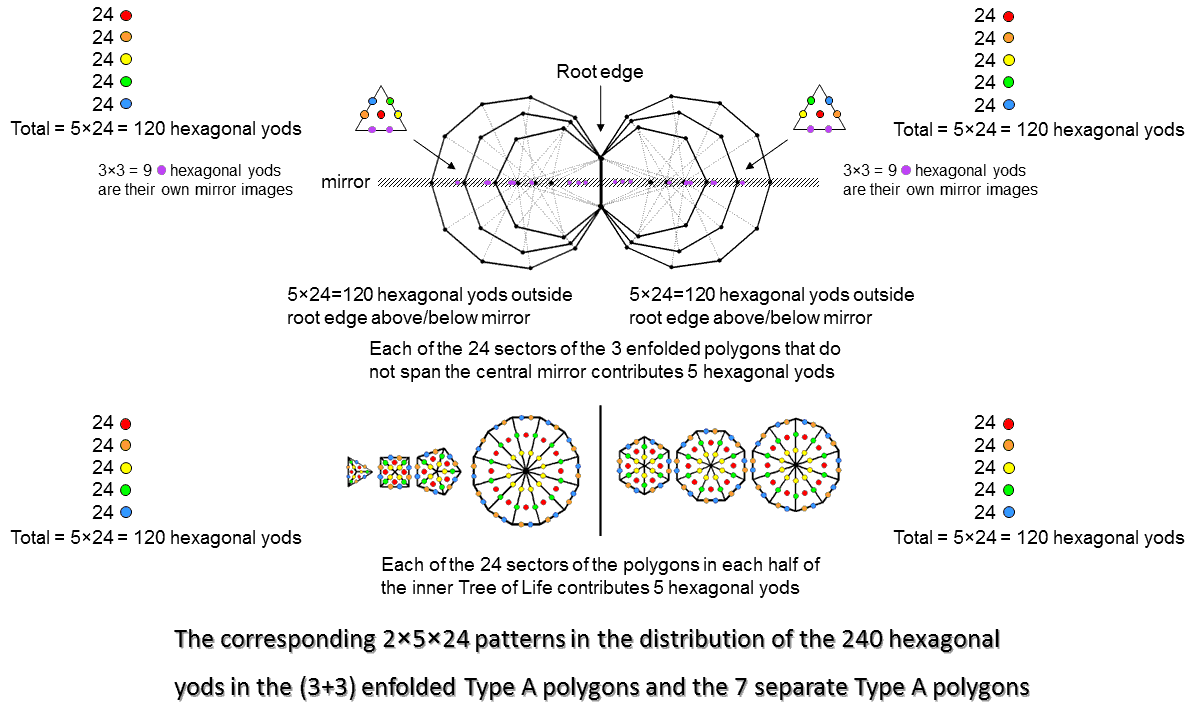
The 3 tetractys sectors sharing the root edge have a hexagonal yod (coloured violet in the diagram) at their centres that lies on the axis passing through the centres of the (3+3) enfolded polygons. Two violet hexagonal yods in each polygon line the internal side that lies on the axis diametrically opposite this hexagonal yod. If we imagine the axis as a mirror, then every yod in the upper half of a polygon has a counterpart in the lower half that is its mirror reflection. But yods lying on the axis are their own mirror images. So each polygon has 3 hexagonal yods that coincide with their mirror images. The number of hexagonal yods outside the root edge in each set of 3 enfolded polygons = 129 − 3×3 = 120. The (3+3) polygons have (120+120=240) hexagonal yods that have distinct mirror images. In each set of 3 polygons, there are 24 external sides outside the root edge, each lined by a pair of hexagonal yods, and 24 internal sides above and below the mirror, each lined by a pair of hexagonal yods. There are 24 tetractys sectors above and below the mirror, each with a hexagonal yod at its centre. The (2+2+1=5) hexagonal yods per tetractys sector are repeated 24 times over all the sectors. The (5+5=10) hexagonal yods per pair of sectors in the (3+3) enfolded polygons are repeated 24 times.
These 5×24 & 10×24 patterns are characteristic of sacred geometries. For example, see here, here & Article 53. The 7 regular polygons of the inner Tree of Life have two "halves": the triangle, square, pentagon & dodecagon with 24 sectors and the hexagon, octagon & decagon with 24 sectors. Constructed from tetractyses, the former half has 120 hexagonal yods (5 hexagonal yods per sector repeated 24 times) and the latter half has 120 hexagonal yods (5 hexagonal yods repeated 24 times). The two halves of the 7 types of polygons making up the inner Tree of Life have their counterpart in the two sets of the three absent polygons because both geometries display the 24:24 division in sectors that is characteristic of holistic systems. The (3+3) enfolded polygons actually have (27+27=54) sectors. But only (24+24=48) sectors have distinct mirror images, the 3 sectors in each set that straddle the mirror being mirror images of themselves.
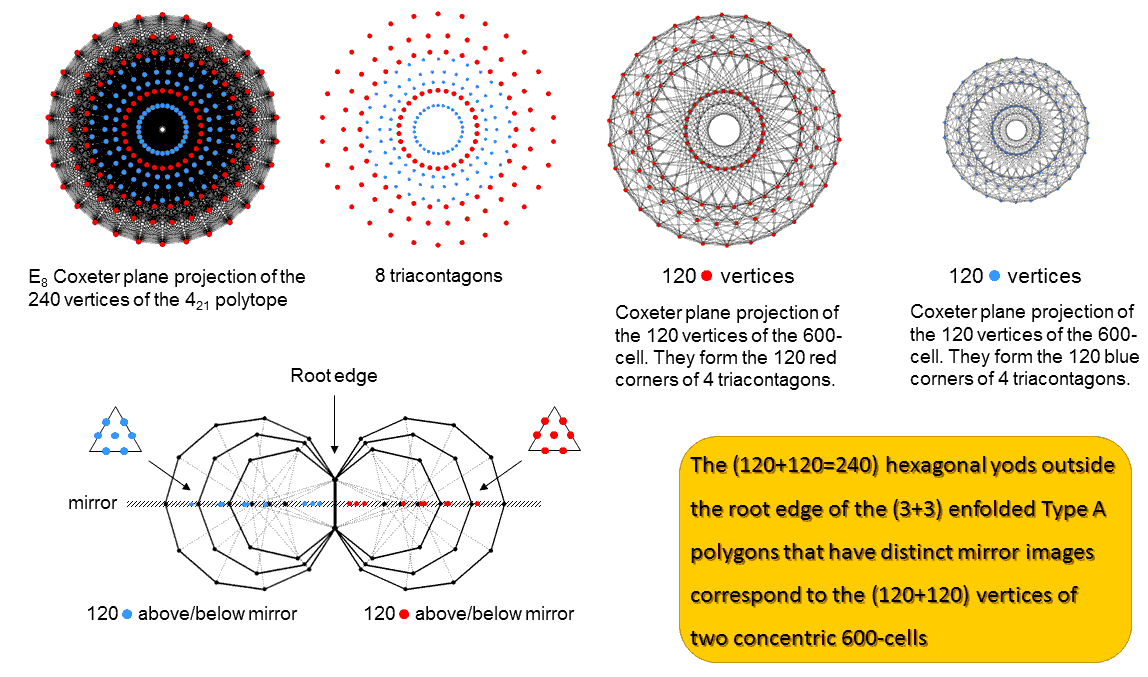
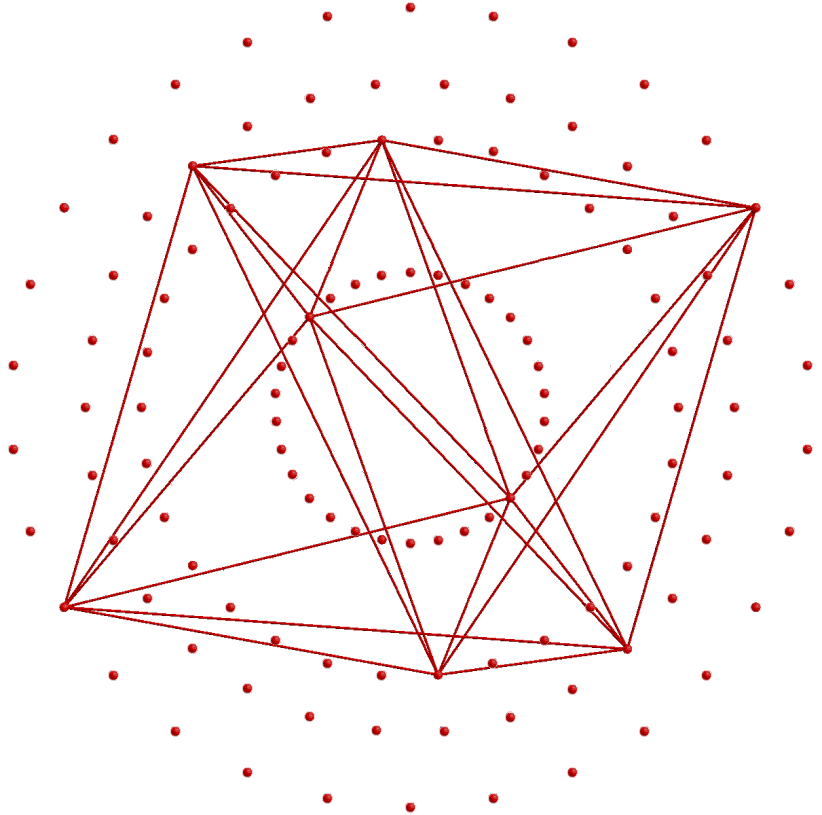
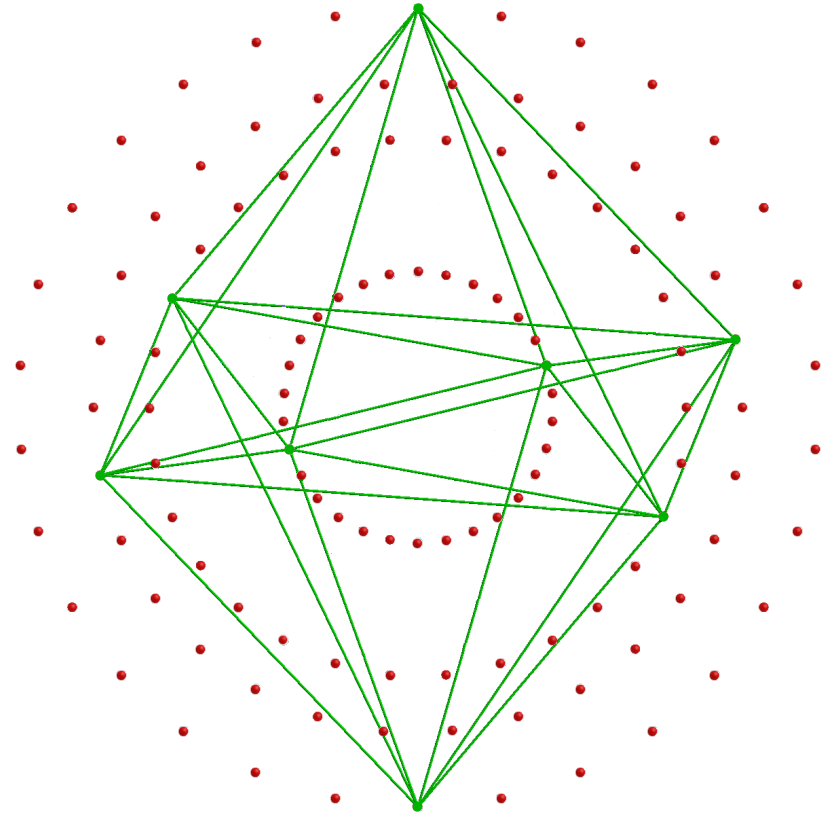
Article 62 analyses these 5×24 & 10×24 patterns in the polychoron composition of the 421 polytope. Their counterparts in sacred geometries are discussed in Article 53 and here. The E8 Coxeter plane projection of its 240 vertices consists of 8 concentric triacontagons with 30 corners. Four concentric triacontagons with 120 corners (denoted by red dots) are the H4 Coxeter plane projection of the 120 vertices of a 600-cell. Four smaller concentric triacontagons with 120 blue corners are the H4 Coxeter plane projection of the 120 vertices of a smaller 600-cell. This is because the Coxeter plane projection in 4 dimensions of the 240 vertices of the 421 polytope is a compound of two 600-cells. Amazingly, the (3+3) enfolded polygons display the same 120:120 division in their 240 hexagonal yods above and below their axis. Because of its inversion symmetry, every vertex in the 4-dimensional 600-cell with Cartesian coordinates (x1, x2, x3, x4) has its "opposite," or mirror image, with Cartesian coordinates (−x1, −x2, −x3, −x4). This is the reason for the requirement that every hexagonal yod should have a distinct mirror image; those that do not cannot denote vertices. One set of 3 polygons is the polygonal analogue of the larger 600--cell with 120 red dots representing its vertices and the other set is the counterpart of the smaller 600-cell with 120 blue dots representing its vertices. Their 120 hexagonal yods denote the vertices of each 600-cell. Just as the 60 hexagonal yods outside the root edge in the upper half of a set of 3 enfolded polygons have their mirror image counterparts in the 60 hexagonal yods in the lower half, so the 60 vertices in one half of the 600-cell have their inversions in the 60 vertices of its opposite half. The implication of their conformity to one of the characteristic patterns displayed by sacred geometries, namely, 240 = 120 + 120, is that the two sets of polygons absent from the inner Tree of Life contain, so to speak, the 2-dimensional seeds that grow into the 8-dimensional, 421 polytope whose 240 vertices represent the 240 roots of E8. Here in just 3 types of regular polygons is the beginning of the complete, mathematical symmetry of the forces between E8×E8 heterotic superstrings. The complex geometry of an 8-dimensional object has been reduced to that of three particular polygons because they are the precursor of the 2-polytopic form of the inner Tree of Life, of which the 421 polytope is the 8-polytopic version.
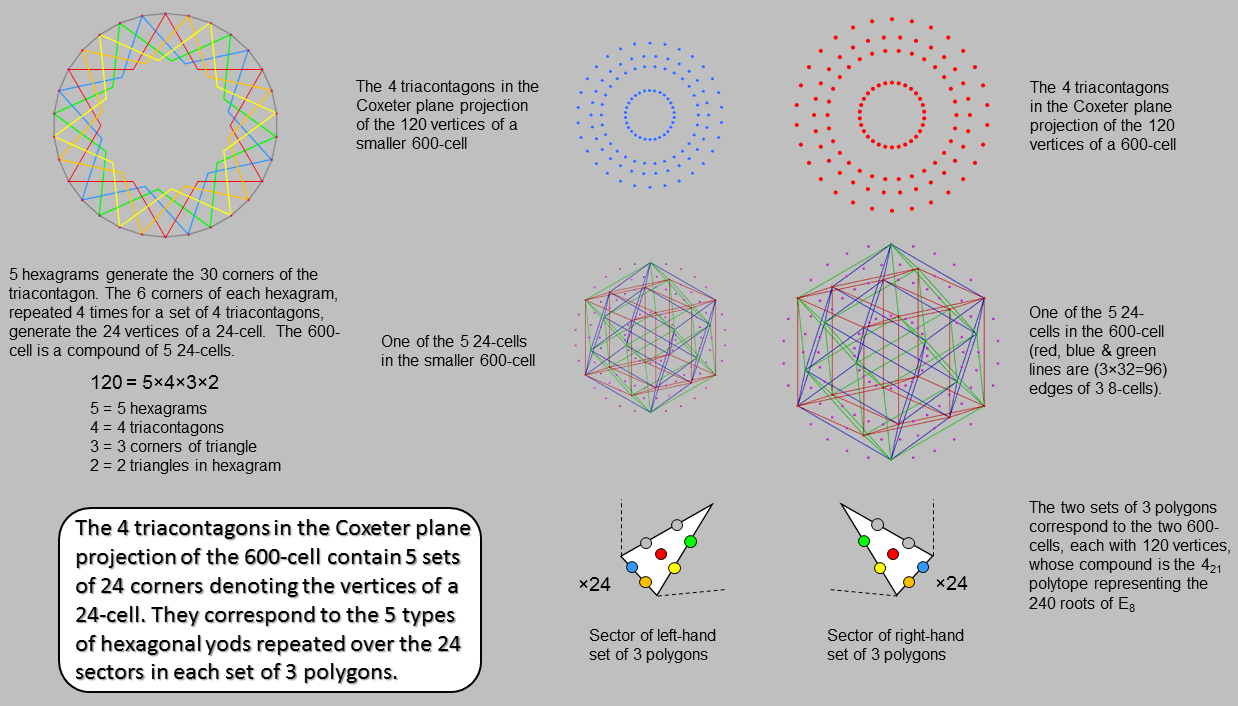
As 30 = 5×6, a triacontagon with 30 corners is generated by 5 hexagrams (coloured red, orange, yellow, green & blue), a hexagram being composed of 2 overlapping, equilateral triangles, each with 3 corners. The 4 triacontagons in the H4 Coxeter plane projection of a 600-cell with 120 vertices have 120 corners, where 120 = 5! = 5×4×3×2×1. We see that this factorisation has a simple, geometrical origin. The factor of 5 arises because a 600-cell is a compound of 5 24-cells, each with 24 vertices that correspond to the corners of a single hexagram in each triacontagon. Each 600-cell occupies a 4-dimensional subspace of the 8-dimensional space occupied by the 421 polytope. Its 4-dimensional Coxeter plane projection is a compound of two 600-cells, one smaller than the other. This means that it can be regarded as a compound of (5+5=10) 24-cells. The pair of sets of 3 enfolded polygons with(120+120=240) hexagonal yods is the counterpart of the pair of 600-cells with (120+120=240) vertices. There are 5 hexagonal yods per tetractys sector of a polygon. These 5 types of hexagonal yods are repeated 24 times over the 24 sectors of the heptagon, nonagon & undecagon that have distinct images reflected across the plane of the mirror in their axis. Similarly, the 5 types of hexagonal yods in the sectors of the second set of 3 polygons are repeated 24 times. Each type of hexagonal yod symbolises a vertex of one of the 5 24-cells. Its 24 repetitions correspond to the 24 vertices of a particular 24-cell. The 5:5 division of hexagonal yods and 24-cells corresponds in the outer Tree of Life to its 5 uppermost Sephiroth and its 5 lowest Sephiroth. Article 53 discusses the 10-fold (or, rather, double 5-fold) division in various sacred geometries. Article 62 discusses their relevance to the 10 disjoint 24-cells in the 421 polytope. The 120:120 division in the hexagonal yod populations of the (3+3) polygons is a characteristic pattern of all sacred geometries. It applies to the 24-cell itself, which has 24 vertices, 96 edges, 96 triangular faces & 24 octahedral cells. Its 240 0-, 1-, 2- & 3-polytopes comprise 120 vertices & edges and 120 faces & cells (see here). Its Petrie polygon is the dodecagon, the last in the sequence of the first 10 regular polygons. This confirms the holistic character of the 24-cell, which should come as no surprise, given that the 5:5 pattern of 24-cells in the Coxeter plane projection of the 421 polytope as a compound of two 600-cells is just the polytopic manifestation of the 5:5 division of the 10 Sephiroth of the Tree of Life.
24 = 8 +
16 = 8 + (3+5=8) + (3+5=8)
24 → 24 transverse dimensions of bosonic string.
Nonagon: 8 → 8 transverse dimensions of superstring.
Heptagon+undecagon: 16 → 16 bosonic string
dimensions.
Signature of transverse string dimensions in the 3 absent polygons
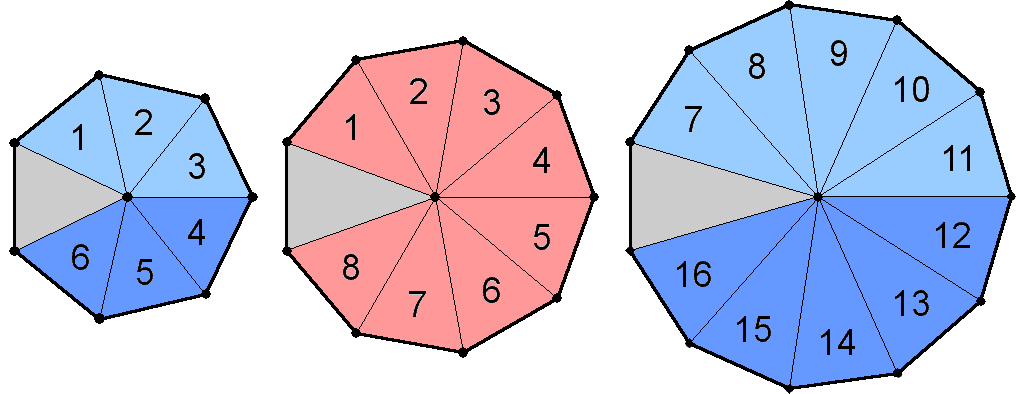
The grey sectors of the 3 polygons shown opposite are their own mirror images when reflected in the mirror lying in the axis joining their centres. The 24 sectors of each set of 3 polygons that have distinct mirror images comprise 6 in the heptagon (light blue & dark blue), 8 in the nonagon (red) and 10 in the undecagon (light blue & dark blue), i.e., 24 = 6 + 8 + 10. The counterpart of this in the 7 polygons with 48 sectors that make up the inner Tree of Life is that one of its "halves"* consists of the hexagon with 6 sectors, the octagon with 8 sectors and the decagon with 10 sectors. The 8:16 division appears also in the other half because the triangle & pentagon have 8 sectors, whilst the square & dodecagon have 16 sectors. The theory of spinless strings (so-called "bosonic strings") requires space-time to be 26-dimensional, so that they have 24 transverse dimensions, Superstring theory requires superstrings to have 8 transverse dimensions. As hybrids of superstrings and bosonic strings, heterotic superstrings have left-moving and right-moving excitations that are completely decoupled. The left-moving (anticlockwise) excitations are bosonic strings moving in 26 dimensions, whilst the right-moving (clockwise) excitations are 10-dimensional superstrings. Because of the isomorphism between N overlapping Trees of Life and the N tetractys sectors of an N-gon (see here), the 24 sectors of either the 3 polygons absent from the inner Tree of Life or each half of the set of 7 polygons that comprise it can be interpreted in terms of 24 overlapping Trees of Life. If these sectors can also denote dimensions of space transverse to the direction of motion of a string, then these Trees of Life can be understood as signifying such dimensions. It would indicate that the nonagon with 8 distinct, mirror-image sectors should be associated with the 8 transverse dimensions of superstrings and with the 8 dimensions of the root vector space of E8, whilst the heptagon & undecagon with 16 distinct sectors should be associated with the 16 higher, bosonic string dimensions. Notice that the 8 light blue sectors in the upper halves of these two polygons are mirrored by 8 dark blue sectors in their lower halves. This means that the 24 sectors of the 3 polygons naturally divide into 3 sets of 8. The significance of this is revealed below.
As the 3 enfolded polygons have 27 sectors with 26 corners (24 outside the root edge), their shapes symbolise the 26 dimensions of bosonic strings. The two endpoints of the root edge denote time and the longitudinal dimension, the 8 corners of the 9 sectors of the nonagon outside it denote the 8 transverse, superstring dimensions and the (6+10=16) corners of the 18 sectors of the heptagon & undecagon outside the root edge denote the 16 transverse, bosonic string dimensions.
* The two halves of the inner Tree of Life are discussed in Section 2 of Article 64.