| << Previous 1... 36 37 [38] 39 40 ...56 Next >> |
#38 10-fold geometrical composition of the disdyakis triacontahedron
Article 27 showed that, when both the internal triangles and the faces of the disdyakis triacontahedron are Type A triangles, 2400 corners, sides & triangles surround any axis passing through two diametrically opposite vertices (see Table 1, p. 4). It will now be proved that the 10-fold division of vertices & edges found above for this polyhedron extends to its total geometrical composition. In other words, these 2400 geometrical elements divide naturally into ten sets of 240 elements that divide further into three sets of 240 and seven sets of 240. The meaning of this 10-fold division is that, associated with the 240 roots of E8 are 240 vector gauge fields, each with ten components, so that 240 field components are defined by each of the 10 dimensions of superstring space-time. Each geometrical element making up the disdyakis triacontahedron that surrounds its axis bears a formal correspondence to a component of the 240 spin-1 gauge fields of E8.

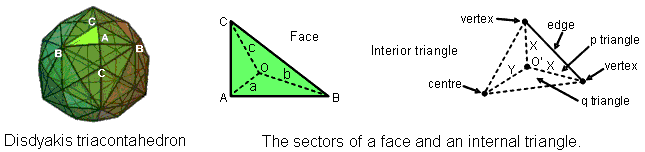
The adjacent diagram shows one of the 120 faces with centre O. Sides a, b & c are the internal sides of its three sectors that terminate, respectively, on A, B & C vertices. It also depicts an internal triangle with polyhedral vertices at two corners and the centre of the polyhedron at its third corner. The three sides meeting at O′ are of two types: one (X) that terminates on a vertex and one (Y) that ends at the centre. The three sectors of an internal triangle are of two types: one (p) that has a polyhedral edge as one side and two (q) that do not have an edge as a side. The edges are of three types: AB, BC & AC. The disdyakis triacontahedron has 180 edges, there being 60 edges of each type. Each one generates in an internal triangle two X sides & one Y side, one triangle of class p & two triangles of class q, as well as the centre O′. The table below shows the numbers of geometrical elements in the faces and interior of this polyhedron that surround its axis:
Numbers of corners, sides & triangles surrounding the axis of the disdyakis triacontahedron.

In the surface of the polyhedron are 120 triangular faces, each with three sectors with a, b & c sides, i.e., three sets of 120 sides of sectors and three sets of 120 sectors, i.e., three sets of 240 sides & triangles, or 720 (=72×10) geometrical elements. There are also 120 corners that are centres of faces and 60 vertices, as well as 60 sides joining the latter to the centre of the polyhedron. These form a set of 240 corners & sides. There are three sets of 120 X sides & 120 q triangles (indicated in orange, yellow & green), i.e., three sets of 240 geometrical elements, and there are three sets of 60 edges, 60 internal corners, 60 internal sides & 60 internal triangles (indicated in blue, indigo & violet), i.e., three sets of 240 elements. Hence, there are seven more sets of 240 geometrical elements. All these numbers, of course, refer to the geometrical elements that surround the axis.
We see that the 2400 geometrical elements
comprise ten sets of 240 that are made up of three sets of 240 sides & triangles in the faces and seven sets
that comprise two triplets of sets and a single set. This 3:3:3:1 pattern reproduces the pattern of Sephiroth
of the Tree of Life, which group into three triads and a final, single one:
Kether-Chokmah-Binah
Chesed-Geburah-Tiphareth
Netzach-Hod-Yesod
Malkuth
There are 720 elements in the faces that are unshared with the remaining 1680 elements. This pattern is the counterpart of the 72 roots of E6 and the 168 other roots of E8. The 1680 elements comprise 60 vertices & 180 edges, i.e., 240 elements in the faces, leaving 1440 elements, 720 elements belonging to each half of the disdyakis triacontahedron. The division:
1680 = 720 + 240 + 720
Is embodied in the 240 yods other than SLs in the 1-tree and in the 720 yods that surround the centres of each of the two sets of seven Type B polygons making up the inner Tree of Life (see diagram here). Every yod or geometrical element corresponds to a circular turn of each helical whorl of the UPA/subquark superstring. In other words, they denote circularly polarized oscillations of each whorl. The same division manifests in the compound of two 600-cells whose 240 vertices are the 4-dimensional projection of the 240 vertices of the 421 polytope (see here). This amounts to convincing evidence that the UPA is an E8×E8 heterotic superstring, for these 240 vertices define vectors that are identical to the 240 root vectors of the rank-8, exceptional Lie group E8. In other words, the 240 gauge charges of this symmetry group are spread along the 16800 turns of the 10 whorls of the UPA.