The polygonal Godhead Part 13

As we have just seen, the Godnames of the 10 Sephiroth mathematically prescribe the geometrical and yod composition of the three regular polygons that are absent from the inner form of the Tree of Life. Discounting the absurdity that this could be due to chance implies that the analogy between the 3:7 division of Sephiroth and the 3:7 division in the first 10 types of polygons is more than just a formal one. The three absent polygons must, together, constitute a holistic system. This means that they should express the basic pattern that is characteristic of such systems, as discussed at length in The holistic pattern. This will be verified later.

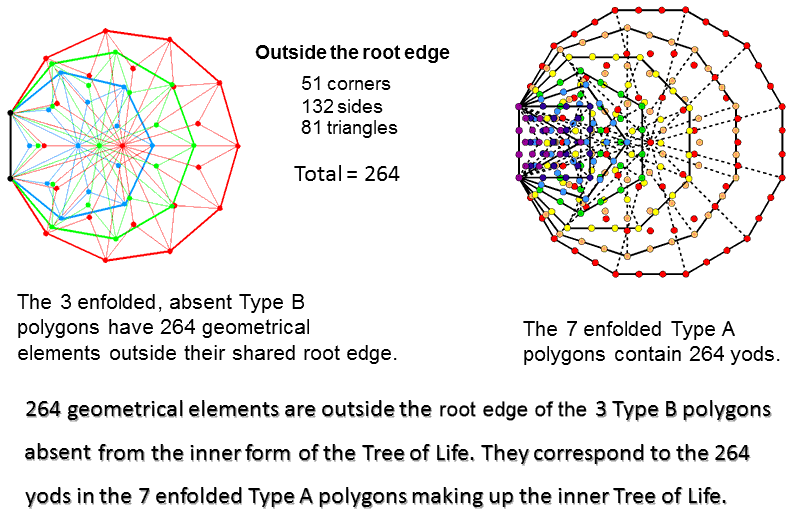
As a remarkable example of how the three polygons display holistic parameters, Table 2 indicates that they comprise 267 corners, sides & triangles when enfolded and Type B. Therefore, (267−3=264) geometrical elements are outside their root edge. This number is embodied in the inner Tree of Life as the 264 yods in the 7 enfolded Type A polygons constructed from tetractyses:

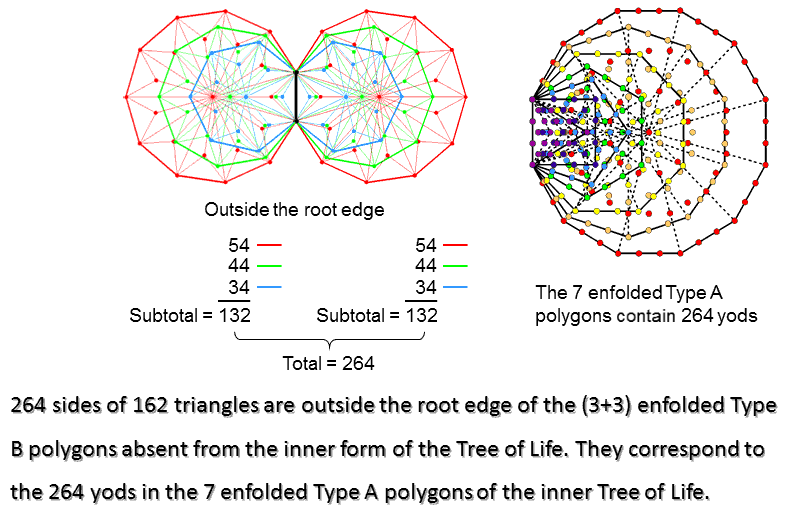
According to Table 2, the three enfolded polygons have 133 sides, so that the 264 geometrical elements include 132 sides and 132 corners & sides. This 132:132 division corresponds in the 7 enfolded Type A polygons as the 132 yods in the triangle, square, pentagon & dodecagon outside the root edge and the 132 yods in the hexagon, octagon & decagon (see Table 5 in Article 64). Outside the root edge of the (3+3) enfolded Type B polygons are (132+132=264) sides of (81+81=162) triangles. This is another way in which the (3+3) enfolded polygons embody a Tree of Life parameter.

Sacred geometries (including the 64 hexagrams used in the I Ching system of divination) display the following pattern of numbers:

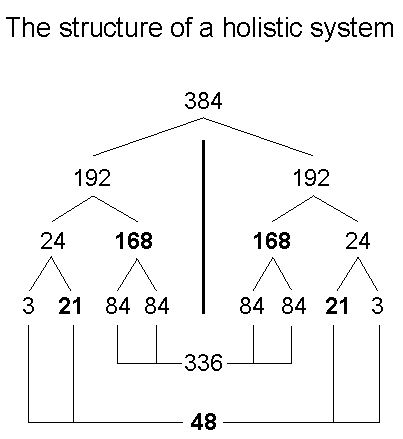
It is illustrated widely throughout this website. Inspection of Table 2 reveals that the three separate Type B polygons have 192 corners & sides. This means that the two sets of three separate Type B polygons (one set the mirror image of the other) have (192+192=384) corners & sides. The counterpart of this in the (7+7) separate Type A polygons is the (192+192=384) corners, sides & triangles that surround their centres:

Above and below the horizontal axis passing through the centres of each set of three polygons are 24 corners (12 black, 12 white). This leaves 33 red or blue corners and 135 red or blue sides, i.e., 168 corners & sides. This 24:168 division in the number 192 is a primary feature of this parameter of holistic systems. It exists in the seven separate Type A polygons as the 24 geometrical elements surrounding the centre of the hexagon (the fourth regular polygon) and the 168 geometrical elements surrounding the centres of the six other polygons when they are all divided into sectors. The 3:21 division in each set of 24 corners manifests as the three corners (black or white) in the heptagon above or below the axis and the 21 other corners. The 84:84 division of 168, which, as many pages in this website reveal, emerges as fundamental to the 3-dimensional structure of E₈×E₈ heterotic superstrings, manifests in the three separate polygons as follows: the 27 sectors of each set of three polygons have 54 sides and 27 internal corners, totalling 81 sides & corners. Including the three centres, there are 84 internal corners & sides of 27 sectors. The three triangles in a sector have three internal sides, so that the 81 triangles have 81 more internal sides. Including the three corners on the axis, there are 84 internal sides & corners. Hence, the 168 corners & sides consist of 84 internal corners & sides and 84 more corners & internal sides.

The number of yods in an n-gon with 2nd-order tetractyses as its sectors = 72n + 1, where "1" denotes its centre. The number of yods in the three separate polygons with 27 corners = 3 + 72×27 = 1947. Construction of the three polygons with 27 corners from 2nd-order tetractyses requires (1947−27=1920=192×10) more yods. The holistic parameter 192 is embodied in each set of three polygons as the number of yods in 192 tetractyses needed to transform their sectors into 2nd-order tetractyses. The number 1920 can be represented as a five-fold array of the squares of the nine integers 2-10:

Noting that 13 yods line each side of a 2nd-order tetractys, the number of yods in the three enfolded polygons with 2nd-order tetractyses as their sectors = 1947 − 13 − 13 = 1921. This can be represented by a five-fold array of the squares of the 10 integers 1-10, with 1² at its centre. It is composed of 46 squares. This beautiful property reveals the hidden role of the Decad (10) in determining parameters of the three polygons associated with the Supernal Triad.

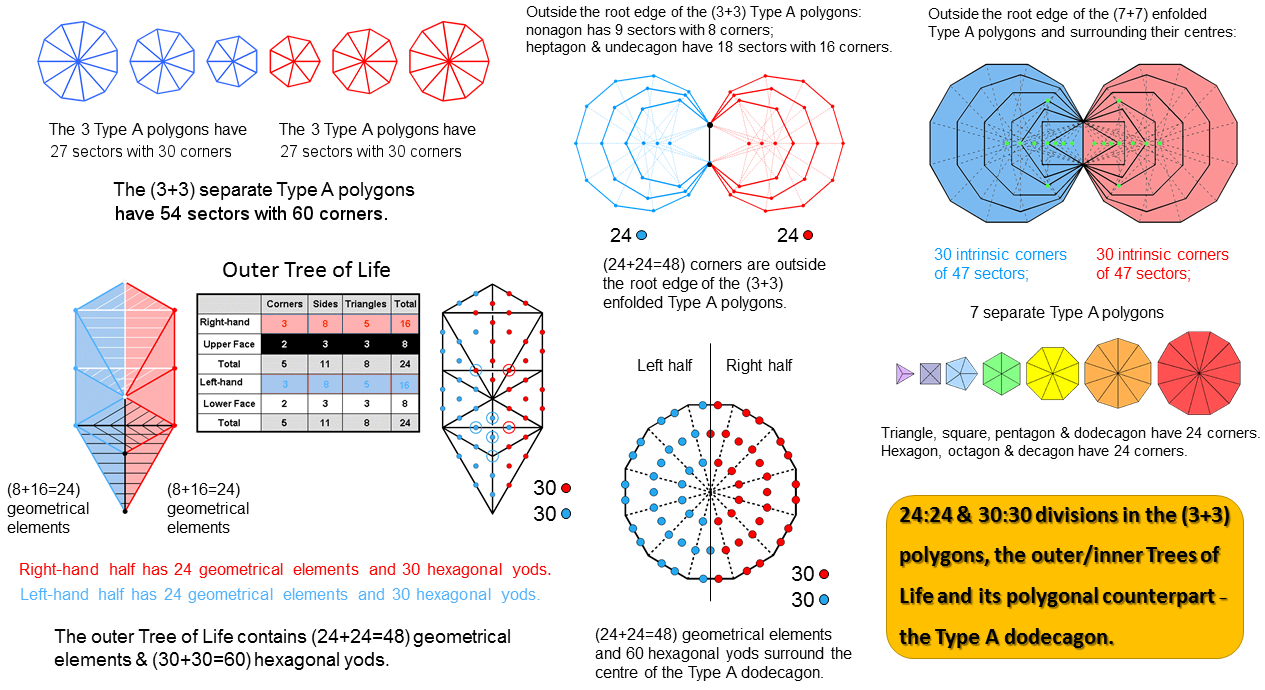
As a holistic system, the three polygons absent from the inner Tree of Life embody the various mathematical patterns displayed by the outer Tree of Life. This is illustrated below:

Intuitively, this is what should be expected, given that the seven Sephiroth of Construction emanate from the Supernal Triad, so that the various patterns within the seven polygons that represent the former should have originated from analogous patterns within the three polygons that represent the latter. The following comments are required:

The three separate Type A polygons have 27 corners and their 27 sectors have (27+3=30) corners. Both sets of polygons have (27+27=54) sectors with (30+30=60) corners. Compare this with the 60 hexagonal yods in the 16 triangles composing the outer Tree of Life when they are tetractyses. If we image a mirror aligned with the central Pillar of Equilibrium, its plane being perpendicular to the plane passing through the two side pillars, every hexagonal yod in the right-hand half has a mirror image in the left-hand half. But 12 hexagonal yods are aligned with the Pillar of Equilibrium that divides the outer Tree of Life into two mirror-image halves, each with 24 hexagonal yods (coloured red or blue) and 16 geometrical elements (coloured red or blue) outside the mirror (see table). As the outer Tree of Life comprises 48 geometrical elements, (48−16−16=16) geometrical elements do not have a separate mirror image because they are their own mirror image. Can these 12 hexagonal yods and 16 geometrical elements be equally distributed so that two resulting "halves" of the outer Tree, each containing the same number (30) of hexagonal yods and the same number (24) of geometrical elements, can be defined? The table in the diagram shows that this is possible in a mutually consistent way if the eight geometrical elements (coloured white) spanning the kite-shaped Upper Face are associated with the right-hand half and the eight geometrical elements (coloured black) spanning the Lower Face are associated with the left-hand half. The 30:30 division of corners of sectors of the (3+3) Type A polygons re-appears in the Tree of Life as the 30 hexagonal yods making up each (suitably defined) "half". The 24 corners of sectors outside the root edge of the three enfolded polygons re-appears in the outer Tree of Life as the 24 geometrical elements making up each half. The 8:16 division of corners of the nonagon and the heptagon & undecagon re-appears in each half of the outer Tree of Life as the eight geometrical elements that are their own mirror image and as the 16 geometrical elements that have distinct mirror images.

The seven enfolded Type A polygons making up the inner Tree of Life have 47 sectors with 41 corners. The top and bottom of each hexagon coincide with corners of triangles belonging to the outer Tree of Life when it is superimposed on it. Surrounding the centres of the seven polygons are (41−7−2−2=30) intrinsic corners outside the root edge. Outside the root edge of the (7+7) enfolded Type A polygons are (30+30=60) intrinsic corners surrounding the (7+7=14) centres. This is the counterpart of the 30:30 division of corners in the (3+3) separate Type A polygons.

The seven separate polygons of the inner Tree of Life have 48 corners. The triangle, square, pentagon & dodecagon have 24 corners, as do the hexagon, octagon & decagon. This is the counterpart of the 24:24 division of corners outside the root edge of the (3+3) enfolded Type A polygons.

The dodecagon is the polygonal counterpart of the outer Tree of Life. The Type B dodecagon has 60 hexagonal yods and 48 geometrical elements surrounding its centre. Each half of the dodecagon has 30 hexagonal yods and 24 geometrical elements. These parallels exist because the dodecagon is the single, polygonal counterpart of the outer Tree of Life.

According to Table 2, the three enfolded Type B polygons have 400 yods. The number of yods lining their 81 tetractyses = 400 − 81 = 319. The number of yods outside their root edge and surrounding their centres = 319 − 4 − 3 = 312. The (3+3) enfolded Type B polygons have (312×2=624) such boundary yods. The number of hexagonal yods in a 2nd-order n-gon = 13n. The seven Type B polygons in the inner Tree of Life with 48 corners have (13×48=624) hexagonal yods:

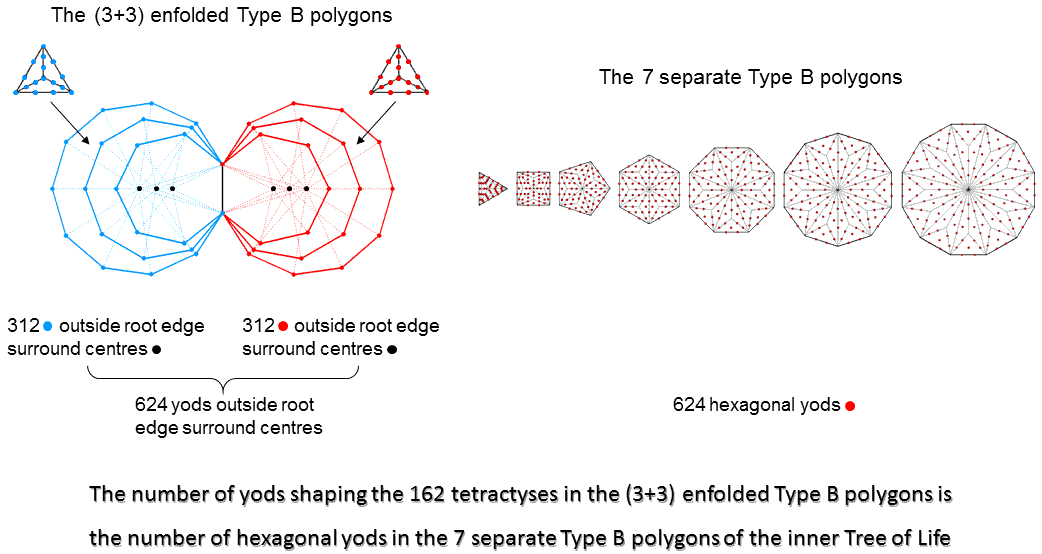The number of yods needed to shape the boundaries of the 162 tetractyses in the (3+3) enfolded Type B polygons is exactly the same as the number of hexagonal yods in the seven separate Type B polygons. Here is a spectacular example of how the archetypal numbers or holistic parameters embodied in the three polygons analogous to the Supernal Triad manifest in the polygons analogous to the seven Sephiroth of Construction. We may regard the three polygons in the first 10 polygons that are absent from the inner Tree of Life as their more abstract precursor. They are prescribed by the Godnames and embody patterns and numbers analogous to that found in sacred geometries because — despite their difference in appearance —they possess the miraculous property of being equivalent in a mathematical way to these geometries, e.g., the outer and inner Trees of Life. Of course, we mean 'remarkable,' not literally 'miraculous,' because there are perfectly simple, arithmetic reasons for this equivalence, as will be explained later.