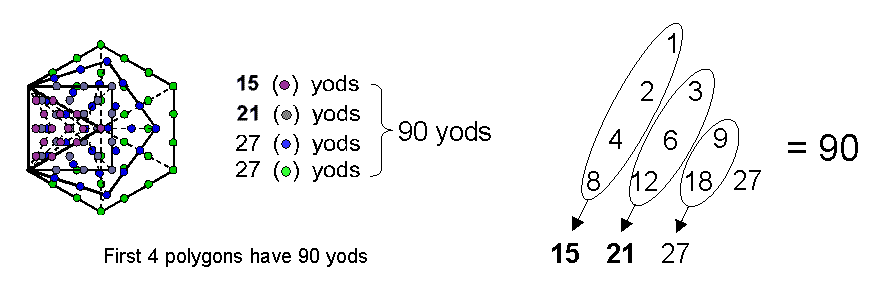
| << Previous 1... 6 7 [8] 9 10 ...16 Next >> |
The 90:260 pattern in the Tetrahedral Lambda and its counterpart in the inner Tree of Life
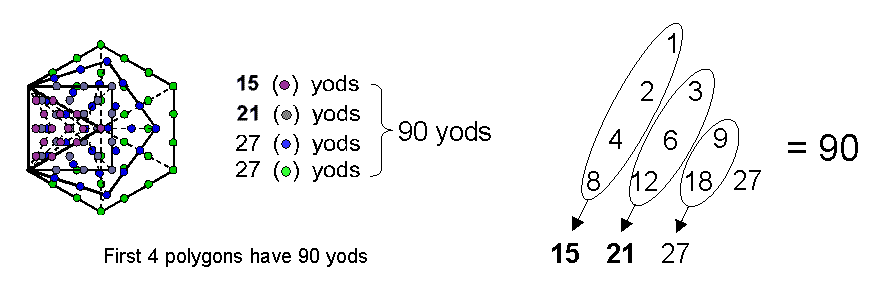
Figure 12. Correspondence between the Lambda Tetractys and the first 4 polygons.
Constructed from tetractyses, the seven enfolded polygons of the inner Tree of Life have 260 yods outside their shared side (see here). The first four polygons have 90 such yods (Fig. 12). Compare this with the Tetrahedral Lambda, whose 10 integers in its first face add up to 90 and whose 10 integers in its other three faces add up to 260. The analogy, of course, is not exact because the 90 yods are part of the set of 260 yods, whereas the sum 90 is not part of the sum 260 (none of the other faces has 10 integers adding to 90). The fact that the yod population of the first four polygons is 90 is an example of the Tetrad Principle at work. That their correspondence to the Lambda Tetractys is not coincidental is indicated by the remarkable fact that the yod populations of these individual polygons are the sums of the integers in the four right-slanting columns of numbers. What is more plausible: that this correlation, too, exists by chance or that a deep, mathematical harmony exists between different, but equivalent, holistic systems that enables their analogous features to manifest in such a clear way? Outside the shared side of the triangle and square are 36 yods; outside the shared side of the pentagon and hexagon are 54 yods. These two pairs of polygons are the respective counterparts of the numbers at the three corners of the Lambda Tetractys and at the centre and corners of the hexagon.
Article 48 proves the holistic nature of the two sets of the first four polygons.
The fourth regular polygon is the hexagon. 36 yods surround its centre when its sectors are tetractyses (Fig. 13). This becomes 90 yods (i.e., 54 yods are added) when its sectors are Type A triangles. The Tetrad Principle picks out the fourth, regular polygon as special, and, indeed, it is, becausethe Type B hexagon displays the 36:54 division characteristic of holistic systems. The number 6 at the centre of the Lambda Tetractys denotes the number of its corners, as one would expect, intuitively, because corners are shape-defining yods,
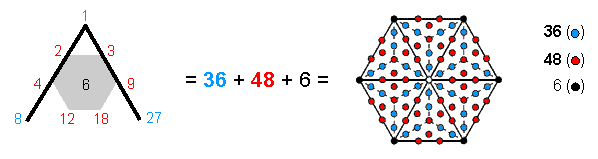
Figure 13. The equivalence of the Lambda Tetractys and the 90 yods surrounding the centre of the Type B hexagon.
a quality that is consistent with the meaning of Malkuth symbolized by the hexagonal yod at the centre of a tetractys and therefore with the number 6 occupying this position in the Lambda Tetractys. The 48 red yods correspond to the sum (48) of the six integers at the corners of the hexagon and the 36 blue yods correspond to the sum (36) of the integers at the corners of the Lambda Tetractys.
Another reason why the hexagon is special is the fact that a pair of joined hexagons have 70 yods when their 12 sectors are tetractyses (Fig. 14). 35 red yods are associated with one hexagon and 35 black yods are associated with the other. They correspond to the 35 corners associated with each half of the inner Tree of Life, as well as to, respectively, the 35 yods in the trunk of the Tree of Life and the 35 yods in its branches (see here; see here for definition of 'trunk' and 'branches'). The pair of hexagons can be regarded metaphorically as containing within them the 'seeds' (yods) that, when released, form the corners of the inner Tree of Life, i.e., generate its skeletal form. Just as the benzene molecule, the basis of organic chemistry, is hexagonal, so, too, is the polygonal counterpart of the Tree of Life.
The hexagon is the central polygon in the set of 15 polygons perpendicular to an axis passing through two opposite C vertices that are formed by the vertices of the disdyakis triacontahedron (see here). All its corners are A vertices. Surrounding the centres of these polygons are 840 yods other than polyhedral vertices that symbolise the 840 circularly polarised oscillations in each half of a whorl of the UPA/superstring (see here). 84 such yods, i.e., one-tenth of the total, are in the central hexagon. They symbolise the number of oscillations in a quarter-revolution of a whorl around the spin axis of the subquark/UPA. Notice that there are five 6-sided polygons and 10 triangles in the set of 15 polygons. This reflects the number value 15 of YAH (Hebrew: YH), because H (heh) has the number value 5 and Y (yod) has the number value 10. This is discussed in detail on page 10 of Article 44.
| << Previous 1... 6 7 [8] 9 10 ...16 Next >> |