Home

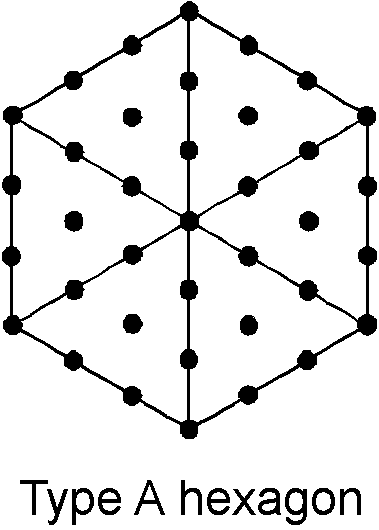
The hexagon

TYPE A HEXAGON

(1) The six-sided hexagon has 37 yods. 36 yods surround its centre, where 36 is the number value of ELOHA, the Godname of Geburah, which is the sixth Sephirah of Construction, counting from the bottom of the Tree of Life. Of these, 30 (= 1² + 2² + 3² + 4²) yods are hexagonal. 37 is the ratio

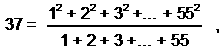
  where 55 is the tenth triangular number with a hexagonal representation in terms of the integers 1, 2, 3 & 4 symbolized by the four rows of the Pythagorean tetractys:

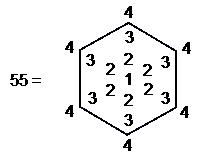
(2) The ratio

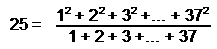
is the number of yods in a Type A square and the number of spatial dimensions of bosonic strings.
(3) The 37th odd integer is 73, the number of Chokmah. This defines the Godname number of Yesod:

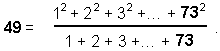
73 is the ratio:

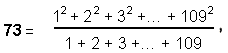
where 109 is the 55th odd integer. Since 55 is the tenth triangular number, the Pythagorean Decad determines arithmetically both the number of Chokmah and the Godname number of Yesod.
(4) Sum of first 37 integers = 703 = 37×19. Assigning these integers to the 37 yods in the hexagon, the sum of the 19 interior odd integers is 361 = 19². The interior of the hexagon arithmetically embodies the number of classical acupoints in the human body (see Article 32). Sum of 18 even integers on boundary = 342 = 18×19. Each sum is the number of yods generated by weighting each yod in the hexagon with the number of yods in a Type A triangle.
(5) Sum of squares of first 37 integers = 17575 = 37×19×25, where 19 and 25 are the numbers of yods in, respectively, a Type A triangle and a Type A square. Sum of squares of 19 interior integers = 9139 = 37×247, i.e., the sum of the weights 247 assigned to each yod in the hexagon. Therefore, the Type A hexagon arithmetically encodes the 247 yods lining the sectors of the seven separate Type A polygons. Sum of squares of 18 boundary integers = 8436 = 111×76 = 444×19, i.e., the sum of the weights 444 assigned to the 19 internal yods of the hexagon. The number 444 is the number of hexagonal yods in the (7+7) enfolded Type A polygons. The hexagon therefore encodes this Tree of Life parameter arithmetically.
(6) Arithmetic mean of first 37 triangular numbers is 247 (see above).
(7) Two enfolded hexagons contain 70 yods. Therefore, they encode the number of corners of the (7+7) enfolded polygons (see here) and the number of yods in a Tree of Life whose triangles are turned into tetractyses (see here).

TYPE B HEXAGON

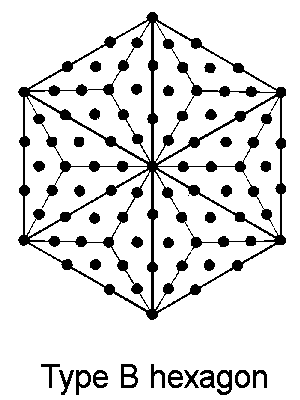The hexagon contains 91 yods, so the fourth, regular polygon encodes the number of Trees in CTOL. This shows how the Pythagorean Tetrad determines a fundamental number characterizing the spiritual cosmos. Indeed, the pattern of yods divides naturally into: 1. the 49 black yods that either line the six sectors or are hexagonal yods at centres of tetractyses, and 2. the 42 red yods that line their sides inside each sector. These two sets correspond, respectively, to the 49 subplanes of the cosmic physical plane and the 42 subplanes of the six cosmic superphysical planes (see also here):

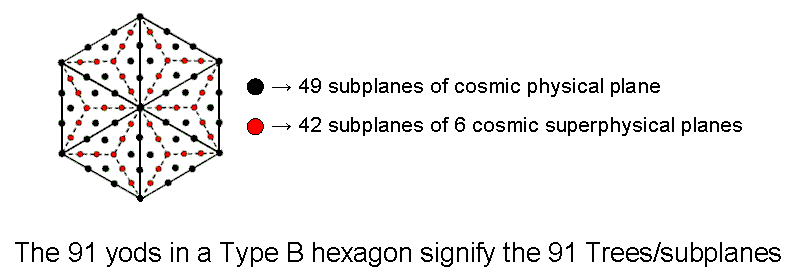
The Type B hexagon has 78 hexagonal yods, where

is the dimension of E₆, the rank-6 exceptional subgroup of the superstring Lie group E₈ (see here). Two enfolded hexagons each has 76 hexagonal yods outside the root edge, so that they embody the number of YAHWEH ELOHIM.

(2) AIN is the Kabbalistic name of the Absolute, or first of the three "hidden veils of splendour" that precede Kether. Its number value 61 is the ratio

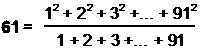
Divided into tetractyses, a Type A decagon contains 61 yods. As the geometrical symbol of the number 10, this polygon is uniquely linked to the CTOL parameter 91.

(3) The hexagon contains 73 internal yods, so it embodies the number of Chokmah.

(4) Sum of first 91 integers = 4186 = 26×161, where 161 is the number of SLs in the 26‑tree counterpart of the 26-dimensional space-time of bosonic strings. We see that the 26-tree encodes CTOL because, if the number of YAHWEH is assigned to each SL in the section of CTOL prescribed by this number, the sum of these integers is the 91st triangular number — a remarkable property of this section of CTOL. Another way in which YAHWEH is linked to the number 91 is the fact that 91 = 26 + 65, where 65 is the number of the Divine Name ADONAI substituted by Jews for Tetragrammaton (YHVH) during reading of their scriptures.

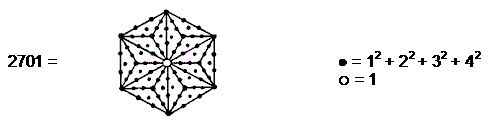
Assigning the integers 1-91 to the yods of the hexagon, the sum of the 73 interior integers 1-73 = 73×37 = 2701. This number has the hexagonal representation:

Sum of boundary integers 74-91 = 1485

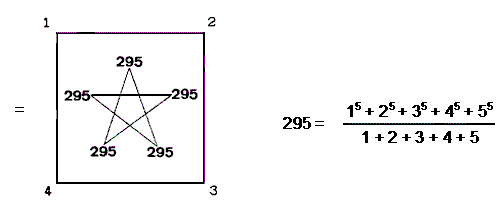
(5) Sum of squares of first 91 integers = 255346 = 26×161×61. Sum of squares of internal integers = 132349 = 73×49×37.

TYPE A + TYPE B HEXAGONS
Two separate Type A and Type B hexagons have 128 yods, where 128 is the sum of the first four Godname numbers:

128 = 21 + 26 + 50 + 31.

Joined together, they have 124 yods, where

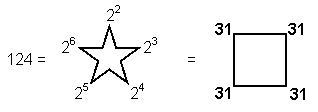
and 31 is the number of EL, the Godname of Chesed, which is the fourth Sephirah. There are 120 yods in the two joined hexagons outside their root edge, where 120 = 2² + 4² + 6² + 8² = 11² − 1

This is also the number of yods on the boundaries of the seven enfolded polygons making up each half of the inner Tree of Life (see here).

The way in which the two joined hexagons with 2nd-order tetractyses as sectors embody the superstring structural parameter 840 is discussed in #17 at Wonders of sacred geometry/Superstrings. The way in which the Type C hexagon embodies the average number of geometrical elements surrounding the centre of the Platonic solids when their vertices and the centres of their faces are joined to their centres is discussed at the end of #19 in that section. How the two joined, Type C hexagons embody the dimension 496 of E₈×E₈, one of the two symmetry groups describing superstring forces, is analyzed there in #16.

Home