| << Previous 1... 5 6 [7] 8 9 ...40 Next >> |
#7 The holistic parameter 240 in the 1-tree, inner Tree of Life & Sri
Yantra

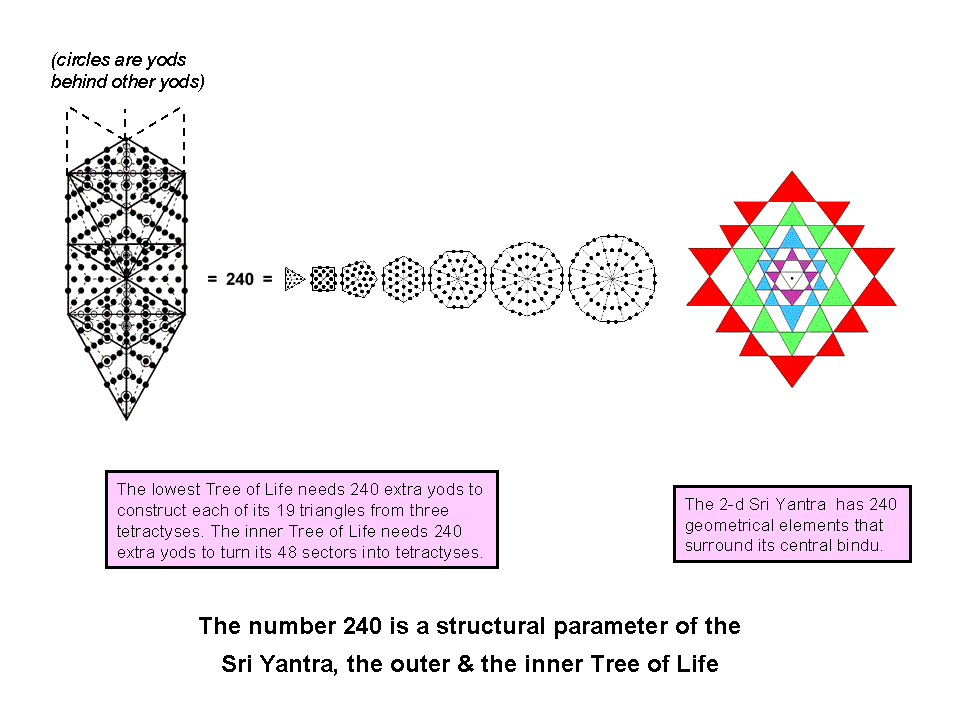
The 1-tree is composed of 19 triangles. with (19×3=57) sectors. Turning each sector into a tetractys generates a 1-tree composed of 251 yods,* i.e., 240 new yods in addition to the ten Sephiroth and Daath located at the corners of the 19 triangles.
The counterpart of this in the inner form of the Tree of Life is the 240 hexagonal yods added by the conversion into tetractyses of the 48 sectors of the seven regular polygons.
The number 240 is embodied in the geometry of the 2-dimensional Sri Yantra as the 240 corners, sides & triangles that surround its centre (for proof, see page 8 in Article 35 (WEB, PDF)). As will be proved in the section Superstrings as sacred geometry, this number is embodied in different examples of sacred geometry because it denotes the 240 roots of E8, the rank-8, exceptional Lie group that governs the unbroken symmetry of the unified force between E8×E8′ heterotic superstrings of ordinary matter (these are a singlet state of the second group E8′).
The number 251 is the sum of the squares of 1 and the numbers of corners of the first six regular polygons making up the inner form of the Tree of Life:
251 = 12 + 32 + 42 + 52 + 62 + 82 + 102.
As 12 + 32 = 10, the number of geometrical elements in the 2-d Sri Yantra (including its central bindu) is
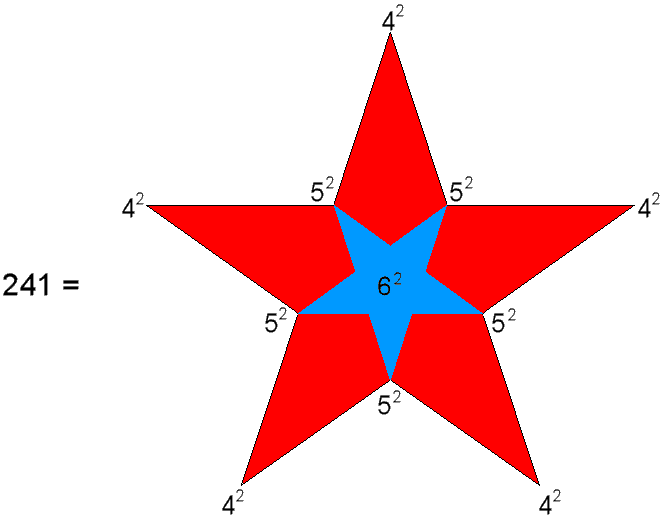
241 = 251− 10 = 42 + 52 + 62 + 82 + 102.
As 8 = 2×4 and 10 = 2×5, 241 = (1+22)(42+52) + 62 = 5(42+52) + 62. The number 241 can therefore be represented by a pentagramic array of 42 and 52 with 62 at its centre:
* Proof: The 19 Type A triangles making up the 1-tree have 11 corners and 25 sides. Two hexagonal yods lie on each side. The number of yods lining the 25 sides = 11 + 25×2 = 61. There are 10 yods inside each Type A triangle. The number of yods in the 1-tree with Type A triangles = 61 + 19×10 = 251.
| << Previous 1... 5 6 [7] 8 9 ...40 Next >> |