#23 Correspondence between the five Platonic solids and the inner Tree of Life 

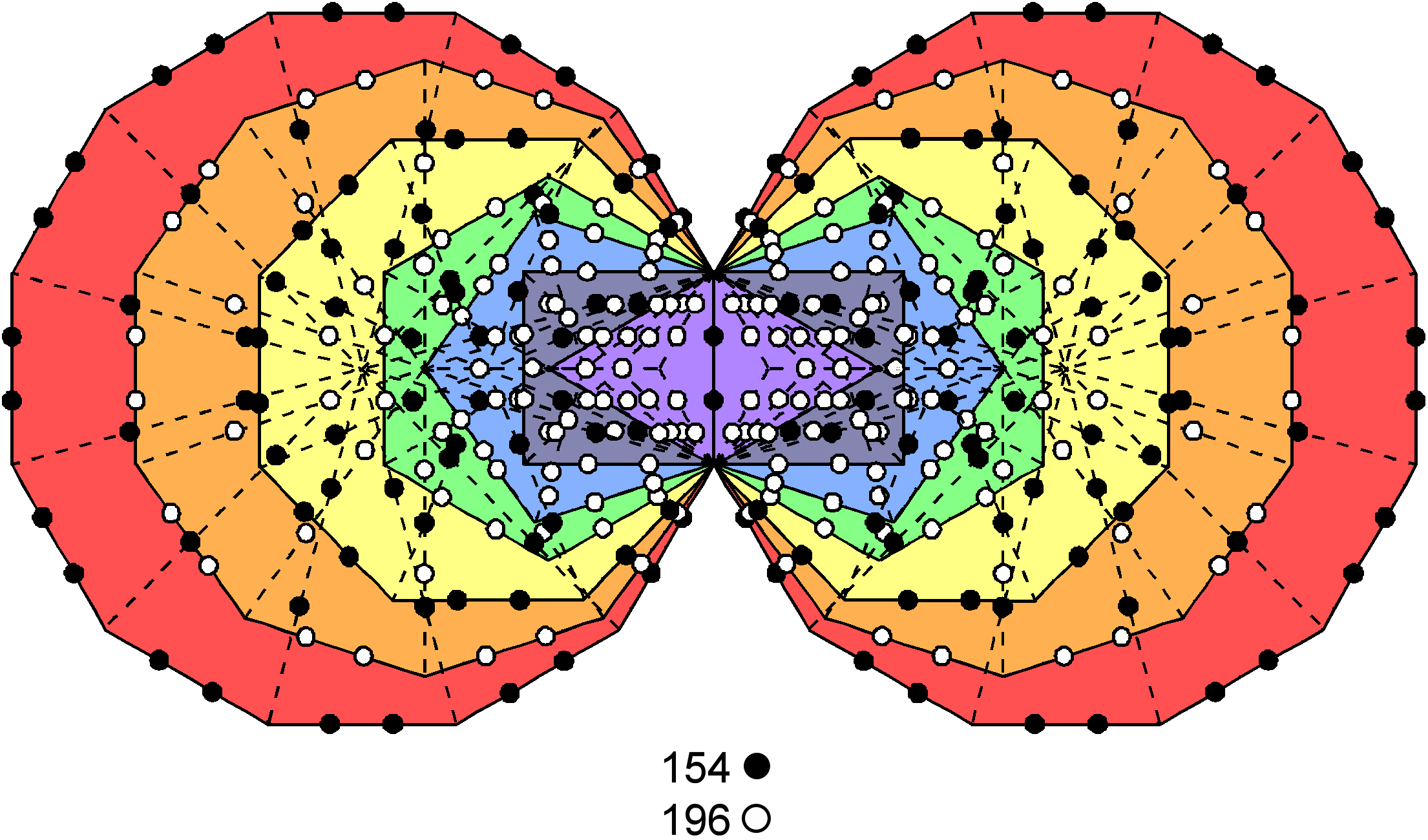
The table on page 16 of Sacred geometry/Platonic solids indicates that the 50 faces of the five Platonic solids have 820 yods and that their interiors have 1000 yods surrounding their centres when all interior triangles are Type B. The number of yods in their faces other than vertices = 820 – 50 = 770, i.e., 154 on average. As four hexagonal yods lie on each axis, the number of internal yods surrounding the 20 hexagonal yods on their axes = 1000 – 20 = 980, i.e., 196 on average. The average number of yods other than vertices surrounding their axes = 154 + 196 = 350. This number is a defining parameter of holistic systems, being, for example, 1. the sum of the 20 integers of the Tetrahedral Lambda, 2. the number of corners intrinsic to each of the two sets of 70 polygons that are enfolded in 10 overlapping Trees of Life and 3. the number of hexagonal yods lining the 94 tetractyses in the (7+7) enfolded polygons of the inner Tree of Life (see here). Let us now examine the lattermost case in more detail.

The numbers of hexagonal yods outside the root edge that line tetractyses in the seven enfolded types of polygons are tabulated below:

The octagon & dodecagon have 76 hexagonal yods outside the root edge lining 20 tetractyses and the triangle, square, pentagon, hexagon & decagon have 98 hexagonal yods outside the root edge that line 27 tetractyses. Including the two hexagonal yods in the root edge, the two sets of octagons & dodecagons have (2 + 2×76 = 154) hexagonal yods (denoted by black yods in the diagram), leaving the two sets of triangles, squares, pentagons, hexagons & decagons with (350–154=196) hexagonal yods (denoted by white yods). The former number is the average number of yods in the faces of the five Platonic solids surrounding their axes and the latter is the average number of yods inside them surrounding their axes. Even if it were coincidence that the average number of yods other than vertices surrounding the axes of the five Platonic solids happens to be the number of hexagonal yods on edges of tetractyses in the inner Tree of Life, what is the likelihood that two combinations of polygons also exist by chance whose yod populations happen to be the numbers of yods in the faces and in the interiors of these solids? It is obviously very implausible that both circumstances would occur fortuitously.

 

<< Previous    1...   21  22  [23]  24  25  ...81    Next >>

Home