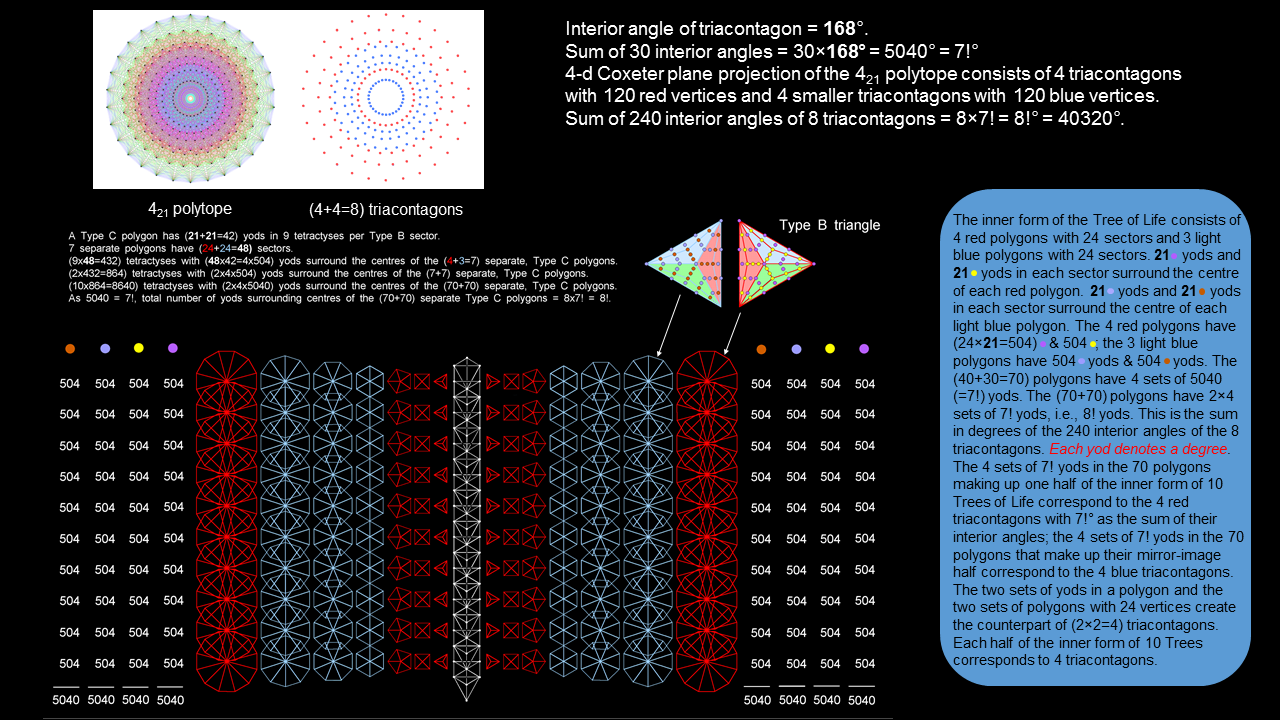
The yod population of the (70+70) separate Type C polygons in the inner form of 10 Trees of Life matches in number and pattern the sum of the interior angles of the 8 triacontagons formed in the E8 Coxeter plane by the 421 polytope.
| << Previous 1 2 [3] 4 5 ...17 Next >> |
3. The sum of the interior angles of the 8 triacontagons is the yod population of the inner form of 10 Trees of Life with Type C polygons
 |
|
The yod population of the (70+70) separate Type C polygons in the inner form of 10 Trees of Life matches in number and pattern the sum of the interior angles of the 8 triacontagons formed in the E8 Coxeter plane by the 421 polytope. |
Surrounding the centre of a Type C n-gon are 42n yods. They can be divided into two sets of 21n yods. The 7 separate polygons making up each half of the inner Tree of Life consist of the triangle, square, pentagon & dodecagon with 24 corners and the hexagon, octagon & decagon with 24 corners. Hence the 7 polygons contain four sets of (21×24=504) yods. Similarly for the mirror-image set of 7 Type C polygons. The (7+7) Type C polygons contain (4+4=8) sets of 504 yods. The (70+70) Type C polygons generated by 10 overlapping Trees of Life contain (4+4) sets of 5040 yods. Compare this with the fact that the sum of the interior angles of a triacontagon is 5040, so that the (4+4) triacontagons have (120+120=240) interior angles of 168° that add up to (4+4)×5040. Both in magnitude and in pattern, this is the same as the yod population of the inner form of 10 Trees. Each yod denotes a degree. Each half of this inner form corresponds to the 4 triacontagons in the Coxeter projection of a 600-cell. This is additional evidence for the Tree of Life nature of the 421 polytope whose 4-dimensional projection is a compound of two 600-cells.
| << Previous 1 2 [3] 4 5 ...17 Next >> |