How the Tetrad & tetractys generate the dimension 248 of the rank-8, exceptional Lie group E₈

We found on page 16 that, when its 595 triangles are tetractyses, the 49-tree mapping the cosmic physical plane contains 2480 yods. According to E₈×E₈ heterotic superstring theory, the unified force between superstrings of ordinary matter is transmitted by the 248 gauge fields of E₈, the rank-8, exceptional Lie group. These gauge fields exist in 10-dimensional space-time, so that they have 2480 space-time components. Each component can be thought of being symbolised by a yod in the 49-tree constructed from tetractyses. This establishes a remarkable conjunction of group theory, superstring physics, the mystical tradition of Kabbalah and the teaching of Theosophy that the cosmic physical plane consists of seven planes, each with seven subplanes. For the lattermost is mapped by the 49-tree, namely, the lowest 49 of the 91 overlapping Trees of Life making up the Cosmic Tree of Life (CTOL). This shows how EL CHAI, the Godname of Yesod with number value 49 (see here) prescribes the dimension 248 of E₈.

Consider the tetractys arrays t_n & T_n of the integers 1, 2, 3 & 4 raised to the power n (see diagram). The table lists their values for n = 0, 1, 2, 3 & 4. Since T₀ = t₀ = 10 and T_n ≠ t_n for n = 1, 2, 3 & 4, there are nine different numbers generated by the tetractys arrays for these first five powers. Writing down the two types of arrays in order of increasing n, their sum is:

2480 = t₀ (or T₀) + (t₁ + t₂) + (t₃ + t₄ + T₁ + T₂ + T₃ + T₄)

= 10 + 70 + 2400 = 80 + 2400.

Together with zero, the four Pythagorean integers 1, 2, 3 & 4 have the amazing property of generating both the root composition of E₈ and the population of the 49-tree. t₀ or T₀ (= 10) denotes the 10 yods added when the Tree of Life with 70 yods becomes the 1-tree, (t₀ + t₁) (= 30) is the number of yods in its Lower Face (the kite-shaped quadrilateral with Tiphareth, Netzach, Hod & Malkuth at its corners) and t₂ (= 50) is the number of yods in the rest of the 1-tree outside the Lower Face. Hence, (t₀ + t₁ + t₂) (= 80) is the yod population of the 1-tree (see here) and (t₃ + t₄ + T₁ + T₂ + T₃ + T₄) (= 2400) is the population of the 48 Trees of the 49-tree above the 1-tree. The 80 yods denote the 80 space-time components of the eight gauge fields associated with the eight simple roots of E₈ and the 2400 yods denote the 2400 space-time components of its 240 roots. In other words, the distinction between the lowest Tree of Life and the 48 Trees in the 49-tree above it corresponds to the difference between the so-called eight "zero roots" and the 240 "non-zero roots" of E₈, as well to the difference between the first three tetractys arrays (t₀, t₁, t₂) and the last six (t₃, t₄, T₁, T₂, T₃, T₄). As t₀ is identical to T₀, it makes no difference to the sum (2480) of the nine tetractyses which one of these two tetractyses should be included in them. However, given (see here) that the yod population of the Tree of Life = 70 = t₁ + t₂, the more natural choice for the difference of 10 yods between the Tree of Life and the 1-tree is t₀ because, then, the nine tetractyses divide into the first five of one type: t₀, t₁, t₂, t₃ & t₄, and the last four of the other type: T₁, T₂, T₃ & T₄, whereas choosing T₀ would mix the two types in the three tetractyses adding to 80.

Embodied, therefore, in the Tree of Life map of the cosmic physical plane is the number of space-time components of the 248 gauge fields of E₈. Here is how superstring physics with unbroken E₈ symmetry is related to the mathematical description of the levels of physical and superphysical reality. If the sceptic wants to argue that the 49-tree embodies the number 248 by coincidence, then he or she has to accept that it must also be just a matter of chance that the nine possible tetractys arrays of the powers of 1, 2, 3 & 4 add up to 2480 and that the values 10, 20 & 50 of the first three tetractyses are, respectively, the 10 yod difference between the Tree of Life and the 1-tree, the 20 yods in the tetrahedron of the 1-tree and the 50 remaining yods of the 1-tree (the number of yods in n Trees of Life = 50n + 20 and the number of yods in the n-tree = 50n +30, where 20 = t₁, 30 = t₀ + t₁ and 50 = t₂). That all these mathematical counterparts could exist by coincidence is highly implausible. A more reasonable view is that we are encountering here yet another remarkable example of the harmony of Pythagorean geometry and number in the context of sacred geometry and its manifestation in group theory in the superstring gauge symmetry group E₈. The significance of the 49-tree is that it maps the cosmic physical plane, so that it corresponds on a cosmic level to the last Sephirah of Construction, namely, Malkuth. Hence, it should not come as a surprise that this section of CTOL should embody the number of gauge fields that transmit the unified force between superstrings of ordinary matter making up the physical universe. We say "ordinary" because, according to E₈×E₈ heterotic superstring theory, this type of matter is a singlet state of the second E₈ group, which is the invariance group for the interactions between shadow matter superstrings mediated by another set of 248 spin-1 gauge fields with 2480 space-time components. The total number of such components of the 496 gauge fields is 4960. This number is not, of course, represented in the yod population of CTOL, which has 4570 yods, because its context is the physical universe, which means that it should be expected to be embodied in only that section of CTOL that bears a correspondence to Malkuth, the last Sephirah — namely, the 49-tree. However, it is readily shown* that the number of yods in n overlapping Trees of Life that are either on the Pillar of Equilibrium or directly in line with it = 10n + 6, so that 49 overlapping Trees have 496 such yods, where 496 is the number value of Malkuth:

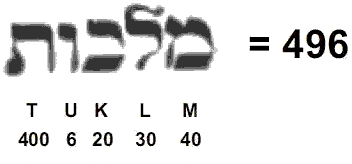
The 49-tree therefore embodies the dimension 248 of E₈ and 49 overlapping Trees embody the dimension 496 of E₈×E₈.** The appearance of these two group-theoretical numbers characterising one of the superstring theories in the Tree of Life mapping of the cosmic physical plane is very remarkable and cannot, plausibly, be due to coincidence. Instead, it further demonstrates the Pythagorean geometrical basis of superstring theory itself. It also illustrates the hermetic axiom "As above, so below" because, as the representation of the cosmic physical plane, the 49-tree is the counterpart of the 7-tree mapping the physical plane, that is, the 10-dimensional space-time of superstrings.

E₈ embodied in the 5 Platonic solids
Discussed here is the geometrical composition of the five Platonic solids with their faces divided into their sectors and with the sides of the latter regarded as also sides of internal, Type A triangles with the centre of the polyhedron as one of their corners. It is found that, excluding their vertices, 2480 points, lines & basic triangles surround the axes of the five regular polyhedra passing through their centre and any two vertices diametrically opposite it. Given the 50 points in 3-dimensional space where their vertices are located, 2480 more geometrical elements surrounding their axes are needed to construct their faces and interiors from triangles. Compare this with the fact that the 49-tree is composed of 2480 yods when constructed from tetractyses, that is, the number of yods in 248 tetractyses. We find that the same parameter is found in different holistic systems! Again, this should come as no surprise, for they are different representations of the same archetypal Whole. Adding the 40 vertices of the five Platonic solids that surround their axes makes a total of 2520 geometrical elements. This is the number of yods in 50 overlapping Trees of Life. ELOHIM, the Godname of Binah with number value 50, prescribes two sacred geometrical systems embodying the same number. We may think of the 40 extra yods above the 49-tree in the 50th Tree as corresponding to the 40 skeletal points that surround the axes of the five Platonic solids as vertices, with the 2480 yods in the 49-tree corresponding to the 2480 remaining geometrical elements that surround their axes. Remarkably, Binah of the 50th Tree of Life determined by the Godname of this Sephirah is the 248th SL from the top of CTOL Once again, the dimension 248 of the superstring gauge symmetry group E₈ appears in the properties of sacred geometries, prescribed by ELOHIM. Can this, too, be merely a matter of chance, as the sceptic has to argue in order to be consistent with his denial that sacred geometries possess an analogous design that is of divine origin? Of course not!

* Proof: The 1-tree (shown here) has 10 yods either on or aligned with the central Pillar of Equilibrium inside the lower kite shape with Tiphareth, Netzach, Hod & Malkuth at its corners. The upper kite shape in the 1-tree with Kether, Chokmah, Binah & Tiphareth at its corners also has 10 such yods above its lowest point. The n-tree has (n+1) kites joined end-to-end, each with 10 yods either on this pillar or aligned with it. The number of yods either on or aligned with the central pillar of the n-tree ≡ N(n) = 10n +10. Comparing #39 & #40, the upper kite in the Tree of Life has 4 fewer yods of this type than the upper kite in the 1-tree. The number of yods either on or aligned with the central pillar of n overlapping Trees of Life ≡ Ň(n) = 10n + 10 − 4 = 10n + 6. Hence, 49 overlapping Trees have (Ň(49) = 496) yods that are either on the Pillar of Equilibrium or aligned with it in the line of sight.

** 49 overlapping Trees also embody in their geometry the superstring structural parameter 1680. The (12n+4) triangles in n overlapping Trees have (6n+4) corners and (16n+6) sides, i.e., (34n+14) geometrical elements. Therefore, 49 overlapping Trees are composed of (34×49 + 14 = 1680) geometrical elements. The Tree of Life map of the cosmic physical plane embodies both the structural parameter 1680 and the dynamical parameters 2480 & 496 of E₈×E₈ heterotic superstrings, as manifested in the UPA. The sceptic should ask himself: what is the likelihood of such a triple conjunction of numbers relevant to superstring theory occurring by chance? Why should the first number, derived by C.W. Leadbeater by remote viewing UPAs and counting the 1680 turns in each of its whorls, turn up in the same context alongside two numbers connected with superstring theory if the UPA was NOT a real superstring but merely the product of his imagination?! Here is convincing evidence that the UPA is, indeed, a superstring, as interpreted by the author in his book ESP of Quarks & Superstrings — in particular, the E₈×E₈ heterotic superstring.

 

<< Previous    1...   36  37  [38]  39  40  ...50    Next >>

Home