
| << Previous 1... 6 7 8 [9] 10 Next >> |
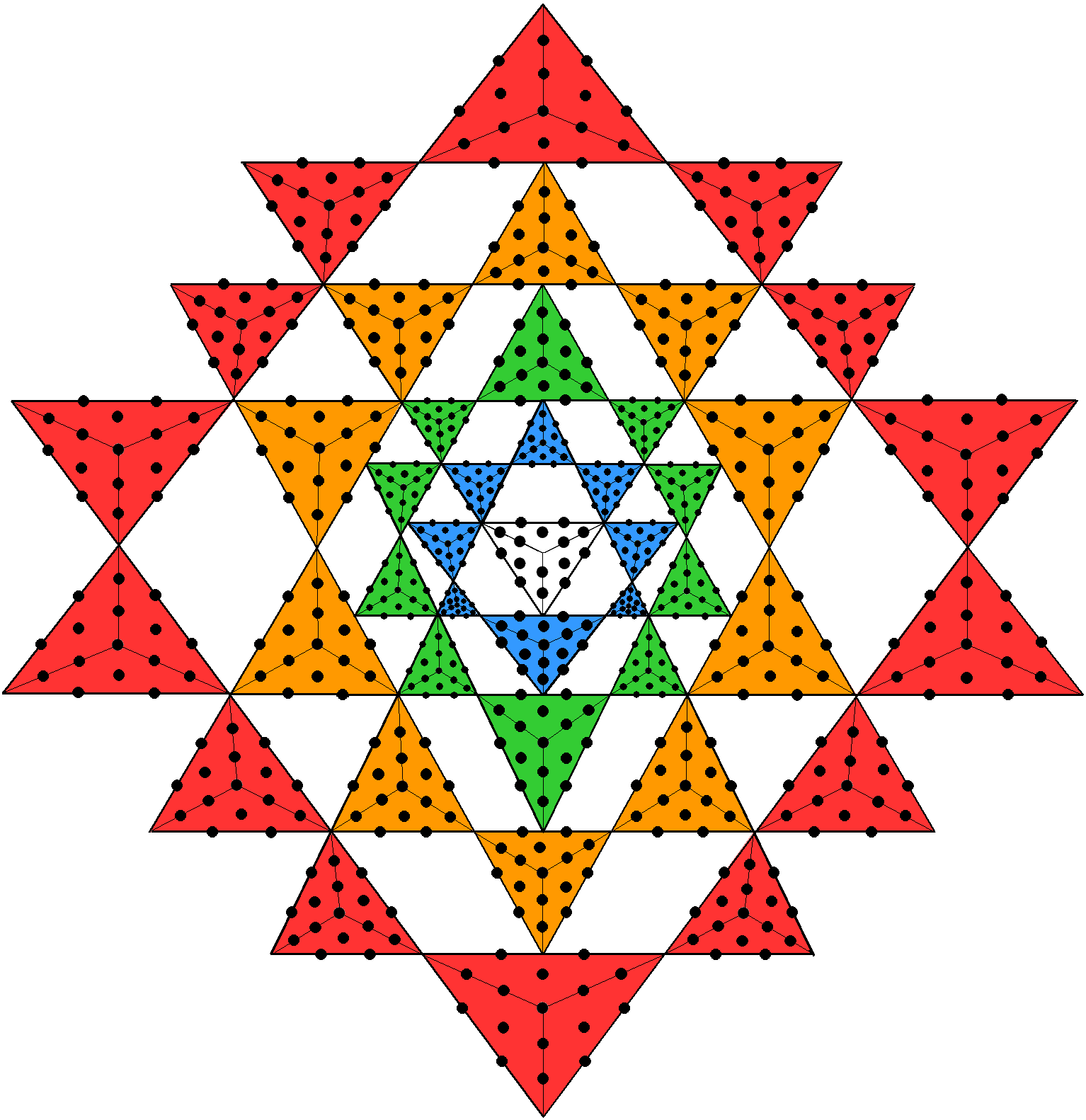
The Sri Yantra with Type B triangles embodies the number of edges of the 421 polytope whose 240 vertices determine the 240 root vectors of E8

A Type A triangle contains 19 yods. Of these, three are corners, so that 16 more yods are needed to turn a simple triangle into a Type A triangle whose sectors are tetractyses. The 42 triangles surrounding the centre of the 2-dimensional Sri Yantra contain (42×16=672) yods other than their 68 corners when they are Type A triangles. In other words, 672 more yods are needed to construct their (3×42=126) sectors from tetractyses. When each yod is weighted with the Decad, the Sri Yantra embodies the number 6720. This is the number of edges in the 421 polytope, the 8-dimensional, semi-regular polytope whose 240 vertices define the 240 root vectors of the Lie group E8. (see here). The Sri Yantra therefore embodies the very number (apart from the Pythagorean factor of 10) that is the number of edges of the 421 polytope associated with the forces between E8×E8 heterotic superstrings. For more discussion of the amazing connection between this sacred geometry and the 421 polytope, see here.
Of the 672 yods in the 42 Type A triangles that are not their corners, 42 yods are still corners of tetractyses, leaving 630 hexagonal yods. The number 630 is the number value of Seraphim , the Order of Angels that is assigned to Geburah.
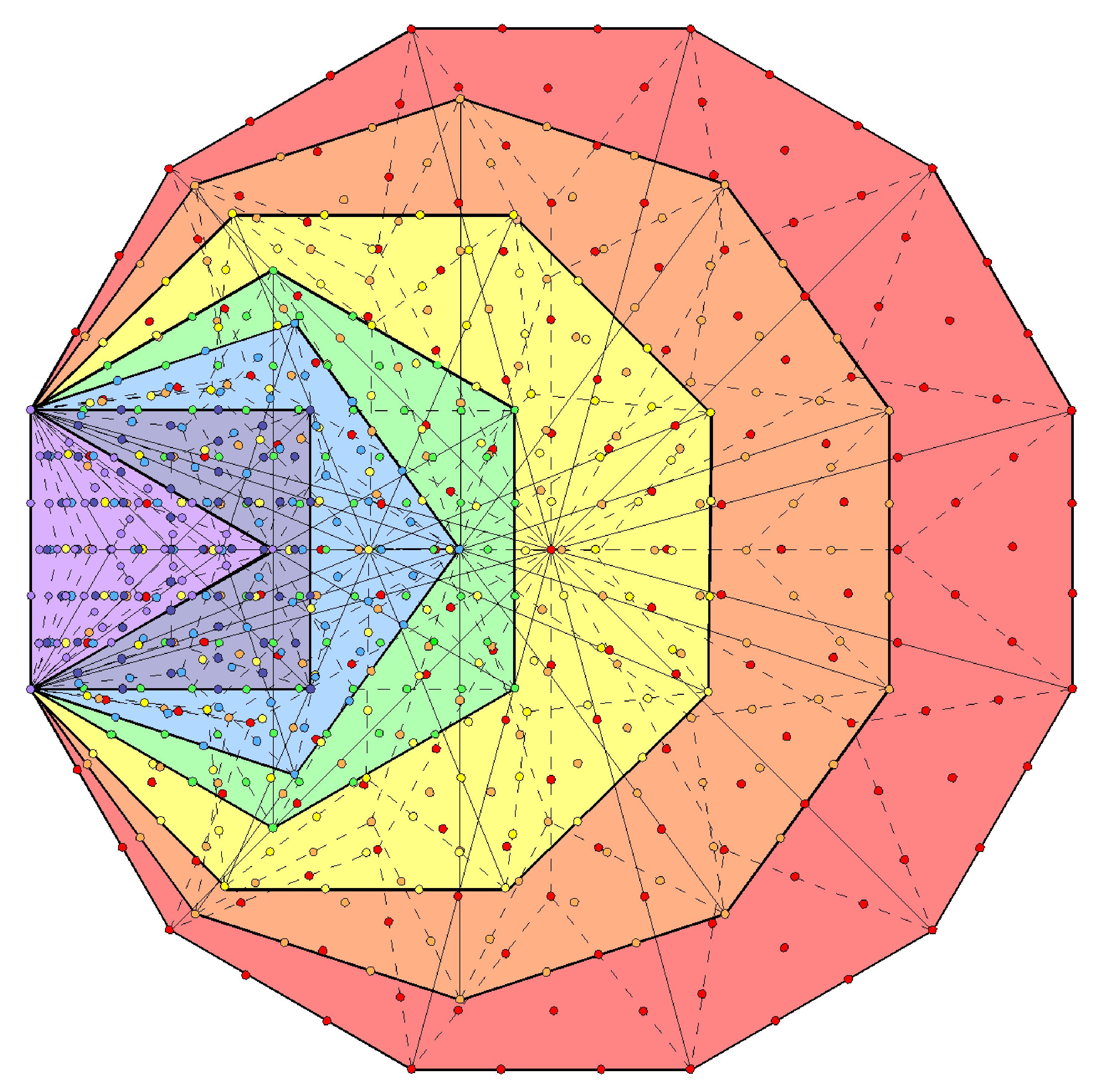
Although traditionally regarded as a triangle, the downward-pointing, three-sided figure at the centre of the 2-dimensional Sri Yantra is not, from a strict, mathematical point of view, a triangular area that can be turned into a Type A triangle because the bindu as a separate point symbolising the Absolute is assigned to its centre. As the source of all levels of Creation, the Absolute (Parabrahman) stands, so to speak, 'outside' it always, so that the bindu cannot be counted with other yods or included with the geometry of the Sri Yantra that represents these levels. For this reason, it is illegitimate to treat this central, three-sided figure as a true triangle on the same par as the 42 triangles that surround it. It is, however, legitimate, when the Sri Yantra is a 3-dimensional stack of four sheets of Type A triangles, with the central bindu* hovering above the central (white) Type A triangle. In this case, 15 yods in the latter other than corners surround its centre. The number of yods other than corners of the 43 Type A triangles that surround the central axis passing through the bindu and the centre of the central triangle = 15 + 672 = 687. Remarkably, this is the number of yods in the seven enfolded polygons of the inner Tree of Life when their 47 sectors are Type A triangles**:
 |
 |
|
The 47 sectors of the 7 enfolded Type B polygons contain 687 yods. |
The centre of the 3-d Sri Yantra is surrounded by 687 yods in the 43 Type A triangles that are not their corners. |
Moreover, seven yods lie on the two internal vertical sides of sectors in the hexagon that are shared with the triangles in the outer Tree of Life, whilst two yods on the root edge are associated with each set of seven enfolded polygons. This means that 15 of the 687 yods either lie on the root edge, are shared with the outer Tree of Life or are centres of polygons, leaving 672 yods surrounding these centres that are intrinsic to the inner Tree of Life. These 15 yods correspond to the 15 hexagonal yods making up the central triangle in the Sri Yantra that symbolises the triple Godhead of Shiva, Brahma & Vishnu:
|
7 enfolded, Type B polygons |
3-d Sri Yantra |
|
| Top, centre & bottom of hexagon; |
↔ |
3 hexagonal yods at centres of 3 tetractyses in central triangle; |
| Pair of yods on root edge + 2 pairs of hexagonal yods in hexagon shared with outer Tree of Life; |
↔ |
3 pairs of hexagonal yods on sides of central triangle; |
| 6 centres of polygons other than hexagon; |
↔ |
6 hexagonal yods on sides of tetractyses inside central triangle; |
| 672 yods outside root edge unshared with outer Tree and surrounding centres of polygons; |
↔ |
672 yods not corners of 42 Type A triangles surround central triangle. |
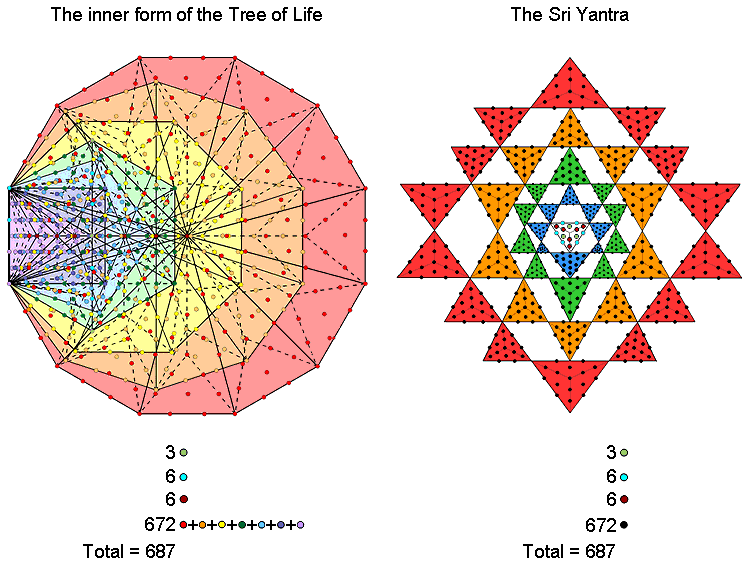
Correspondence between the inner Tree of Life and the 3-dimensional Sri Yantra.
The 672 intrinsic yods surrounding centres of polygons correspond to the 672 extra yods needed to turn the 42 triangles in the Sri Yantra into Type A triangles. What more convincing evidence of the equivalence of two sacred geometries could be offered? It is ridiculous to ascribe this matching to chance because consistency then demands that all other examples of correspondences between the Sri Yantra and sacred geometries discussed elsewhere in this website should, likewise, be dismissed as coincidental — the probability of which is extremely small. Trying to explain all these correspondences as the result of chance requires believing in the possibility of miracles. A more plausible view is that the two yod populations and their 15:672 division are the same for the simple reason that they are isomorphic, sacred geometrical representations of the same object — namely, the 421 polytope, whose 240 vertices determine the symmetry group E8 governing the E8×E8 heterotic superstring forces that build the universe. The Sri Yantra is an alternative representation of the inner form of the Tree of Life, containing exactly the same parameters, such as 672 and 336, that characterise the universal blueprint found in sacred geometries. The former version is composed of triangles; the latter is made up of seven types of regular polygons. As explained in detail in 4-d sacred geometries, the 421 polytope is the polytopic version of this blueprint, just as the first four Platonic solids are its regular, polyhedral version, for they contain 672 yods when constructed from tetractyses (see #15 in 4-d sacred geometries).
As
153 − 15 = 3360 = 672×5,
672 = (153−15)/5
and
687 = 672 + 15 = (153−15)/5 + 15.
This shows how YAH (יה), the shortened Godname of Chokmah with number value 15, prescribes in a purely arithmetic way the yod populations of the inner Tree of Life and the 3-dimensional Sri Yantra constructed from Type A triangles. The complete Godname YAHWEH (יהוה) with number value 26 does the same because 672 = 262 − 4, so that 687 = 672 + 15 = 262 + 11. As the seven enfolded polygons have four yods on their root edge and seven centres, the number of yods outside the root edge that surround the centres of the seven enfolded Type B polygons = 262. The number of yods outside the root edge needed to shape the inner Tree of Life, starting from the centres of its seven polygons, is simply the square of the number value 26 of YAHWEH, the ancient Hebrew name for the creative aspect of God.
As
687 = 262 + 11 = (153−15)/5 + 15 = 3×152 − 3 + 15 = 3×152 +12,
262 = 1 + 3×152.
This relates the number values of the partial (15) and complete (26) Godname of Chokmah. As 3×15 = 45 and 1 + 45 = 46, 262 has the following representation in terms of the 46 yods of a Type B triangle:
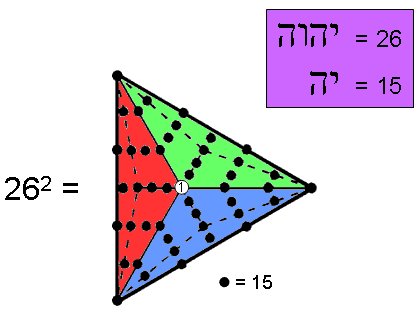
Weighted with the number 15 of YAH, the 45 yods surrounding the central yod symbolising 1 generate the number of yods outside the root edge that surround the centres of the seven enfolded Type B polygons. This is how the simplest, geometrical shape — the triangle — embodies when it is Type B the number of yods needed to create the nested set of regular, Type B polygons that make up the inner form of the Tree of Life. The Type B triangle has 46 yods. 46 is the human diploid number (number of types of chromosomes in the cell of the human body). The sum of the first 46 integers is 1081, which is the number of Tiphareth ("Beauty"), the Sephirah at the centre of the Tree of Life.
* The bindu is omitted from the diagram to avoid creating the false impression that it is meant to be included in the yod population with all the other yods.
** For proof, see #72 at Wonders of correspondences.
| << Previous 1... 6 7 8 [9] 10 Next >> |