Godname

 Mathematical prescription

The sum of the first 21 binary coefficients other than 1 = 240:

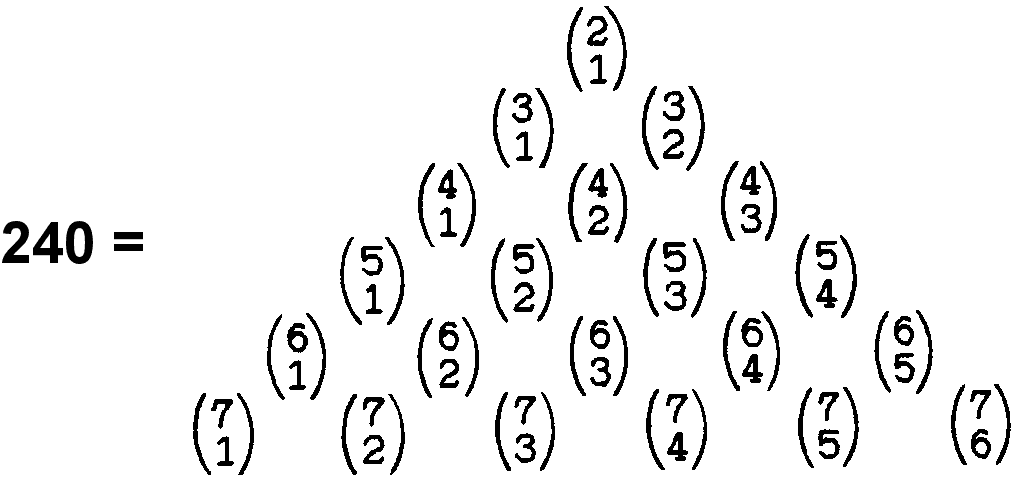
This is the number of vertices of the 4₂₁ polytope.

The sum of the first 15 even integers = 2 + 4 + 6 + 8 + .. + 30 = 240. This is the number of vertices of the 4₂₁ polytope. The number of vertices in each half of the 4₂₁ polytope = 120 = 15th triangular number.

As 15² − 1 = 224, 3360 = 15×224 and 6720 = 2×3360 = 2×15×(15²−1). This is the number of edges of the 4₂₁ polytope. The number of edges in each half of the polytope = 3360 = 15×(15²−1) = 15³ − 15. This is the number of dots outside one edge in a cubic array of dots with 15 dots spaced equally along each edge.

6720 = 4×1680 = 10×4×168 = 10×2²×(13²−1) = 10×(26²−2²).

26 of the 1370 yods in the inner Tree of Life with Type B polygons are either centres of polygons or yods shared with the outer Tree of Life. Surrounding these centres are (1370−26=1344=2×672) intrinsic yods. Surrounding the centres of the (70+70) polygons enfolded in 10 Trees of Life are 240 yods that are either centres or yods shared with these Trees and 2×6720 intrinsic yods. The former correspond to the 240 vertices of the 4₂₁ polytope and the latter correspond to the 2×6720 hexagonal yods on its 6720 edges. YAHWEH differentiates those yods that correspond to the 240 vertices of the 4₂₁ polytope from those that denote its edges.

The 6720 edges of the 4₂₁ polytope are arithmetically related to the 16800 turns of the 10 helical whorls of the UPA and to the 2480 space-time components of the 248 10-dimensional gauge fields of the rank-8, exceptional Lie group E₈ by

6720 = 16800×2480/(2²+3²+4²+...+26²).

(for proof, see bottom of #12).

The number of faces of the 4₂₁ polytope = 60480 = 9×6720. The number of edges & faces = 6720 + 9×6720 = 10×6720 = 67200 = 50×1344. In other words, it is the number of yods intrinsic to the 700 regular polygons enfolded in 50 Trees that surround their centres. ELOHIM, the Godname of Binah with number value 50, prescribes the number of shape-forming edges & faces of the 4₂₁ polytope. Also:

6720 = 10×(26² − 2²) = 10×(5+7+9+...+51),

where 51 is the 50th integer after 1. ELOHIM prescribes the number of edges in the 4₂₁ polytope.

The number of corners, sides & triangles in the faces and interior of the 4₂₁ polytope = 74400 = 31×10×240 (see the first table in #12). The 31st prime number is 127. This is the number of triangles in the 10-tree constructed from Type A triangles. Its inner form contains 13680 yods, which is the number of yods lining the edges of the 4₂₁ polytope when its faces are tetractyses: 240 + 2×6720 = 13680.

The number of yods lining the edges of the 4₂₁ polytope when its faces are tetractyses = 240 + 2×6720 = 13680 = 1368×10. As 37² − 1 = 3 + 5 + 7 +... + 73 = 1368, the number of boundary yods shaping the 4₂₁ polytope is the number of yods in 1368 tetractyses, where 1368 is the sum of the first 36 odd integers after 1. ELOHA prescribes the boundary of the 4₂₁ polytope. As the last of these odd integers = 73 = 21st prime number, this is how EHYEH prescribes the number of yods lining the edges of the 4₂₁ polytope_.

The compound of two 600-cells has 240 vertices that are the 4-dimensional projection of the 240 vertices of the 4₂₁ polytope. The two 600-cells have (1200+1200=2400) triangular faces and (720+720=1440) internal triangles, making a total of 3840 (=384×10) triangles. 384 is the 383rd integer after 1, where 383 is the 76th prime number.

6720 = 16800×2480/(2²+3²+4²+...+26²).

As 168 = 13² − 1,

16800 = 168×10² = (13² − 1)10² = 130² −10² = (2×65)² − (2×5)²

= 4(65² − 5²).

65² = 1 + 3 + 5 + 7 + 9... + 129

and

5² = 1 + 3 + 5 + 7 + 9.

Therefore,

16800 = 4(11+13+15+... +129).

and

6720 = (11+13+15+...+129)×4×2480/(2²+3²+4²+...+26²).

154×240 hexagonal yods are in the 30240 faces in each half of the 4₂₁ polytope constructed from tetractyses, where 154 is the 153rd integer after 1 (see commentary on the second table in #12).

An octagon whose sectors are tetractyses contains 49 yods. Surrounding the centres of two separate Type C octagons are 672 yods. Weighted with the Decad, they generate the number 6720 (see #19).

The 10-tree has 65 Sephirothic levels (see #2 in Wonders of superstrings). The 13680 yods in its inner form correspond to the 13680 yods lining the edges of the 4₂₁ polytope when its faces are tetractyses.

The number of corners, sides & triangles in the faces and interior of each half of the 4₂₁ polytope = 74400/2 = 37200 = 155×240.