| << Previous 1 [2] 3 4 5 ...56 Next >> |
#2 The Tree of Life basis of the 248 roots of E8 & the 1680 turns of a whorl of the UPA/subquark superstring

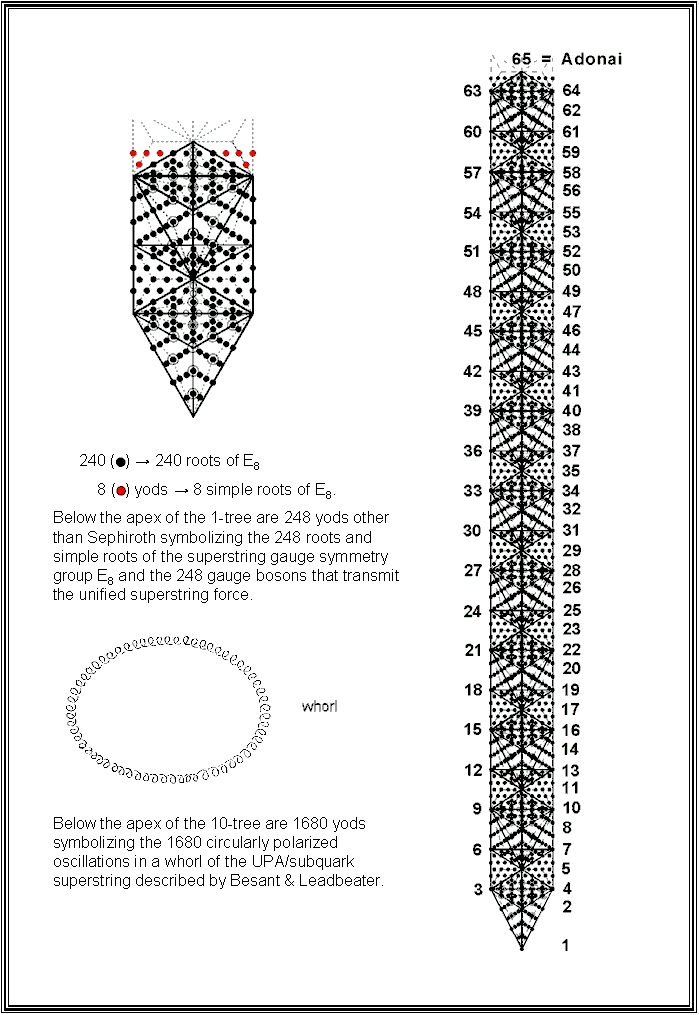
When its 19 triangles are divided into their 57 sectors and the latter then turned into tetractyses, the lowest of any set of overlapping Trees of Life has 251 yods. Eleven of these are SLs, leaving 240 black yods. There are four red yods below its top outside this Tree on either side of the central Pillar of Equilibrium. The eight red yods symbolize the eight simple roots of the Lie group E8 and the 240 black yods denote its 240 roots. 248 yods are needed to construct the lowest Tree of Life (the most Malkuth level of the Cosmic Tree of Life), starting from its apex. This demonstrates par excellence the holistic nature of this number. What this geometrical basis of the roots of E8 means is that 248 gauge fields are needed to create the physical, subatomic realization of the Tree of Life — the superstring.
The number of yods below the top of the n-tree with the sectors of its triangles turned into tetractyses is given by:
N(n) = 158n + 100.
Hence, N(10) = 1680. In other words, 1680 yods are needed to create the lowest ten Trees, starting from the mathematical point of their apex, the 65th SL. This is the remarkable way in which ADONAI with number value 65 prescribes the superstring structural parameter 1680 recorded by Charles Leadbeater when he examined the whorls of a UPA with micro-psi vision and counted their helical turns (see page 11 here). What better example could there be of how each Godname mathematically determines those aspects of the Tree of Life that are the expression of its corresponding Sephirah? For ADONAI is the Godname of Malkuth, which signifies the physical aspect of a realization of the Tree of Life blueprint. The whorls that comprise the UPA/superstring are the physical, microscopic manifestation of the 10 Sephiroth — the Malkuth level of the Tree of Life in the subatomic world. Each whorl can, therefore, be represented by 10 Trees of Life. Constructed from tetractyses, the 1680 yods below their apex symbolize the 1680 turns of each helical whorl. The number of triangles in the n-tree = 12n + 7, so that they have (36n+21) sectors, i.e., the 127 triangles in the 10-tree has 381 sectors, where 127 is the 31st prime number and 31 is the number value of EL ("God"), the Godname of Chesed. The diagram shows that four yods belonging to two tetractyses lie outside the 10-tree below its apex on either side of its central pillar. Therefore, the 1680 yods belong to (381+2+2=385) tetractyses, where
| 12 | ||||
| 22 | 32 | |||
| 385 = | 42 | 52 | 62 | |
| 72 | 82 | 92 | 102 . |
This demonstrates how the Decad determines the number of tetractyses containing 1680 yods. It also determines the number (65) of corners of the 127 primary triangles in the 10-tree because 65 is the sum of the first ten integers after 1:
| 2 | ||||
| 3 | 4 | |||
| 65 = | 5 | 6 | 7 | |
| 8 | 9 | 10 |
11 . |
Such mathematical beauty in the embodiment in the 10-tree of this superstring structural parameter cannot be dismissed as the product of chance!
Here is amazing evidence that links ostensible, paranormal observations of subatomic particles to Kabbalah. The only conventional explanation that the sceptic can resort to is coincidence. He is forced to argue that it just happens by chance that there are 248 yods below the top of the 1-tree and it is equally coincidental that there are 1680 yods below the top of the 10th Tree of Life, etc, etc, even though the first number characterises the very exceptional Lie group E8 whose symmetries refer to the E8×E8 heterotic superstring with which the author has identified the UPA remote-viewed by Besant & Leadbeater and whose helical whorls contain 1680 turns! The question is: how many miracles of chance like these can the sceptic entertain before he finally admits that his position is untenable because it requires accepting a highly improbable series of implausible coincidences? It is not as though these numbers appear through cherry-picking some aspect of the Tree of Life that happens to possess the desired property. The 1-tree and the 10-tree are not arbitrary sets of Trees. Instead, they are analogous, Kabbalistically speaking, the latter being the expanded version of the ten SLs below the top of the former. Moreover, in both cases here, the numbers refer not to what makes up different, unrelated parts of them — what would be expected if they had been generated by cherry-picking — but to the yods below their respective apices, that is to say, what makes up corresponding features of their analogous structures. It is implausible in the extreme to attribute this, too, to chance!
| << Previous 1 [2] 3 4 5 ...56 Next >> |